J. Cent. South Univ. Technol. (2011) 18: 259-265

DOI: 10.1007/s11771-011-0688-4

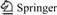
Evolution of aggregate surface texture due to tyre-polishing

CHEN Xian-hua(陈先华)¹, B. STEINAUER², WANG Da-wei(王大为)²

1. Transportation College, Southeast University, Nanjing 210096, China;

2. Institute of Road and Traffic Engineering, RWTH-Aachen University, D52074, Germany

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: Three kinds of aggregates were polished by genuine pneumatic rubber tyres. The initial states of surface texture and dynamic friction coefficient were measured and their developments in polishing process were monitored. The characterizations of height distribution and power spectral density of aggregate surface texture were estimated. The changes of micro-texture were also investigated based on a fractal filtering method with sound theoretical backgrounds of rubber friction on rough surfaces. Global height reduction and differential removal of mineral component are observed in polishing process. It is concluded that the tyre-polishing action plays the critical roles in the micro-scale texture, and the evolution of friction of aggregate is governed by the micro-texture changes due to the differential removal of mineral component.

Key words: tyre polishing; dynamic friction coefficient; aggregate surface texture; micro-texture

1 Introduction

Polishing of the surface of asphalt pavements and consequent descend of the skid resistance with time are world-wide issues in considering highway safety. Aggregates, constituting more than 90% (mass fraction) asphalt pavement materials, have a significant role in surface performance such as friction and noising. The importance of aggregate surface texture in tyre/road friction can be dated back to the research conducted by KNILL in 1960 [1]. However, it is until recent years that the changes of aggregate surface texture due to rubber tyre polishing action have been quantitatively investigated when the micrometer-level for texture measuring and new accelerated polishing machine were adopted [2-4]. The characterization of surface texture considering friction can be approached through: 1) basic analysis [3, 5-6], to estimate some geometric or statistical parameters, such as curve length of the profiles, surface area of the summit, height distribution, root mean square or higher moments, and/or angle parameter, 2) fractal analysis [7-9], using correlation function to estimate the fractal dimension, and 3) spectral analysis [10]. As most of the existing accelerated polishing devices cannot reproduce exactly the kinematics of a rolling pneumatic tyre [4, 11-12], more efforts are still desirable to bridge the gap between the friction evolution and surface characteristics.

In this work, the evolution of aggregate surface texture due to the polishing action of genuine pneumatic tyres is investigated with three aggregates. The changes of height distribution, power spectral density and micro-texture in polishing process are estimated to characterize the evolution of aggregate surface texture. A new method to decompose the micro-texture from the whole surface texture is proposed. The method is derived from fractal theory with a sound theoretical background of rubber friction on rough surfaces. The mechanism of friction evolution due to tyre-polishing is suggested.

2 Experimental

2.1 Materials and specimens

Three aggregates were tested, and their mineral compositions are shown in Fig.1. Two rectangle plates were prepared for each type of aggregate. They were obtained by placing manually the aggregates of 0/11 in a single layer, with their flat test faces lying on the bottom of a rectangle mould, then filling the mould with concrete. To accelerate the polishing effect, powder of quartz as wearing agent was added to the polishing flat during polishing process, and its mean particle size was 40 μm.

2.2 Polishing methods

Up to now, there are several polishing machines for simulating the polishing action of pneumatic rubber tyre on aggregate and pavement surface. These simulation methods can be categorized into sliding and rolling modes, based on the principle of the friction between rubber and asphalt surfaces [12]. A review of the existing

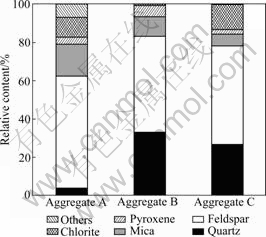
Fig.1 Mineral components of tested aggregates

accelerated polishing devices and measuring methods reveals that most of them do not reproduce exactly the kinematics of a rolling tire and cannot separate polishing from abrasion and breakage. Definitely, there is only a small slip less than 5% between a rolling tire and a road surface due to the tire tread deformation, whereas sliding corresponds to 100% slip. To overcome these drawbacks, a new accelerated polishing machine with genuine pneumatic tyres is adopted in this work, as shown in Fig.2. The machine was developed by the Institute of Road and Traffic Engineering (ISAC), RWTH-Aachen University, Germany. Two genuine car tires with a total load of 1 500 N were used. The tire revolved around a fixed axle at a speed of 9 r/min and rotated around its own axle at a speed of 41 r/min, while the specimens moved back and front at 72 m/min. Powder of quartz was added with an amount of 58 g/min. Water was also injected to the surface of plate during the polishing process. In order to monitor the development of the surface texture and dynamic friction coefficient of the aggregates, the polishing action was accomplished in five stages, as listed in Table 1.

Fig.2 Polishing machine of Aachener

Table 1 Polishing stages and their polishing time

2.3 Texture measurement

FRT laser sensor shown in Fig.3 was used to measure the surface texture profiles. The measured surface area was 10 mm×10 mm and composed of 400 parallel profiles of 10 mm long, spaced at 25 μm and sampled every 2 μm. At each stop, the specimen surface was washed using pure water projected during 600 cone passes before texture measurements. Two plates and totally six surfaces of aggregate particles were measured at each stop. The measured height profiles were firstly filtered for the purpose of de-noising [13-14]. Curving matching methods [15-16] were then adopted to eliminate the transformation due to the measurement error.

Fig.3 Texture profile measuring device and polished specimen

2.4 Friction experiment

Dynamic friction measurements were carried out immediately after texture measurement by the so-called Wehner/Schulze machine system at ISAC (Fig.4). The machine comprises two rotary heads dedicated respectively to polishing and dynamic friction measurement. For the friction measurement, the specimen was launched until a equivalent speed of   100 km/h at its circumference was reached. When the speed reached 90 km/h, water was projected on the specimen surface. At 100 km/h, the motor was stopped and the disc was dropped until the rubber pads touched the specimen surface. The rotation was stopped by friction between the rubber pads and the specimen surface. The braking curves were recorded, as shown in Fig.5. The friction value at 60 km/h was included in the analysis, which corresponded to the measured speed of the

Fig.4 Wehner/Schulze polishing machine

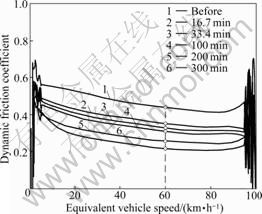
Fig.5 Dynamic friction curves measured with Wehner/Schulzer machine

SCRIM device. Repeated friction measurements until a stable value were reached.

3 Results and discussion

3.1 Friction evolution

The evolutions of dynamic friction coefficient in polishing process are shown in Fig.6. Two distinct phenomena can be observed. Friction of aggregate A firstly increases until reaching a maximum value and then declines to a stable value; while sharp decrease of the friction coefficient is observed in aggregates B and C in the first two polishing stages. The dynamic friction coefficient of aggregates in polishing process reaches its plateau value when the polishing time is over 200 min, which means that the continuing polishing action on friction can be negligible. An improvement of friction in early stage indicates that there is a potential self-sharp effect in aggregate A. More efforts will be required for an insight view of this effect.

3.2 Height profile evolution

The evolutions of height profile due to polishing are illustrated in Fig.7. The phenomenon of global height reduction and differential removal of mineral component can be observed. The polished profile always follows its original shape in waviness band, while the significant changes can be observed at a scale of roughness or

Fig.6 Friction evolutions of tested aggregates

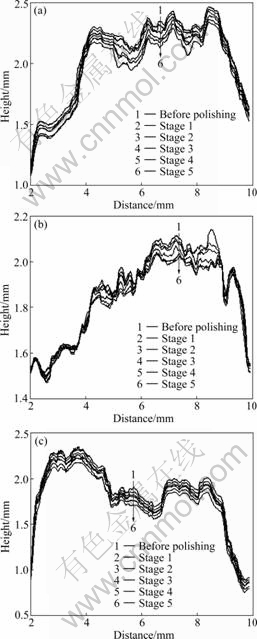
Fig.7 Evolutions of surface profile at section of aggregates:   (a) Aggregate A; (b) Aggregate B; (c) Aggregate C

micro-texture.

As it is critical for theoretical simulation of the fiction coefficient with proper distribution type [11], the surface height distribution of aggregate is approximated with several potential functions, as shown in Fig.8. The statistical results are listed in Table 2. A larger logarithm likelihood value means a better fitting result [17]. According to Fig.8 and Table 2, the Weibull distribution is better in describing the distribution of aggregates surface height.

The fitted surface height distribution curves of aggregate A in polishing process are shown in Fig.9. For comparison, the normalized distribution curves are also plotted in Fig.9. The distribution curves confirm the observed phenomenon of global height reduction and differential removal in micro-scale.

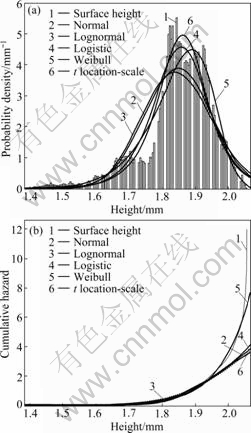
Fig.8 Fitting distributions of aggregate surface height and its cumulative hazards

Table 2 Results of distribution fitting

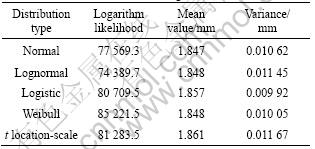
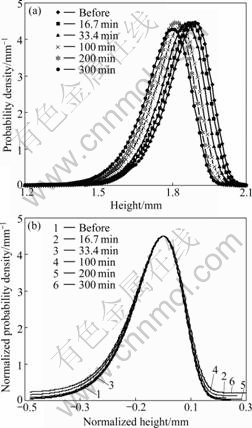
Fig.9 Distributions of surface height profile in process of polishing

3.3 Evolution of power spectral density

Spectral analysis of aggregate surface also confirms the observation. As shown in Fig.10, the power spectral density (PSD) curves exhibit non-linear characteristics. At a long wavelength, no visible changes can be observed, while in a transition wavelength, small changes occur, and at the wavelength less than 40 μm, the curves experience significant variances in polishing process. The changes of surface PSD in micro-scale mean that differential removal of mineral component is the main cause that contributes to friction variations due to the polishing.

3.4 Evolution of micro-texture

As significant changes of PSD mainly occur in a micro-scale, it is critical to decompose the micro-texture from the whole profile within a certain wave length and to explore the changes of micro-texture due to the polishing. Up to now, no precise definition of both micro- and macro-textures in terms of length scales is available. GAL and KL?PPEL [9] have proposed a method to investigate the attribution of micro-texture and macro-texture to friction between rubber and rough surface. They take the cut-off length λ₂ (as shown in Fig.11) as the separate point of micro- and macro-texture. The calculation of the cut-off length λ₂ is based on the

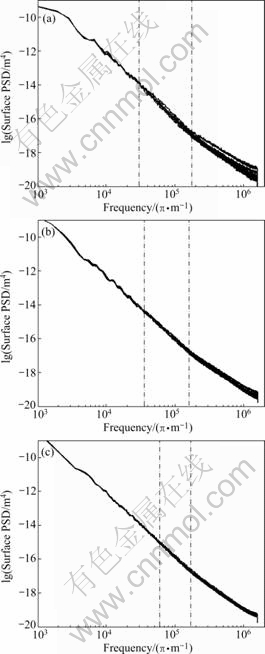
Fig.10 Evolutions of surface PSD: (a) Aggregate A; (b) Aggregate B; (c) Aggregate C

statistical height difference correlation function C_z(λ) [9] schematically shown in Fig.11. This method combined with the moving average filtering methods [13-14] was adopted in this work, and the cut-off length of each profile was used as a moving span to decompose the profile by moving average filtering, as shown in Fig.12.

In order to quantify the changes of the micro-texture, a new parameter named the angle of micro-texture distribution curve is defined, as shown in Fig.13. A larger value of the angle indicates that a rougher surface is rich of micro-texture. The evolutions of micro-texture due to tyre-polishing are summarized in Fig.14. Friction and

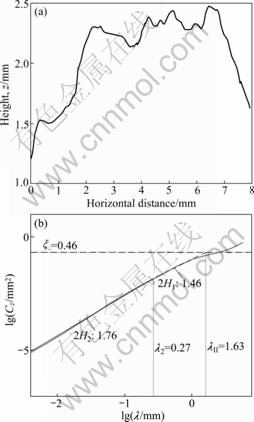
Fig.11 Schematic representation of height difference correlation function and corresponding fractal descriptor

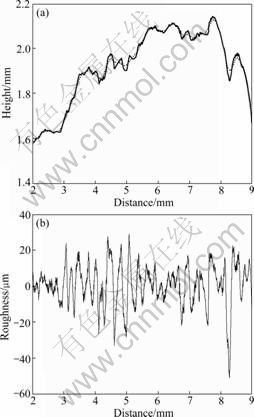
Fig.12 Decomposition of height profile by moving average filtering

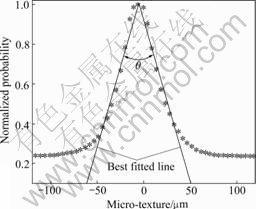
Fig.13 Definition of micro-texture index

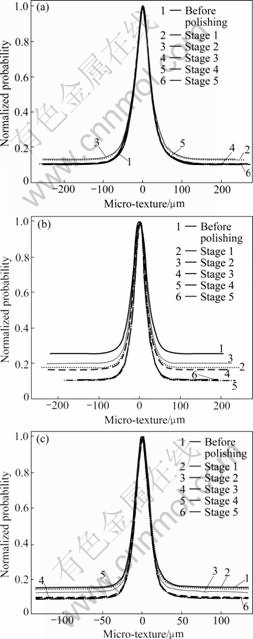
Fig.14 Normalized distributions of micro-texture in polishing process: (a) Aggregate A; (b) Aggregate B; (c) Aggregate C

texture values after polishing are then normalized by their respective values at the initial state and plotted also in Fig.15. It can be seen that the friction evolution is identical to that of the micro-texture index. It is indicated that the evolution of friction coefficient is the consequent changes of micro-texture due to tyre-polishing, which is attributed to the differential removal of mineral component.

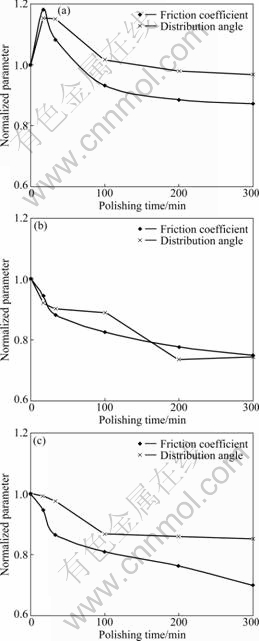
Fig.15 Relations between normalized friction coefficient and distribution angle of micro-texture: (a) Aggregate A;        (b) Aggregate B; (c) Aggregate C

4 Conclusions

1) The distribution of aggregate surface reveals non-Gaussian characteristics and can be approximated by Weibull distribution. The histograms show that global removal of materials during polishing occurs as expected.

2) Changes of the power spectral density in short wave length are primarily caused by the removal of peak asperities and regeneration of micro-texture due to the differential abrasion of mineral components, which consequently affects the value of friction coefficient.

3) The evolution of friction is governed by the micro-texture changes due to the differential removal of mineral component. Generally, the amount of micro-texture decreases with polishing time, while the self-sharpness effect can be expected for certain aggregates.

References

[1] KNILL D G. Petrographical aspects of the polishing of natural roadstones [J]. J Appl Chem, 1960, 10: 28-35.

[2] STEINAUER B, WANG Da-wei, STANJE H, STANJEK C. Improvement of traffic safety due to good grip values during the whole service life of highly stressed roads (mid-term report) [R]. Aachen: RWTH-Aachen University. FE04.208/2007/CRB 1970. 2009. (in German).

[3] DO M-T, TANG Zhen-dong, KANE M, de LARRARD F. Evolution of road-surface skid-resistance and texture due to polishing [J]. Wear, 2009, 66(5/6): 574-577.

[4] KHASAWNEH M A. The development and verification of a new accelerated polishing machine [D]. Akron: The University of Akron, 2008.

[5] WEN Shi-zhu, HUANG Ping. The principle of tribology [M]. 3rd Ed. Beijing: Press of Tsinghua University, 2009: 256-265. (in Chinese)

[6] STEINAUER B, UECKERMANN A, MEYER A, SCHULZE C. Design model for stimulating innovation and competitiveness of small and medium-sized road construction companies. Part II: Design and protection tools for the skid resistance of asphalt pavements [R]. Aachen: RWTH-Aachen University, FKZ: 19W3055B. 2008. (in German)

[7] JENG Yeau-ren, GAO Chih-chung. Changes of surface topography during wear for surfaces with different height distributions [J]. Tribology Transactions, 2000, 43(4): 749-757.

[8] HEINRICH G, KL?PPEL M, VILGIS T A. Evaluation of self-affine surfaces and their implication for frictional dynamics as illustrated with a Rouse material [J]. Computational and Theoretical Polymer Science, 2000, 10: 53-61.

[9] GAL A L, KL?PPEL M. Investigation and modelling of rubber stationary friction on rough surfaces [J]. J Phys: Condens Matter, 2008, 20: 1-13.

[10] PERSSON B N J, ALBOHR O, TARTAGLINO U, VOLOKITIN A I, TOSATTI E. On the nature of surface roughness with application to contact mechanics, sealing, rubber friction and adhesion [J]. J Phys: Condens Matter, 2005, 17: R1-R62.

[11] SCHULZE K H. For the quantitative evaluation of the roughness of road surfaces in relation to the friction in wet conditions, research, road construction and road traffic [R]. Heft 103, 1970. (in German)

[12] DO M-T, ROE P, VOS E, GROENENDIJK J. Tyre and road surface optimisation for skid resistance and further effects: D04 Report on state-of-the-art of test methods for skid resistance [R/OL]. 2009, http://tyrosafe.fehrl.org/.

[13] BALA M, JAY R. Computational surface and roughness metrology [M]. London: Springer-Verlag Limited, 2009: 23-29.

[14] WHITEHOUSE D. Surfaces and their measurement [M]. London: Hermes Penton Science Inc, 2002: 16-47.

[15] KONG Wei-xin, BENJAMIN B K. On solving 2D and 3D puzzles using curve matching [C]// IEEE Computer Society Conference on Computer Vision and Pattern Recognition. 2001: 583-590.

[16] ARMIN G, DEVRIM A. Least squares 3D surface and curve matching [J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2005, 59(3): 151-174.

(Edited by YANG Bing)

Foundation item: Project(50809053) supported by the National Natural Science Foundation of China; Project(FE 04.208/2007/CRB) funded by Federal Highway Research Institute (Bast), Germany

Received date: 2009-10-26; Accepted date: 2010-03-18

Corresponding author: CHEN Xian-hua, PhD; Tel: +86-25-83790522; E-mail: chenxh@seu.edu.cn