Calculation model of edge carbon atoms in graphite particles for anode of lithium-ion batteries
来源期刊:中国有色金属学报(英文版)2011年第11期
论文作者:张万红
文章页码:2466 - 2475
关键词:锂离子电池;碳负极;计算模型;电化学性能;作用机理
Key words:Li-ion batteries; carbon anode; calculation model; electrochemical properties; mechanism of action
摘 要:基于石墨的六角层片模型,通过分析石墨晶体结构及不同位置碳原子的成键特性,提出石墨晶体中的边缘碳原子和基面碳原子具有不同的电化学特性,建立球形石墨颗粒的紧密堆积模型,推导石墨颗粒中表面碳原子(SCA)及边缘碳原子(ECA)分数与石墨的晶体结构参数和颗粒尺寸之间的计算公式,讨论ECA对首次不可逆容量的影响机理并进行验证。结果表明,边缘碳原子的电化学活性较高,易于发生电解液分解并与其它碳原子或基团形成稳固的联接。对于实际石墨颗粒,通过引入相应的修正因子可以修正计算结果,修正后的计算公式可以适用于多种碳材料,如石墨,乱层碳及改性石墨的SCA及ECA分数的计算。
Abstract:
Based on the hexagonal crystallite model of graphite, the electrochemical characteristics of carbon atoms on the edge and basal plane were proposed by analyzing graphite crystal structure and bonds of carbon atoms in different sites. A spherical close-packed model for graphite particle was developed. The fractions of surface carbon atoms (SCA) and edge carbon atoms (ECA) were derived in the expression of crystallographic parameters and particle size, and the effects of ECA on the initial irreversible capacity and the mechanisms of action were analyzed and verified. The results show that the atoms on the edge are more active for electrochemical reactions, such as electrolyte decomposition and tendency to form stable bond with other atoms and groups. For the practical graphite particle, corresponding modifying factors were introduced to revise the difference in calculating results. The revised expression is suitable for the calculation of the fractions of SCA and ECA for carbon materials such as graphite, disordered carbon and modified graphite.

ZHANG Wan-hong
School of Materials Science and Engineering, Henan University of Science and Technology,Luoyang 471003, China
Received 11 October 2010; accepted 25 April 2011
Abstract: Based on the hexagonal crystallite model of graphite, the electrochemical characteristics of carbon atoms on the edge and basal plane were proposed by analyzing graphite crystal structure and bonds of carbon atoms in different sites. A spherical close-packed model for graphite particle was developed. The fractions of surface carbon atoms (SCA) and edge carbon atoms (ECA) were derived in the expression of crystallographic parameters and particle size, and the effects of ECA on the initial irreversible capacity and the mechanisms of action were analyzed and verified. The results show that the atoms on the edge are more active for electrochemical reactions, such as electrolyte decomposition and tendency to form stable bond with other atoms and groups. For the practical graphite particle, corresponding modifying factors were introduced to revise the difference in calculating results. The revised expression is suitable for the calculation of the fractions of SCA and ECA for carbon materials such as graphite, disordered carbon and modified graphite.
Key words: Li-ion batteries; carbon anode; calculation model; electrochemical properties; mechanism of action
1 Introduction
Rechargeable lithium ion batteries have been widely used in consumer electronic and electric vehicle application. The commercial lithium ion batteries are based on carbon anode [1]. Carbonaceous materials in a variety of particle morphologies, size and degree of graphitization are evaluated in Li-ion batteries. In this application, carbon serves as the host substrate for Li ions in the negative electrode. The amount of Li+ that is intercalated or inserted into the carbon structure and the reversibility of the intercalation/deintercalation process depend strongly on the carbon morphology. The irreversible capacity loss associated with the formation of the protective solid-electrolyte interface (SEI) layer varies approximately linearly with the carbon BET specific surface areas [2].
Graphite is used as anode active materials in most commercial production, there are two distinct types of sites on graphite, i.e. basal plane sites which are associated with the carbons forming the surface of the layer planes, and edge sites which involve the terminal sites of the basal planes. The basal plane sites are relatively inactive and the edge plane sites are usually the chemical/electrochemical active sites [3-6]. These studies show that active sites, which are capable of dissociatively chemisorbing oxygen, are present in carbons and they are primarily associated with edge sites or defects on the carbon surface. This observation suggests that the electrochemical and chemical properties of carbonaceous materials should be influenced by the relative fraction of the active sites. It is possible to derive a better understanding of the relationship between the physical properties, chemical reactivity and electrochemical behavior of carbonaceous materials by investigating the fractions of the edge site atoms and basal plane site atoms in the graphite.
The crystallographic structure, surface morphology and physicochemical parameters of carbonaceous materials have dramatically influence on their electrochemical intercalation/deintercalation of Li and the cell performance. Further research on the structure of carbonaceous materials and the unveiling of the correlation between structure and the electrochemical performance gives instruction of the discovery of new electrode materials and the designing of them.
In present work, based on the analysis of general structure unit of graphite and the atom activity difference between basal plane and edge site, the fractions of the edge site carbon atoms (ECA) and the particle surface carbon atoms (SCA) were derived in the expression of crystallographic parameters and particle size, then the relationship among the crystallographic parameters was analyzed. The aim of this effort is to develop a better understanding of the electrochemical performance, active surface area, crystallographic parameters and physical characteristics of various types of carbons, moreover, to explore the modification methods of carbonaceous materials.
2 Structures of graphite and carbon atoms activity
Natural graphite is found in two major crystallographic structures, hexagonal graphite and rhombohedral graphite [7]. The graphite structure consists of carbon atoms arranged in hexagonal rings that are stacked in an orderly fashion (see Fig. 1). Only weak van der Waals bonds exist between these layer planes. The usual stacking sequence of the carbon layers is ABABA … for hexagonal graphite, with a shift of B layers with respect of the A layers. The stacking sequence ABCABC … is found less frequently and is called rhombohedral graphite, where the C layers are shifted with respect to the B layers. Both the structures may be transformed into each other by means of mechanical grinding or heat treatment.
In a graphite particle, on the account of the environmental difference of the sites which are occupied by the atoms, the carbon atoms can be classified as SCA or inner carbon atoms, these two types of atoms have vastly different chemical and electrochemical reactivities. Furthermore, taking account of a graphite crystallite, it has two distinct surfaces, the basal plane and the edge sites. These sites have vastly different chemical reactivities due to their different atomic environment and the saturation of covalent bonds. For example, the oxidation rate and oxygen chemisorption at the edge sites are much higher than those of the basal plane. There are reports [8-11] suggesting that the irreversible capacity loss (ICL) is strongly affected by the relative amount of basal plane and edge sites. These studies conclude that the edge sites are the more active (catalytic) sites for electrolyte decomposition. Every inner carbon atom forms covalent bonds with other three atoms in the neighborhood, which is in bonds saturated state. Meanwhile, there are less than 3 covalent bonds formed in partial carbon atoms of ECA, existing free electrons in sp2-hybridization orbits, these atoms are prone to react with other atoms or complexes under appropriate condition, so the reaction force between ECA and other atoms or complexes is strong, and the bonding is more stable than that between inner atoms and other atoms or complexes. Similarly, as the unsaturated bonds of ECA, they are easy to absorb the other molecules, atoms or ions, and react with them, then ECA exhibits relatively more chemical or electrochemical activity.

Fig. 1 Model of graphite structures: (a) Hexagonal graphite; (b) Rhombohedral graphite
Based on the analyses described above, SCAs on the surface of graphite particles are relatively electrochemical active, and in SCA, ECAs exhibit more active than the others. In the initial charge/discharge cycles of carbon anode, it is mainly ECAs react with electrolytes and Li+ ions to produce compact and stable SEI film, the electrochemical performance of anode is related closely to the fractions of ECA and SCA in graphite. So it is necessary to demonstrate a quantitative analysis about the fractions of ECA and SCA in graphite particles.
3 SCA and ECA in graphite crystallite particles
3.1 SCA and ECA of spherical graphite particles
In the derivation of the fraction of carbon atoms in a graphite crystal for each catalog, it is assumed that: 1) the graphite structure consists of carbon atoms arranged in hexagonal rings and the stacking sequence of the carbon layers is ABABAB …; 2) the graphite crystallites are defect free; 3) there is no impurity atom or complex besides carbon atoms; 4) the graphite particle is ideally sphere, consisting of numerous graphite microcrystallites at specific arrangement.
A crystallite model based on the benzene (n=0) and coronene (n=2) structures shown in Fig. 2 is considerd [12]. The microcrystallite consists of n layers 2-D stretching hexagons which are stacked m layers in the direction perpendicular to the basal plane. Since there are (2n+1) hexagons along the a-axis, the crystallite sizes La and Lc are expressed with the lattice constants a0 and the interlayer spacing c0=2d002 as
![]() (1)
(1)
![]() (2)
(2)
or
![]() (3)
(3)
![]() (4)
(4)
where a0 is the lattice constant; d002 is the interlayer spacing; La is the crystallite size in a-axis direction; Lc is the crystallite size in c-axis direction.

Fig. 2 Crystallite model based on benzene and coronene structure
The number of carbon atoms in a single layer is counted as
![]() (5)
(5)
The number of ECA in a single layer is
![]() (6)
(6)
The total number of ECA in the whole microcrystallite is
![]() (7)
(7)
A graphite particle with radius of R is applied. The arrangements of the microcrystals on the surface of particle have two styles: 1) the basal plane is perpendicular to the surface (Fig. 3(a)); 2) the basal plane parallels to the surface (Fig. 3(b)).
In the former case, the graphite layer planes are perpendicular to the surface of the sphere, the microcrystallites on the surface of the spherical particle is counted as
![]() (8)
(8)
which is calculated by the ratio of the surface area of the particle to the lateral area of a single microcrystallite.
In these microcrystallites, each particle has two lateral faces which are located on the outer surface of the particle, the number of edge side carbon atoms on each lateral face is calculated as
![]() (9)
(9)
Then the total number of ECA on the surface of the particle is
![]() (10)
(10)
The total carbon atoms in a particle NR can be given by the product of the total number of the microcrystallites Nmr and the count of carbon atoms in a single microcrystallite, and Nmr can be expressed by the ratio of the volume of the sphere to the volume of the microcrystallite. Substituting Eqs. (4) and (5), it is obtained that
![]() (11)
(11)
The radius of the graphite particles used in anode materials is of the order of micrometer, for graphite with high crystallinity, the dimension of the graphite crystallites La and Lc is at the range from dozens to hundreds of nanometers, and the crystallographic parameters d002=0.335 43 nm, a0=0.246 12 nm, then, Lc/d002>>1,La/a0>>1, Eqs. (10) and (11) can be simplified as
![]() (12)
(12)
![]() (13)
(13)
The relative fraction of SCA in a graphite particle (i.e., ECA, in this arrangement style) is given as
![]() (14)
(14)

Fig. 3 Arrangement styles of micro-crystals in spherical graphite particle with graphenes perpendicular (a) and parallel to (b) surface of sphere
Another arrangement style for the graphite layer planes parallel to the surface of the particle is consider, the number of the microcrystallites on the surface of the spherical particle is given as
![]() (15)
(15)
Which is described by the ratio of the surface area of the particle to the basal area of a single microcrystallite.
The number of carbon atoms in a single layer and the number of ECA in a single layer are given by Eqs. (5) and (6), respectively, then the number of SCA in the whole spherical particle is obtained.
![]() (16)
(16)
In these SCAs, the number of ECAs is given as:
![]() (17)
(17)
Since La/a0>>1, with simplified Eq.(16), the relative fraction of SCA is described as
![]() (18)
(18)
In these SCAs, the fraction of ECAs is given as
![]() (19)
(19)
3.2 Revision of expression for actual graphite particles
Deriving above for the relative fractions of SCA and ECA in a graphite particle is based on the assumption of an ideal spherical particle, which assumes that the graphite layer planes align regularly and compactly, but in actual graphite particles, there are voids, micropores inside or on the surface of the graphite particle, the solvated Li ions can contact with the inner surface of the micropores, as a result, the fractions of SCA and ECA increase, then the voidage factor ξ and surface micropore-modifying factor η are inducted. Meanwhile, two arrangements of the microcrystallites on the surface of a particle are taken into account: 1) the graphenes are perpendicular to the surface (Fig. 3(a)); 2) the graphenes are parallel to the surface(Fig. 3(b)). However, in practice, the arrangement of the graphite planes is random, then the array-modifying factor ζ is introduced, which is defined as the occurred probability of the graphite basal planes perpendicular to the surface of the particle, then the occurred probability of the graphite basal planes parallel to the surface of the particle is defined as (1-ζ). Eqs. (14), (18) and (19) are modified as
![]() (20)
(20)
![]() (21)
(21)
where e is the relative fraction of SCA in actual graphite particle; e*is the relative fraction of ECA in actual graphite particle; ζ is the array factor, the occurred probability of the graphite basal planes perpendicular to the surface of the particle and 0≤ζ≤1; ξ is the voidage factor, the ratio of the void volume to the volume of the sphere and 0≤ξ<1; η is the surface micropore-modifying factor, the ratio of the surface area of the actual graphite particle to the surface area of the ideal graphite particle and η≥1.
Furthermore, considering the actual graphite powder is aggregate of the variety of particle shape and size, which consists of particles with micropores and the arrangement of the graphite planes is random, the graphite particles count N is assumed with radius Rj (j=1, 2, 3, …, N), then the total fractions of SCA and ECA in actual graphite particle are given as
![]() (22)
(22)
![]() (23)
(23)
4 Main factors affecting fractions of SCA and ECA in graphite particles
4.1 Graphite particle size
Assuming the graphite particle is ideally sphere with radius R, the crystallographic parameters d002= 0.335 43 nm, a0=0.246 12 nm, the crystallite dimensions La=26.9 nm, Lc=28.1 nm (determined by XRD method) are substituted, the effect of graphite particle size on the fractions of SCA and ECA is obtained by Eqs. (14), (18) and (19), corresponding to the two arrangements of the graphite plane, respectively (shown in Fig. 4). It is known that the particle size affects the fractions of SCA and ECA in graphite particle dramatically, as the radius R of the particle increases, the fractions of SCA and ECA decrease, the effect is more remarkable when the particle radius R<10 μm.
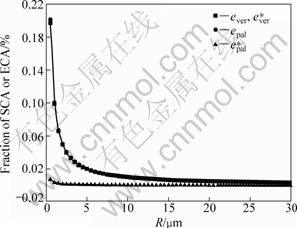
Fig. 4 Effect of particle radius R on fractions of SCA and ECA
The line marked as “■” in Fig. 4 represents the case of the graphite basal planes perpendicular to the surface of the sphere, the fraction of SCA is equal to the fraction of ECA. The lines marked as “●” and “▲” in Fig.4 represent the case of the fractions of SCA and ECA when the graphite basal planes are parallel to the surface of the sphere (see Fig. 3(b)), respectively. From Fig.4, it is seen that there is obvious difference between the fractions of SCA and ECA, when the graphite basal planes are parallel to the surface of the particle. The fraction of ECA is relatively smaller when the graphite basal planes are parallel to the surface of particle than that when the graphite basal planes are perpendicular to the surface of particle, i.e. it attains the least fraction of ECA when the graphite basal planes align themselves concentrically around the sphere center.
4.2 Crystallographic structure of graphite
In the crystallographic parameters of graphite, the lattice constant a0 is basically a constant, the variety of the crystallographic structure reflects on the difference of d002 spacing, average crystallite dimensions La in the graphite lattice plane (a-axis direction) and Lc perpendicular to the graphite plane (c-axis direction). Assuming R=9 μm and a0=0.246 12 nm, the influence of crystallographic parameters, d002 spacing and La on the fractions of SCA and ECA are shown in Figs. 5(a) and (b), respectively. From this relationship, it is apparent that the fraction of SCA in graphite particle increases linearly as the d002 spacing increases, which results in that the count of graphite layer decreases, the amount of atoms decreases in one crystallite and the sum of surface site atoms remains the same, then the fraction of SCA increases. The fraction of ECA increases as the d002 spacing increases and the crystallite dimension La decreases.

Fig. 5 Effect of crystallographic parameters on fraction of SCA (a) and ECA (b)
4.3 Modifying factors
Assuming a spherical graphite particle is formed by microcrystallites in a specific arrangement, and R=9 μm, a0=0.246 12 nm, d002=0.335 43 nm,La=26.9 nm, the influences of modifying factors η, ξ and ζ on the fractions of SCA and ECA are shown in Fig. 6. On the analysis of the influence of a certain modifying factor, for example ζ, the other factors are taken as ideal status, i.e. η=1 and ξ=0. Because of the simple explanation of the fraction of ECA (Eq. 14) when the arrangement style for the graphite layer planes is parallel to the surface of the particle, only the arrangement style for the graphite layer planes perpendicular to the surface of the particle on the analysis of the influence of factors η and ξ is taken into account. As shown in Fig. 6, the fractions of SCA and ECA increase linearly as η increases, the fractions of SCA and ECA increase remarkably as ξ increases; however, the increscent magnitude of ECA is less than that of SCA. The fraction of ECA increases as the array-modifying factor ζ increases, which is defined as the microcrystallites arrangement changes the graphite layer planes from parallel to perpendicular to the surface of the particle. Meanwhile, as the d002 spacing is larger than d100 spacing, there is a looser alignment when the graphite layer planes are perpendicular to the surface of the particle, this results in a bit of decrease of the fraction of SCA, the fractions of SCA and ECA are the same when all the graphite layer planes are perpendicular to the surface of the particle (ζ=1).

Fig. 6 Effect of modifying factors η (a), ξ (b) and ζ (c) on fractions of SCA and ECA for spherical particle
5 Action mechanism of SCA and ECA to electrochemical properties
The ICL observed with carbons in Li-ion batteries is associated with electrolyte decomposition and the formation of SEI layer on the surface of anode materials, which plays a significant role in their electrochemical properties in Li-ion batteries, such as the first-cycle coulombic efficiency, specific capacity of cathode material and the battery. Furthermore, the formation of a uniform, stable, thin and dense SEI layer is a key factor for the excellent cycle performance of Li-ion batteries.
As the SCA of the graphite contacts directly with electrolyte in a practical cell, the electrolyte decomposition and formation of SEI layer on the surface of anode electrode prefer occurring near ECA sites due to its high chemical and electrochemical activities. It seems quite reasonable to predict that the electrolyte decomposition preferentially occurs at the active sites during the first reduction process, so there is a strong combination between SEI and the graphite particle, but its disadvantage is the thicker SEI film formed, which consumes more Li ions. As a result, the coulombic efficiency in the first cycle decreases; on the other hand, the decomposition of electrolyte on the inner graphene plane is slower, there is a poor combination between SEI layer and the graphite particle, but a thinner SEI film results in high coulombic efficiency and poor cycle performance. Moreover, the anode materials with high fraction of ECA exhibit a decreased polarization between charge and discharge, or so-called hysteresis, which is favorable to decreasing the internal resistance and improving the rate capability of cells.
5.1 Action of BET specific surface area
On the assumption of the same physicochemical parameters except BET specific surface area(SSA) for graphite particles, the sample with opening micropores, nano-channels and large voidage exhibits a large BET specific surface area, the influence of SSA on the fractions of SCA and ECA can be demonstrated by voidage factor ξ and surface micropore-modifying factor η in Eqs. (20) and (21), respectively. ξ represents the ratio of the void volume to the volume of the sphere, and η represents the ratio of the surface area of the actual graphite particle to the surface area of the ideal graphite particle. From Eqs. (20) and (21), it it shown that the fractions of SCA and ECA increase as ξ and η increase (means a large number of micropores on the particle surface and a large value of voidage), resulting in a large ICL in the first cycle, i.e., a larger SSA of the graphite particle results in a larger ICL of the cell.
5.2 Action of particle size
From Eqs. (20) and (21), it can be expected that the fractions of SCA and ECA decrease as the particle radius R increases. As a result, the ICL of the cell decreases due to the less Li-ion consumption in the formation of SEI layers and the electrochemical properties of anode materials are improved.
Nevertheless, the analysis above of the action mechanism of particle size to the electrochemical properties of anode materials is based on the consumption of omitting other factors. But in actual, when the particle size is too large, it is hard to make the electrode uniformly, resulting in the increase of diffusion distance of Li-ion in the graphite particles and poor charge/discharge performance of Li-ion batteries. The action mechanism of particle size in the precondition is in a certain range of magnitude but not unlimited.
5.3 Action of crystallographic structures
The crystallographic parameters of carbon La and Lc increase, and d002 spacing decreases as it transforms from amorphous structure to ideal crystalline structure, but there is nearly no change of its d100 spacing.
Eqs. (20) and (21) show that the influence of crystallographic structures on the fractions of SCA and ECA in graphite particle is presented by the change of average crystallite dimensions La in the graphite lattice plane and d002 spacing. From highly disordered hard carbons to highly graphitic carbons, the crystallographic parameters La increases and d002 spacing decreases, resulting in a decrease in the fractions of SCA and ECA and in ICL of the cell, and an improved electrochemical performance.
6 Experimental verification and application
6.1 Verification of action mechanism of SCA and ECA
Research on the relationship between physical parameters of graphite powder and its electrochemical performance is carried out, natural flake graphite is prepared by pulverizing process, and various size of spherical graphite is made by spheroidizing and sieving process, the physical parameters of natural graphite powders and their initial irreversible capacity are listed in Table 1.
From Table 1, it is apparent that the NFG exhibits large ICL and SSA, the ICL increases with the increase of SSA and the decrease of particle size for spherical graphite (SG) samples, which shows good agreement with the action mechanism of particle shape, size and specific surface area. Other researchers [7] also presented the relationship between Qirr and the BET surface area (SBET) of carbon. The data obtained with natural graphite in LiClO4 in 50% ethylene carbonate+50% dimethyl carbonate (volume fraction) show a linear relationship expressed as:
Qirr =7.13+7.10SBET (24)
All these results give an experimental verification for the analysis above.
On account of the relationship between the crystallographic structure of carbonaceous materials and reversible capacity or ICL of Li-ion batteries, as it is well known, soft carbons are carbon materials, the structure of which evolves progressively toward the graphite structure when they are heat-treated at high temperature, up to 3 000 °C. They consist of more or less misoriented crystallites, the size and crystalline order of which increase with the heat treatment temperature (HTT). At the beginning of the graphitization step (HTT≈1 200- 1 300 °C), the size of the crystallites is of the order of 5 nm both parallel and perpendicular to the layers (La and Lc, respectively), with an average interplane distance d002 close to 0.344 nm. The crystallite size is about 10 nm at HTT≈2 000 °C and reaches several dozens of nanometers at higher HTT, while d002 approaches the graphite value (0.335 4 nm). Typical soft carbons are graphitizable cokes, ex-mesophase carbon fibers, vapor-grown carbon fibers or mesocarbon microbeads (MCMB). The experimental results of FLANDROIS and SIMON [13] are shown in Table 2 for a series of heat-treated petroleum cokes, the irreversible losses decrease with HTT except for the HTT-2800 sample. As in highly graphitized samples (HTT=2 800 °C and above), some exfoliation occurs, producing an increase of irreversible capacity losses.
Table 1 Physical parameters of natural graphite powder
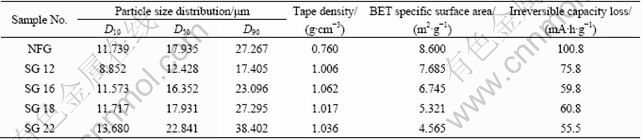
Table 2 Electrochemical data, d002 spacing and g deduced from X-ray diffraction measurements of heat-treated petroleum cokes*

Considering the effect of the crystallographic structure of anode on the ICL, BARSUKOV [14] reported the electrochemical properties of a natural graphite (with high crystallinity from Superior Graphite, Chicago, IL, USA.), hard carbon (grade Carbotron of Kureha Co., Tokyo, Japan) and graphitized mesophase material (grade MCMB2528 of Osaka Gas Co., Tokyo, Japan) as presented in Table 3. These results show that purified natural graphite has the highest capacity intermediate ICL. The irreversible capacity is favorable in the case of MCMB2528 (graphitized soft carbon, with larger La, Lc and the smallest d002 spacing). The hard carbon (with a larger d002 spacing, less Lc and La) exhibits low capacity and higher irreversible capacity loss. This gives the evidence of the analysis above for the action mechanism of ECA and SCA.
Moreover, about the dependence of ICL on crystallographic parameter La, RADOVIC et al [15] suggested a connection between the crystallite diameter La and the active surface area, i.e., the concentration of active sites decreases with an increase of La. TRAN et al [16] presented experimental results for ICL and physical properties, i.e., crystallographic parameters and BET surface area of various carbons. Both hard and soft carbons are included in their study, as well as different electrolytes. The data compiled for ICL are plotted as a function of 1/La in Fig. 7. The scatter in the plot is large, which attributes to the use of data for both hard and soft carbons, as well as the different conditions used to obtain the ICL results. Despite this scatter, it is believed that the trend shows that ICL is inversely proportional to La, and they even gave the relationship between ICL (Lic) and La as
Lic=K/La (25)
where K is a proportionality constant that is a function of the reactivity of the edge sites and the number of crystallites in the particle. This relationship is consistent with the predicted result from Eq.(21). As discussed above, the experimental results give verification for the analysis of the action mechanism of crystallographic structures to ICL.
Table 3 Electrochemical characteristics at C/20 rate of commercial hard carbon, MCMB2528 and natural graphite (LBG1025) in half cells with EC-DMC (1:1) and LiPF6 (1 mol/L)


Fig. 7 Relationship between ICL vs 1/La (Line indicates trend of data)
6.2 Mechanism and application of mechanical modification and mild oxidation of graphite
It was reported by PELED et al [17] that mild oxidation of artificial graphite could modify its electrochemical performance as anode material for lithium ion batteries. Some researchers [18-19] claimed that the electrochemical properties of natural flake graphite could be improved by mechanical process, such as milling, pulverizing and spheroidizing.
The mechanical modification of graphite includes the following processes: 1) the particle size is decreased by pulverizing; 2) the edge sides and defects of the flake graphite are removed to form spherical or near-spherical particle morphology by means of jet milling or mechanical force; 3) a proper particle size distribution is obtained by sieving. The mechanical modification described above could remove most of the edge side and defects which exhibit more activity, resulting in a great decrease in the surface area and structural defects, and an increase in tap density and the arrange regularity of microcrystallites. Consequently, there is a decrease in the fractions of ECA and SCA, and the electrochemical performance of the anode improves.
In the same way, the mild oxidation of natural graphite could modify its electrochemical performance as anode materials for Li-ion batteries. The major processes during mild oxidation can be summarized as follows: 1) the metastable structures are removed, such as dislocations and stress, which are produced during the pulverizing and sieving process; 2) some active sites and/or defects in materials are removed, resulting in the improvement of surface structure and crystallographic structure, the decrease of SCA and ECA fractions; 3) the sharp corners and edge sides of the graphite particles are oxidized preferentially, then the surface of the particles and its mocropores become smoother, the λ value decreases, the fractions of SCA and ECA decrease; 4) the particle radius R decreases, resulting in the increase of SCA and ECA; 5) the diameter of the micropore and the width of nanochannel increase, resulting in the increase of SCA and ECA.
There is a competition among the different action results mentioned above when the modification process is carried out. Under mild oxidation condition, the former three action results predominate, the fractions of SCA and ECA in the graphite decrease, and the ICL decreases consequently. The increase in degree of graphitization and regularity of the micro-crystallite arrangement results in an increase of reversible capacity of the anode materials. Meanwhile, the smoother surface of the graphite particle is favorable for the formation of an uniform and dense SEI layer, therefore, an improvement in the integrate electrochemical performance of the anode materials is achieved.
6.3 Mechanism and application of coating modification of graphite
It is known that pitch or resin can be coated onto graphite as precursors to form a “core-shell” structure, then the precursors are transformed into turbostratic disordered carbon during the succedent heat treatment. The electrochemical properties of the modified graphite are improved remarkably [20-23].
Considering a highly crystalline natural graphite, there is a significant difference between the electrochemical activity of SCA, ECA and the inner basal plane atoms, and there is a large dimension of its La and Lc. Therefore, the electrochemical activity of different sites on the surface of the graphite particles is not uniform, and the SEI layer formed in the sites of ECA is denser and stronger than that formed in the sites of basal plane atoms. As a result, the SEI layer formed in the electrode is local thinner or local thicker, i.e. it is not favorable for natural graphite to form a thin and dense SEI layer, which effects its cycling performance.
When natural graphite is coated with a layer of pitch or resin pyrolytic carbon, which is classified as turbostraticly disordered carbon, having a very little crystallite domain and dimension of Lc, La is significantly smaller than that of the pristine graphite. The activity of the atoms on the particle surface is relatively uniform, as a result, a dense SEI layer forms during the first charge/discharge cycle. Furthermore, defects such as dislocations and deformation are partially removed during carbonizing or graphitizing heat treatment process, resulting in a more regular and dense arrangement of graphite microcrystallites, then a higher Li-intercalation capacity is achieved. Another action is the mild oxidation of the graphite during the heat treatment process when an oxidizing atmosphere is formed by the pyrolytic production of H2O and CO2 gas. The sharp corners and edge sides of the graphite particles are oxidized preferentially, then the surface of the particles becomes smoother, and the ICL decreases.
As mentioned above, the difference in reaction activity of SCA decreases after surface coating modification process, it is favorable to forming a thin, regular and stable SEI layer; the mild oxidation action during the subsequent heat treatment results in an increase of regularity of the micro-crystallite arrangement, then the Li-intercalation capacity increases and the improvement in the integrate electrochemical performance of the anode materials is achieved.
7 Conclusions
1) Based on the analysis of general structure unit of graphite and its atoms activity difference between basal plane and edge site, the atoms on the edge are more active for electrochemical reactions and tend to form stable bond with other atoms and groups. The fractions of ECA and SCA in graphite particles play an important role in the electrochemical performance of anode materials.
2) A spherical close-packed model for graphite particle is developed. The fractions of surface carbon atoms (SCA) and edge carbon atoms (ECA) are derived in expression of crystallographic parameters and particle size.
3) For the practical graphite particle, the corresponding modifying factors are introduced to revise the difference in calculating results. The effects of ECA on the initial irreversible capacity and the mechanisms of action are analyzed and verified.
References
[1] GUO Hua-jun, LI Xin-hai, XIE Jie, WANG Zhi-xing, PENG Wen-jie, SUN Qian-ming. Effects of Ni substitution on the properties of Co3O4/graphite composites as anode of lithium ion batteries [J]. Energy Conversion and Management, 2010, 51(2): 247-252.
[2] ZAGHIB K, NADEAU G, KINOSHITA K. Influence of edge and basal plane sites on the electrochemical behavior of flake-like natural graphite for Li-ion batteries [J]. J Power Sources, 2001, 97-98: 97-103.
[3] PRASAD K S, MUTHURAMAN G, ZEN J M. The role of oxygen functionalities and edge plane sites on screen-printed carbon electrodes for simultaneous determination of dopamine, uric acid and ascorbic acid [J]. Electrochemistry Communications, 2008, 10(4): 559-563.
[4] HALLAM P M, BANKS C E. Quantifying the electron transfer sites of grapheme [J]. Electrochemistry Communications 2011, 13(1): 8-11.
[5] LEE Y T, YOON C S, SUN Y K. Improved electrochemical performance of Li-doped natural graphite anode for lithium secondary batteries [J]. J Power Sources, 2005, 139(1-2): 230-234.
[6] SETHURAMAN V A, HARDWICK L J, SRINIVASAN V, KOSTECKI R. Surface structural disordering in graphite upon lithium intercalation/deintercalation [J]. J Power Sources, 2010, 195(1): 3655-3660.
[7] KINOSHITA K, ZAGHIB K. Negative electrodes for Li-ion batteries[J]. J Power Sources, 2002, 110(2): 416-423.
[8] ZAGHIB K, SONG X, GUERFI A, KOSTECKI R, KINOSHITA K. Effect of particle morphology on lithium intercalation rates in natural graphite [J]. J Power Sources, 2003, 124(2): 505-512.
[9] VERMA P, MAIRE P, NOV?K P. A review of the features and analyses of the solid electrolyte interphase in Li-ion batteries [J]. Electrochimica Acta, 2010, 55(22): 6332-6341.
[10] CHUNG G C, JUN S H, LEE K Y, KIM M H. Effect of surface structure on the irreversible capacity of various graphitic carbon electrodes [J]. J Electrochem Soc, 1999, 146(5): 1664-1671.
[11] ZAGHIB K, NADEAU G, KINOSHITA K. Effect of graphite garticle size on irreversible capacity loss[J]. J Electrochem Soc, 2000, 147(6): 2110-2115.
[12] FUJIMOTO H, SHIRASHI M. Characterization of unordered carbon using Warren–Bodenstein’s equation [J]. Carbon, 2001, 39(11): 1753-1761.
[13] FLANDROIS S, SIMON B. Carbon materials for lithium-ion rechargeable batteries [J]. Carbon, 1999, 37(2): 165-180.
[14] BARSUKOV I V. New carbon based materials for electrochemical energy storage systems [M]. Netherlands: Springer, 2006: 213-218.
[15] RADOVIC L, WALKER P, JENKINS R. Importance of carbon active sites in the gasification of coal chars [J]. Fuel, 1983, 62(7): 849-856.
[16] TRAN T, YEBKA B, SONG X, NAZRI G, KINOSHITA K, CURTIS D. Thermal and electrochemical studies of carbons for Li-ion batteries: 2. Correlation of active sites and irreversible capacity loss [J]. J Power Sources, 2000, 85(2): 269-278.
[17] PELED E, MENACHEM C, BAR-TOW D, MELMAN A. Improved graphite anode for lithium-ion batteries chemically bonded solid electrolyte interface and nanochannel formation [J]. J Electrochem Soc, 1996, 143(1): L4-L7.
[18] GUO Hua-de. A kind of spherical graphite processing methods and systems: China, CN200710132665.8 [P]. 2009-3-25. (in Chinese)
[19] WANG Guo-ping, ZHANG Bao-lan, YUE Min, XU Xiao-luo, QU Mei-zheng, YU Zuo-long. A modified graphite anode with high initial efficiency and excellent cycle life expectation[J]. Solid State Ionics, 2005, 176(9-10): 905-909.
[20] ZHOU You-yuan, LI Xin-hai, GUO Hua-jun, WANG Zhi-xing, YANG Yong. Study on the performance of carbon-graphite composite coated by pitch [J]. Journal of Functional Materials, 2007, 38(6): 955-957. (in Chinese)
[21] ZHANG Xiao-lin, WANG Cheng-yang, MA Tie, WANG Mei-xian. Investigation on pitch coated natural graphite as the cathode material for Li-ion battery [J]. Carbon, 2006(4): 8-11.(in Chinese)
[22] YANG Shao-bin, FEI Xiao-fei, QI Rui-ping, WANG Huan, MENG Li-na, JIAO Jian. Influence of petroleum pitch coating graphite on electrochemical performance of lithium ion battery [J]. Chinese Journal of Power Sources, 2008, 32(11): 745-747. (in Chinese)
[23] XU Le, LIU Hong-bo, LI Fu-jin, HE Yue-de. Effect of PF resin-coating on nature microcrystalline graphite used as anode materials of Li-ion batteries [J]. Non-Metallic Mines, 2010, 33(1): 24-27. (in Chinese)
[24] ZHENG T, LIU Y H, FULLER E W, TSENG S, SACKEN U V, DAHN J R. Lithium insertion in high capacity carbonaceous materials [J].J Electrochem Soc, 1995, 142(8): 2581-2590.
[25] JUNG Y, SUH M C, SHIM S C, KWAK J. Lithium insertion into disordered carbons prepared from organic polymers [J]. J Electrochem Soc, 1998, 145(8): 3123-3129.
[26] XIANG Hong-qi, FANG Shi-bi, JIANG Ying-yan. Carbonaceous anodes for lithium-ion batteries prepared from phenolic resins with different cross-linking densities [J]. J Electrochem Soc, 1997, 144(7): L187-L190.
[27] JUNG Y, SUH M C, LEE H, KIM M, LEE S, SHIM S, KWAK J. Electrochemical insertion of lithium into polyacrylonitrile-based disordered carbons [J]. J Electrochem Soc, 1997, 144(12): 4279-4281.
[28] TATSUMI K, ZAGHIB K, SAWADA Y, ABE H, OHSAKI T. Anode performance of vapor-grown carbon fibers in secondary lithium-ion batteries [J]. J Electrochem Soc, 1995, 142(4): 1090-1096.
[29] IIJIMA T, SUZUKI K, MATSUDA Y. Electrodic characteristics of various carbon materials for lithium rechargeable batteries [J] Synthetic Metals, 1995, 73(1): 9-20.
张万红
河南科技大学 材料科学与工程学院,洛阳 471003
摘 要:基于石墨的六角层片模型,通过分析石墨晶体结构及不同位置碳原子的成键特性,提出石墨晶体中的边缘碳原子和基面碳原子具有不同的电化学特性,建立球形石墨颗粒的紧密堆积模型,推导石墨颗粒中表面碳原子(SCA)及边缘碳原子(ECA)分数与石墨的晶体结构参数和颗粒尺寸之间的计算公式,讨论ECA对首次不可逆容量的影响机理并进行验证。结果表明,边缘碳原子的电化学活性较高,易于发生电解液分解并与其它碳原子或基团形成稳固的联接。对于实际石墨颗粒,通过引入相应的修正因子可以修正计算结果,修正后的计算公式可以适用于多种碳材料,如石墨,乱层碳及改性石墨的SCA及ECA分数的计算。
关键词:锂离子电池;碳负极;计算模型;电化学性能;作用机理
(Edited by FANG Jing-hua)
Foundation item: Project (09001232) supported by the Doctoral Foundation of Henan University of Science and Technology, China
Corresponding author: ZHANG Wan-hong; Tel: +86-379-64231846; Fax: +86-379-64230597; E-mail: wh-zhang@tom.com
DOI: 10.1016/S1003-6326(11)61038-8

