DOI:10.19476/j.ysxb.1004.0609.2019.05.13
一种基于镍基高温合金成分的雀斑预测模型
包超君1,李振锋2,刘 锋1,江 亮1
(1. 中南大学 粉末冶金国家重点实验室,长沙 410083;2. 株洲中航动力精密铸造有限公司,株洲 412000)
摘 要:针对当前雀斑判据在合金成分上存在的不足,构建一个基于高温合金成分的雀斑预测模型并对其进行了验证。通过对合金各元素的密度溶质膨胀系数β和密度温度膨胀系数βT的计算,定量分析其在凝固过程中对糊状区液相密度的影响。通过定义一个雀斑形成倾向因子P,量化各个元素对雀斑形成的影响大小。并在此基础上,构建一个虑及合金成分的雀斑预测模型,该模型可以预测不同组分的合金和雀斑形成之间影响规律。3种不同来源的k值(如实验值、二元合金相图和Thermo-Calc计算的平衡分配系数)被代入该模型计算,验证哪种k值能更好地预测雀斑形成。结果表明:基于二元合金相图的k值,预测结果与实验结果拟合较差,其线性拟合优度R2最大时仅为0.4;而采用实验和Thermo-Calc的k值,拟合较好,v2最大值分别达到0.87和0.95。最后,计算SX系列合金的P值,结果显示:单位含量的Hf元素对雀斑有最强的抑制作用,Ta元素的抑制作用次之;Al、Re元素对雀斑有较强的促进作用,W元素的促进作用次之。
关键词:雀斑;高温合金;成分;雀斑形成倾向因子;平衡分配系数;预测模型
文章编号:1004-0609(2019)-05-0998-10 中图分类号:TG146.1 文献标志码:A
雀斑是铸造高温合金一种常见的宏观偏析缺陷,严重影响铸件的性能,而且在后续均匀化及热处理中又难以消除,有雀斑的铸件必须要废弃,造成极大的经济损失。为了有效预测和控制雀斑缺陷的产生,许多研究者针对雀斑的预测模型展开研究,并建立了一系列相关判据[1-2]。其中,瑞利数(Rayleigh number)判据综合考虑了合金成分及凝固参数等因素的影响,得到广泛应用[3-8]。
瑞利数(Ra)最初是为了研究流体力学失稳现象而提出的一个无量纲参数,它表征了形成对流时的驱动力与粘滞阻力之间的比值,其表达式如下[5]:
 (1)
(1)
式中:Δρ/ρ0为糊状区液相密度差;Π为液相渗透率;h为糊状区高度;α为热扩散系数; 为运动黏度。当对流驱动力大到足以克服液相间的粘滞阻力时,就会有对流形成,这里存在一个临界的转变点,记为临界瑞利数Racrit。研究者可以通过比较体系中Ra与Racrit大小来判定凝固过程中是否有对流出现,进而推测有无雀斑形成。
为运动黏度。当对流驱动力大到足以克服液相间的粘滞阻力时,就会有对流形成,这里存在一个临界的转变点,记为临界瑞利数Racrit。研究者可以通过比较体系中Ra与Racrit大小来判定凝固过程中是否有对流出现,进而推测有无雀斑形成。
忽略合金成分的影响,则式(1)可以简化为 (2)
(2)
式中:G为温度梯度;v为凝固速率;Racrit_1为只考虑凝固参数时的临界瑞利数值。这里a和b的数值跟研究者选取的瑞利数判据及研究对象有关,比如针对某单晶高温合金SX-1,BECKERMANN等[5]的G-2/3v-5/3< 0.25和POLLCOK[8]的G-1/2v-1/4<0.949。通过式(2)可知合金在哪种工艺条件下才会有雀斑生成。
在只考虑合金成分时,瑞利数判据可以得到另一个简单的形式(Racrit_2为只考虑合金成分时的临界瑞利数值):
 (2)
(2)
式中:Racrit_2为只考虑合金成分时的临界瑞利数值。
LONG等[9]和王玲等[10]等通过计算Δρ/ρ0的大小来比较了几种不同系列高温合金在凝固过程中产生雀斑的能力。但是,他们研究的是合金体系整体的液相密度变化,并未就单个元素对液相密度及雀斑形成可能性大小进行计算,因此并不能明确指出什么样成分构成的合金容易形成雀斑。当前已有相关研究者就合金元素对糊状区液相密度及雀斑形成展开研究,封少波等[11]研究了元素偏析对DZ483合金糊状区液相密度的影响,而TIN等[12]的研究表明,W、Re元素对雀斑有促进作用,而增加Ta的含量有利于抑制雀斑的产生。但是这些多是定性分析,并没有把这种元素对形成雀斑的抑制或促进作用量化。有必要定量分析高温合金各个元素对糊状区液相密度的影响大小,这对合理设计合金成分和选择适当的工艺条件来避免雀斑的出现,乃至建立完备的雀斑预判机制都具有重要意义。
因此,本文作者在当前瑞利数判据的基础上,通过量化各元素对液相密度及雀斑形成的影响大小,构建了一个基于高温合金成分的雀斑预测模型。该模型可以预测不同合金组分与雀斑形成之间的影响规律,并展示该模型所需变量的计算及建模过程,并就文献中的实验数据,对模型进行了验证。
1 基于合金成分的雀斑预测模型建立
为了明确各个合金元素对雀斑形成的影响,定义一个新的因子P,称为元素的雀斑形成倾向因子,用来表征各元素含量Ci对雀斑形成的影响大小。则式(2)可以变换为
 (3)
(3)
显然,若Pi>0,则说明添加该元素会使得糊状区液相密度增加,抑制雀斑的形成;若Pi<0,则添加该元素会使得糊状区液相密度减少,促进雀斑的形成。这里Pi的绝对值大小,反映了单位含量下该元素对雀斑形成的抑制或促进作用大小。
1.1 雀斑形成倾向因子P的计算
各元素的P值与其对糊状区液相密度的影响有关,而高温合金液相密度是各元素偏析和温度梯度共同作用的结果,则式(3)可变换为[13]
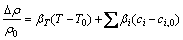 (4)
(4)
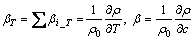 (4a)
(4a)
式中:βi_T为元素i的密度温度膨胀系数(K-1);βT为体系的密度温度膨胀系数(K-1);βi为元素i的密度溶质膨胀系数。式(4)中右侧第一项为各元素由于温度变化导致的相对密度变化,第二项为各元素偏析作用导致的相对密度变化。
由液相斜率m=dT/dC,代入式(4)中,则:
 (5)
(5)
假设合金凝固过程遵循Scheil或Lever模型,则在某一凝固时刻fs时,各元素的液相浓度ci为
 (6)
(6)
代入式(5),则
 (7)
(7)
则各元素雀斑形成倾向因子Pi为:
 (8)
(8)
从式(8)上看,P的值除与所选的凝固模型有关外,主要与各元素的液相线斜率m,平衡分配系数k,β和βT有关。
1.2 密度温度膨胀系数βT和密度溶质膨胀系数β的计算
对于高温合金来说,其固相线温度一般在1300 ℃以上,在这种高温下,普通的实验方法难以对其糊状区液相密度进行测量。根据摩尔分数法[14-15]对液相密度ρ进行计算:
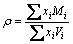 (9)
(9)
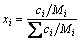 (10)
(10)
 (11)
(11)
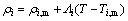 (12)
(12)
式中:xi、Mi、Vi分别为元素i的摩尔分数,摩尔质量和摩尔体积;Vm为元素i在其熔点Tm时的摩尔体积;αi为元素i体积膨胀系数;Λi为元素i的密度温度系数,并有Λ=-αρm。
以二元合金Ni-A为例,若其某一凝固时刻两元素的浓度分别为cNi和cA,则
 (13)
(13)
这里,对于任意凝固时刻有cNi+cA=100。
对式(13)求微分,得:
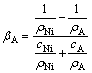 (13a)
(13a)
 (13b)
(13b)
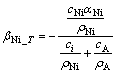 (13c)
(13c)
推广到多元合金体系,则
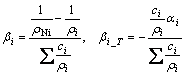 (13d)
(13d)
为简化计算,以各元素熔点时的密度值ρm代替ρ,则
 (14)
(14)
1.3 模型建立
根据式(8)和式(14),便可以求得各元素的P值大小。再通过式(3)计算各元素初始成分c0与P值的乘积之和,便可以求得不同组分的合金在凝固过程中糊状区液相相对密度差△ρ/ρ0,并以此来预测合金在凝固过程中有无雀斑生成。当其值小于某个临界值时,该合金将有雀斑产生。
在结合凝固参数的影响之后,则有
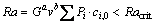 (15)
(15)
2 模型验证
2.1 雀斑实验数据[7]
Pollcok统计了在同一凝固参数下,10组SX系列合金产生的雀斑数量,10组合金成分如表1所列,雀斑数量(95%置信区间)如图1所示。
这里以这10组合金为计算对象,利用本实验中介绍的方法得到各组合金的△ρ/ρ0的值,并与它们实际的雀斑数量进行比较。若不同合金的△ρ/ρ0值与其雀斑数量存在某种联系,本文作者认为该模型可以用来预测雀斑。
2.2 模型参数计算
2.2.1 SX系列合金的β和βT的计算
对SX系列合金计算β和βT的结果如图2(a)和(b)所示,采用的各元素物理性质如表2[15]所示。
表1 实验所用单晶合金成分
Table 1 Compositions of experiment single-crystal alloys

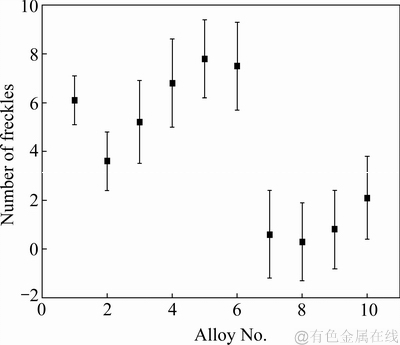
图1 各组合金95%置信区间下产生雀斑的平均数量
Fig. 1 Mean number of freckles in each alloy associated 95% confidence intervals
从图2可以得知,元素含量的改变对其溶质膨胀系数影响很小,基本可以认为是一个恒定值,而对温度膨胀系数,某些元素含量的改变对其影响较大,如Al、Co元素。
表3列出了同一元素β与mβT数值上的比较(这里液相线斜率m值的来自二元合金相图,如表4所示),可以看到,即使是差异最小的c0元素,两者之间数值大小也相差20倍以上,而对于Hf元素来说,两者的差异达到3000倍以上。可见,同一元素溶质偏析对糊状区液相密度的影响远大于温度梯度对其的影响。基于此,忽略其温度的影响,只考虑溶质偏析作用,则P值计算如下:
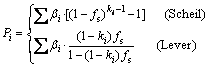 (16)
(16)
对SX系列合金来说,其各元素的溶质膨胀系数如下:βAl=-0.022,βCr=-0.0024,βCo=0.00018,βRe0.0055,βTa=0.0045,βHf=0.0033,βW=0.0052,βMo= 0.0015。
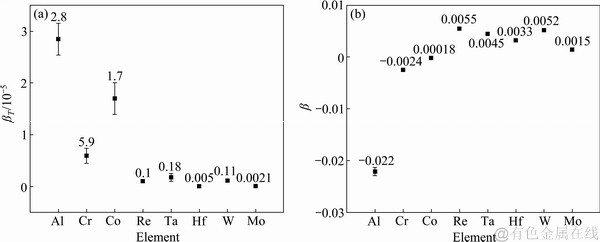
图2 SX系列合金中各元素密度的热膨胀系数和溶质膨胀系数
Fig. 2 Thermal expansion coefficient (a) and solutal expansion coefficient (b) of density for each element in SX alloys
表2 液态金属单质的物理性能
Table 2 Physical properties of liquid metals
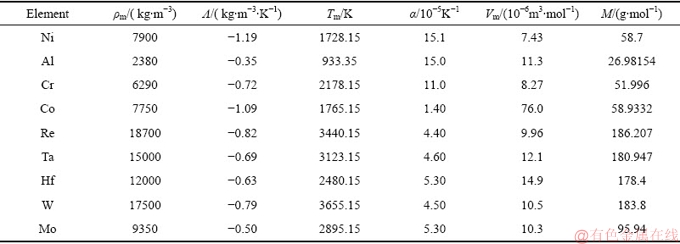
表3 β与mβT的比较
Table 3 Difference between β and mβT

2.2.2 凝固分数fs的选取
目前研究者对于雀斑的起源位置还有所争议,HUNT等[16]认为引起雀斑形成的对流扰动最初起源于糊状区底部;而MARGIRL等[17]和 SARAZIN等[3]认为对流扰动是由靠近液相线附近的低密度液相层引起的,雀斑通道随机的在枝晶尖端前沿形成,随后蔓延到枝晶深处;AUBURTIN等[18]认为雀斑通道形成于fs=0.5;MA等[19]在对CMSX-4试样的微观组织观察中发现,雀斑最初形成处其液相分数要高于0.5。同时,不同瑞利数判据取得最大值的位置也不尽相同,如BECKERMANN等[5]的瑞利数判据最大值在fs=0.1~ 0.15;而YANG等[6]的瑞利数判据最大值在fs=0.4~0.6。有鉴于此,选取了fs为0.1、0.5和0.9作为3个不同的液相密度计算的位置点。
2.2.3 平衡分配系数k的计算
从式(14)可以看出,P值的计算与k值密切相关,为了保证本模型的精确性,这里k值的选取采用3种方法:1) 基于实验测得的k1值;2) 基于二元镍基合金相图[20],作两条从零成分点出发并沿着固、液相线的切线,计算得到k2值。3) 基于Thermo-Calc,计算SX1~10这10组合金在不同凝固分数fs(0.1、0.5和0.9)时的平均k3值。3种方法计算的k值如表4所示。
2.3 验证结果与讨论
分别就两种凝固模型Scheil和Lever,计算了SX1~10这10组合金在不同凝固时刻(fs=0.1,0.5和0.9)糊状区液相相对密度差△ρ/ρ0。其中Thermo-Calc得到的k值进行了Lever计算。
2.3.1 采用实验测得的k值
图3和4所示分别为在不同凝固模式下基于实验测得的k值计算的雀斑数量与液相相对密度差之间的关系。可以发现,雀斑数量与液相密度差之间存在一定的线性关系,液相密度差越小,合金产生的雀斑数量也越少。同时,拟合优度R2的值也随fs的增加而增加,而越趋向于1,在fs=0.9时,R2值在Scheil和Lever模式下分别为0.87和0.86。该结果表明,通过本模型计算合金液相相对密度差能够预测雀斑生成情况。两种凝固模型在拟合实验值的时候,拟合效果相差不大。
表4 三种不同方法的合金各元素平衡分配系数ki和液相线斜率m
Table 4 Equilibrium distribution coefficients(ki) and liquidus slopes(m) in three different methods for SX alloys

2.3.2 采用二元合金相图的k值
图5和图6所示分别为不同凝固模式下基金镍基二元合金相图的k值计算的雀斑数量与液相相对密度差的关系。结果发现,采用二元合金相图中的k值,拟合效果不好,其线性拟合优度R2最大时仅为0.4,液相相对密度差与雀斑数量之间的线性关系不明显。显然各元素偏析情况在高温合金与二元合金体系中有着明显的不同。
2.3.3 采用Thermo-Calc计算的k值
采用Thermo-Calc的k值计算基于平衡凝固模式下雀斑数量与液相相对密度差的关系,因此只对Lever模型进行了拟合验证,结果如图7所示。
结果显示,采用Thermo-Calc的k值,计算结果与实验结果拟合较好。在不知道实际的k值的情况下,可以用通过Thermo-Calc计算得到k值。
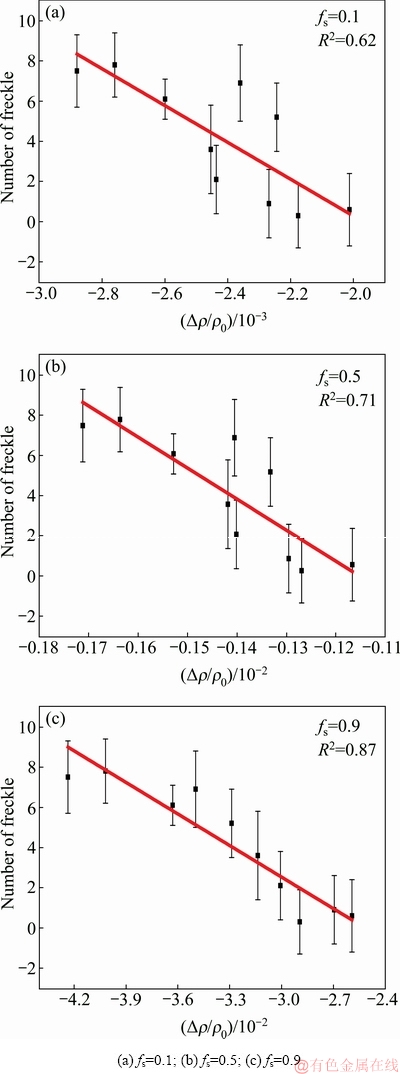
图3 Scheil模式下基于实验测得的k值计算不同凝固分数下雀斑数量与液相相对密度差的拟合情况
Fig. 3 Fitting curves between number of freckles and relative liquid densities using k values of experiment at different solidification fractions by Scheil model

图4 Lever模式下基于实验测得的k值计算不同凝固分数下雀斑数量与液相相对密度差的拟合情况
Fig. 4 Fitting curves between number of freckles and relative liquid densities using k values of experiment in different solidification fractions by Lever model
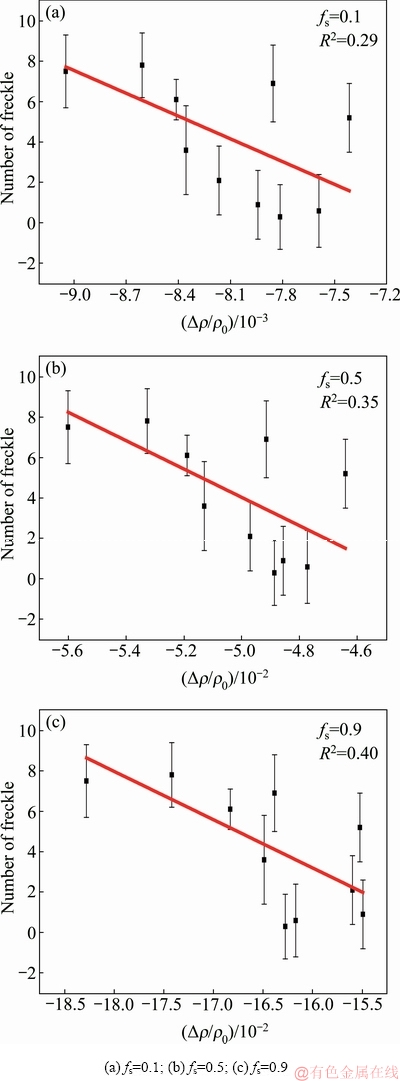
图5 Scheil模式下基于镍基二元合金相图中的k值计算不同凝固分数下雀斑数量与液相相对密度差的拟合情况
Fig. 5 Fitting curves between number of freckles and relative liquid densities using k values based on Ni-based binary phase diagram at different solidification fractions by Scheil model

图6 Lever模式下基于镍基二元合金相图中的k值计算不同凝固分数下雀斑数量与液相相对密度差的拟合情况
Fig. 6 Fitting between number of freckles and the relative liquid densities using k values based on Ni-based binary phase diagram at different solidification fractions by Lever model
表5 各元素在不同凝固分数下P值大小
Table 5 P value of each element at different solidification fraction


图7 Lever模式下采用Thermo-Calc计算不同凝固分数下雀斑数量与液相相对密度差的拟合情况
Fig. 7 Fitting curves between number of freckles and relative liquid densities using Thermo-Calc in different solidification fractions
表5所示为采用Thermo-Calc计算的k值时各元素的P值大小。Al、Re、Ta、Hf、 W等元素对雀斑的影响作用较其他元素显著。Al、Re、W元素的P值为负,对雀斑产生有促进作用,而Ta、Hf元素的P值为正,对雀斑产生有抑制作用,其他元素的P值接近0,抑制或促进作用不显著。同时,在不同凝固时刻,元素对雀斑的影响力也不同。凝固初期(fs=0.1)时,Ta、Hf、Al、Re的P值接近,他们对雀斑的影响作用相差不大;但是随着fs的增加,Ta、Hf的P值显著增加,对雀斑的抑制作用大幅度提高。凝固初期各元素对雀斑的影响大小:Re>Hf>Al、Ta>W;凝固后期各元素对雀斑的影响大小:Hf>Ta>Re、Al、W。总体上来看,对SX系列合金,单位含量的Hf元素对雀斑有最强的抑制作用,Ta元素抑制作用次之;Al、Re对雀斑有较强的促进作用,W次之。
3 结论
1) 定义了一个元素的雀斑形成倾向因子P,用来表征各单位含量的元素对雀斑形成倾向大小。其值主要与密度溶质膨胀系数β、密度温度膨胀系数βT、平衡分配系数k、液相线斜率m及选取的凝固模型有关。若P>0,则表示该元素的添加会抑制雀斑的形成,反之P<0,则促进雀斑形成。P的绝对值大小代表该抑制或促进作用的大小。
2) 给出了β和βT的计算计算公式,对SX系列合金的计算结果表明,溶质偏析对液相密度的影响远远大于温度梯度对其的影响,在对P值计算的时候,可以略去mβT这一项。对SX系列合金来说,其各元素的β值如下:βAl=-0.022,βCr=-0.0024,βCo=0.00018,βRe=0.0055,βTa=0.0045,βHf=0.0033,βW=0.0052,βMo= 0.0015。
3) 3种不同来源的k值被代入该模型计算,验证了模型的准确性。结果表明,基于二元合金相图的k值,预测结果与实验结果拟合较差,其线性拟合优度R2最大时仅为0.4;而采用实验和Thermo-Calc的k值,拟合较好,R2最大值分别达到0.87和0.95。
4) 计算了SX系列合金的P值,结果显示,单位含量下的Hf元素雀斑抑制作用最强,Ta元素次之;Al、Re对雀斑有较强促进作用,W次之。
5) 该模型能够预测不同组分合金和雀斑形成之间影响规律,完善了目前雀斑判据在合金成分上的不足,有助于帮助我们合理设计合金成分,提高合金固有的抗雀斑能力。
REFERENCES
[1] 高斯峰, 刘 林, 胡小武, 葛丙明, 张 军, 傅恒志. 镍基高温合金定向凝固过程中雀斑缺陷研究进展[J]. 材料科学与工程学报, 2010, 28(1): 145-151.
GAO Si-feng, LIU Lin, HU Xiao-wu, GE Bing-ming, ZHANG Jun, FU Heng-zhi. Review of freckle defects under directional solidification of nickle-based superalloys[J]. Journal of Materials Science & Engineering, 2010, 28(1): 145-151.
[2] 赵新宝, 刘 林, 杨初斌, 张 军, 李玉龙, 傅恒志. 镍基单晶高温合金凝固缺陷研究进展[J]. 材料工程, 2012(1): 93-98.
ZHAO Xin-bao, LIU Lin, YANG Chu-bin, ZHANG Jun, LI Yu-long, FU Heng-zhi. Advance in research of casting defects of directionally solidified nickel-based single superalloys[J]. Journal of Materials Engineering, 2012(1): 93-98.
[3] Sarazin J R, Hellawell A. Channel formation in Pb-Sn, Pb-Sb, and Pb-Sn-Sb alloy ingots and comparison with the system NH4Cl-H2O[J]. Metallurgical & Materials Transactions A, 1988, 19(19): 1861-1871.
[4] Tewari S N, Shah R. Macrosegregation during dendritic arrayed growth of hypoeutectic Pb-Sn alloys: Influence of primary arm spacing and mushy zone length[J]. Metallurgical & Materials Transactions A, 1996, 27(5): 1353-1362.
[5] Beckermann C, Gu J P, Boettinger W J. Development of a freckle predictor via, rayleigh number method for single-crystal nickel-base superalloy castings[J]. Metallurgical & Materials Transactions A, 2000, 31(10): 2545-2557.
[6] Yang W, Chang K M, Chen W. Freckle criteria for the upward directional solidification of alloys[J]. Metallurgical & Materials Transactions A, 2001, 32(2): 397-406.
[7] 张麦仓, 曹国鑫, 董建新. 冷却速度对 GH4169 合金凝固过程微观偏析及糊状区稳定性的影响[J]. 中国有色金属学报, 2013, 23(11): 3107-3113.
ZHANG Mai-cang, CAO Guo-xin, DONG Jian-xin. Effect of cooling rate on microsegregation behaviors and mush zone stability of GH4169 alloy during solidification process [J]. The Chinese Journal of Nonferrous Metals, 2013, 23(11): 3107-3113.
[8] Pollock T M, Murphy W H. The breakdown of single-crystal solidification in high refractory nickel-base alloys[J]. Metallurgical & Materials Transactions A, 1996, 27(4): 1081-1094.
[9] Long Z, Liu X, Yang W. Thermodynamic assessment of liquid composition change during solidification and its effect on freckle formation in superalloys[J]. Materials Science & Engineering A, 2004, 386(1/2): 254-261.
[10] 王 玲, 蔡文静, 刘 林. In718合金凝固过程中偏析和二次枝晶角度对糊状区 Rayleigh 数的影响[J]. 铸造技术, 2012, 33(10): 1191-1193.
WANG Ling, CAI Wenjing, LIU Lin. Effects of segregation of Nb, Mo and orientation of secondary dendrites on Rayleigh number in mushy zone of Ni-base superalloys[J]. Foundry Technology, 2012, 33(10): 1191-1193.
[11] 封少波, 张楠楠, 罗兴宏. 偏析对 DZ483镍基高温合金糊状区内液相密度的影响[J]. 金属学报, 2012, 48(5): 541- 546.
FENG Shao-bo, ZHANG Nan-nan, LUO Xing-hong. Influence of segregation on liquid density in the mushy zone of DZ483 Ni-based superalloy[J]. Acta Metallurgica Sinica, 2012, 48(5): 541-546.
[12] Tin S, Pollock T M. Stabilization of thermosolutal convective instabilities in Ni-based single-crystal superalloys: Carbide precipitation and rayleigh numbers[J]. Metallurgical & Materials Transactions A, 2003, 34(9): 1953-1967.
[13] YUAN L, LEE P D. A new mechanism for freckle initiation based on microstructural level simulation[J]. Acta Materialia, 2012, 60(12): 4917-4926.
[14] AMOUYAL Y, SEIDMAN D N. The role of hafnium in the formation of misoriented defects in Ni-based superalloys: An atom-probe tomographic study[J]. Acta Materialia, 2011, 59(9): 3321-3333.
[15] Iida T, Guthrie R I. The physical properties of liquid metals[M]. Oxford: Clarendon Press, 1988.
[16] Mcdonald R J, Hunt J D. Convective fluid motion within the interdendritic liquid of a casting[J]. Metallurgical Transactions, 1970, 1(6): 1787-1788.
[17] Magirl C S, Incropera F P. Flow and morphological conditions associated with unidirectional solidification of aqueous ammonium chloride[J]. Journal of Heat Transfer, 1993, 115(4): 1036-1043.
[18] Auburtin P, Cockcroft S L, Mitchell A. Liquid density inversions during the solidification of superalloys and their relationship to freckle formation in castings[J]. Superalloys 1996, 1996: 443-447.
[19] Ma D X, Zhou B, Bührig-Polaczek A. Investigation of freckle formation under various solidification conditions [C]//Advanced Materials Research. Trans Tech Publications, 2011, 278: 428-433.
[20] 戴永年. 二元合金相图集[M]. 北京: 科学出版社, 2009.
DAI Yong-nian. Binary alloy phase diagrams[M]. Beijing: Science Press, 2009.
Modeling of constituent-based freckle predictor for nickel-base superalloys
BAO Chao-jun1, LI Zhen-feng2, LIU feng1, JIANG Liang1
(1. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China;
2. Zhuzhou AVIC Power Investment Casting Co., Ltd., Zhuzhou 412000, China)
Abstract: Aiming at the currently shortage of the freckle criterion in the alloy constituents, a constituent-based freckle predictor for nickel-base suppalloy was modeled and verified by the experiment data. The effect of each element on the liquid density was quantitatively analyzed by calculating the solutal expansion coefficient β and the thermal expansion coefficient βT of each element. The impact of each element was quantified by defining a freckle formation tendency factor. Based on calculations of these variables, a constituent-based freckle predictor was modeled, which can predict the influence between different alloy constituents and freckle formation. Three different equilibrium distribution coefficients k were taken into this model and verified which was the best k value to predict freckle. The results show that the fitting of the number of freckles using the k value based on binary phase diagram is poor, and the linear goodness-of-fit (R2) maximum is only 0.4; while using the k values of experiment and Thermo-Calc the fitting is good, and the maximum R2 reach 0.87 and 0.95, respectively. Finally, the P values were calculated for the SX alloys, and the results show that the hafnium has the strongest influence on freckle prevention, tantalum also has beneficial effects though not as pronounced as hafnium; aluminum and rhenium have the stronger promoting effect on freckles, and tungsten is the second.
Key words: freckle; superalloy; constituent; freckle formation tendency factor; equilibrium distribution coefficient; prediction model
Foundation item: Project(621020093) supported by the Independent Innovation Project of State Key Laboratory of Powder Metallurgy, China
Received date: 2018-02-20; Accepted date: 2018-12-20
Corresponding author: LIU Feng; Tel: +86-18670324887; E-mail: liufengehe@163.com
(编辑 龙怀中)
基金项目:粉末冶金国家重点实验室自主创新课题(621020093)
收稿日期:2018-02-20;修订日期:2018-12-20
通信作者:刘 锋,副教授,博士;电话:18670324887;E-mail:liufengehe@163.com