J. Cent. South Univ. Technol. (2010) 17: 1230-1237
DOI: 10.1007/s11771-010-0624-z
Levitation mechanism modelling for maglev transportation system
ZHOU Hai-bo(周海波), DUAN Ji-an(段吉安)
School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2010
Abstract: A novel maglev transportation system was proposed for large travel range ultra precision motion. The system consists of a levitation subsystem and a propulsion subsystem. During the propulsion subsystem driving the moving platform along the guideway, the levitation subsystem uses six pairs of electromagnets to steadily suspend the moving platform over the guideway. The model of the levitation system, which is a typical nonlinear multi-input multi-output coupling system and has many inner nonlinear coupling characteristics, was deduced. For testifying the model, the levitation mechanism was firstly controlled by proportional- integral-differential (PID) control, and then a lot of input-output data were collected for model parameter identification. The least-square parameter identification method was used. The identification results prove that the model is feasible and suitable for the real system.
Key words: maglev transportation system; levitation mechanism; modeling; parameters identification
1 Introduction
Magnetic levitation technology is contact-free and wear-free, and hence has many advantages over traditional moving mechanisms. It is widely used in various fields such as high-speed maglev trains and frictionless bearings [1-2]. Maglev transportation system, which employs magnetic levitation mechanisms and magnetic linear propulsion motors, has the potential to achieve ultra-precision and high-speed motion of an object. It is widely accepted as a feasible choice when developing ultra-precision positioning mechanisms, and many maglev transportation systems also have been developed in recent years. For instance, WAI and LEE [3] developed a maglev transportation system to provide large-range linear motion. But its precision and stiffness performances are not very good. KIM et al [4] designed a high precision magnetic levitation stage with capability of planar motion for photolithography in semiconductor manufacturing, and KUO et al [5-6] developed an ultra- precision x-y-θ motion magnetic suspension stage. Though their precision is high, the moving range is short. These platforms have no ability to provide ultra- precision linear positioning motion with travel range.
Maglev transportation system is a complicated nonlinear multi-input multi-output (MIMO) coupling system. Many factors may influence the control performance. Firstly, the electromagnet has many inner strong nonlinear characteristics such as hysteresis, magnetism saturation and parameters variation. Secondly, the air gaps of ultra precision magnetic-suspension system either remain constant or very small variations, which makes the control and modeling very difficult. Thirdly, the magnetic suspension system is a typical open-loop unstable system. And to steadily suspend the moving platform over the guideway, many pairs of electromagnets are required to work together, but strong coupling effects exist among these electromagnets. Therefore, modeling and controlling well the maglev system are very difficult and important for realizing ultra precision motion.
In this work, a novel maglev transportation system was constructed for realizing large travel range ultra- precision high-speed linear motion. The present maglev transportation system consisted of a levitation subsystem and a propulsion subsystem. In the levitation mechanism, six pairs of electromagnets were used to suspend the moving platform. A differential electromagnet driving mode was employed to provide suspension force, which has better stiffness and strength than that of the single electromagnet driving mode. Accordingly, its modeling and control were also different from the traditional driving mode. Since the moving performance of the maglev transportation system was up to the levitation mechanism, the model of the levitation mechanism was then built. To testify the model, closed-loop system identification method was adopted for the PID controllers controlled levitation subsystem. The testified model will certainly provide great help for the subsequent controller design.
2 Structure of maglev transportation system
Fig.1 illustrates the overall framework of the proposed maglev transportation system. The maglev system consists of a fixed basal platform and a moving platform. These two parts are supposed to be contact-free when the system runs. From their utility, the maglev transportation system can also be divided into two mechanisms: levitation mechanism and propulsion mechanism. The levitation mechanism contains all electromagnets, gap sensors and moving platform in Fig.1, which is used to steadily suspend the moving platform over the guideway. The propulsion mechanism is employed to drive the moving platform along the guideway (e.g., axis x) after the moving platform is suspended, which is formed by moving part of linear motor, fixed part of linear motor, grating scale, guideway and fender.
Fig.2 shows the structural drawing of the levitation mechanism. In the levitation mechanism, there are 12 equal-size cubic electromagnetic actuators (e.g., electromagnet pair 1, electromagnet pair 2, and so on) being symmetrically fixed on the moving platform. Taking electromagnet pair 1 as an example, the upper electromagnet generates force to pull down the moving platform, while the lower one pulls up the moving platform. The difference of magnetism is used to counteract the mass of moving platform. This driving mode is called as differential mode (short for differential electromagnet driving mode). Whereas, the traditional driving mode adopts only the lower electromagnet. The differential mode has many advantages over the traditional one. The most obvious one is that the differential mode brings higher stiffness and strength to the moving platform [1]. These electromagnets work together to steadily suspend the moving platform. There are six gap sensors being armed near the electromagnet pairs to real-time feedback the distances between electromagnets and guideway surfaces.
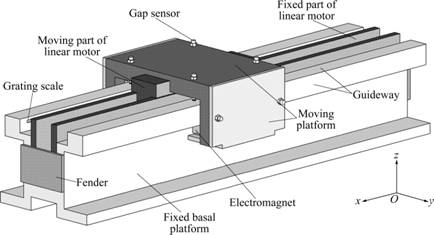
Fig.1 Framework of proposed maglev transportation system
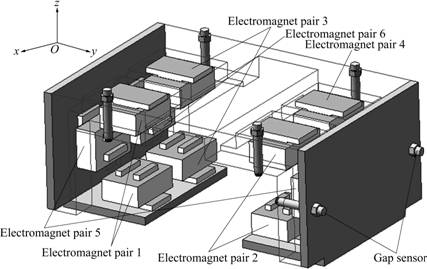
Fig.2 Structural drawing of levitation mechanism
In the propulsion subsystem, the fixed part and moving part of linear motor are contact-free. The former is mounted on the fixed basal platform, and the latter is embedded into the moving platform. The magnetism between the two parts drives the moving platform. The grating scale is used to test the position of moving platform for controlling. Two fenders are placed at the end of guideway to avoid digression.
For every pair of electromagnet, a differential direct current (DC) control method was used to control the electromagnet force. Fig.3 depicts the detailed control sketch of one electromagnet pair, where I0 represents the bias current; i0 represents the current used to counteract the mass of moving platform (accordingly, i0=0 for electromagnet pairs 5 and 6); zt represents the distance between surfaces of gap sensor and lower electromagnet; zg represents the thickness of the fixed guideway; ze represents the goal position of moving platform; and z0 represents the distance between surfaces of gap sensor and upper electromagnet. I0, i0, zt, zg and z0 are all fixed variables for every pair of electromagnets once all electromagnets are built. It is obvious that the real-time feedback value of gap sensors is time-varying, so ?z is used to define the variation. Accordingly, ?i denotes the variation of controller output. ?i can be adjusted by controller according to the position information got from gap sensors. This will then result in varying magnetic force exerting on moving platform along axes z and y. For I0 is far bigger than i0 and ?i when the system steadily runs, the setting of bias current can greatly improve the stiffness and strength of suspension force. Two power amplifiers are used to amplify the tiny control signal of the controller output to a real current in the coils of electromagnets. Their amplify scale is designed to be 1.
3 Modeling of levitation mechanism
The maglev transportation system is a typical nonlinear multi-input multi-output coupling system and the levitation mechanism is the most important part. The moving platform was assumed to be rigid body and simplified to be cubic body (nominal moving platform) shown in Fig.4, where lt, wt, and ht represent the total length, width and height of the nominal moving platform, respectively; fi (i=1, …, 6) denotes the net force of electromagnet pair i; ll represents the horizontal distance between f1 (f2, f5) and f3 (f4, f6); and lw represents length between f1 (f3) and f2 (f4). The mass density of the moving platform is assumed to be uniform everywhere. This means that the body’s centroid coincides with the geometrical center of the plate, which is the origin of axes xp and yp shown in Fig.4. The origin of maglev system’s Cartesian coordinates (x y z) is supposed to be located at the top surface of guideway. Being rigid, the nominal moving platform does not bend in any direction.
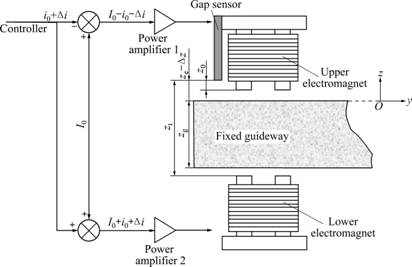
Fig.3 Control sketch of one electromagnet pair
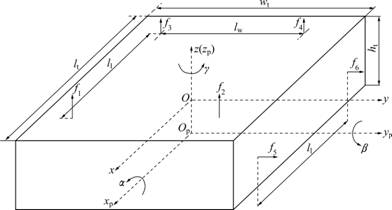
Fig.4 Sketch diagram of moving platform
When the maglev system runs steadily, six degrees-of-freedom (DOF) could be considered in a fully suspended substance. Except the propulsion motion of linear motor along axis x, there are other five DOFs being affected by levitation mechanism. They are linear motions along axes y and z, rotating motion α, β and γ around axes x, y and z, respectively.
In general, the magnet suspension force of a single electromagnet can be expressed as [7]:
 (1)
(1)
where i represents control current in the coil; c represents the distance between electromagnet and iron guideway; A represents sectional area of the electromagnet; N represents coil loop circle number of the electromagnet; and μ0 represents magnetic conductivity in the air. For the proposed maglev system of Fig.3, it is obvious that the net force of six electromagnet pairs bear as follows:
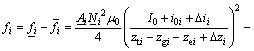
 (2)
(2)
where subscript i=1, …, 6; Δii represents the variation of control current of the ith electromagnet pair; all overbar and underbar denote the terms of upper and lower electromagnet of six pairs of electromagnets, respectively. Linearizing Eq.(2) at their origin (e.g., ?ii=0 and ?zi=0), the following linear force model is achieved:
fi=
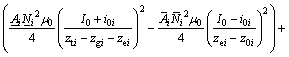
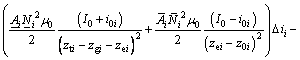
 (3)
(3)
To describe simply, in the following content fi=ki1+ ki2?ii-ki3?zi was used to replace Eq.(3). For the nominal moving platform in Fig.4, with mathematical manipulations, kinetic energy Ek and potential energy Ep [8] of the moving platform can be represented as
 (4)
(4)
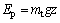 (5)
(5)
where mt represents the total mass of the moving platform; g represents the acceleration due to gravity [9]. Jx=mtwt2/12, Jy=mtlt2/12, and Jz=mt(wt2+lt2)/12 represent the inertia with respect to axes x, y and z, respectively. According to Lagrangian method, define the Lagrangian function L [3, 10] as follows:
L=Ek-Ep (6)
So the Lagrangian equations of the moving platform are [11]
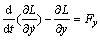 (7)
(7)
 (8)
(8)
 (9)
(9)
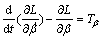 (10)
(10)
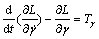 (11)
(11)
where Fy and Fz represent nominal control forces of nominal moving platform in the direction along axes y and z; Tα, Tβ and Tγ are nominal control effects of DOF α, β and γ, respectively. While
 (12)
(12)
 (13)
(13)
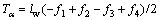 (14)
(14)
 (15)
(15)
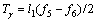 (16)
(16)
Combining Eqs.(7)-(16), the dynamic model of moving platform is as follows:
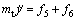 (17)
(17)
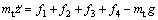 (18)
(18)
 (19)
(19)
 (20)
(20)
 (21)
(21)
Since the actual levitation status that is detected from gap sensors is six gap values between six electromagnets and the iron guideway, there are following relations to realize the transfer between gap values (ze1+?z1, ze2+?z2, ze3+?z3, ze4+?z4, ze5+?z5, ze6+ ?z6) and system states (y, z, α, β, γ):
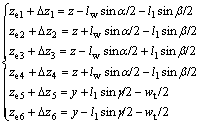 (22)
(22)
Because the maximum gap was proposed to be near 1 mm, whereas the width, length and height of the moving platform were far larger than 10 mm, therefore, 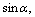
 and
and  were far less than 0.1, and it is reasonable to assume that
were far less than 0.1, and it is reasonable to assume that
 and
and  . Rewrite Eq.(22) as follows:
. Rewrite Eq.(22) as follows:
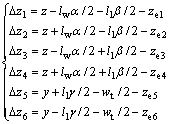 (23)
(23)
Combining Eqs.(3), (17)-(21) and (23), the model of levitation mechanism is achieved as
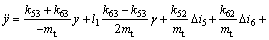
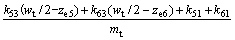 (24)
(24)
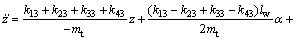
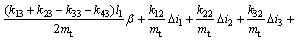
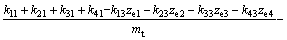
 (25)
(25)
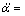
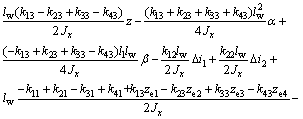
 (26)
(26)
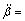
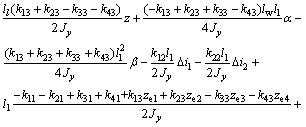
 (27)
(27)
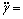
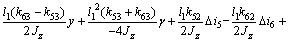
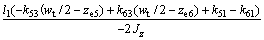 (28)
(28)
After mathematical manipulations, the dynamic model of the levitation system can be represented as follows:
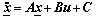 (29)
(29)
where  represents the system output vector; control current vector u=[?i1, ?i2, ?i3, ?i4, ?i5, ?i6] represents the system input;
represents the system output vector; control current vector u=[?i1, ?i2, ?i3, ?i4, ?i5, ?i6] represents the system input;
 ;
;
 ; and
; and
C=[a30 a31 a32 a33 a34]T are constant matrices, a1 to a34 can be extracted from Eqs.(24)-(28).
4 Model parameters identification and experimental results
To testify the model, it is necessary to identify the unknown parameters in the deduced model (29). From Eqs.(3) and (24)-(29), there are at least 34 parameters in matrices A, B and C to be identified.
Maglev system is obviously open-loop unstable, therefore, closed-loop system identification method was adopted [12]. As a typical and useful parameters identification method, least-square method with variable forgetting factors (LSVFF) was chosen for the MIMO levitation system [13-14].
For the closed-loop identification, firstly, six proportional-integral-differential (PID) controllers were designed for six pairs of electromagnets (e.g., f1 to f6) to realize the steady suspension of the levitation system. The control objective for these PID controllers was to roughly keep all the statuses at a user-specified zd=[ze1, ze2, ze3, ze4, ze5, ze6]T by adjusting magnetic forces fi to counteract the weight of the moving and the disturbances. Fig.5 shows the PID control diagram of levitation system. In Fig.5, the six simple controllers are used to independently control six pairs of electromagnets without considering the strong coupling among channels.
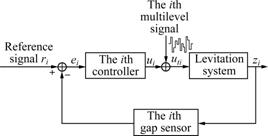
Fig.5 PID control diagram of levitation system
After the system achieves rough steady running, six multilevel signals were added into six inputs of moving platform (e.g., outputs of six PID controllers) to actuate all mode in the levitation system. Random noise was chosen as multilevel signal, and its breadth and repeated frequency were adjusted in order to make the six moving platform outputs fully cover their output ranges. The step interval is h=0.000 5 s. Some pieces of input and output data are plotted in Fig.6. The real ranges of gap sensors were designed to be within [0.1, 1.2] mm, and the gap values in Fig.6 obviously cover their whole output range.
In the parameter identification, 31 000 pairs of input-output data were collected with sample time ts=0.000 5 s. Every pair of data contain six input variables and six output variables of the platform (e.g.,  and zi(k) in Fig.5) at specific sample time. And 30 000 pairs of them were used to identify 34 unknown parameters in the following differential equations of model (29) [14]:
and zi(k) in Fig.5) at specific sample time. And 30 000 pairs of them were used to identify 34 unknown parameters in the following differential equations of model (29) [14]:
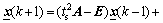
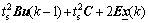 (30)
(30)
where E represents identity matrix and the differential equation was got by transferring (29) with equation
 The LSVFF, which
The LSVFF, which
is a typical parameter identification method and widely used in many literatures [14-15], was used to identify the parameters. After parameter identification, all 34 parameters in Eq.(30) have good convergence. Four of them were randomly picked out and plotted in Fig.7. The convergence curves of other 30 parameters have similar shape and good convergence performance.
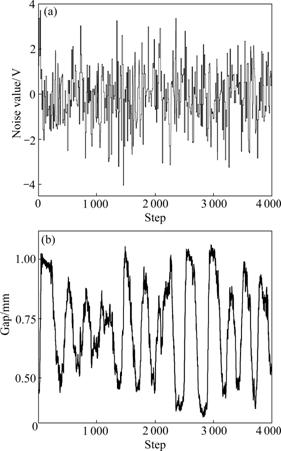
Fig.6 Multilevel signal and the corresponding output for electromagnet pair 1: (a) Noise value; (b) Gap
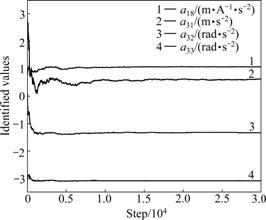
Fig.7 Identification results of four selected parameters
By using measurement and estimation, the values of all parameters in Eqs.(3) and (24)-(28) were approximately chosen. For comparison, the estimated range, the initial values and the identified values of all parameters are listed in Table 1. From Table 1, it is obvious that all parameters are in their ranges. Other 1 000 pairs of input-output data were used to test the following identified system:
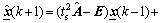
 (31)
(31)
where 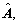
 and
and  represent the identified values of A, B and C, respectively; and
represent the identified values of A, B and C, respectively; and 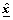 represents the estimated values. In the test results, the estimated output
represents the estimated values. In the test results, the estimated output 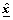 is very close to the real output x. Two of them are plotted in Fig.8. The results show that the identified values are almost suitable for the real ones. Eq.(29) is a available model of the maglev transportation system.
is very close to the real output x. Two of them are plotted in Fig.8. The results show that the identified values are almost suitable for the real ones. Eq.(29) is a available model of the maglev transportation system.
Table 1 Estimated, initial and identified values of all parameters

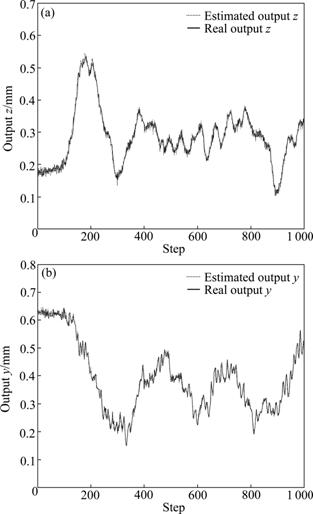
Fig.8 Identified results for outputs z and y: (a) Output z; (b) Output y
5 Conclusions
(1) A novel maglev transportation system is proposed for providing large travel range ultra precision motion, which has better stiffness and strength.
(2) The dynamic model of the key subsystem in maglev transportation system is built.
(3) The dynamic model is testified by the least- square parameter identification method. The model fits the real platform well. The presented modeling method and model itself are feasible and will provide a useful guidance in the subsequent controller design and real application.
References
[1] JING Ming-qing, LIU Heng, LIAN Jin-xing, YU Lie. Two-dimensional high precision positioning maglev stage [J]. Journal of Xi’an Jiao Tong University, 2008, 42(11): 1377-1381. (in Chinese)
[2] KALOUST J, HAM C, SIEHLING J, JONGEKRYG E, HAN Q. Nonlinear robust control design for levitation and propulsion of a maglev system [J]. IEE Proceedings—Control Theory Applications, 2004, 151(4): 460-464.
[3] WAI R J, LEE J D. Adaptive fuzzy-neural-network control for maglev transportation system [J]. IEEE Trans on Neural Networks, 2008, 19(1): 54-70.
[4] KIM W J, TRUMPER D L, LANG J H. Modeling and vector control of planar magnetic levitator [J]. IEEE Trans on Ind Applicat, 1998, 34(6): 1254-1262.
[5] KUO S K, SHAN Xi-min, MENQ C H. Large travel ultra precision x-y-θ motion control of a magnetic-suspension stage [J]. ASME Trans on Mechatronics, 2003, 8(3): 334-341.
[6] SHAN Xi-min, KUO S K, ZHANG Ji-hua, MENQ C H. Ultra precision motion control of a multiple degrees of freedom magnetic suspension stage [J]. ASME Trans on Mechatronics, 2002, 7(1): 67-78.
[7] SINHA P K, PECHEV A N. Model reference adaptive control of a maglev system with stable maximum descent criterion [J]. Automatica, 1999, 35(8): 1457-1465.
[8] LI Qun-ming, GAO Dan, DENG Hua, OUYANG Hua. Modal analysis of a high-precision magnetic suspension stage [C]// Proceedings of the 7th World Congress on Intelligent and Automation. Chongqing: IEEE, 2008: 6044-6048.
[9] ZHENG Xiao-jing, WU Jian-jun, ZHOU You-he. Numerical analysis on dynamic control of five-degree-of-freedom maglev vehicle moving on flexible guideways [J]. Journal of Sound and Vibration, 2000, 235(1): 43-61.
[10] LI Qun-ming, WAN Liang, ZHU Ling, XU Zhen. Decoupling control for a magnetic suspension stage [C]// IEEE International Conference on Control and Automation. Guangzhou: IEEE, 2007: 323-328.
[11] BOEIJ J D, STEINBUCH M, GUTIERREZ H M. Mathematical model of the 5-DOF sled dynamics of an electrodynamic maglev system with a passive sled [J]. IEEE Transactions on Magnetics, 2005, 41(1): 460-465.
[12] LI Han-xiong, DENG Hua. An approximate internal model-based neural control for unknown nonlinear discrete processes [J]. IEEE Transactions on Neural Networks, 2006, 17(3): 659-670.
[13] DING Feng, CHEN Tong-wen. Performance bounds of forgetting factor least-squares algorithms for time-varying systems with finite measurement data [J]. IEEE Transactions on Circuits and Systems Ⅰ: Regular Papers, 2005, 52(3): 555-566.
[14] LJUNG L. System identification: Theory for the user [M]. 2nd ed. Beijing: Tsinghua University Press, 2002: 10-260.
[15] PALEOLOGU C, BENESTY J, CIOCHINA S. A robust variable forgetting factor recursive least-squares algorithm for system identification [J]. IEEE Signal Processing Letters, 2008, 15: 597- 600.
(Edited by LIU Hua-sen)
Foundation item: Projects(50735007, 51005253) supported by the National Natural Science Foundation of China; Project(2007AA04Z344) supported by the National High-Tech Research and Development Program of China
Received date: 2010-03-27; Accepted date: 2010-06-28
Corresponding author: DUAN Ji-an, PhD, Professor; Tel: +86-731-88836858; E-mail: duanjian@mail.csu.edu.cn