J. Cent. South Univ. Technol. (2007)03-0399-05

DOI: 10.1007/s11771-007-0078-0               

Improved sample filtering method for measuring end-to-end path capacity

LI Wen-wei(黎文伟)¹, TANG Jun-long(唐俊龙)², ZHANG Da-fang(张大方)¹, XIE Gao-gang(谢高岗)³

(1. School of Software, Hunan University, Changsha 410082, China;

2. Department of Physics and Electronic Science, Changsha University of Science and Technology,

Changsha 410082, China;

3. Institute of Computing Technology, Chinese Academy of Sciences, Beijing 100080, China)

Abstract: By analyzing the effect of cross traffic (CT) enforced on packet delay, an improved path capacity measurement method, pcapminp algorithm, was proposed. With this method, path capacity was measured by filtering probe samples based on measured minimum packet-pair delay. The measurability of minimum packet-pair delay was also analyzed by simulation. The results show that, when comparing with pathrate, if the CT load is light, both pcapminp and pathrate have similar accuracy; but in the case of heavy CT load, pcapminp is more accurate than Pathrate. When CT load reaches 90%, pcapminp algorithm has only 5% measurement error, which is 10% lower than that of pathrate algorithm. At any CT load levels, the probe cost of pcapminp algorithm is two magnitudes smaller than that of pathrate, and the measurement duration is one magnitude shorter than that of pathrate algorithm.

Key words: network measurement; path capacity; capacity measurement; path delay

1 Introduction

Measuring the capacity of an end-to-end Internet path is a crucial operation for many network activities. With knowledge of the capacity of end-to-end paths in mind, ISPs can locate network bottlenecks, for optimized capacity planning and bandwidth allocation, and multimedia applications can select appropriate servers. Moreover, the recent research in overlay networks and application layer multicast can also benefit from such capacity information in better structuring their overlays and trees.

For measuring the capacity, a series of probing packets with specific pattern should be sent into the target path. Guaranteeing the estimation accuracy is a fundamental requirement for any path capacity measurement algorithms or tools. Furthermore, because the capacity measurement activity may be adopted widely, it also requires the algorithms or tools to keep minor probe costs and have minor probe duration, for practical applicable.

Starting with fulfill all or part of these requirements, a lot of tools have been developed in the community^[1-7]. However, these tools are far away for practical utilizations, as they have either poor estimation precision or too large probing costs^[8]. According to the probing techniques adopted, these tools can be divided into two categories: variable packet size(VPS) method and packet pair/train dispersion(PPTD) method^[9]. Tools such as pathchar^[1], clink^[1] and nettimer^[2], are based on VPS method. VPS method may yield significant capacity underestimation errors if the measured path includes store-and-forward layer-2 devices^[10], which makes it not practical for path capacity measurement. Consequently, the current improvements of capacity measurement are focused on PPTD method.

The PPTD technique was originally proposed by JACOBSON^[11] for congestion control, then much work has been done to improve it, and it was adopted for measuring delay variation^[12] and path capacity^[3-7]. In PPTD technique, the source sends multiple packet pairs to the receiver. Each packet pair consists of two packets of the same size sent back to back. The path capacity is estimated by observing the difference of the two packets’ receiving time at the receiver. The main challenge in PPTD technique is to find a robust statistical technique that can extract an accurate capacity estimate from noisy measurements. COSTANTINOS et al^[7] introduced the most accurate capacity estimation tool currently available: pathrate. However, pathrate needs too large probing cost and too long probing duration for estimation, and if the network has heavy load, it also has large estimation errors.

In this paper, after analyzing the effects of cross traffic on the delays of probing packet pair, a minimum delay based samples filtering method for path capacity measurement was proposed. The measurability of minimum packet pair delays was also analyzed by simulation. The results show that this method is very accurate and has less measurement costs and durations.

2 improved sample filtering method

2.1 Principle of PPTD technique

An end-to-end network path can be viewed as a sequence of first-come first-served (FCFS) store and forward links that transfer packets from the sender to the receiver. Assuming that the path is fixed and unique for the duration of the measurements, i.e., no routing change or multipath forwarding occurs. Each link transmits data with a constant rate of bits per second, referred to link capacity or transmission rate. The path capacity is the minimum transmission rate among all links in the path. Noting that the capacity does not depend on the traffic load of the path.

Formally, if H is the number of hops (links) in the end-to-end path, C_i is the capacity of link i, and C₀ is the transmission rate of the sender, then the path capacity is

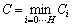              (1)

Denoting the packet pair with the same size L in measurement as PP, P₁ is the first packet in it, and P₂ is the second packet. The dispersion of a packet pair, Δt, at a specific link of the path is the time distance between the last bits of each packet. Fig.1 shows the principle of PPTD technique. Assuming that the link does not carry other traffic when a packet pair goes through it. If a link of capacity C₀ connects the source to the path and the probing packets are of size L, the dispersion of the packet pair at that first link is Δt₀=L/C₀. In general, if the dispersion prior to a link of capacity C_i is Δt_in, the dispersion after the link will be

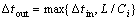          (2)

After a packet pair goes through each link along an otherwise empty path, the dispersion Δt_R measured by the receiver is

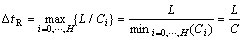    (3)

where  C is the end-to-end capacity of the path. Thus, the receiver can estimate the path capacity from C=L/Δt_R.

Admittedly, the assumption that the path is empty of any other traffic (referred as cross traffic) is far from reality. Even worse, cross traffic can either increase or decrease the dispersion Δt_R, causing underestimation or overestimation, respectively, of the path capacity. Capacity underestimation occurs if cross traffic packets are transmitted between the probing packet pair at a specific link, increasing the dispersion to more than L/C. Capacity overestimation occurs if cross traffic delays the first probe packet of a packet pair more than the second packet at a link that follows the path’s narrow link. Thus a robust sample filtering method is important for capacity measurement.

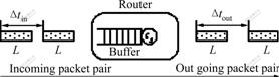
Fig.1 Principle of PP technique

2.2 Analysis of packet pair delay under cross traffic

The end-to-end delay of a probe packet is the sum of the time that needs to go through each link along the path. The packet delay at each hop consists of four components: the propagating time of electronic or photic signals, d_p; the transmitting time of bits, d_t; the processing time of routers, d_pro; and the queuing time induced by cross traffic, d_q. Generally, the d_p, d_t and d_pro are fixed, and the d_q is related to the load of cross traffic. Denote the fixed component of packet delay as d_F, then

d_F＝d_p＋d_t＋d_pro            (4)

Consequently, the end-to-end delay of a path with H hops is

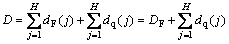 (5)

where  d_F(j) is the fixed delay of probe packet at link j,  d_q(j) is the queuing delay of it, and D_F is the sum of the fixed delay at each hop, and can be expressed as

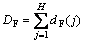          (6)

If cross traffics in the path affect the first packet P₁ in a packet pair, the delay of P₁ is determined by formula (5). If the packet P₁ is not affected by cross traffic, then the delay of it is determined by formula (6), it is the minimum delay that P₁ can probe.

Both cross traffic and P₁ affect the delay of the second packet P₂ in a packet pair. At a specific link j, denoting d_PP(j) as the queuing delay of P₂ that is caused by P₁, and denoting d_ct(j) as the queuing delay of P₂ that is caused by cross traffic, then, according to formula (5), the end-to-end delay of P₂ is

     (7)

If cross traffics in the path affect the packet P₂, the delay of it is determined by formula (7). If it is not affected by cross traffic, then the delay of it is determined by

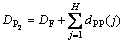         (8)

Formula (8) shows that the minimum delay P₂ can probe.

2.3 Minimum delay based filtering method

Combining formulas(5)-(8), it can be found that, the cross traffic can increase the delay of P₁ and P₂ in a packet pair. In measurement, if the packet delay of a packet pair is determined by formulas (6) and (8), it means that it is not affected by cross traffics, and then the path capacity can be calculated accurately according to formula (3). Here, in fact, is the case that both P₁ and P₂ measured the minimum delay. Thus, a minimum delay based sample filtering method for capacity measurement was proposed here.

Supposing that, n packet pairs are sent via PPTD technique in a measurement, and it collects a set of packet pair dispersion time with n samples: S₀＝{Δt₁, Δt₂,…, Δt_n}. In the same time, collect a set of packet delay with 2n samples: S＝{β₁, β₂,…, β_n}, where β₁＝(D₁(1),D₂(1)), β₂＝(D₁(2),D₂(2)),…, β_n＝(D₁(n),D₂(n)). D₁(i) is the delay of P₁ in the i-th packet pair, and D₂(i) is the delay of P₂ in the i-th packet pair.

The set S₀ is filtered with set S. Firstly, the samples are filtered with D₁(i).In set S, select samples that satisfy the condition: D₁=min{D₁(1), D₁(2),…, D₁(n)}, and they combine a subset with k samples: S′＝{γ₁, γ₂,…, γ_k}, where, γ₁＝(D₁,D₂(1)), γ₂＝(D₁,D₂(2)),…, γ_k＝(D₁(k),D₂(k)). Then, using D₂(i) to filter S′. In set S′, select samples which satisfy the condition: D₂=min{D₂(1), D₂(2),…, D₂(k)}, and they combine a subset S″ with m samples.

In fact, the set S′ only guarantees that selected samples satisfy the condition D₁=min{D₁(1), D₁(2),…, D₁(n)}, i.e., the first packet of packet pair is not queuing due to cross traffic. However, the second packet of packet pair may still suffer some queuing delay due to cross traffic, i.e., it may be D₂>min{D₂(1), D₂(2),…, D₂(n)}. Thus there still have some errors in the set S′. In the next, the filtering method is complemented to guarantee that both the first and the second packets of packet pair are not queued due to cross traffic; it is also the termination condition of the measurement algorithm.

After the set S″ is combined, complement the filtering method as follows: checking whether the samples in S″ satisfy the condition: D₂=min{D₂(1), D₂(2),…,D₂(n)}. If satisfied, then terminates measurement, and calculates path capacity with the samples in S₀ that corresponds to S″. If the condition is not satisfied, then send additional packet pairs and repeat the filtering procedure.

The network load is not very heavy at most time^[13]. To decrease the probe costs and durations of measurement, the amount of additional sent packet pairs is set to be 10, and the measurement only sends 300 packet pairs at most.

2.4 Simulation analyzing of minimum packet pair

    delay measurability

The characteristic that minimum packet delay is independent of path load has been widely used by many network applications. Current researches also have found that minimum path delay is measurable with large probability^[14]. However, these researches are focused on single packet probe. The measurability of minimum packet pair delay must be analyzed. Here, this problem was analyzed by simulation.

The topology of simulating network is shown in Fig.2. The end-to-end path consists of 6 hops. Probe packet pairs are sent from source to destination. The probe packet size is 600 byte. Under the path, there are several nodes to generate cross traffic with self-similar characteristic at different levels. The nodes at the top of the path are responsible for cross traffic reception. The packet pairs needed for measuring minimum packet pair delays under different cross traffic loads are shown in Fig.3. Even at large load, the amount of packet pair is still not very high.

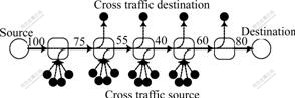
Fig.2 Topology of simulating network

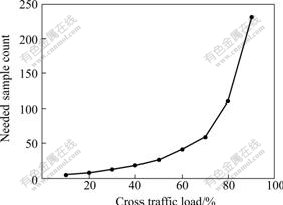
Fig.3 Samples needed for minimum packet pair delay measurement

2.5 Method implementation

The proposed method was implemented as the following steps.

1) To a specific destination host, the source host sends n probe packet-pairs with certain time interval, their delay pairs combine sample set S＝{β₁, β₂,…,β_n}, where β₁＝(D₁(1),D₂(1)), β₂＝(D₁(2), D₂(2)),…, β_n＝(D₁(n), D₂(n)).

2) Denoting D_1,min=min{D₁(1), D₁(2),…, D₁(n)}, and D_2,min=min{D₂(1), D₂(2),…, D₂(n)}.

3) In set S, search elements that satisfy the condition: D₁(i)=D_1,min, they combine sample set S′＝{γ₁, γ₂,…, γ_k}, where, γ₁＝(D₁,D₂(1)), γ₂＝(D₁,D₂(2)),…, γ_k＝(D₁(m), D₂(m)).

4) In set S′, search elements that satisfy the condition: D₂(k)= D_2,min.

5) If such elements are discovered, the path capacity is calculated as C=L/(D₂(k)-D₁(k)), and the measurement is ended.

6) Otherwise, n probe packet-pairs are sent again, and a sample set with 2n elements is built. Then, repeat from step 2.

7) After several times of repeating, if the condition in step 4 still is not satisfied, end the measurement, and calculate the path capacity as C=L/(D₂-D₁(k)), where D₂=min{ D₂(1), D₂(2),…, D₂(m)} in S′.

3 Results

To evaluate the performance of the method proposed in this paper, we implement it as a tool named pcapminp, and compare it with pathrate, the most accurate path capacity measurement tool currently available, under a small 100 Mbps IP network. The topology of the experimental network is shown in Fig.4.

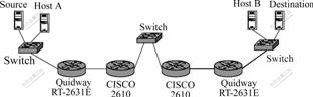
Fig.4 Topology of experimental network

3.1 Measurement accuracy

Measured path capacities of pcapminp and pathrate under different cross traffic load levels are listed in   Table 1.

When cross traffic load level is small, there is no obviously difference between the measurement errors of pcapminp and pathrate. However, pcapminp keeps a measurement error less than 2%, if the cross traffic does not exceed 40%, while pathrate has a measurement error over 2% if the cross traffic reaches 30%. When the cross traffic reaches 90%, pcapminp has only 5% error, while pathrate has 15% error. The results illustrate the method proposed is more accurate than that of pathrate.

3.2 Measurement costs and durations

The measurement costs and duration of pcapminp and pathrate under different cross traffic load levels are listed in Tables 2 and 3. As the pathrate has to generate too many packet trains to eliminate multimodal distributions of measurement, it is not strange to see from Tables 2 and 3 that pcapminp has the measurement costs and durations smaller than pathrate largely: the probe costs of pcapminp is smaller than that of pathrate with two magnitudes, and the measurement durations is shorter than that of pathrate with one magnitude.

            Table 1 Measured path capacities of pcapminp and pathrate               (Mbps)

Table 2 Probe costs of pcapminp and pathrate

             Table 3 Measurement durations of pcapminp and pathrate          (s)

4 conclusions

1) If cross traffic in the network interferes with probe packets then the probe packet will suffer additional delay; otherwise, the packets will obtain the minimum delay. Filtering the path capacity measurement samples with minimum delay will eliminate the effects of cross traffic and get accurate estimation results.

2) It can be seen from simulation that the minimum delays of probe packet pair are measurable under any cross traffic conditions. If the size of probe packet is set to be 600 byte, even at 90% cross traffic load level, the minimum delays of probe packet pair still can be measured within 231 packet pairs, which correspond to only about 270.7 kB probe costs.

3) Comparing with pathrate algorithm, the most accurate path capacity measurement tool currently available, the minimum delay based method (pcapminp) proposed is more accurate, and has less probe costs and shorter probe duration. In experiments, when cross traffic load level reaches 90%, pcapminp algorithm has only 5% measurement error, which is 10% lower than that of pathrate algorithm. Furthermore, at any cross traffic load levels, the probe costs of pcapminp algorithm is two magnitudes smaller than that of pathrate, and the measurement duration is one magnitude shorter than that of pathrate.

References

[1] DOWNEY A. Using pathchar to estimate Internet link characteristics[C]// Proceeding of the 1999 ACM SIGCOMM Conference. Cambridge: ACM Press, 1999: 241-250.

[2] LAI K, BAKER M. Measuring link bandwidths using a deterministic model of packet delay[C]// Proceeding of the 2000 ACM SIGCOMM Conference. Stockholm：ACM Press, 2000: 283-294.

[3] CARTER R, CROVELLA M. Measuring bottleneck link speed in packet-switched networks[J]. Performance Evaluation, 1996, 27(8): 297-318.

[4] LAI K, BAKER M. Measuring bandwidth[C]// Proceeding of the 18th IEEE Conference on Computer Communications (INFOCOM). New York: IEEE Press, 1999: 235-245.

[5] PAXSON V. Measurements and Analysis of End-to-End Internet Dynamics[D]. California: UC Berkeley, 1997.

[6] COSTANTINOS D, PARAMESWARAN R, DAVID M. What do packet dispersion techniques measure[C]// Proceeding of the 20th IEEE Conference on Computer Communications (INFOCOM). Anchorage: IEEE Press, 2001: 905-914.

[7] COSTANTINOS D, PARAMESWARAN R, DAVID M. Packet dispersion techniques and a capacity estimation methodology[J]. IEEE/ACM Transaction on Network, 2004, 12(6): 963-977.

[8] LEE S, SHARMA P, BANERJEE S, et al. Measuring bandwidth between PlanetLab nodes[C]// Proceeding of the 2005 Passive and Active Measurement Workshop. Boston: Springer Press, 2005: 292-305.

[9] RAVI P, CONSTANTINOS D, MARGARET M, et al. Bandwidth estimation: Metrics, measurement techniques, and tools[J]. IEEE Network, 2003, 17(6): 27-35.

[10] RAVI P, COSTANTINOS D, BRUCE A. The effect of layer- 2 store-and-forward devices on per-hop capacity estimation[C]// Proceeding of the 22nd IEEE Conference on Computer Communications (INFOCOM). San Francisco: IEEE Press, 2003: 2090-2100.

[11] JACOBSON V. Congestion avoidance and control[J]. ACM Computer Communication Review, 1988, 18(4): 314-329.

[12] LI W W, WANG J F, XIE G G, et al. An IPDV measurement method based-on packet-pair sampling[J]. Journal of Computer Research and Development, 2004, 41(8): 1354-1360. (in Chinese)

[13] THOMPSON K, MILLER G J, WILDER R. Wide-area internet traffic patterns and characteristics[J]. IEEE Network, 1997, 11(6): 10–23.

[14] PAPAGIANNAKI K, MOON S, FRALEIGH C. Measurement and analysis of single-hop delay on an IP backbone network[J]. IEEE Journal on Selected Areas in Communications, 2003, 21(6): 908-921.

(Edited by LI Xiang-qun)

Foundation item: Projects(60473031, 60673155) supported by the National Natural Science Foundation of China; Project(2005AA121560) supported by the High-Tech Research and Development Program of China

Received date: 2006-06-28; Accepted date: 2006-09-27

Corresponding author: LI Wen-wei, PhD; Tel: +86-731-8821570-8424; E-mail: liww@hnu.cn