生长速率对定向凝固Zn-Al-Bi共晶合金显微组织、力学性能和电学性能的影响
来源期刊:中国有色金属学报(英文版)2016年第9期
论文作者:Yasin KARAMAZI ümit BAYRAM P?nar ATA Sezen AKS?Z Kaz?m KE?L?O?LU Necmettin MARA?LI
文章页码:2320 - 2335
关键词:定向凝固;锌铝合金;显微组织;显微硬度;拉伸强度;电学性能
Key words:directional solidification; zinc-aluminum alloy; microstructure; microhardness; tensile strength; electrical properties
摘 要:采用Bridgman型定向凝固炉在一定温度梯度和不同生长速率下制备Zn-5%Al-0.2%Bi(质量分数)合金。测量了定向凝固Zn-Al-Bi合金的枝晶间距、显微硬度、抗拉强度和电阻率。采用线性回归分析研究生长速率对合金枝晶间距、显微硬度、抗拉强度和电阻率的影响。在低生长速率下(小于450.0 μm/s),所得结果与在相似生长速率下定向凝固的Zn-Al合金的结果吻合,但与Jackson-Hunt共晶理论和高生长速率下的实验结果不同。Zn-Al-Bi共晶合金的临界生长速率为450 μm/s。从热流-温度曲线中可以得到,Zn-Al-Bi合金的熔化焓、固液相比热差以及熔化温度分别为112.55 J/g、0.291 J/(g?K)和660.20 K。
Abstract: Zn-5%Al-0.2%Bi (mass fraction) alloy was directionally solidified upward at a constant temperature gradient with a wide range of growth rates using a Bridgman-type directional solidification furnace. The eutectic spacings, microhardness, ultimate tensile strength and electrical resistivity for directionally solidified Zn-Al-Bi alloy were measured. Dependence of eutectic spacings, microhardness, ultimate tensile strength and electrical resistivity on growth rates was obtained by linear regression analysis. The results obtained in the present work for low growth rates (smaller than 450.0 μm/s) are in good agreement with experimental results obtained in previous work for directional solidified Zn-Al eutectic alloy with a similar growth rate but differs from the Jackson-Hunt eutectic theory and those obtained in previous experimental works at higher growth rates. The critical growth rate might be 450.0 μm/s for the Zn-Al-Bi eutectic alloy. From the plot of heat flow versus temperature, enthalpy of fusion, specific heat difference between liquid and solid phases and melting temperature for the Zn-Al-Bi alloy are found to be 112.55 J/g, 0.291 J/(g·K) and 660.20 K, respectively.
Trans. Nonferrous Met. Soc. China 26(2016) 2320-2335
Yasin KARAMAZI1,  BAYRAM2,
BAYRAM2,  ATA3, Sezen
ATA3, Sezen  4,
4, 
 2, Necmettin
2, Necmettin  5
5
1. Department of Physics, Institute of Science and Technology, Erciyes University, Kayseri 38039, Turkey;
2. Department of Physics, Faculty of Science, Erciyes University, Kayseri 38039, Turkey;
3. Department of Physics, Institute of Science and Technology,  50300, Turkey;
50300, Turkey;
4. Department of Physics, Faculty of Arts and Sciences,  50300, Turkey;
50300, Turkey;
5. Department of Metallurgical and Materials Engineering, Faculty of Chemistry and Metallurgical Engineering, 34220, Turkey
34220, Turkey
Received 16 October 2015; accepted 16 April 2016
Abstract: Zn-5%Al-0.2%Bi (mass fraction) alloy was directionally solidified upward at a constant temperature gradient with a wide range of growth rates using a Bridgman-type directional solidification furnace. The eutectic spacings, microhardness, ultimate tensile strength and electrical resistivity for directionally solidified Zn-Al-Bi alloy were measured. Dependence of eutectic spacings, microhardness, ultimate tensile strength and electrical resistivity on growth rates was obtained by linear regression analysis. The results obtained in the present work for low growth rates (smaller than 450.0 μm/s) are in good agreement with experimental results obtained in previous work for directional solidified Zn-Al eutectic alloy with a similar growth rate but differs from the Jackson-Hunt eutectic theory and those obtained in previous experimental works at higher growth rates. The critical growth rate might be 450.0 μm/s for the Zn-Al-Bi eutectic alloy. From the plot of heat flow versus temperature, enthalpy of fusion, specific heat difference between liquid and solid phases and melting temperature for the Zn-Al-Bi alloy are found to be 112.55 J/g, 0.291 J/(g·K) and 660.20 K, respectively.
Key words: directional solidification; zinc-aluminum alloy; microstructure; microhardness; tensile strength; electrical properties
1 Introduction
Zinc-based alloys have high strength and hardness, which means that they are the ideal alternative to machined, pressed, stamped and fabricated items. Complex net-shaped zinc housings with precise thin walls give excellent electrical performance and shielding properties for electronic connectors as well as shields, chassis and frames for handheld telecommunication and computing equipment. Zinc-based alloys have been used in many applications, including mobile phone antennae, portable computers, disk drives, radiofrequency circuits, transformer cores, high-quality filters, precision interlocking gears, and heat sinks, shutter mechanisms in cameras and many other consumer electrical and electronics consumer applications [1-3]. Zinc–aluminum (Zn–Al) alloys are gaining increasing attention due to their potential cost- and energy-effective, and environmentally friendly system for substituting several ferrous and non-ferrous alloys in various engineering applications [4-6]. They have several advantages over other commonly used casting alloys based on iron, aluminum and copper. For example, their machinability is better than cast iron; they are harder and stronger than aluminum and much cheaper than copper [7]. As for the Zn-Al alloy, previous works had been done mainly focused on directionally solidified near eutectic composition, dendritic growth [8-12] mechanical and corrosion properties [12-14].
Interstitial-free (IF) steel is a kind of very important structural material due to its eminent deep-pressing capability. It is widely used in making shells of automobiles and electrical appliances [15]. However, the erosion resistance of it is not satisfying. And coating IF steel products with protective materials have become the most popular and successful method to extend their service lifetime. For example, Zn and Zn-Al alloys, acting as both sacrificial anode and corrosion barrier, are effectively applied as protective coatings on them, especially in marine and high-temperature environment [16-20]. As a commercial coating method of Zn and Zn-alloys, hot-dipping has been developed by immersing the steel products into various melted Zn or Zn-alloy baths, for example, galvanized (Zn, <1% Al), galfan (5% Al-Zn), and galvalume (55% Al-Zn) [21-23].
Eutectic alloys are the basis of most casting alloys. Research initially focused on materials for high temperature structural applications, but it was soon broadened to non-structural materials for electric, magnetic, and optical applications [24]. Two important parameters of eutectic microstructure, which can be controlled experimentally, are the relative solidification parameters (temperature gradient and growth rate) and eutectic spacing. Solidification behavior and microstructural characteristics of eutectic alloys in many systems continue to attract interest because of their influence on the properties and performance of materials containing eutectic constituents.
Two-phase planar eutectic growth has been extensively studied since 1960’s for a wide range of binary alloy systems. Several authors made the extension to ternary systems, usually to investigate possible three- phase coupled growth configurations [25-30]. One of the essential challenges to materials science is to understand how multiphase microstructures form and how they can be controlled via deliberate selection of alloy composition and processing parameters. Multiphase solidification in multicomponent alloys is pertinent to many commercial materials and industrial processes, while also raising challenging questions from a fundamental point of view. Within the past few years, research activities have been dedicated to multiphase solidification of ternary and multicomponent alloys have experienced considerable amplification. Multiphase solidification of multicomponent materials attracts pronounced academic interest as well. The study of the solidification behavior of multicomponent and multiphase systems is an important question in understanding the different properties of these materials [25].
Solidification and melting are the transformations between the crystallographic and non-crystallographic states of a metal or alloys. These transformations are basic to such technological applications as ingot and continuous casting, and directionally solidification of composites and single crystals. An understanding of the mechanism of solidification and how it is affected by such parameters as temperature distribution, solidification conditions and alloying, are important in the control of the mechanical and electrical properties of cast metals and fusion welds [31].
As can be seen from literatures [8-14,26,32-53], the experiments on directional solidification were usually performed in a growth range of 2.0-500.0 μm/s at a constant low temperature gradient by using a Bridgman- type growth apparatus and the influence of growth rate on the microstructure parameters and microhardness were determined from experimental results. In the directional growth experiments, the experimental works with high growth rate (higher than the 500.0 μm/s) are more difficult.
The aims of present work were to perform directionally solidification experiments with high growth rates as well as low growth rates at a constant temperature and experimentally investigate the influences of high growth rates (v) as well as low growth rates on eutectic spacing (λ), microhardness (H), electrical resistivity (ρ) and ultimate tensile strength (σU) for directionally solidified ternary Zn-Al-Bi eutectic alloy.
2 Experimental
In the present work, the experimental procedure consists of alloy preparation, the microstructure observation and the measurements of solidification parameters, eutectic spacings, microhardness, ultimate tensile strength and electrical resistivity for directionally solidified ternary Zn-Al-Bi eutectic alloy. The phase diagram of Zn-Al-Bi ternary alloy was determined by  et al [54]. According to the phase diagram of Zn-Al-Bi ternary alloy, the composition of Zn-Al-Bi was chosen as Zn-5%Al-0.2%Bi (mass fraction) to grow eutectic η-Zn (Zn solution) and (Al)'(η-Zn+a(Al)) phases. In present work, the melting point of Zn-5%Al- 0.2%Bi alloy was also detected to be 660.20 K.
et al [54]. According to the phase diagram of Zn-Al-Bi ternary alloy, the composition of Zn-Al-Bi was chosen as Zn-5%Al-0.2%Bi (mass fraction) to grow eutectic η-Zn (Zn solution) and (Al)'(η-Zn+a(Al)) phases. In present work, the melting point of Zn-5%Al- 0.2%Bi alloy was also detected to be 660.20 K.
2.1 Measurement of temperature gradient G and growth rates v
The temperature of the Bridgman-type furnace was controlled by a Pt/Pt-13%Rh thermocouple placed between the heating element and the alumina tube as shown Fig. 1. The temperature could be controlled to about ±0.1 K during the run. Throughout the experiment, the thermocouples were placed into the capillary alumina tubes (0.8 mm ID, 1.2 mm OD) which were positioned approx. 20 mm apart and parallel to the heat flow direction inside the crucible. Temperature distribution was obtained by measuring the temperature in the sample during the heating and cooling by five chromel/alumel thermocouples (type-K) which were placed in the sample [47]. Accuracy of the thermocouples was checked by slowly solidifying the Zn-Al-Bi samples (where thermocouples were placed parallel to the heat flow and perpendicular to the heat flow direction). The measured Te difference was less than 0.5 K with differently placed thermocouples. All the thermocouple leads were taken to an ice/water cold junction, then to a WPA analog potentiometer and to a Kipp–Zonen chart recorder capable of recording to 1 μV. Temperatures of all the thermocouples were recorded during the run. Temperatures of the second thermocouple at the solid–liquid interface and then third thermocouple in the liquid were recorded simultaneously for measurement of the temperature gradients at the solid/liquid interface in the liquid. The positions of the thermocouples were measured after the quenching. Cooling water level (with the constant temperature) was always kept at the same position in order to check the furnace temperature. Thus, the sample temperature was constant. The temperature gradient can be changed by changing the sample temperature and/or the distance between the cooling water level and the hot stage. G can be kept constant during the run because the temperature of the cooler and the hotter part of the furnace and the distance between them were constant. It was found that the pulling speed was similar to the growth rates; this may be due to the metal sample holder and the graphite crucible which have good thermal conductivity. The growth rate was calculated with two different methods. In the first method, the values for the growth rate were calculated from the measurements of the time taken for the solid/liquid interface to pass the thermocouples separated by a known distance. In the second method, solidification time and solidification distance (on the longitudinal section of the polished sample) were measured. The ratio of the distance to the time was measured to obtain the growth rates and these were similar for both methods.
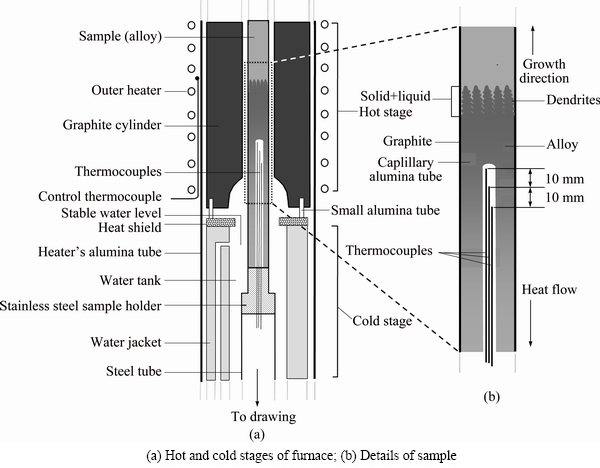
Fig. 1 Details of Bridgman-type directional solidification furnace
2.2 Sample production and microstructure observation
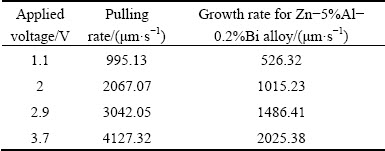
The composition of Zn-Al-Bi ternary alloy was chosen to be Zn-5%Al-0.2%Bi to grow the eutectic phases from ternary liquid. Thus, the Zn-Al-Bi molten alloy was prepared under the vacuum by using 99.99% pure zinc, 99.99% pure aluminum and 99.999 % pure bismuth and poured into graphite crucibles (200 mm in length, 4 mm in inner diameter and 6.35 mm in outer diameter), held in a specially constructed casting furnace (hot filling furnace) at approximately 50 °C above the melting point of eutectic alloy. The molten alloy was directionally solidified from bottom to top to ensure that the crucible was completely full. Then, each sample was positioned in a Bridgman-type furnace within a graphite cylinder (300 mm in length, 10 mm in inner diameter and 40 mm in outer diameter). Solidification of the samples was carried out with different growth rates (v=8.82- 2025.38 μm/s) at a constant temperature gradient (G=3.42 K/mm) by using different speeded synchronous motors. In practice, there are six kinds of commercial synchronous motors (1, 2, 5, 10, 20, 60 r/s). The maximum growth rate of 500.0 μm/s can be obtained with 60 r/s synchronous motor at a constant temperature gradient. In present work, a driving system was constructed by using a hand drill’s motor to get high growth rates (from 212.45 to 2025.38 μm/s) at constant temperature gradient. Applied voltages versus pulling rates or pulling rates versus growth rates obtained with the constructed driving system are given in Table 1. The details of Bridgman-type directional solidification furnace and experimental procedures are also given in Refs. [42,55,56].
Table 1 Voltages versus pulling rates or pulling rates versus growth rates obtained with constructed driving system
The quenched sample was removed from the graphite crucible and cut into lengths typically 15 mm. The longitudinal and transverse sections were ground flat with SiC paper (120, 320, 500, 1000, 2000 grit), and then, ground samples were cold mounted with epoxy-resin. After polishing, the samples were etched with a 10% hydrofluoric acid in water enchant for 30-45 s. After metallographic process, the microstructures of the samples were revealed.
The microstructures of samples were photographed from both transverse and longitudinal sections with an Olympus DP12 digital camera placed in conjunction with an Olympus BHX type light optical microscope and a LEO scanning electron microscopy (SEM). But the resolution of optical microscopy was poor to see microstructure of directionally solidified samples with high growth rates, thus, the microstructures of samples were photographed from longitudinal and transverse sections with a LEO scanning electron microscopy. Typical SEM images from longitudinal and transverse sections of directionally solidified Zn-Al-Bi eutectic samples with high growth rates at a constant temperature gradient are shown in Fig. 2.
2.3 Measurements of solidification parameters and eutectic spacing
The temperature in the specimen was measured by using three K-type 0.25 mm diameter insulated thermocouples fixed within the sample with spacing of 10-20 mm. The cooling rates were recorded by using the data-logger via the computer during growth. The temperature gradient (G=DT/DX) in the liquid phase and the value of growth rate (V=DX/Dt) for each sample was determined by using the measured values of DT, DX and Dt. Details of the measurements of DT, DX and Dt are given in Refs. [42,55,56].
The measurements of λ were made from the photographs of microstructures with a linear intersection method [37]. The λ values measured on the transverse section are more reliable than the λ values measured on the longitudinal section of the sample [38,39]. As can be seen from Fig. 2, the structure of Zn-5%Al-0.2%Bi samples becomes fine lamellar with increasing the growth rates.
2.4 Measurement of microhardness
The mechanical properties of any solidified materials are usually determined with hardness test, tensile stress test, compressive stress test, ductility test, etc. Since true tensile stress testing of solidified alloys gave inconsistent results with a wide scatter due to the strong dependence on the solidified sample surface quality, the mechanical properties were monitored by hardness testing, which is one of the easiest and most straightforward techniques.
One of the purposes of present work was to reveal the relationship between the solidification processing parameters and microhardness for directionally solidified Zn-Al-Bi eutectic alloy. The Vickers hardness (H) is the ratio of a load applied to the indenter to the surface area of the indentation. This is given by
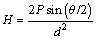 (1)
(1)
where H is the Vickers microhardness in N/mm2, P is the applied load (N), d is the mean diagonal of the indentation (mm), θ is the angle between opposite faces of the diagonal indenter (136°). Microhardness measurements in the present work were made with a Future-Tech FM-700 model hardness measuring test device using a 10 g to 50 g load and dwell time of 10 s, giving a typical indentation depth of about 40 to 60 μm, which is significantly smaller than the original solidified samples. Microhardness is the average of at least 30 measurements on the transverse sections (HT).
2.5 Measurement of tensile strength
The behavior of material is mainly determined by various mechanical properties of the material when subjected to different loading conditions. Such properties mainly include elastic modulus, various types of strength of the material, hardness, ductility etc. and are found to be very important both for design and manufacturing viewpoint. Three basic types of stresses which are produced when a material is subjected to various loading conditions are tensile stress, compressive stress and shear stress.

Fig. 2 Typical SEM images from longitudinal and transverse sections of directional solidified Zn-5%Al-0.2%Bi eutectic alloy at constant temperature gradient (G=3.42 K/mm) with low growth rates and high growth rates
Tensile strength is defined as the ability of a material to support axial load without rupture and is determined through the tensile test. When equal and opposite forces are applied simultaneously at both the ends that pulls the material, it tries to elongate it and the diameter reduces.
Generally, in design application, the stress-strain curve is used as there is no expectation of change in shape due to strain. Stress-strain curve is mainly illustrated by taking original cross section and original length.
One of the aims of present work is to measure the tensile stress. The tests of tensile was performed at room temperature at a strain rate of 10-3 s-1 with a Shimadzu AG-IS universal testing machine. The data collected from the tensile test can be analyzed using the following formula to determine the stress (σ):
 (2)
(2)
where σ is the stress in N/mm2 (or MPa), F is the applied force (N), A is the original cross sectional area of the sample.
Strain (ε) at any point is the ratio between changes in length to the original gage length.
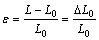 (3)
(3)
where ε is the strain ( mm/mm), L is the length at any point during elongation (mm) and L0 is the original gage length (mm).
The round rod tensile samples with the diameter of 4 mm and gauge length of 50 mm were prepared from directionally solidified rod samples with different solidification parameters. The tensile axis was chosen parallel to the growth direction of the sample and the tests were repeated three times.
2.6 Measurement of electrical resistivity
The electrical resistivity (ρ) is the main fundamental properties of materials such as density, melting point, entropy, enthalpy, resistance, and crystal structure parameters. Although the value of ρ for pure metallic materials was obtained theoretically and experimentally, there are not enough information and data available about electrical resistivity (ρ) of metallic alloys. The value of ρ for alloys changes, as in pure materials, not only with temperature, grain size, and grain boundary numbers but also with compositions of alloy [57]. The four-point probe method is the most widely used technique for electrical profile measurement of materials. The method has proven to be a convenient tool for the resistivity measurement.
In present work, the electrical resistivity (ρ) of Zn-5%Al-0.2%Bi eutectic alloy, directional solidified with different high growth rates (8.82-2025.38 μm/s) at constant temperature gradient (3.42 K/mm) were measured by the DC four-point probe method at room temperature to see the dependency of electrical resistivity at the high growth rates.
2.7 Determination of specific heat and enthalpy
The specific heat difference between liquid and solid phases (△cp) and the enthalpy of fusion (ΔH) of Zn-Al-Bi eutectic alloy (5-10 mg) were determined because they are very important parameters for technological applications. DSC thermal analysis (Perkin Elmer Diamond model) was performed in the temperature range from room temperature to 800 K at a heating rate of 10 K/min under a constant stream of nitrogen at atmospheric pressure.
We used a reference material (a sapphire disk) in determining specific heat. These reference data are used to ‘‘correct’’ sample data at every temperature. The size of the signal which is used to calculate the specific heat is proportional to the heating rate, so it follows that faster heating rates will produce larger signals, which would give more accurate data. However, if the heating rate is too high, the temperature gradients in the sample will be large and this may introduce other errors in the measurement. It is normal to use heating rates between 5 and 20 K/min. The heating rate in this study was 10 K/min, which is mostly recommended. The difference between the sample curve and the baseline curve is measured in milliwatts and converted to specific heat difference between liquid and solid phases (△cp). The DSC curve was obtained for the Zn-Al-Bi eutectic alloy; then, ΔH was calculated as the area under the peak by numerical integration.
3 Results and discussion
3.1 Dependence of eutectic spacings on growth rate
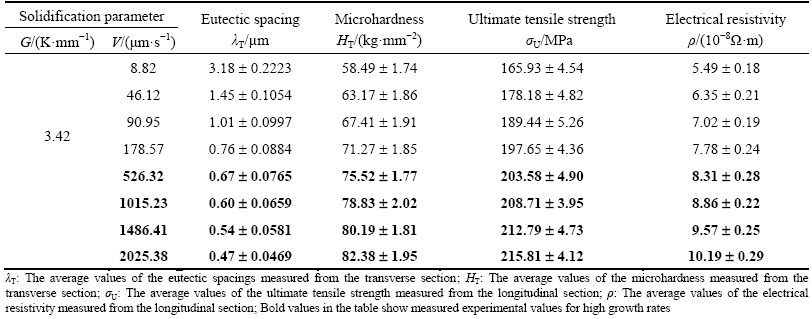
In order to clearly see the effect of low and high growth rates (v) on eutectic spacings (λ) microhardness (HT), ultimate tensile strength (σU) and electrical resistivity (ρ) at room temperature in Zn-Al-Bi eutectic system, the samples were unidirectionally solidified with a wide range of growth rates (8.822025.38 m/s) at constant temperature gradient (3.42 K/mm) by using a Bridgman-type growth apparatus.
The solid solubilities of Bi in solid Zn and Al are 0.2% Bi and 0.1% Bi at 527 and 930 K, respectively [58]. According the phase diagram of Zn-Al-Bi ternary alloy and solid solubility of Bi in solid Zn and Al, the composition of Zn-Al-Bi was chosen as Zn-5%Al- 0.2%Bi to growth eutectic η-Zn (Zn solution) and (Al)' (η-Zn+a(Al)) phases. The quantitative chemical composition analyses of η-Zn matrix and η-Zn+a(Al) were carried out by using an energy dispersive X-ray analyzer (EDX) and the results are given in Fig. 3. According to EDX results as shown in Fig. 3 and the solubility of components in each phase, grey and black phases were identified as Zn solution (η-Zn) matrix phase and (Al)' (η-Zn+a(Al)) Zn-rich phase, respectively.
For eutectic and near-eutectic composition alloys, the fluid-flow effect is negligible [40]. Although fluid- flow does not exist in thin samples (<1 mm inner diameter), its effect is small in the bulk samples. Because the density of the liquid also depends on the solute concentration, the rejection of solute modifies the density field within solute layer. If the solute layer is heavier than the solvent (as in Zn-Al) then both the solutal and thermal buoyancy forces are parallel to the gravity vector. Under this ideal case of no horizontal variation of temperature, this arrangement is hydrostatically stable (i.e., fluid motion is negligible), and the transport of solute must be solely due to molecular diffusion along the growth direction [40]. The inner diameter of crucible used in present work is 4 mm. So, the fluid-flow effect on lamellar eutectic is negligible.
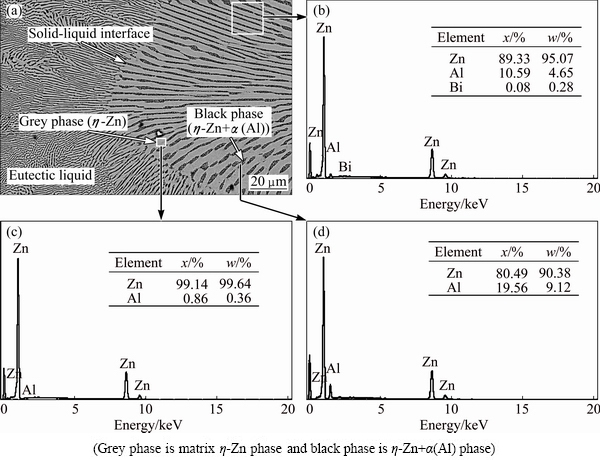
Fig. 3 Chemical composition analysis of Zn-5.0%Al-0.2%Bi eutectic alloy by using SEM-EDX
As expected, the formations of the microstructures have varied with the growth rates and as the growth rate is increased, the eutectic spacings decrease at a constant temperature gradient. The highest eutectic spacings were obtained with the minimum growth rate (8.82 μm/s) as shown in Figs. 2 (a) and (b) while the smallest eutectic spacing was obtained with the maximum growth rate (2025.38 μm/s) as shown in Figs. 2(g) and (h).
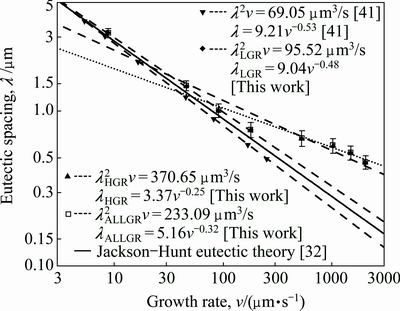
Fig. 4 Variation of eutectic spacing with growth rates and comparison of experimental present results with previous similar experimental result [41] and predicted value from Jackson-Hunt eutectic theory for Zn-5.0%Al alloy [32]
The measured values of eutectic spacings in the Zn-Al-Bi alloy as a function growth rates at a constant temperature gradient are given in Fig. 4. A comparison of present results with the previous experimental results for binary Zn-Al eutectic alloy [41] is also given in Fig. 4. The variation of λ versus v is essentially linear on the logarithmic scale. As can be seen from Fig. 4, the data form straight lines, the linear regression analysis gives the proportionality equation as
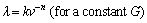 (4)
(4)
where k is a constant and n is an exponent value of growth rate. The relationships between the eutectic spacing and growth rates were determined for directionally solidified Zn-5%Al-0.2%Bi alloy with low growth rates (8.82-178.57 μm/s), high growth rates (526.32-2025.38 μm/s) and all growth rates (8.82- 2025.38 μm/s), respectively at a constant temperature gradient (3.42 K/mm) as
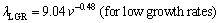 (5a)
(5a)
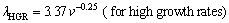 (5b)
(5b)
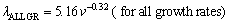 (5c)
(5c)
A comparison of present result with the Jackson- Hunt eutectic theory [32] and previous experimental work [41] for Zn-Al eutectic alloy is also shown in Fig. 4. ENGIN et al [41] have done similar experimental work with a range of growth rates (5.32-250.0 μm/s) at a constant temperature gradient (8.50 K/mm) by using a Bridgman-type growth apparatus for Zn-Al eutectic alloy. It can be seen from Fig. 4 that the line of λLGR versus v for low growth rates determined in present work is slightly higher than the lines of λ versus v determined by ENGIN et al [41] and predicted from Jackson-Hunt eutectic theory [32]. This small disparity might be due to the addition of Bi. But the line of λHGR versus v for high growth rates determined in present work for high growth rates is fairly above the lines of λ versus v determined by ENGIN et al [41] and predicted from Jackson-Hunt eutectic theory [32]. This large disparity is definite due to high growth rates rather than the alloying element of Bi.
The exponent value of 0.48 relating to growth rate for low growth rates obtained in present work is very close to the exponent values of 0.53 and 0.5 relating to growth rate determined by ENGIN et al [41] and predicted from Jackson-Hunt eutectic theory [32], respectively. But the exponent value of 0.25 relating to growth rate for high growth rates obtained in present work is about two times smaller than the exponent values of 0.53 and 0.5 relating to growth rate determined by ENGIN et al [41] and predicted from Jackson-Hunt eutectic theory [32], respectively. Even if all measurements of eutectic spacings for all growth rates are considered together, the exponent value of 0.32 relating to growth rate obtained in present work is close to half of the exponent values of 0.53 and 0.5 relating to growth rate determined by ENGIN et al [41] and predicted from Jackson-Hunt eutectic theory [32], respectively.
From experimental results, it can be concluded that the Jackson-Hunt eutectic theory [32] differs from present experimental results at higher growth rates (larger than 250.0 μm/s). The Jackson-Hunt eutectic theory [32] is based on steady state growth. According to experimental results, the limit of steady state growth rate is about 450 μm/s for Zn-Al-Bi eutectic alloy. When the growth rate is above 450 μm/s, the growth may be transient (unsteady state). Thus, the experimental result for Zn-Al-Bi eutectic alloy differs from the Jackson- Hunt eutectic theory [32] at high growth rates (higher than 450.0 μm/s).
In present work, the bulk growth rates for low, high and all growth rates were also determined to be 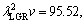
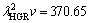 and
and 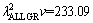 μm3/s, respectively for Zn-5%Al-0.2%Bi alloy. When the value of
μm3/s, respectively for Zn-5%Al-0.2%Bi alloy. When the value of 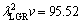 μm3/s obtained in present work is in a good agreement with the values of 69.05 and 72.39 μm3/s obtained by ENGIN et al [41] for Zn-5.0%Al solidified with low growth rates and predicted from the Jackson-Hunt model [32], respectively, the values of
μm3/s obtained in present work is in a good agreement with the values of 69.05 and 72.39 μm3/s obtained by ENGIN et al [41] for Zn-5.0%Al solidified with low growth rates and predicted from the Jackson-Hunt model [32], respectively, the values of 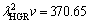 and
and  μm3/s obtained in present work are about five and three times larger than the values of 69.05 and 72.39 μm3/s obtained by ENGIN et al [41] for Zn-5.0%Al solidified with low growth rates and predicted from the Jackson-Hunt model [32], respectively.
μm3/s obtained in present work are about five and three times larger than the values of 69.05 and 72.39 μm3/s obtained by ENGIN et al [41] for Zn-5.0%Al solidified with low growth rates and predicted from the Jackson-Hunt model [32], respectively.
3.2 Dependence of microhardness on growth rate and eutectic spacing
It is well known that some important solidification parameters, such as growth rate, significantly affect the microstructural scale as well as the mechanical properties of metals. Materials processed via directional solidification tend to show advantages of refined micro- structure, reduced microsegregation etc [59,60]. Because the mechanical properties of a material depend largely on its microstructure, controlled formation of such microstructures is essential to develop new materials with desired properties [61-64].
From HALL [65] and PETCH [66] papers, the grain size dependence of yield strength can be described by the equation:
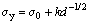 (6)
(6)
where k is a constant which is the hardness against deformation and d is the mean grain size or characteristic length scale, that the grain size dependence is related to the length of a slip band, and that the maximum slip band length is determined by the grain size. In the present work, the lamellar distance (λ) is related with the mean grain size and λ is the proportional inverse the square root of growth rate (v) according to the eutectic growth theory. Thus, the Hall-Petch type relationships between the microhardness and the microstructure spacing or growth rate can be expressed as follows:
 (7)
(7)
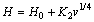 (8)
(8)
where H0 is the initial microhardness of equilibrated solid phase with liquid at the melting temperature and K1 and K2 are constants which depend on kind of materials. The values of H0, K1 and K2 can be experimentally determined.
One of the purposes of present work is to obtain the dependence of HT on v and λ for directionally solidified zinc-based alloy (Zn-5%Al-0.2%Bi) with attractive physical and mechanical properties [67-69]. The variations of microhardness (HT) as a function of eutectic spacing and high growth rates (v) at a constant temperature gradient (G=3.42 K/mm) were plotted in Figs. 5 and 6. ENGIN et al [41] have done similar experimental work with a range of growth rates (5.32-250.0 μm/s) at a constant temperature gradient (8.50 K/mm) by using a Bridgman-type growth apparatus for same alloy. As can be seen from Fig. 5, Fig. 6 and Table 2, the value of HT increases with the increasing value of v and the decreasing values of λ at a constant temperature gradient, G. The relationships between the microhardness and eutectic spacing and growth rates were obtained by using linear regression analyze. From Fig. 5 and Fig. 6, the dependences of HT on eutectic spacing, and low, high and all growth rates for directionally solidified Zn-5%Al-0.2%Bi alloy have been expressed with linear regression analyze.
In present work, the dependences of HT on eutectic spacings and low, high and all growth rates were obtained as follows:
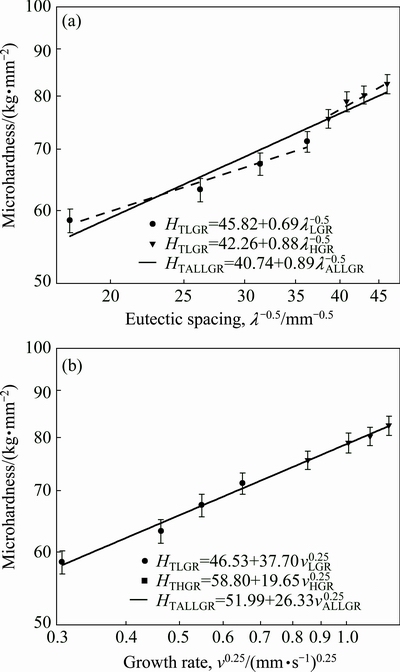
Fig. 5 Variations of Hall-Petch type equations of microhardness (HT) as a function of eutectic spacings (λ) (a) and growth rates (v) (b) for directionally solidified Zn-Al-Bi eutectic alloy with different growth rates (8.82-2025.38 μm/s) at a constant temperature gradient (G=3.42 K/mm)
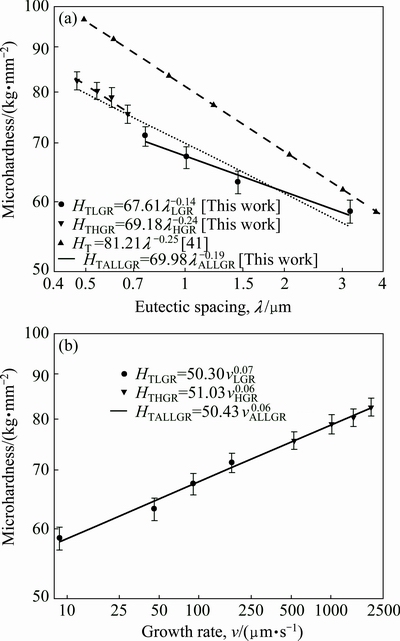
Fig. 6 Variations of microhardness (HT) as a function of eutectic spacings (λ) (a) and growth rates (v) (b) for directionally solidified Zn-5.0%Al alloy [41] and Zn-Al-Bi eutectic alloy with different growth rates (8.82-2025.38 μm/s) at a constant temperature gradient (G=3.42 K/mm)
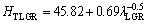 (9a)
(9a)
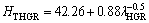 (9b)
(9b)
 (9c)
(9c)
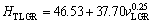 (10a)
(10a)
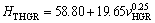 (10b)
(10b)
 (10c)
(10c)
and the dependences of HT on eutectic spacings and low growth rates were obtained by ENGIN et al [41] for directionally solidified Zn-5.0%Al alloy as
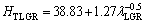 (11a)
(11a)
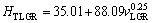 (11b)
(11b)
As can be seen from Eqs. (9)-(11), the coefficient values of λLGR and vLGR (0.69 and 37.70) for Zn-5%Al- 0.2%Bi alloy obtained in present work are about half of the coefficient values of λLGR and vLGR (1.27 and 88.09) for Zn-5.0%Al alloy obtained in previous work [41] but the initial values of H0 (45.82 and 46.53) for Zn-Al-Bi alloy obtained in present work are 25% larger than the initial values of H0 (38.83 and 35.01) for Zn-5.0%Al alloy obtained in previous work [41]. This variety is due to solid solution of Bi in matrix phase of solid Zn.
Table 2 Solidification processing parameters, eutectic spacings, microhardness, ultimate tensile strength and electrical resistivity for directional solidified Zn-5.0% Al-0.2%Bi eutectic alloy
As can be seen from Figs. 5(a) and (b) and Eqs. (9) and (10), dependence of microhardness on eutectic spacing is stronger at high growth rates rather than low growth rates when dependence of microhardness on growth rate is stronger at low growth rates rather than high growth rates for directionally solidified Zn-5%Al-0.2%Bi alloy.
It can be also seen from Figs. 6(a) and (b) that an increase in solidification parameters leads to an increase in the HT values and an increase in eutectic spacings leads to a decrease in the HT values. The dependences of HT on growth rate and eutectic spacing was also determined as an order of growth rate and eutectic spacing by linear regression analysis and the relationship between them can be also expressed as
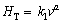 (12)
(12)
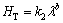 (13)
(13)
where k1 and k2 are constants and a and b are the exponent values relating to the growth rate and eutectic spacing. Figures 6(a) and (b) show the variation of HT as a function of v at a constant G and the variation of HT as a function of λ at a constant G, respectively and a comparison with the previous experimental result for binary eutectic alloy [41].
The relationships between HT and v for low, high and all growth rates were determined as
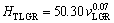 (14a)
(14a)
 (14b)
(14b)
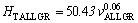 (14c)
(14c)
The relationships between HT and λ for low, high and all growth rates were determined as
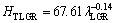 (15a)
(15a)
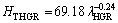 (15b)
(15b)
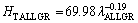 (15c)
(15c)
The exponent value relating to growth rate (0.06) for directional solidified Zn-5%Al-0.2%Bi alloy with all growth rates is in good agreement with the exponent values of 0.06 and 0.10 obtained in Refs. [52,70-72]. Also, the exponent value relating to eutectic spacing, λ (0.19) is also in good agreement with the exponent values of λ (0.20-0.28) obtained by different researchers [52,70-72] for different eutectic alloys.
3.3 Dependence of tensile strength on growth rate and eutectic spacing
Typical stress-strain curves for directionally solidified Zn-5%Al-0.2%Bi alloy with different growth rates were plotted and are shown in Fig. 7. According to stress-strain curves, the value of maximum tensile stress increases as growth rate increases.
As can be seen from Fig. 8 and Table 2, the value of σU increases with the increasing value of v and the decreasing values of λ at a constant temperature gradient, G. The relationships between the ultimate tensile strength and eutectic spacing and growth rates were obtained by using linear regression analyze. From Fig. 8, the dependences of σU on eutectic spacing and low or high growth rates for directionally solidified Zn-5%Al-0.2%Bi alloy have been expressed with linear regression analysis.
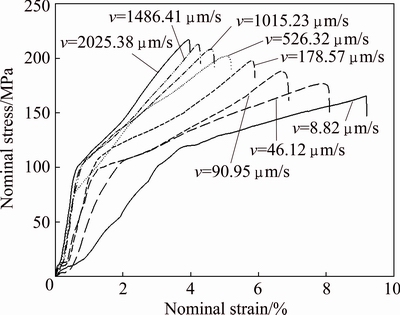
Fig. 7 Typical nominal stress-strain curves for directionally solidified Zn-Al-Bi eutectic alloy with different growth rates (8.82-2025.38 μm/s) at constant temperature gradient (G=3.42 K/mm)
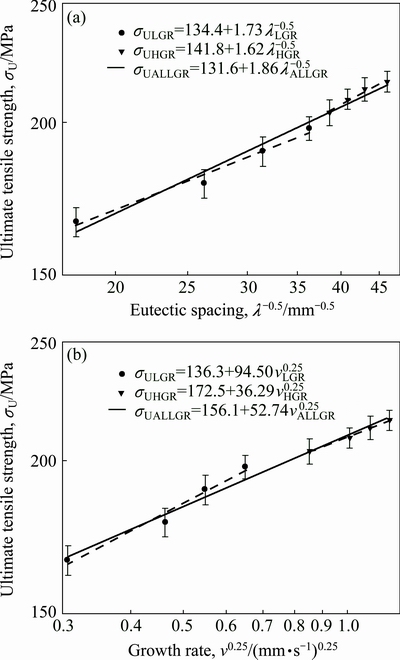
Fig. 8 Variations of Hall-Petch type equations of ultimate tensile strength as function of eutectic spacings (λ) (a) and growth rates (v) (b), for directionally solidified Zn-Al-Bi eutectic alloy with different growth rates (8.82-2025.38 μm/s) at constant temperature gradient (G=3.42 K/mm)
In present work, the dependences of σU on eutectic spacings and low, high and all growth rates were obtained as follows:
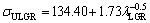 (16a)
(16a)
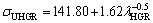 (16b)
(16b)
 (16c)
(16c)
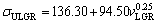 (17a)
(17a)
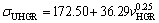 (17b)
(17b)
 (17c)
(17c)
Variation of ultimate tensile strength with growth rate and eutectic spacing for Zn-Al-Bi eutectic alloy is plotted in Fig. 9. A comparison of present results with the experimental result obtained in previous work for Zn-1.26%Al alloy [73] is also given in Fig. 9. It can be seen from Fig. 9 and Table 2 that the value of tensile strength for Zn-Al-Bi eutectic alloy increases from 165.93 to 215.81 MPa with increasing growth rate from 8.82 to 2025.38 μm/s and the relationships between σU and v for low, high and all growth rates were determined as
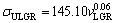 (18a)
(18a)
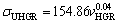 (18b)
(18b)
 (18c)
(18c)
The relationships between σU and λ for low, high and all growth rates were determined as
 (19a)
(19a)
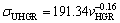 (19b)
(19b)
 (19c)
(19c)
The exponent value of 0.05 for Zn-Al-Bi eutectic alloy is five times smaller than that of 0.24 obtained for Zn-1.26%Al alloy [73] but the coefficient value of 150.50 for Zn-Al-Bi eutectic alloy is slightly larger than that of 144.00 obtained for Zn-1.26%Al alloy [73]. This disagreement might be due to high growth rates and compositional dissimilarities obtained by adding alloying element of Bi. It appears that the size of the η-Zn and a(Al) phases governs the properties, and the alignment of colonies due to unidirectional solidification is masked by the particle size effect.
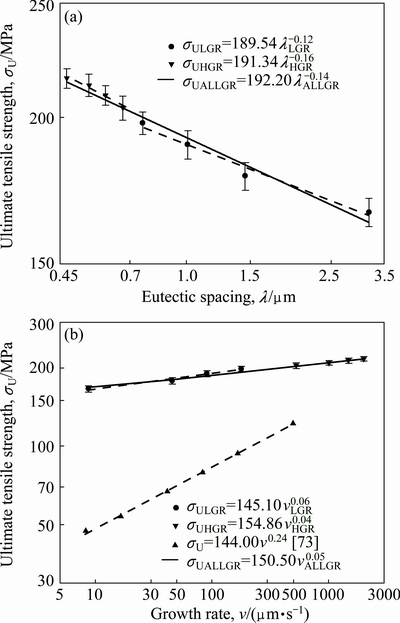
Fig. 9 Variations of ultimate tensile strength as function of eutectic spacing (a) and growth rates (b) for directionally solidified Zn-Al [73] and Zn-Al-Bi eutectic alloy with different growth rates (8.82-2025.38 μm/s) at constant temperature gradient (G=3.42 K/mm)
3.4 Dependence of electrical resistivity on growth rate and eutectic spacing
The electrical property, i.e., resistivity (ρ) of directional solidified materials also depends on solidification parameters, i.e., the growth rates (v). The relationships among the resistivity (ρ) and lamellar spacings (λ) can be expressed by the Hall-Petch type relationships as follows:
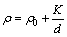 (20)
(20)
where K is a constant which is the initial resistivity and d is the mean grain size or characteristic length scale. In present work, the mean grain size can be the lamellar distance (λ) and λ is also the proportional inverse the square root of growth rate (v) according to eutectic growth theory.
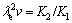 (21)
(21)
Thus, the Hall-Petch type relationships between electrical resistivity and the microstructure spacing or growth rate can be expressed as follows:
ρ=ρ0+K3λ-1 (22)
ρ=ρ0+K4v1/2 (23)
where ρ0 is the initial resistivity of equilibrated solid phase with liquid at the melting temperature and K5 and K6 are constants which depend on the kind of materials. The values of ρ0, K3 and K4 can be experimentally determined.
The variations of electrical resistivity (ρ) of Zn-Al-Bi eutectic alloy (3.42 K/mm) with growth rates were plotted. From graph of the electrical resistivity (ρ) of Zn-Al-Bi eutectic alloy versus growth rates, the relationship between the electrical resistivity and high growth rates and low growth rates for Zn-Al-Bi alloy was obtained by using linear regression analysis in present work.
As mentioned above, the electrical resistivities of directionally solidified samples for directionally solidified Zn-5%Al-0.2%Bi alloy were measured with the four-point probe method at room temperature. The variations of electrical resistivity (ρ) with the growth rate (v) and eutectic spacing (λ) are plotted in Fig. 10. It can be seen from Fig. 10 and Table 2 that the increase in the v and decrease in the λ lead to a increase in ρ values. Linear regression analysis yields a relationship between resistivity and eutectic spacing for directionally solidified Zn-Al-Bi alloy at G=3.42 K/mm as
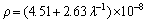 (24)
(24)
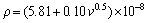 (25)
(25)
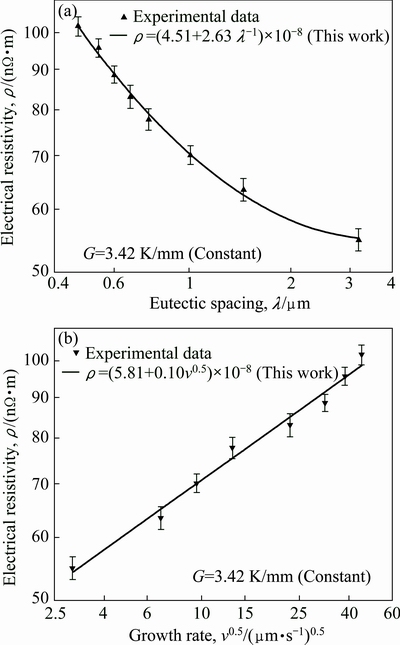
Fig. 10 Variations of Hall-Petch type equations electrical resistivity as function of eutectic spacing (a) and growth rate (b) for directionally solidified Zn-Al-Bi eutectic alloy with different growth rates (8.82-2025.38 μm/s) at constant temperature gradient (G=3.42 K/mm)
Electrical resistivities of pure Al, pure Zn and pure Bi are about 2.65×10-8, 5.9×10-8 and 129×10-8 Ω·m at room temperature, respectively. Also, a comparison of present results with the experimental result obtained in previous work for Zn-1.26%Al alloy [73] is given in Fig. 11. It can be seen from Fig. 11 and Table 2 that the value of electrical resistivity for Zn-Al-Bi eutectic alloy increases from 5.49×10-8 to 10.19×10-8 Ω·m with increasing growth rate from 8.82 to 2025.38 μm/s and the relationship between ρ and v was found to be as
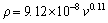 (26)
(26)
The dependence of ρ on v was obtained by  and
and  [73] for directionally solidified Zn-1.26%Al alloy as
[73] for directionally solidified Zn-1.26%Al alloy as
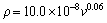 (27)
(27)
As can be seen from Eqs. (26) and (27), the exponent value of 0.11 for Zn-Al-Bi eutectic alloy is the twice that of 0.06 obtained for Zn-1.26%Al alloy [73] but the order of coefficient value obtained for directional solidified Zn-Al-Bi eutectic alloy is in good agreement with that obtained in Ref. [73]. A comparison of the electrical resistivity depends on growth rates for Zn-Al-Bi eutectic alloy with the electrical resistivity dependence on growth rates for Zn-1.26%Al alloy is also shown in Fig. 11. As can be seen from the slope of the line of variation of electrical resistivity with temperature for Zn-Al-Bi eutectic alloy is bigger than that with temperature for Zn-1.26%Al eutectic alloy. As mentioned above, although electrical resistivity of Bi is higher than electrical resistivities of Zn and Al, this large disparity is definitely due to high growth rates and adding alloying element of Bi.
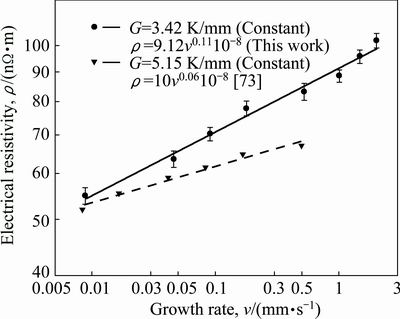
Fig. 11 Variations of electrical resistivity (ρ) as function of growth rates (v) for directionally solidified Zn-Al-Bi and Zn-Al [73] alloys with different growth rates at constant temperature gradient
3.5 Determination of thermal properties of Zn-Al-Bi eutectic alloy
Zn-Al-Bi eutectic alloy was heated with a heating rate of 10 K/min from room temperature to 800 K by using a Perkin Elmer Diamond model DSC and the heat flow versus temperature for Zn-Al-Bi eutectic alloy is given in Fig. 12. It can be seen from Fig. 12, the melting temperature of Zn-Al-Bi eutectic alloy was detected to be 660.20 K. The value of enthalpy of fusion (ΔH) and specific heat difference between liquid and solid phases (△cp) for Zn-Al-Bi eutectic alloy were determined to be 112.55 J/g, and 0.291 J/(g·K), respectively, by numerical integration from area under the peak. The values of △H and △cp in this work are in good agreement with the values 113.37 J/g, 0.309 J/(g·K) and 113.4 J/g, 0.294 J/(g·K) obtained by SEVDA et al [41] for Zn-5Al and  and
and  [73] for Zn-1.26Al alloy, respectively. The recommended values of enthalpy of fusion (△H) and the specific heat difference between liquid and solid phases (△cp) are 396.96 J/g and 0.896 J/(g·K) for pure aluminum and 111.91 J/g and 0.389 J/(g·K) for pure zinc [74], respectively.
[73] for Zn-1.26Al alloy, respectively. The recommended values of enthalpy of fusion (△H) and the specific heat difference between liquid and solid phases (△cp) are 396.96 J/g and 0.896 J/(g·K) for pure aluminum and 111.91 J/g and 0.389 J/(g·K) for pure zinc [74], respectively.
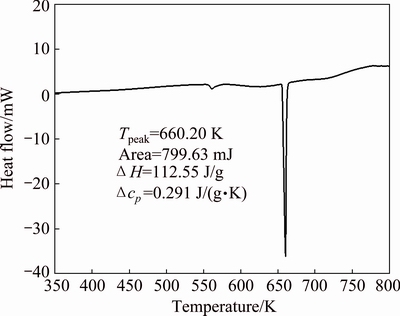
Fig. 12 Heat flow curve versus temperature for Zn-Al-Bi eutectic alloy at a heating rate of 10 K/min
4 Conclusions
1) The values of eutectic spacing decrease as the values of v increase. The exponent value of v (0.32) for Zn-5%Al-0.2%Bi alloy solidified with high growth rates is different from the exponent values predicted with the Jackson-Hunt eutectic theory [32] and obtained in previous experimental works. From experimental result, it can be concluded that the Jackson-Hunt eutectic theory [32] differs from present experimental results at higher growth rates. This critical growth rate might be 450.0 μm/s for the Zn-Al-Bi eutectic alloy.
2) Dependence of microhardness on growth rates and eutectic spacings were obtained for low, high and all growth rates at a constant G=3.42 K/mm. The results obtained in present work for low growth rates are in a good agreement with experimental results obtained in previous work for directional solidified Zn-Al eutectic alloy with a similar growth range [41].
3) Dependences of ultimate tensile strength on growth rates and eutectic spacings were obtained to be 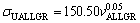 and
and 
 by using linear regression analysis for all growth rates.
by using linear regression analysis for all growth rates.
4) Dependence of electrical resistivity of directionally solidified Zn-Al-Bi alloy on growth rates and eutectic spacing was obtained to be 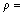
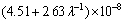 and
and 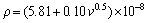 at room temperature.
at room temperature.
5) From the plot of heat flow versus temperature, enthalpy of fusion, specific heat difference between liquid and solid phases and melting temperature for Zn-5.0%Al-0.2%Bi alloy are found to be 112.55 J/g, 0.291 J/(g·K), 660.20 K, respectively.
Acknowledgements
This project was supported by Erciyes University Scientific Research Project Unit under Contract No: FYL-2013-4841. The authors are grateful to Erciyes University Scientific Research Project Unit for their financial supports.
References
[1] CUBBERLY W, BAKERJIAN R T. Tool and manufacturing engineers handbook [M]. Dearborn Michigan: Society of Manufacturing Engineers, 1989.
[2] PARK H S, KIMURA T, MURAKAMI T, NAGANO Y, NAKATA K, USHIO M. Microstructures and mechanical properties of friction stir welds of 60%Cu-40%Zn copper alloy [J]. Materials Science and Engineering A, 2004, 37: 160-169.
[3] ANDERSSON C G, ANDREWS R E. Fabrication of containment canisters for nuclear waste by friction stir welding [C]//1st International Symposium on Friction Stir Welding. Thousand Oaks, CA, USA, 1999: 14-16.
[4] SAVASKAN T, TURHAL M S, MURPHY S. Effect of cooling rate on structure and mechanical properties of monotectoid zinc–aluminium alloys [J]. Materials Science and Technology, 2003, 19: 67-74.
[5] PURCEK G, ALTAN B S, MISKIOGLU I, OOI P H. Processing of eutectic Zn-5%Al alloy by equal-channel angular pressing [J]. Journal of Materials Processing Technology, 2004, 148: 279-287.
[6] PRASAD B K. Microstructural alterations through heat treatment and its influence on wear response of a silicon containing zinc based alloy under different test conditions [J]. Materials Science and Technology, 2003, 19: 327-335.
[7] AL-MAHARBI M, KARAMAN I, PURCEK G. Flow response of a severe plastically deformed two-phase zinc–aluminum alloy [J]. Materials Science and Engineering A, 2010, 527: 518-525.
[8]  M, GONZALES F, RAPPAZ M. Growth directions in directionally solidified Al-Zn and Zn-Al alloys near eutectic composition [J]. Scripta Materialia, 2008, 59: 440-443.
M, GONZALES F, RAPPAZ M. Growth directions in directionally solidified Al-Zn and Zn-Al alloys near eutectic composition [J]. Scripta Materialia, 2008, 59: 440-443.
[9] GONZALES F, RAPPAZ M. Dentrite growth directions in aluminum-zinc alloys [J]. Metallurgical and Materials Transactions A, 2006, 37: 2797-2806.
[10] ARESA A E, GUEIJMANB S F, CARAMC R, SCHVEZOV C E. Analysis of solidification parameters during solidification of lead and aluminum base alloys [J]. Journal of Crystal Growth, 2005, 275: 319-327.
[11] YANG C, LI B S, REN M X, FU H Z. Studies of microstructures made of Zn-Al alloys using microcasting [J]. The International Journal of Advanced Manufacturing Technology, 2010, 46: 173-178.
[12] ARESA A E, GASSAC L M, GUEIJMANB S F, SCHVEZOVA C E. Correlation between thermal parameters, structures, dentritic spacing and corrosion behavior of Zn-Al alloys with columnar to equiaxed transition [J]. Journal of Crystal Growth, 2008, 310: 1355-1361.
[13]  W R, FREIRE C M A,
W R, FREIRE C M A,  A. Dentritic solidification microstructure affecting mechanical and corrosion properties of Zn4Al alloy [J]. Journal of Materials Science, 2005, 40: 4493-4499.
A. Dentritic solidification microstructure affecting mechanical and corrosion properties of Zn4Al alloy [J]. Journal of Materials Science, 2005, 40: 4493-4499.
[14]  W R, SPINELLI J E, CHEUNG N, GARCIA A. Secondary dentrite arm spacing and solute redistribution effects on the corrosion resistance of Al-10 wt% Sn and Al-20 wt% Zn alloys [J]. Materials Science and Engineering A: Structural Materials, 2006, 420: 179-186.
W R, SPINELLI J E, CHEUNG N, GARCIA A. Secondary dentrite arm spacing and solute redistribution effects on the corrosion resistance of Al-10 wt% Sn and Al-20 wt% Zn alloys [J]. Materials Science and Engineering A: Structural Materials, 2006, 420: 179-186.
[15] GUPTA A K, KUMAR D R. Formability of galvanized interstitial- free steel sheets [J]. Journal of Materials Processing Technology, 2006, 172: 225-237.
[16] VU T N, MOKADDEM M, VOLOVITCH P, OGLE K. The anodic dissolution of zinc alloys in alkaline solution. II. Al and Zn partial dissolution from 5%Al-Zn coatings [J]. Electrochimica Acta, 2012, 74: 130-138.
[17]  ROMERO N, SALAS O, DELGADO R,
ROMERO N, SALAS O, DELGADO R,  B, URUCHURTU J, MARROCO M, PANOSIAN Z. Evaluating Zn, Al and Al-Zn coatings on carbon steel in a special atmosphere [J]. Construction and Building Materials, 2009, 23: 1465-1471.
B, URUCHURTU J, MARROCO M, PANOSIAN Z. Evaluating Zn, Al and Al-Zn coatings on carbon steel in a special atmosphere [J]. Construction and Building Materials, 2009, 23: 1465-1471.
[18] YADAV A P, KATAYAMA H, NODA K, MASUDA H, NISHIKATA A, TSURU T. Effect of Al on the galvanic ability of Zn-Al Coating under thin layer of electrolyte [J]. Electrochimica Acta, 2007, 52: 2411-2422.
[19] TACHIBANA K, MORINAGA Y, MAYUZUMI M. Hot dip fine Zn and Zn-Al alloy double coating for corrosion resistance at coastal area [J]. Corrosion Science, 2007, 49: 149-157.
[20] HE Y, LI D, WANG D, ZHANG Z, QI H, GAO W. Corrosion resistance of Zn-Al co-cementation coatings on carbon steels [J]. Materials Letters, 2002, 56: 554-559.
[21] MARDER A R. The metallurgy of zinc-coated steel [J]. Progress in Materials Science, 2000, 45: 191-271.
[22] SHIH H C, HSU J W, SUN C N, CHUNG S C. The lifetime assessment of hot-dip 5% Al-Zn coatings in chloride environments [J]. Surface and Coatings Technology, 2002, 150: 70-75.
[23] XU B, PHELAN D, DIPPENAAR R. Role of silicon in solidification microstructure in hot-dipped 55 wt% Al-Zn-Si coatings [J]. Materials Science and Engineering A, 2008, 473: 76-80.
[24] CAHN R W, SIEMERS P A, GEIGER J E, BARDHAN P. The order-disorder transformation in Ni3Al and Ni3Al-Fe alloys: I. Determination of the transition temperatures and their relation to ductility [J]. Acta Metallurgica, 1987, 32: 2737-2751.
[25] HECHT U,  APEL M, WITUSIEWICZ V T, RATKE L, de WILDE J, FROYEN L, CAMEL D, DREVET B, FAIVRE G, FRIES S G, LEGENDRE B, REX S. Multiphase solidification in multicomponent alloys [J]. Materials Science and Engineering R, 2004, 45: 1-49.
APEL M, WITUSIEWICZ V T, RATKE L, de WILDE J, FROYEN L, CAMEL D, DREVET B, FAIVRE G, FRIES S G, LEGENDRE B, REX S. Multiphase solidification in multicomponent alloys [J]. Materials Science and Engineering R, 2004, 45: 1-49.
[26] de WILDE J, FROYEN L, REX S. Coupled two-phase [alpha(Al)+theta(Al2Cu)] planar growth and destabilisation along the univariant eutectic reaction in Al-Cu-Ag alloys [J]. Scripta Materialia, 2004, 51: 533-538.
[27] SNUGOVSKY L, PEROVIC D D, RUTTER J W. Experimental study of Bi-Cd-In phase diagram using conventional methods plus quenching and 'solidification path' techniques [J]. Journal of Materials Science and Technology, 2000, 16: 968-978.
[28] de WILDE J, NAGELS E, LEMOISSON F, FROYEN L. Unconstrained growth along a ternary eutectic solidification path in Al-Cu-Ag: Preparation of a MAXUS sounding rocket experiment [J]. Materials Science and Engineering A, 2005, 413-414: 514-520.
[29] ZHANG L M,  R, GILLE P. Directional solidification studies in complex ternary alloy systems [J]. Journal of Crystal Growth, 2005, 275: 2077-2082.
R, GILLE P. Directional solidification studies in complex ternary alloy systems [J]. Journal of Crystal Growth, 2005, 275: 2077-2082.
[30] BELOV N A,  N N. Constituent phase diagrams of the Al-Cu-Fe-Mg-Ni-Si system and their application to the analysis of aluminium piston alloys [J]. Acta Materialia, 2005, 53: 4709-4722.
N N. Constituent phase diagrams of the Al-Cu-Fe-Mg-Ni-Si system and their application to the analysis of aluminium piston alloys [J]. Acta Materialia, 2005, 53: 4709-4722.
[31] PORTER D A, EASTERLING K E. Phase transformations in metals and alloys [M]. 2nd ed. London: CRC Press, 1992.
[32] JACKSON K A, HUNT J D. Lamellar and rod eutectic growth [J]. Transactions of the Metallurgical Society of AIME, 1966, 236: 1129-1142.
[33] MOORE A, ELLIOTT R. The solidification of metals [C]// Proceeding Joint Conference Iron and Steel Institute. Brighton, 1969: 100-101.
[34] DATYE V, LANGER J S. Stability of thin lamellar eutectic growth [J]. Physical Review B, 1981, 24: 4155-4169.
[35] SEETHARAMAN V, R.TRIVEDI R. Eutectic growth: Selection of interlamellar spacings [J]. Metallurgical Transactions A, 1988, 19: 2955-2964.
[36] TRIVEDI R, MASON J T, VERHOEVEN J D, KURZ W. Eutectic spacing in lead-based alloy systems [J]. Metallurgical Transactions A, 1991, 22: 2523-2533.
[37] OURDJINI A, LIU J, ELLIOTT R. Eutectic spacing selection in Al-Cu system [J]. Journal of Materials Science and Technology, 1994, 10: 312-318.
[38] KAYA H,  M. Eutectic growth of unidirectionally solidified bismuth-cadmium alloy [J]. Journal of Materials Processing Technology, 2007, 183: 310-320.
M. Eutectic growth of unidirectionally solidified bismuth-cadmium alloy [J]. Journal of Materials Processing Technology, 2007, 183: 310-320.
[39] KAYA H,  M. Effect of growth rates and temperature gradients on the spacing and undercooling in broken- lamellar eutectic growth (Sn-Zn eutectic system) [J]. Journal of Materials Engineering and Performance, 2003, 12: 456-469.
M. Effect of growth rates and temperature gradients on the spacing and undercooling in broken- lamellar eutectic growth (Sn-Zn eutectic system) [J]. Journal of Materials Engineering and Performance, 2003, 12: 456-469.
[40] FAVIER J J, de GOER J. Directional solidification of eutectic alloys [C]//European Space Agency Special Publications. ESA SP-222 Paris, 1984: 127-128.
[41] ENGIN S,  U, KAYA H,
U, KAYA H,  N. Directional solidification and physical properties measurements of the zinc-aluminum alloy [J]. International Journal of Minerals Metallurgy and Materials, 2011, 18: 659-664.
N. Directional solidification and physical properties measurements of the zinc-aluminum alloy [J]. International Journal of Minerals Metallurgy and Materials, 2011, 18: 659-664.
[42]  E,
E,  U, KAYA H,
U, KAYA H,  N,
N,  K, AKBULUT S, OCAK Y. The effect of growth rate on microstructure and microindentation hardness in the In-Bi-Sn ternary alloy at low melting point [J]. Journal of Alloys and Compounds, 2009, 470: 150-156.
K, AKBULUT S, OCAK Y. The effect of growth rate on microstructure and microindentation hardness in the In-Bi-Sn ternary alloy at low melting point [J]. Journal of Alloys and Compounds, 2009, 470: 150-156.
[43] WITUSIEWICZ V T, HECHT U, REX S, APEL M. In situ observation of microstructure evolution in low-melting Bi-In-Sn alloys by light microscopy [J]. Acta Materialia, 2005, 53: 3663-3669.
[44]  E, KAYA H,
E, KAYA H,  N. The dependence of lamellar spacings and microhardness on growth rate in the directionally solidified Bi-43 weight pct Sn alloy at a constant temperature gradient [J]. Metals and Materials International, 2009, 15: 741-751.
N. The dependence of lamellar spacings and microhardness on growth rate in the directionally solidified Bi-43 weight pct Sn alloy at a constant temperature gradient [J]. Metals and Materials International, 2009, 15: 741-751.
[45]  A. Interflake spacings and undercoolings in Al-Si irregular eutectic alloy [J]. Materials Science and Engineering: A, 2004, 369: 215-229.
A. Interflake spacings and undercoolings in Al-Si irregular eutectic alloy [J]. Materials Science and Engineering: A, 2004, 369: 215-229.
[46]  M. Effect of growth rates and temperature gradients on the lamellar spacing and the undercooling in the directionally solidified Pb-Cd eutectic alloy [J]. Materials Research Bulletin, 2003, 38: 1457-1466.
M. Effect of growth rates and temperature gradients on the lamellar spacing and the undercooling in the directionally solidified Pb-Cd eutectic alloy [J]. Materials Research Bulletin, 2003, 38: 1457-1466.
[47]  M. Directional solidification and characterization of the Cd-Sn eutectic alloy [J]. Journal of Alloys and Compounds, 2007, 431: 171-179.
M. Directional solidification and characterization of the Cd-Sn eutectic alloy [J]. Journal of Alloys and Compounds, 2007, 431: 171-179.
[48] TRIVEDI R, MAGNIN P, KURZ W. Theory of eutectic growth under rapid solidification conditions [J]. Acta Metallurgica, 1987, 35: 971-980.
[49] CLARK J N, ELLIOTT R. Lamellar spacings in the tin-cadmium eutectic [J]. Journal of Crystal Growth, 1976, 33: 169-173.
[50] BORLAND S M D, ELLIOTT R. Growth temperatures in Al-CuAl2 and Sn-Cd eutectic alloys [J]. Metallurgical Transactions A, 1978, 9: 1063-1067.
[51] JORDAN R M, HUNT J D. The growth of lamellar eutectic structures in the Pb-Sn and Al-CuAl2 systems [J]. Metallurgical Transactions A, 1971, 2: 3401-3410.
[52] KHAN S, OURDJINI A, HAMED Q S, NAJAFABADI M A A, ELLIOTT R. Hardness and mechanical property relationships in directionally solidified aluminium-silicon eutectic alloys with different silicon morphologies [J]. Journal of Materials Science, 1993, 28: 5957-5962.
[53] VNUK F, SAHOO M, MERWE V R, SMITH R W. The hardness of Al-Si eutectic alloys [J]. Journal of Materials Science, 1979, 14: 975-982.
[54] GROBNER J, MIRKOVIC D, SCHMID-FETZER R. Monotectic four-phase reaction in Al-Bi-Zn alloys [J]. Acta Materialia, 2005, 53: 3271-3280.
[55]  M. The dependence of lamellar spacing on growth rate and temperature gradient in the lead-tin eutectic alloy [J]. Journal of Materials Processing Technology, 2000, 97: 74-81.
M. The dependence of lamellar spacing on growth rate and temperature gradient in the lead-tin eutectic alloy [J]. Journal of Materials Processing Technology, 2000, 97: 74-81.
[56]  Directional solidification of Al-Cu-Ag alloy [J]. Applied Physics A, 2009, 95: 923-932.
Directional solidification of Al-Cu-Ag alloy [J]. Applied Physics A, 2009, 95: 923-932.
[57] RUDNEV V, LOVELESS D, COOK R, BLACK M. Handbook of Induction Heating [M]. New York: Markel Dekker Inc, 2003.
[58] HANSEN M, ANDERKO K. Constitutions of binary alloys [M]. New York: Mc Graw-Hill Book Company, 1958.
[59] MUNITZ A. Microstructure of rapidly solidified laser molten Al-4.5 wt pct Cu surfaces [J]. Metallurgical Transactions B, 1985, 16: 149-161.
[60] ZIMMERMANN M, CARRARD M, KURZ W. Rapid solidification of Al-Cu eutectic alloy by laser remelting [J]. Acta Metallurgica, 1989, 37: 3305-3313.
[61] CHEUNG N,  The use of artificial intellligence for the optimisation of a laser transformation hardening process [J]. Lasers in Engineering, 2000, 10: 275-291.
The use of artificial intellligence for the optimisation of a laser transformation hardening process [J]. Lasers in Engineering, 2000, 10: 275-291.
[62]  W R, GARCIA A. Modeling dendritic structure and mechanical properties of Zn-Al alloys as a function of solidification conditions [J]. Materials Science and Engineering A, 2002, 325: 103-111.
W R, GARCIA A. Modeling dendritic structure and mechanical properties of Zn-Al alloys as a function of solidification conditions [J]. Materials Science and Engineering A, 2002, 325: 103-111.
[63] QUARESMA J, SANTOS C A, GARCIA A. Correlation between unsteady state solidification conditions dendrite spacings and mechanical properties of Al-Cu alloys [J]. Metallurgical Transactions A, 2000, 31: 3167-3178.
[64] SIQUEIRA C, CHEUNG N, GARCIA A. Solidification thermal parameters affecting the columnar-to equiaxed transition [J]. Metallurgical and Materials Transactions A, 2002, 33: 2107-2118.
[65] HALL E O. The deformation and ageing of mild steel: III discussion of results [J]. Proceedings of the Physical Society Section B, 1951, 64: 747-753.
[66] PETCH N J. The cleavage strength of polycrystals [J]. Journal of the Iron and Steel Institute, 1953, 174: 25-28.
[67] PRASAD B K, MODI O P. Slurry wear characteristics of zinc-based alloys: Effects of sand content of slurry, silicon addition to alloy system and traversal distance [J]. Transactions of Nonferrous Metal Society of China, 2009, 19: 277-286.
[68]  T, MURPHY S. Dry sliding friction and wear properties of zinc-based alloys [J]. Wear, 2002, 252: 894-901.
T, MURPHY S. Dry sliding friction and wear properties of zinc-based alloys [J]. Wear, 2002, 252: 894-901.
[69] LIN Gao-yong, ZHANG Rui, WANG Li, LEI Yu-xia, HE J J. Effects of stabilizing heat treatment on microstructures and creep behavior of Zn-10Al-2Cu-0.02Ti alloy [J]. Transactions of Nonferrous Metal Society of China, 2013, 23: 86-91.
[70]  N. Variation of microindentation hardness with solidification and microstructure parameters in the Al based alloys [J]. Applied Surface Science, 2008, 255: 3071-3078.
N. Variation of microindentation hardness with solidification and microstructure parameters in the Al based alloys [J]. Applied Surface Science, 2008, 255: 3071-3078.
[71] KAYA H,  E, UZUN O. Effect ofgrowth rate and lamellar spacing on microhardness in the directionally solidified Pb-Cd, Sn-Zn and Bi-Cd eutectic alloys [J]. Journal of Materials Science, 2004, 39: 6571-6576.
E, UZUN O. Effect ofgrowth rate and lamellar spacing on microhardness in the directionally solidified Pb-Cd, Sn-Zn and Bi-Cd eutectic alloys [J]. Journal of Materials Science, 2004, 39: 6571-6576.
[72] LAPIN J,  L, NAZMY M. Directional solidification of intermetallic Ti-46Al-2W-0.5Si alloy in alumina moulds [J]. Intermetallics, 2002, 10: 1019-1031.
L, NAZMY M. Directional solidification of intermetallic Ti-46Al-2W-0.5Si alloy in alumina moulds [J]. Intermetallics, 2002, 10: 1019-1031.
[73]  E,
E,  M. Investigation of mechanical, electrical, and thermal properties of a Zn-1.26 wt% Al alloy [J]. Journal of Materials Science, 2011, 46: 1414-1423.
M. Investigation of mechanical, electrical, and thermal properties of a Zn-1.26 wt% Al alloy [J]. Journal of Materials Science, 2011, 46: 1414-1423.
[74] HULTGREN R, ORR R L, ANDERSON P D, KELLEY K K. Selected values of thermodynamic properties of metals and alloys [M]. Berkeley: John Wiley & Sons Inc, 1963.
Yasin KARAMAZI1,  BAYRAM2,
BAYRAM2,  ATA3, Sezen
ATA3, Sezen  4,
4, 
 2, Necmettin
2, Necmettin  5
5
1. Department of Physics, Institute of Science and Technology, Erciyes University, Kayseri 38039, Turkey;
2. Department of Physics, Faculty of Science, Erciyes University, Kayseri 38039, Turkey;
3. Department of Physics, Institute of Science and Technology,  50300, Turkey;
50300, Turkey;
4. Department of Physics, Faculty of Arts and Sciences,  50300, Turkey;
50300, Turkey;
5. Department of Metallurgical and Materials Engineering, Faculty of Chemistry and Metallurgical Engineering,  34220, Turkey
34220, Turkey
摘 要:采用Bridgman型定向凝固炉在一定温度梯度和不同生长速率下制备Zn-5%Al-0.2%Bi(质量分数)合金。测量了定向凝固Zn-Al-Bi合金的枝晶间距、显微硬度、抗拉强度和电阻率。采用线性回归分析研究生长速率对合金枝晶间距、显微硬度、抗拉强度和电阻率的影响。在低生长速率下(小于450.0 μm/s),所得结果与在相似生长速率下定向凝固的Zn-Al合金的结果吻合,但与Jackson-Hunt共晶理论和高生长速率下的实验结果不同。Zn-Al-Bi共晶合金的临界生长速率为450 μm/s。从热流-温度曲线中可以得到,Zn-Al-Bi合金的熔化焓、固液相比热差以及熔化温度分别为112.55 J/g、0.291 J/(g·K)和660.20 K。
关键词:定向凝固;锌铝合金;显微组织;显微硬度;拉伸强度;电学性能
(Edited by Yun-bin HE)
Corresponding author: Necmettin  ; Tel: +90-212-383-46-84; Fax: +90-212-383-46-65; E-mail: nmarasli@yildiz.edu.tr
; Tel: +90-212-383-46-84; Fax: +90-212-383-46-65; E-mail: nmarasli@yildiz.edu.tr
DOI: 10.1016/S1003-6326(16)64354-6

