Trans. Nonferrous Met. Soc. China 29(2019) 1956-1966

Germanium transport across supported liquid membrane with Cyanex 923: Mathematical modeling

Hossein KAMRAN HAGHIGHI¹, Mehdi IRANNAJAD¹, Ana MARIA SASTRE²

1. Department of Mining and Metallurgical Engineering, Amirkabir University of Technology, Tehran, Iran;

2. Department of Chemical Engineering, Universitat Politecnica de Catalunya, ESTEIB, Av. Diagonal 647, 08028 Barcelona, Spain

Received 19 December 2018; accepted 25 April 2019

Abstract: A mathematical model was developed to monitor the facilitated transport of germanium(IV) from oxalic acid solutions through a flat sheet supported liquid membrane (FSSLM) containing four trialkylphosphine oxides (Cyanex 923). The FSSLM modeling was based on the extraction constant (K_ext) calculated from the liquid-liquid extraction (LLX) modeling. The LLX model presented a reliable calculation of the extraction constant (K_ex= 2.057×10³ L/mol⁴). The FSSLM model was solved using Matlab software according to extraction constant, Fick’s law, and diffusional principles. The model predicts the overall mass transfer coefficient (K_org) to be 3.84 cm/s. Using this value, diffusion coefficients (D_m) for various Cyanex 923 concentrations of 0.126, 0.252, 0.378, 0.505, 0.631 and 0.757 mol/L are found to be 8.50×10^-4, 4.30×10^-4, 1.87×10^-4, 5.87×10^-5, 2.57×10^-5, 2.09×10^-5 cm²/s, respectively. The results show that the diffusion rate of the current study is approximately more than that of similar FSSLM systems containing Cyanex 923 used to transport various metals. The modeling values are in good agreement with the experimental data, showing the good reliability of the mathematical model.

Key words: supported liquid membrane; Cyanex 923; germanium; transport; mathematical modeling

1 Introduction

The role of germanium in strategic applications such as semiconductors, catalysts, fiber optics, and alloys, has caused companies and countries to recover and use it [1-4]. Important primary resources of germanium are classified into zinc sulfide ores [4] and fly ashes [5]. Leachates or wastewaters released from plant processing the mentioned materials may contain germanium. In order to separate germanium from these effluents, various techniques have been developed [4]. Liquid-liquid extraction (LLX) [6], ion exchange [7], ion flotation [8], adsorption [9], precipitation [10], and emulsion liquid membrane (ELM) [1] are some of these techniques applied to separating germanium from aqueous solutions. Liquid membrane separation is a type of technique combining the extraction and stripping stages of liquid-liquid extraction processes in a single step. Some advantages such as energy saving, low investment and operational cost due to the lower consumption of extractants have made this technique to be effective in industrial usages [11-13]. Bulk LM (BLM), supported LM (SLM), polymer inclusion membrane (PIM) and emulsion LM (ELM) are various types of developed membranes. In flat sheet SLM techniques, a membrane impregnated in a carrier, i.e. commonly a hydrophobic membrane, transports species from a feed phase to a receiving/strip phase based on the chemical potential gradient [11,14-16].

Mathematical modeling helps to recognize the application and performance of SLM systems [17]. It can be useful for designing an effective operation and scaling up SLM systems [18]. The modeling of ion transport through a liquid membrane is carried out according to one of the following assumptions: (1) considering diffusion layers existing in the organic- aqueous interface [11], (2) considering that an organic molecule (carrier) leaves the membrane phase and reacts with aqueous species in the aqueous phase [19], and (3) ignoring the presence of static layers formed between the liquid membrane and aqueous phase existing in the feed and strip sides [20]. The third assumption has been considered to develop a mathematical model in the present study. In this assumption, only the diffusion across SLM has taken place in the system. It is noted that an appropriate agitation of the feed/strip phases is necessary to eliminate the aforementioned interfacial layer. In the current study, a developed SLM system with well-designed impellers was used to eliminate the interfacial layers.

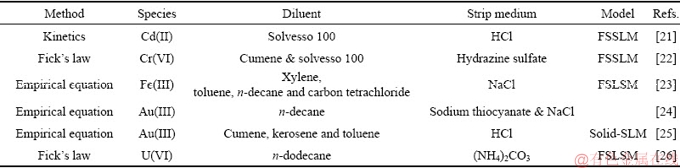
Several works studied the transport modeling of various species using Cyanex 923 as a carrier. Table 1 shows a summary of these studies.

A kinetic model was obtained to describe parameters of the cadmium transport, including diffusions of ions, carrier, and carrier-ions across diffusion layers and interfacial chemical reactions [21]. ALGUACIL and ALONSO [22] found the flux of chromium transported using Cyanex 923 in an FSSLM system with the basis of a model calculated using the Fick’s law. A permeation model illustrating the facilitated transport mechanism of iron(III) across a liquid membrane impregnated in Cyanex 923 was developed by ALGUACIL and MARTINEZ [23]. Mass transfer resistances and diffusion coefficients were found using this model. The transport model of gold(III) across an SLM using Cyanex 923 diluted in n-decane was used to find resistances and diffusion coefficients [24]. Another model was developed to predict the membrane phase composition containing PC88A and Cyanex 923 in the physicochemical transport of uranium(VI) [26]. A mathematical model showing the transport rate was developed by SASTRE et al [25]. Based on this model, equations in which a relationship was found between the permeability coefficient and equilibrium parameters as well as the concentrations of reagents were described. Furthermore, parameters such as diffusion resistances were calculated by means of the aforementioned model. Similarly, KAMRAN HAGHIGHI et al [27] developed a mass transfer model to find transport resistances existing in the membrane phase and the boundary interface layer.

The aim of this work is modeling the germanium(IV) facilitated transport from neutral media using an organophosphorus carrier called Cyanex 923. The development of a mathematical model for the germanium(II) liquid-liquid extraction resulted in determining the extraction equilibrium constant. This constant was the basis of FSSLM modeling. Using this constant, another mathematical model was developed according to the extraction equilibrium equation, Fick’s law, and diffusional transport to image the behavior of germanium transport across the membrane. The diffusion and transport parameters were found using this model. The goodness of the obtained models was evaluated by comparing the correlations of experimental and model data.

2 Experimental

An organophosphorus organic extractant called Cyanex 923 (four trialkylphosphine oxides) with the composition of 93 wt.% was provided by CYTEC Inc., USA. In all experiments, kerosene from Sigma-Aldrich was used as a diluent to dissolve Cyanex 923. A synthetic solution was prepared by dissolving germanium(IV) dioxide (GeO₂) with the purity of 99.998% (Sigma- Aldrich A.C.S. Reagent) in distilled water. The oxalic acid powder (Panreac, Barcelona, Spain) was used to convert germanium to neutral germanium oxalate species. The other reagents used were analytical grade from Merck, Germany.

In order to find the extraction equilibrium constant of the LLX system, a series of experiments were conducted by shaking organic and aqueous phases with O:A ratio of 1 in separatory funnels by means of a mechanical shaker (SBS Instruments SA, Spain). The time of each experiment was 15 min followed by separating aqueous and organic phases. After the phase separation, a 0.5 mL sample from the aqueous phases was taken to be analyzed by means of an inductively coupled plasma (ICP) (Agilent 700 Series, US). It is noted that the germanium concentration of organic phases was found by mass balancing. All aqueous phases used in the experiments contained 100 mg/L Ge and oxalic acid of 0.1 mol/L (pH=0.8±0.1). Furthermore, the Cyanex 923 composition as the carrier was varied in the range of 1-30 vol.% (0.025 to 0.757 mol/L).

Table 1 Summary of literature survey on species transport modeling using Cyanex 923

FSSLM experiments were conducted in two cells (with volume of 220 mL) with a flanged space between them in which a membrane filter was set. The effective area of the membrane was calculated to be 11 cm². The detailed configuration was represented elsewhere [28]. The liquid membrane of this study contains Cyanex 923 in the range of 5-30 vol.% (0.126 to 0.757 mol/L) as the carrier and the PTFE sheet as the membrane support. The membrane used was a Millipore Durapore poly tetra fluoro ethylene (PTFE) membrane with a diameter of 47 mm and a pore size of 0.45 μm. The porosity, membrane thickness, and tortuosity of this membrane were 85%, 30 μm, and 1.18, respectively [29]. To prepare the system, the PTFE membrane was soaked in Cyanex 923 (with various concentrations) dissolved in kerosene for 1 h. The pores of the membrane were properly occupied with the carrier solution by capillarity. Subsequently, the soaked membrane was removed from carrier solutions and rinsed with pure distilled water to eliminate excess carriers. Finally, the membrane was placed between two cells. As mentioned before, in order to eliminate the interfacial layers, solutions in the cells were efficiently agitated with well-organized mechanical impellers. The mixing speed of mechanical impellers was kept at 1300 r/min. According to literature, with an increase of the mixing speed up to 1000 r/min, the thickness of interfacial layers close to the membrane is minimized and can be ignored [30,31]. In each experiment, 0.5 mL samples were taken from feed/ receiving phases at desired durations followed by analyzing the germanium concentration of the solution by means of ICP (Agilent 700 Series). The reproducibility of experimental values was found in the range of ±5% and has been shown as error bars in related figures. Since the kinematic viscosity was used in FSSLM modeling, it was calculated for various concentrations of Cyanex 923 using a “capillary U-tube viscometer” supplied from SCHOTT Instruments. The constant viscometer was determined to be 0.01 by the supplier. Calculations were carried out on the basis of the ASTM D445 standard. In order to find the kinematic viscosity, transport time for various concentrations of the carrier was multiplied by the mentioned constant. To evaluate the dynamic viscosity, kinematic values were multiplied by the corresponding density.

3 Modeling

3.1 Liquid-liquid extraction

In order to model the extraction of germanium from a solution containing oxalic acid, a series of mass balance and chemical equilibrium equations were considered. In the equilibrium condition, equations corresponding to species reacted in aqueous and organic phases were obtained. In order to obtain these equations, the germanium extraction mechanism of Cyanex 923 from a solution containing oxalic acid should be described. Since Cyanex 923 extracts species as the solvation mechanism, it is predicted that neutral species of germanium are extracted. With respect to the previous works, neutral species of trisoxalato germanates formed in aqueous solutions as in Eq. (1) [5]:

3H₂C₂O₄+GeO₂·H₂OH₂Ge(C₂O₄)₃+3H₂O (1)

The aim of modeling for the LLX system was to find the extraction equilibrium constant used in FSSLM modeling. For this purpose, a series of experiments were conducted in the carrier concentrations of 1-30 vol.%. The overall reaction between trisoxalato germanates and Cyanex 923 can be written as Eq. (2) [5]:

H₂Ge(C₂O₄)_3aq+4L_orgH₂Ge(C₂O₄)₃·4L_org (2)

Subscripts aq and org represent aqueous and organic phases, respectively. The extraction equilibrium constant for this reaction is written as Eq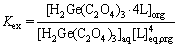. (3):

(3)

where brackets show the concentration and eq subscript depicts the equilibrium condition. In order to simplify the mathematical formulas, [L]_eq, [H₂Ge(C₂O₄)₃·4L]_org, and [H₂Ge(C₂O₄)₃]_aq are replaced with L_eq, C_Ge,org,i, and C_Ge,aq.exp,i, respectively. Obtaining K_ex was carried out based on minimizing the sum of squares (SS) attained between the experimental and modeling extraction efficiencies. The corresponding calculations were conducted using the solver technique in Excel 2016 software. For this purpose, solver dedicated a value to K_ex. Using this value, the germanium concentration in the organic phase was again calculated using Eq. (3). Then, the model extraction efficiency can be found using Eq. 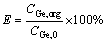(4).

(4)

where E_model and E_exp are the extraction efficiencies obtained from the model and experiments. Finally, the sum of square values based on extraction efficiencies of experiments and model were obtained as Eq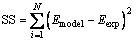. (5):

(5)

where i and N depict counter and the number of experiments, respectively. The mentioned dedication continued until the best K_ex was found in a condition in which SS between the model and experimental values were minimum.

3.2 Flat sheet supported liquid membrane

As mentioned before, the extraction equilibrium constant (K_ex) of the LLX system found using the corresponding model was used in the formulation of the FSSLM system. Matrixes were used in the mathematical programming in the Matlab software as follows:

(1) A matrix includes columns of the germanium initial concentration, Cyanex 923 concentration, the number of samples in each carrier concentration, and the corresponding viscosities.

(2) A time matrix includes times of the taken samples in each condition (i which shows the initial concentration of the carrier) imported in each row.

(3) A matrix called the concentration matrix containing the germanium concentrations of the feed solution at times mentioned in the time matrix.

Resistances in the interfacial layers have been ignored during the modeling due to the good agitation of solutions by impellers placed close to the membrane phase. According to the literature, the interfacial resistances are usually ignored in rough models [32]. In the present study, the model was created based on the Fick’s law as in Eqs. (6) and (7):

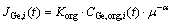(6)

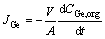(7)

where J_Ge is the germanium flux through the membrane, K_org represents an overall mass transfer coefficient; μ is the dynamic viscosity, α is a constant value representing the power of the carrier’s viscosity, V is the volume equal to 220 mL and A is the membrane effective area equal to 11 cm². For easiness, the germanium concentration transported by Cyanex 923 was represented with C_Ge,org,i. In order to create a model, the Matlab 2012 software was used to write a program as shown in Fig. 1 and the following procedures:

(1) The concentration of germanium transported (C_Ge,org,i(t)) by Cyanex 923 with a specific concentration (i, e.g. i=1 represents the concentration of 5 vol.%) was calculated at the time of t with respect to the experimental germanium concentration of the feed phase (C_Ge,aq,exp,i) as the extraction equilibrium reaction represented in Eq. (3). This calculation is as Eq. (8):

(8)

(2) In each loop, fmincon generated values for K_org and α. Using these values, J_Ge(t) was calculated using Eq. (6). The calculated germanium concentration (C_Ge,aq,cal,i(t)) in the feed phase at the time of t in various experimental conditions (i) was obtained using Eq. (7) and rewritten as Eq. (9):

(9)

In this equation, C_Ge,aq,cal,i(t-1) depicts the germanium concentration in the feed solution at the time of t-1. Furthermore, △t is the time interval of the calculations (here △t is 1 min).

Fig. 1 Flowchart of modeling procedure used to develop FSSLM model of this study

(3) The objective values of this study are K_org and α. Their optimum values were found based on minimization of the sum of squares using the fmincon function (see Fig. 1). After obtaining values of calculated germanium concentrations for a loop (C_Ge,aq,cal,i(t)), the sum of the square (SS) function was calculated from the squared differences between the calculated and experimental values as Eq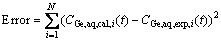. (10):

(10)

(4) If the error function was minimized, the objective values of K_org and α produced using fmincon would be optimized, otherwise, new values were generated to continue calculations according to the aforementioned procedures.

4 Results and discussion

4.1 Liquid-liquid extraction

The LLX system was modeled to find the extraction equilibrium constant based on minimizing the sum of squares (SS) for differences between experimental and calculated extraction efficiencies according to the procedure mentioned in the modeling section. To construct the model, experimental parameters such as the carrier concentration, the initial concentration of germanium, and the experimental results such as the extraction efficiency are required. Table 2 illustrates the initial conditions of experiments at room temperature used for modeling.

Table 2 Initial conditions of LLX system at room temperature used for modeling

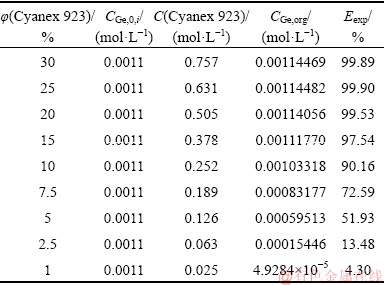
The solver method tried to find a K_ex value by which the sum of squares function was minimized. In each step, a proposed K_ex was used to calculate the concentration of germanium in the organic solution using Eq. (8) followed by evaluating a value for the extraction efficiency using Eq. (4) called the calculated extraction efficiency (E_cal). Finally, using the optimum value of K_ex, the SS value was found. According to the results, a value of 2056.83 L/mol⁴ was obtained for the extraction equilibrium constant of the Cyanex 923 solvent extraction system. In addition, the value of 3.83×10^-3 was found for the minimized SS function which shows that the difference between each experimental point and the curve of the best fit is very low. In order to evaluate the accuracy of the LLX model, the plot of extraction efficiency vs. the extractant concentration was constructed as shown in Fig. 2. According to this figure, the trend of both the model and experimental data represents the enhancement of the extraction efficiency with an increase of the extractant concentration up to an unchanged level (after the point corresponding to 15 vol.% Cyanex) in which the maximum extraction is obtained. In addition, this figure shows that the model curve has a good fit to the experimental points. The plot of the model extraction efficiency versus experimental results and the regression line show a correlation coefficient of 0.96, indicating that model values are close to the values obtained from the experiments. Since a specific membrane was used in all experiments with Cyanex 923, the value of K_ex obtained in the LLX system can be used in the SLM system. This supposition is usually considered in similar modeling [33].

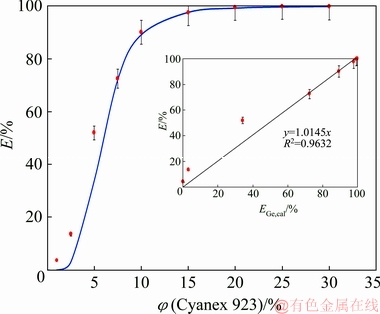
Fig. 2 Model and experimental extraction efficiencies obtained in LLX system versus Cyanex 923 concentration and regression line showing correlation of experimental and model data (insert)

4.2 Flat sheet supported liquid membrane

In order to model the germanium transport across the PTFE membrane containing Cyanex 923, the extraction equilibrium constant, the equilibrium reaction, Fick’s law, and diffusional principles were used. Considering that the germanium distribution coefficient between the membrane and stripping phases is much lower than that between the feed and membrane phases, the concentration difference between the strip and feed sides may be negligible. This supposition is based on liquid-liquid extraction experiments in which germanium is extracted very fast with Cyanex 923 and then stripped with NaOH. Experimental data used for the construction of the FSSLM model are listed in Table 3. Figure 1 showed the procedure used in modeling.

Table 3 Initial conditions used for developing model for FSSLM in this study

The goal of FSSLM modeling was to find germanium diffusion parameters controlling the transport process. As seen in Table 3, various concentrations of Cyanex 923 in the range of 5%-30% were used in the PTFE membrane. According to Fig. 1, the germanium concentration in the feed phase and related times were used in the modeling process. In order to follow the instructions shown in Fig. 1 and introduced in the “Modeling” section, a series of program codes were written in Matlab R2014b software. As seen in this figure, modeling was carried out in two loops; first, a loop corresponding to time placed within the main loop, in which the germanium concentration was calculated for each minute and a specific condition (i=Cyanex 923 concentration), second, the main loop for changing i. For comparing the calculated values with the experimental ones, model germanium concentrations corresponding to times of experimental points were kept. Finally, the objective values were found when the error function was minimized.

The mass transfer process in the presented SLM process occurs in several steps: first, the diffusion of germanium oxalates and protons from the feed bulk to the inner part of the membrane, second, the reaction of diffused species and Cyanex 923, then, transport of germanium-Cyanex 923 species across the membrane, afterward, the detachment of germanium from Cyanex 923 using NaOH as a strip solution, and finally, the inverse transport of carrier molecules toward the feed phase. For better understanding, the overall mass transfer coefficient (K_org) has been defined with respect to Eq. (6), which can be found by the program. This value is used to quantify the mass transfer phenomena and helps to understand which carrier concentration has better transport rate. In addition, the selection of an optimized system can be possible using this quantified coefficient. According to results, this value was found to be 3.84 cm/s. Furthermore, the power of the carrier’s viscosity was obtained to be 0.60. HISS and CUSSLER [34] reported that the power of the carrier’s viscosity for a viscous solvent is about 2/3. This agreement between the values can confirm the accuracy of the model. Moreover, the values of the mass transfer coefficient (K_m) corresponding to different carrier concentrations can be obtained by multiplying the overall mass transfer coefficient by μ^-α. Using the mass transfer coefficient for each carrier concentration, the diffusion coefficient (D_m) can be calculated using the equation reported by PRASAD and SIRKAR [35] as Eq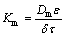. (11):

(11)

In this equation, porosity, membrane thickness, and tortuosity are shown by ε, δ, and τ, respectively. The values of D_m calculated using Eq. (11) are illustrated in Table 4.

Table 4 Values of mass transfer and diffusion coefficients for various concentrations of Cyanex 923 in FSSLM system

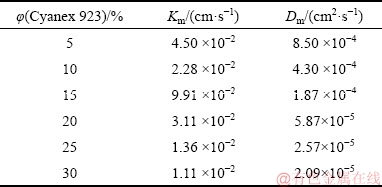
As seen in Table 4, the values of D_m decreased with increasing Cyanex 923 concentration. This decrease possibly occurs due to an enhancement of the carrier viscosity. Diffusion coefficients (D_m) obtained were compared with D_m of the other FSSLM systems containing Cyanex 923 used to transport various species. Table 5 illustrates this comparison.

As seen in Table 5, in the Fe-Cyanex 923 (0.252 mol/L) system, first K_ex was calculated and then diffusion rates of iron species across the feed diffusion layer-membrane were used to calculate the rate of the Fe(III) transport. Using these rates, the Fick’s first law was applied to finding the iron flux through the membrane. The model parameters being the aqueous and organic resistances were found followed by calculating the diffusion coefficient using the obtained organic resistance [23]. Moreover, ALGUACIL et al [24] developed a similar model for the facilitated transport of gold(III) using Cyanex 923 across a PVDF membrane with 125 μm in thickness, the porosity of 75% and pore size of 22 μm. In the above-mentioned studies, Fe(III) and Au(III) were transported as HFeCl₄ and HAuCl₄ from chloride media using Cyanex 923. In a model developed by ALGUACIL and ALONSO [22], diffusional fluxes of Cr(IV) at interfacial layers and the membrane phase were determined by two equations. These fluxes had a relationship with corresponding diffusion coefficients. The carrier and the membrane were Cyanex 923 and PVDF with characteristics similar to that explained for the Au-Cyanex 923 system. ALONSO et al [21] used diffusion rates of cadmium transport through the feed diffusion layer and the membrane to evaluate the transport rate and to model the facilitated transport of cadmium species through a PVDF membrane using Cyanex 923. The procedures used in the mentioned study were similar to those reported by ALGUACIL and MARTINEZ [23]. Since three types of cadmium species namely CdCl₂, HCdCl₃, and H₂CdCl₄ existed in the aqueous solutions, three K_ex values were calculated and used to calculate diffusional flux equations. The values obtained in the aforementioned studies are listed in Table 5. As seen in this table, most D_m values are lower than those obtained in the current study. However, the D_m value of the Cr-Cyanex 923 (0.505 mol/L) system is slightly higher than that of this study. Therefore, this result indicates the high germanium diffusivity through the PTFE membrane containing Cyanex 923.

Table 5 Evaluation of diffusion coefficients in references

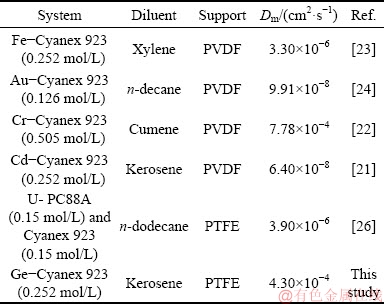
The validity of the model was determined by comparing the experimental and calculated data. In this regard, a series of plots corresponding to calculated and experimental results were plotted. Plots were constructed for six Cyanex 932 concentrations mentioned in Table 3. Figure 3 illustrates plots of germanium concentration in the feed phase obtained from experimental and model results as a function of time. The continuous lines and the circular points depict the calculated and experimental data, respectively. With respect to these plots, the germanium concentration decreased in the feed phase over time, meaning that the transport of these species occurred through the FSSLM. With respect to the model curves of (c)-(f), the germanium concentration reached a steady state at the approximate time of 1350 min which indicated that the transport rate was enhanced with an increase of the Cyanex 923 concentration and then reached a steady state. Hence, it can be concluded that at the Cyanex 923 concentrations above 0.378 mol/L (15 vol.%), there is not a significant variation in the transport rate. As mentioned before, the viscosity increases with an enhancement of the carrier concentration which results in enhancing the membrane resistance and decreasing the diffusivity of the Ge–Cyanex 923 complexes. With respect to the inverse relationship of the diffusion coefficient and the viscosity, this decrease can be understood [36]. In addition, it has been reported that the species extraction by the carrier within the porous membrane can decrease the availability to reactive sites [37,38].

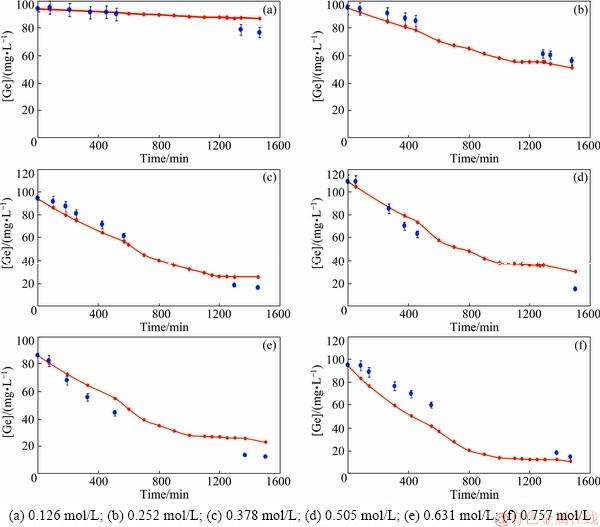
Fig. 3 Model and experimental concentrations of germanium in feed phase versus time for different Cyanex 923 concentrations

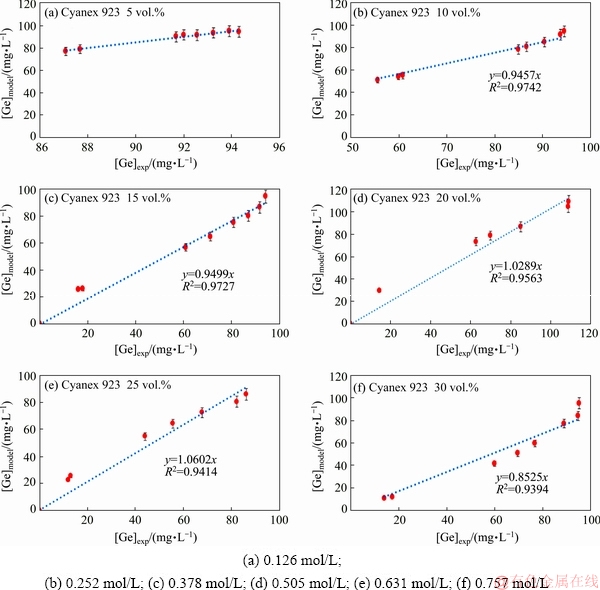
Fig. 4 Regression lines showing correlation of experimental and model data for different Cyanex 923 concentrations

The inclination of the experimental points to the model curves shows the accuracy of model points to experimental ones. As seen in Fig. 3(a), the transport rate corresponding to the Cyanex 932 concentration of 0.126 mol/L is very low, as less than 10% of germanium is transported after 1468 min. However, in the mentioned plot, the model curves have a good tendency to the experimental points. In other carrier concentrations, the transport rates were gradually increased. Another way to investigate the model accuracy is to show the correlations between experimental and calculated data. This purpose was carried out by plotting the calculated concentrations as a function of experimental results (Fig. 4). According to this figure, correlation coefficients are higher than 94%, showing a good agreement between experimental and model data. With respect to the literatures, values for correlation coefficients above 0.9 show a good fit with the high correlation in a regression plot [39,40]. However, since the transport of germanium corresponding to the Cyanex 923 concentration of 0.126 mol/L is very low, the correlation line could not intercept the origin. Thus, the corresponding correlation coefficient could not be obtainable.

5 Conclusions

(1) A mathematical model was developed to facilitate the transport of Ge(IV) from oxalic acid solutions across FSSLM composed of the Cyanex 923 and a PTFE disc membrane. This model was based on an LLX model, by which the extraction equilibrium constant was found (K_ex=2057 L/mol⁴).

(2) The FSSLM model curves fitted the results obtained from FSSLM experiments for various carrier concentrations. This model resulted in determining the overall mass transfer and diffusion coefficients for the PTFE membranes containing 0.126, 0.252, 0.378, 0.505, 0.631, and 0.757 mol/L Cyanex 923.

(3) With respect to results, it was possible to fit the model curves to experimental extraction data for all carrier concentrations. As a result, a good agreement between the model and experimental data showed the accuracy of the model.

(4) The model can be applied for depth understanding the processes occurring during the facilitated transport of germanium. Moreover, the mentioned models can be valuable for further investigation and designation of hollow-fibre SLM and LLX processes.

Acknowledgments

This study was performed in the Department of Chemical Engineering, Universitat Politecnica de Catalunya, Vilanova i la Geltrú Campus, Spain. The authors wish to acknowledge Dr. Agustin Fortuny and Dr. Maria Teresa Coll for their help and scientific advice.

Symbols

A

Membrane effective area, cm²

C_Ge,aq,0

Initial concentration of germanium in the feed phase, mol/L

C_Ge,cal,aq,i(t)

Calculated (model) concentration of germanium in the feed phase at the time of t, mol/L

C_{Ge, exp,aq,i}(t)

Experimental concentration of germanium in the feed phase at the time of t, mol/L

C_Ge,org,i

Concentration of germanium in the organic phase in LLX system, mol/L

J_Ge

Flux of germanium, mol/(s·cm²)

i

Condition number

K_org

Overall mass transfer coefficient, cm/s

K_ex

Extraction equilibrium constant, L/mol⁴

L_eq

Equilibrium concentration of Cyanex 923, mol/L

N_exp

Number of experiments

N_exp,maximum

Final number of experiments

N_time

Number of samples taken at individual time

L_0,i

Initial concentration of Cyanex 923 at the condition of i, mol/L

[T ]

Matrix containing time in which samples were taken

t_f

Final time in which a sample was taken, min

V

Volume of phase, mL

μ_i

Dynamic viscosity of carrier with various concentration, mm²/s

α

Power of carrier’s viscosity

ε

Porosity

σ

Membrane thickness, μm

τ

Tortuosity

References

[1] LIU F, YANG Y, LU Y, SHANG K, LU W, ZHAO X. Extraction of germanium by the AOT microemulsion with N235 system [J]. Industrial & Engineering Chemistry Research, 2010, 49: 10005-10008.

[2] YOON J W, PARK J K, KIM K H, KANG M C, CHO S H. Internal modification in transparent hybrid germanium-silica plates using plasma formation induced by a femtosecond laser [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(S): s808-s812.

[3] NIU Z W, HUANG J H, CHEN S H, ZHAO X K. Effects of germanium additions on microstructures and properties of Al-Si filler metals for brazing aluminum [J]. Transactions of Nonferrous Metals Society of China, 2016, 26: 775-782.

[4] ZHOU Z A, CHU G, GAN H X, YANG T Z, CHEN L. Ge and Cu recovery from precipitating vitriol supernatant in zinc plant [J]. Transactions of Nonferrous Metals Society of China, 2013, 23: 1506-1511.

[5] KAMRAN HAGHIGHI H, IRANNAJAD M, FORTUNY A, SASTRE A M. Recovery of germanium from leach solutions of fly ash using solvent extraction with various extractants [J]. Hydrometallurgy, 2018, 175: 164-169.

[6] KUROIWA K, OHURA S I, MORISADA S, OHTO K, KAWAKITA H, MATSUO Y, FUKUDA D. Recovery of germanium from waste solar panels using ion-exchange membrane and solvent extraction [J]. Minerals Engineering, 2014, 55: 181-185.

[7] TORRALVO F A, FERNANDEZ-PEREIRA C. Recovery of germanium from real fly ash leachates by ion-exchange extraction [J]. Minerals Engineering, 2011, 24: 35-41.

[8] HERNANDEZ-EXPOSITO A, CHIMENOS J, FERNANDEZ A, FONT O, QUEROL X, COCA P, PENA F G. Ion flotation of germanium from fly ash aqueous leachates [J]. Chemical Engineering Journal, 2006, 118: 69-75.

[9] CUI W, WANG S, PENG J, ZHANG L, ZHANG G. Catechol- functionalized nanosilica for adsorption of germanium ions from aqueous media [J]. Journal of Sol-Gel Science and Technology, 2016, 77: 666-674.

[10] LIANG D, WANG J, WANG Y. Germanium recovery by co-precipitation of germanium and iron in conventional zinc metallurgy [J]. Journal of the Southern African Institute of Mining and Metallurgy, 2008, 108: 715-718.

[11] KISLIK V S. Liquid membrane separation [M]. 1nd ed. Berlin: Springer, 2015.

[12] RAJA SULAIMAN R N, OTHMAN N, MOHAMED NOAH N F, JUSOH N. Removal of nickel from industrial effluent using a synergistic mixtures of acidic and solvating carriers in palm oil-based diluent via supported liquid membrane process [J]. Chemical Engineering Research and Design, 2018, 137: 360-375.

[13] HARRUDDIN N, OTHMAN N, LIM EE SIN A, RAJA SULAIMAN R N. Selective removal and recovery of Black B reactive dye from simulated textile wastewater using the supported liquid membrane process [J]. Environmental Technology, 2015, 36: 271-280.

[14] ZAHERI P, ABOLGHASEMI H, GHANNADI MARAGHE M, MOHAMMADI T. Intensification of Europium extraction through a supported liquid membrane using mixture of D2EHPA and Cyanex272 as carrier [J]. Chemical Engineering and Processing: Process Intensification, 2015, 92: 18-24.

[15] YANG X J, DUAN H P, SHI D Q, YANG R S, WANG S X, GUO H. Facilitated transport of phenol through supported liquid membrane containing bis(2-ethylhexyl) sulfoxide (BESO) as the carrier [J]. Chemical Engineering and Processing: Process Intensification, 2015, 93: 79-86.

[16] MAHDAVI H R, ARZANI M, PEYDAYESH M, MOHAMMADI T. Pertraction of l-lysine by supported liquid membrane using D2EHPA/M2EHPA [J]. Chemical Engineering and Processing: Process Intensification, 2016, 106: 50-58.

[17] KANDWAL P, DIXIT S, MUKHOPADHYAY S, MOHAPATRA P K, MANCHANDA V K. Mathematical modeling of Cs(I) transport through flat sheet supported liquid membrane using calix-[4]- bis(2,3-naptho)-18-crown-6 as the mobile carrier [J]. Desalination, 2011, 278: 405-411.

[18] LEOPOLD A A, COLL M T, FORTUNY A, RATHORE N S, SASTRE A M. Mathematical modeling of cadmium(II) solvent extraction from neutral and acidic chloride media using Cyanex 923 extractant as a metal carrier [J]. Journal of Hazardous Materials, 2010, 182: 903-911.

[19] DURAND-VIDAL S, SIMONIN J-P, TURQ P. Electrolytes at interfaces [M]. 1nd ed. Netherlands: Springer Science & Business Media, 2002.

[20] YANG Q, KOCHERGINSKY N M. Copper removal from ammoniacal wastewater through a hollow fiber supported liquid membrane system: Modeling and experimental verification [J]. Journal of Membrance Science, 2007, 297: 121-129.

[21] ALONSO M, LOPEZ-DELGADO A, SASTRE A M, ALGUACIL F J. Kinetic modelling of the facilitated transport of cadmium (II) using Cyanex 923 as ionophore [J]. Chemical Engineering Journal, 2006, 118: 213-219.

[22] ALGUACIL F J, ALONSO M. Chromium (VI) removal through facilitated transport using CYANEX 923 as carrier and reducing stripping with hydrazine sulfate [J]. Environmental Science & Technology, 2003, 37: 1043-1047.

[23] ALGUACIL F J, MARTINEZ S. Permeation of iron(III) by an immobilised liquid membrane using Cyanex 923 as mobile carrier [J]. Journal of Membrance Science, 2000, 176: 249-255.

[24] ALGUACIL F J, COEDO A G, DORADO M T, PADILLA I. Phosphine oxide mediate transport: modelling of mass transfer in supported liquid membrane transport of gold (III) using Cyanex 923 [J]. Chemical Engineering Science, 2001, 56: 3115-3122.

[25] SASTRE A, MADI A, CORTINA J, MIRALLES N. Modelling of mass transfer in facilitated supported liquid membrane transport of gold (III) using phospholene derivatives as carriers [J]. Journal of Membrance Science, 1998, 139: 57-65.

[26] SINGH S K, MISRA S, TRIPATHI S, SINGH D. Studies on permeation of uranium (VI) from phosphoric acid medium through supported liquid membrane comprising a binary mixture of PC88A and Cyanex 923 in n-dodecane as carrier [J]. Desalination, 2010, 250: 19-25.

[27] KAMRAN HAGHIGHI H, IRANNAJAD M, MORADKHANI D. Permeation and modeling studies on Ge(IV) facilitated transport using trioctylamine through supported liquid membrane [J]. Korean Journal of Chemical Engineering, 2018, 35: 53-60.

[28] KAMRAN HAGHIGHI H, IRANNAJAD M, FORTUNY A, SASTRE A M. Non-dispersive selective extraction of germanium from fly ash leachates using membrane-based processes [J]. Separation Science and Technology, 2019: 1-16.

[29] ADNAN S, HOANG M, WANG H, XIE Z. Commercial PTFE membranes for membrane distillation application: effect of microstructure and support material [J]. Desalination, 2012, 284: 297-308.

[30] ALGUACIL F J, COEDO A G, DORADO M T. Transport of chromium (VI) through a Cyanex 923–xylene flat-sheet supported liquid membrane [J]. Hydrometallurgy, 2000, 57: 51-56.

[31] KAMRAN HAGHIGHI H, IRANNAJAD M, FORTUNY A, SASTRE A M. Mathematical modeling for facilitated transport of Ge (IV) through supported liquid membrane containing Alamine 336 [J]. Chemical Papers, 2018, 72: 955-970.

[32] NAGY E, Basic equations of mass transport through a membrane layer [B]. 1nd ed. London: Elsevier, 2018.

[33] KOLEV S D, ST JOHN A M, CATTRALL R W. Mathematical modeling of the extraction of uranium(VI) into a polymer inclusion membrane composed of PVC and di-(2-ethylhexyl) phosphoric acid [J]. Journal of Membrane Science, 2013, 425-426: 169-175.

[34] HISS T G, CUSSLER E. Diffusion in high viscosity liquids [J]. AIChE Journal, 1973, 19: 698-703.

[35] PRASAD R, SIRKAR K. Dispersion‐free solvent extraction with microporous hollow‐fiber modules [J]. AIChE Journal, 1988, 34: 177-188.

[36] HISS T G, CUSSLER E L. Diffusion in high viscosity liquids [J]. AIChE Journal, 1973, 19: 698-703.

[37] ARSLAN G, TOR A, MUSLU H, OZMEN M, AKIN I, CENGELOGLU Y, ERSOZ M. Facilitated transport of Cr(VI) through a novel activated composite membrane containing Cyanex 923 as a carrier [J]. Journal of Membrane Science, 2009, 337: 224-231.

[38] NAVARRO R, SAUCEDO I, NUNEZ A, AVILA M, GUIBAL E. Cadmium extraction from hydrochloric acid solutions using Amberlite XAD-7 impregnated with Cyanex 921 (tri-octyl phosphine oxide) [J]. Reactive and Functional Polymers, 2008, 68: 557-571.

[39] JUMBRI K, ROZY M F A H, ASHARI S E, MOHAMAD R, BASRI M, MASOUMI H R F. Optimisation and characterisation of lipase-catalysed synthesis of a kojic monooleate ester in a solvent-free system by response surface methodology [J]. PloS One, 2015, 10: e0144664.

[40] HAMZAOUI A H, JAMOUSSI B, M'NIF A. Lithium recovery from highly concentrated solutions: Response surface methodology (RSM) process parameters optimization [J]. Hydrometallurgy, 2008, 90: 1-7.

Cyanex 923支撑液膜中锗的迁移：数学建模

Hossein KAMRAN HAGHIGHI¹, Mehdi IRANNAJAD¹, Ana MARIA SASTRE²

1. Department of Mining and Metallurgical Engineering, Amirkabir University of Technology, Tehran, Iran;

2. Department of Chemical Engineering, Universitat Politecnica de Catalunya, ESTEIB, Av. Diagonal 647, 08028 Barcelona, Spain

摘 要：建立一个数学模型，用于监测草酸溶液中锗(IV)穿过含有4种三烷基氧化膦(Cyanex 923)的平板支撑液膜(FSSLM)的促进迁移过程。FSSLM建模是基于由液-液萃取(LLX)模型计算得出的萃取常数(K_ext)。LLX模型提供一种可靠的萃取常数计算方法(K_ex=2.057×10³ L/mol⁴)。根据萃取常数、Fick定律和扩散原理，利用Matlab软件对FSSLM模型进行求解。该模型预测的总传质系数(K_org)为3.84 cm/s。利用该总传质系数，得出Cyanex 923浓度为0.126、0.252、0.378、0.505、0.631和0.757 mol/L时的扩散系数(D_m)分别为8.50×10^-4、4.30×10^-4、1.87×10^-4、5.87×10^-5、2.57×10^-5和2.09×10^-5 cm²/s。结果表明，本研究得出的扩散速率大于大多数类似的FSSLM体系的扩散速率。这些FSSLM体系都含有Cyanex 923，用于迁移各种金属。模型值与实验数据吻合良好，表明该数学模型具有良好的可靠性。

关键词：支撑液膜；Cyanex 923；锗；迁移；数学建模

(Edited by Xiang-qun LI)

Corresponding author: Mehdi IRANNAJAD; E-mail: iranajad@aut.ac.ir

DOI: 10.1016/S1003-6326(19)65103-4