Electro-flotation and collision-attachment mechanism of fine cassiterite
来源期刊:中国有色金属学报(英文版)2012年第4期
论文作者:覃文庆 任浏祎 王佩佩 杨聪仁 张雁生
文章页码:917 - 924
关键词:锡石;颗粒气泡相互作用;细粒浮选;电解浮选;碰撞-粘附几率
Key words:cassiterite; particle-bubble interaction; fine particle flotation; electro-flotation; collision-attachment probability
摘 要:为了研究细粒锡石电解浮选中颗粒气泡间的相互作用,分析不同粒级锡石的浮选回收率和锡石颗粒与氢气泡的碰撞机理。浮选实验在一个单泡电解浮选装置中进行,实验结果表明,<10 μm, 10~20 μm, 20~38 μm和38~74 μm粒级的锡石分别与50~150 μm, 约250 μm,约74 μm和约74 μm尺寸的气泡相匹配,可以获得较好的浮选回收率。因此,颗粒和气泡的大小直接影响锡石的浮选回收率。利用碰撞、粘附和捕集模型进行碰撞、粘附、分离和捕集几率的计算。理论计算结果发现碰撞几率随着颗粒尺寸的减小以及气泡尺寸(<150 μm)的增大而显著降低。有效的碰撞有利于粘附几率的增加,从而有利于提高浮选回收率。
Abstract:
In order to discuss the particle-bubble interaction during the electro-flotation of cassiterite, the recovery of cassiterite with different particle sizes was investigated, and the collision mechanism between the cassiterite particles and H2 bubbles was explored. The flotation tests were carried out in a single bubble flotation cell. The results show that cassiterite particles <10 μm, 10-20 μm, 20-38 μm and 38-74 μm match with bubbles with size of 50-150 μm, about 250 μm, 74 μm and 74 μm, respectively, and a better recovery can be obtained. It is demonstrated that the recovery of cassiterite is influenced by the size of cassiterite particles and bubbles. Furthermore, the probabilities of collision, adhesion, detachment and collection were calculated using the collision, attachment and collection models. Theoretical calculation results show that the collision probability decreases sharply with decreasing particle size and increasing bubble size (below 150 μm). The attachment probability would increase from the effective collision, leading to the increase of recovery.

![]()

Trans. Nonferrous Met. Soc. China 22(2012) 917-924
QIN Wen-qing, REN Liu-yi, WANG Pei-pei, YANG Cong-ren, ZHANG Yan-sheng
School of Minerals Processing and Bioengineering, Central South University, Changsha 410083, China
Received 13 April 2011; accepted 30 August 2011
Abstract: In order to discuss the particle-bubble interaction during the electro-flotation of cassiterite, the recovery of cassiterite with different particle sizes was investigated, and the collision mechanism between the cassiterite particles and H2 bubbles was explored. The flotation tests were carried out in a single bubble flotation cell. The results show that cassiterite particles <10 μm, 10-20 μm, 20-38 μm and 38-74 μm match with bubbles with size of 50-150 μm, about 250 μm, 74 μm and 74 μm, respectively, and a better recovery can be obtained. It is demonstrated that the recovery of cassiterite is influenced by the size of cassiterite particles and bubbles. Furthermore, the probabilities of collision, adhesion, detachment and collection were calculated using the collision, attachment and collection models. Theoretical calculation results show that the collision probability decreases sharply with decreasing particle size and increasing bubble size (below 150 μm). The attachment probability would increase from the effective collision, leading to the increase of recovery.
Key words: cassiterite; particle-bubble interaction; fine particle flotation; electro-flotation; collision-attachment probability
1 Introduction
The flotation of fine particles has become particularly important in recent years as advances have been made in grinding, which allows low grade mineral deposits to be economically exploited[1,2]. The poor recovery of fine minerals by flotation can be attributed to the low probability of bubble-particle collision, which decreases with the decrease of particle size [3]. Particle collection by air bubbles is regarded as the heart of froth flotation operation. Flotation performance depends on several key factors, such as particle size and surface chemistry. It is necessary to research fine particle flotation due to the complexity of some ore bodies [4]. Therefore, fine particle flotation has gained significant attention over the last decade.
Particle-bubble interaction is the fundamental process in flotation determined by the physics of the particle and bubble motions and the hydrodynamics of liquid flow [5], and it has been studied most extensively [6-8]. Study of interactions between solid particles and air bubbles in aqueous solutions is a key to understand the froth flotation [9,10]. Many attentions have been focused on the understanding and controlling of the interactions between colliding particles and bubbles. However, the principles governing the interactions are not fully understood. Flotation is now considered to contain three sub-processes, including the collision between air bubbles and particles, the attachment and detachment of the particles and bubbles [11-14]. The bubble-particle collision has been studied most extensively [7,8,15,16]. Collision is governed by the fluid mechanics of the particles in the long-range hydrodynamic force field around the bubble, and there are various parameters impacting the bubble-particle collision probability including particle size and density, bubble size, bubble rising velocity and bubble surface mobility. The increase of bubble-particle collision probability with the increase of particle size and decrease of bubble size is predicted by the collision models [17], which is in agreement with the bubble-particle collision experiments [16,18-20]. It has been found that the bubble-particle collision probability increases with the decrease of bubble size [21-23]. The detachment process is governed by the capillary force, the particle mass and the detaching forces due to the turbulent acceleration. The factors influencing bubble-particle attachment can be analyzed from both thermodynamic and kinetic points of view [17,24]. The increase in particle surface hydrophobicity is beneficial to bubble-particle attachment. It has been reported that the experimental flotation rates and recoveries increase with increasing electrolyte concentration [25-28]. The positive effect of electrolyte concentration on the flotation rates and recoveries is mainly attributed to the increase in bubble-particle attachment probability [29]. In addition to the kinetics and thermodynamics influences of electrolyte concentration on the bubble- particle attachment probability, another possible reason is that gas solubility decreases as the electrolyte concentration increases [30]. This results in the precipitation of gas molecules as nanobubbles on the particle surface, which is advantageous for bubble-particle attachment [10,31].
It is important to note that the processes of bubble-particle collision, attachment and detachment are not completely discrete. Since the governing (long-range hydrodynamic, surface and capillary) forces are independent, each of them has significant influence on the processes. Consequently, the collision, attachment and detachment can be analyzed independently. This distinction simplifies the modeling of each process [32].
The purpose of this study is to demonstrate the relationship between the recovery and sizes of the particle and bubble. The electro-flotation experiments of fine cassiterite particles are conducted. Furthermore, the results are analyzed using the models of collision and attachment to calculate the collision and attachment probability.
2 Experimental
2.1 Material
High-grade cassiterite concentrate was obtained by gravity separation of a tin ore from Gaofeng Mining Co.,Ltd. in Guangxi, China. The concentrate was further purified by removing traces of magnetic impurities using magnetic separator, CaCO3 by adding dilute hydrochloric acid solution and stirring for about a week, and SiO2 by using shaking table. The X-ray diffraction result is shown in Fig. 1. No peaks of impurities are detected, which indicates that SnO2 is successfully obtained with high purity. Chemical analysis of the concentrate sample shows that the purity of SnO2 is 94%, which is deemed sufficiently pure for research purposes. Finally, the samples with particle size <10 μm, 10-20 μm, 20-38 μm and 38-74 μm were prepared by hydraulic classification.
Chemical pure grade sodium oleate from Sinopharm Chemical Reagent Co., Ltd. was used as a collector. Other chemicals employed in the test were of analytical reagent grade. All the experiments were carried out with distilled water.
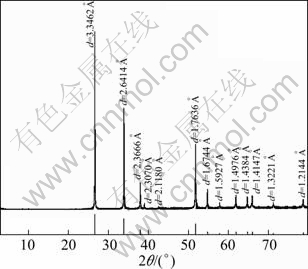
Fig. 1 XRD pattern of purified samples
A single bubble flotation tube was modified from a Hallimond tube. The H2 bubbles produced from cathode were used for carrying fine cassiterite particles. The O2 bubbles produced from anode were separated by PTFE diaphragm and exported from latex tube connected to the above anode. The bubble size was controlled by a stainless steel wire mesh. Another single bubble electro-flotation tube, the side of which was square, was used to observe the bubble size and interaction between the fine cassiterite particles and H2 bubbles.
2.2 Electro-flotation
Electro-flotation tests were conducted in the modified Hallimond tube in 1% Na2SO4 electrolyte solution, while the pulp density was 1%. The mineral sample was mixed with the collector reagent for 5 min using magnetic stirrer at stirring rate of 1000 r/min, followed by flotation for 8 min by H2 bubbles with different sizes. In each test, mineral sample of 1 g was dispersed using ultrasonic wave with 90 mL Na2SO4 solution as the medium. The collector, sodium oleate, was added into the pulp at pH 7.0 and mixed for 5 min. The pH value of pulp was adjusted with 1% NaOH and 1% H2SO4, and then the pulp was transferred into an electro-flotation tube with a peristaltic magnetic stirrer, the electro-flotation tube was fixed and connected to the power. DC power supply was turned on and the current was regulated, and then electrified for 1 min. The H2 bubbles were introduced into the electro-flotation for further 1 min, so the cassiterite particles were carried out from the pulp during the flotation for 8 min, which were the product of the electro-flotation. Then the particles were filtered, dried, weighed and analyzed. Unless otherwise mentioned, the pH values stated were obtained before the electro-flotation test.
2.3 Electrolysis principle
Figure 2 shows the electrolysis unit. It is seen that the flake graphite and stainless steel wire meshes are used as the anode and cathode, respectively. The negatively charged oxygen ions obtain electrons and release oxygen at the anode, while the positively charged hydrogen ions lose electrons and release hydrogen at the cathode. The electrolysis equations can be represented as:
Anode: 2O2--4e=O2↑
Cathode: 4H++4e=2H2↑
where the amount of O2 or H2 can be controlled by the current depending on the applied voltage. The relation between the amount of O2 or H2 and current can be expressed as:
q=(Mr/nF)It
where q is the amount of substance of H2 produced in the process of electrolysis; Mr is atomic relative mass; I is current; t is time; n is number of electrons obtained or lost in the process of electrolysis, and F is Faraday constant, the value of which is 96500 C/mol. It is observed that the amount of substance of H2 is in direct proportion to current.
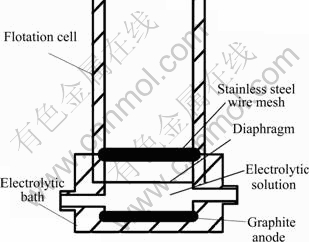
Fig. 2 Schematic diagram of electrolysis
3 Results and discussion
3.1 Electro-flotation of cassiterite
3.1.1 Influence of sodium oleate concentration on recovery of cassiterite
The electro-flotation of cassiterite was conducted using the modified Hallimond tube with sodium oleate concentrations of 0, 2, 5, 10, 20, 30, 40 and 50 mg/L at pH=8 and pulp density of 1%, respectively. The results are shown in Fig. 3.
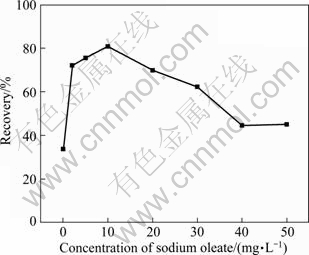
Fig. 3 Recovery of SnO2 with particle size <10 μm as function of sodium oleate concentration at pH=8.0
The best recovery is obtained in the presence of sodium oleate with concentration of 10 mg/L. The recovery of cassiterite increases and decreases with the increase of the concentration of sodium oleate below and above 10 mg/L, respectively. It is observed that the size of oil agglomerate decreases and the conversion time becomes longer with increasing sodium oleate dosage above 10 mg/L in experiments.
3.1.2 Influence of pH on recovery of cassiterite
The recovery of cassiterite is obtained at pH values of 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0 and 10.0 during the cassiterite flotation experiments conducted at sodium oleate concentration of 10 mg/L, pH=8 and pulp density of 1%. The results are shown in Fig. 4.

Fig. 4 Recovery of SnO2 as function of pH under condition of 10 mg/L sodium oleate, pH=8 and pulp density of 1%
It is shown that the recovery of cassiterite increases slightly with the increase of pH from 3 to 8. A better flotation response can be obtained in alkaline pulp, especially at pH=8.0. So, it is demonstrated that the optimum pH value for the electro-flotation of cassiterite is 8.0.
3.1.3 Influence of current and bubble size on recovery of cassiterite
Figure 5 illustrates the effect of current on the recovery of cassiterite with particle size <10 μm as a function of bubble size under condition of pH=8.0, pulp density of 1% and sodium oleate concentration of 10 mg/L.
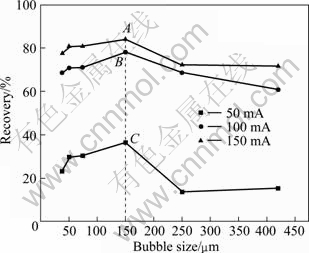
Fig. 5 Relationship between recovery and bubble size at different currents in the presence of collector
It is observed that the recovery of cassiterite increases slightly with increasing bubble size from 50 to 150 μm; however, it decreases sharply with the bubble size increasing above 150 μm. The highest recovery could be obtained at the bubble size of 150 μm. In addition, the bubbles with size of 50-150 μm are beneficial to carry the cassiterite particles out <10 μm out. Therefore, it could be concluded that there is a matching degree for the fixed size of cassiterite. According to the method introduced by GRAU and HEISKANEN [33] and YANG et al [34], the H2 bubble size is observed close to the corresponding cathode aperture.
The flotation responses of cassiterite with sodium oleate depend on the matching degree between particle size and bubble size. The results indicate that good floatability of cassiterite <10 μm occurs when the bubble size is 50-150 μm. It is also demonstrated that the recovery of cassiterite increases with the increase of current, 3 curves at different currents of 50, 100, and 150 mA in Fig. 5 demonstrate it. When the bubble size is fixed, the recovery reaches the highest at 150 mA and lowest at 50 mA. There is only a slight increase in the recovery of cassiterite at 100 mA compared with that at 150 mA, so 100 mA is chosen in the following tests. The quantity of H2 bubbles is directly proportional to current, and the H2 bubbles quantity at points A, B and C in Fig. 5 calculated by a series of equations are 1.51×107, 1.01×107 and 5.03×106.
3.1.4 Influence of particle size and bubble size on flotation recovery
Figure 6 illustrates the effect of 4 fractions of cassiterite with different sizes on the recovery as a function of bubble size under the conditions of pH=8.0, pulp density of 1% and sodium oleate of 10 mg/L.
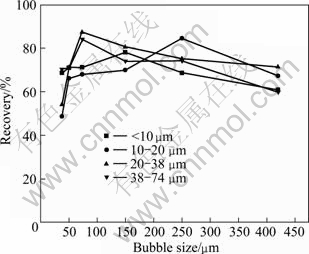
Fig. 6 Effect of bubble size and cassiterite size on flotation recovery at current of 100 mA, pH=8 and pulp density of 1% in the presence of 10 mg/L sodium oleate
It can be seen that there is matching bubble size for the cassiterite particles size. The matching bubble sizes of <10 μm, 10-20 μm, 20-38 μm and 38-74 μm cassiterite particles are 50-150 μm, 250 μm, 74 μm and 74 μm, respectively. Each particle fraction of cassiterite corresponds to a certain range of bubble size, in which the highest recovery can be achieved. An interesting result is obtained compared to the findings of previous study that the cassiterite with particle size of 20-38 μm and 38-74 μm should match with bubbles with size of about 250 μm or bigger. Two reasons may be responsible for this incoherence. First, this particular size fraction was obtained using a homemade centrifugal sedimentation device, which have produced a sample with a wider size distribution than those produced by screening. Second, different collectors were used. Anyway, the advantages of controlling bubble size to improve the recovery of fine particles are demonstrated in this study.
3.2 Collision mechanism between fine cassiterite and bubble
3.2.1 Probability of collision as functions of particle and bubble size
Collision between particles and bubbles is an important step in the flotation process. The collision mechanism can be explored by calculating collision probability using an empirical equation as: [35]
![]() (1)
(1)
The pulp is an intermediate flow, in which Bc is a function of the Reynolds number of the bubble and n=2 for the bubbles used in flotation, Bc and n can be described as:
![]() (2)
(2)
Substituting Eq. (2) into Eq. (1), it is obtained that
![]() (3)
(3)
where
![]() (4)
(4)
where Pc is the probability of particle-bubble collision; dp is the particle size of cassiterite; db is the bubble size; Re is the Reynolds number; vb is the rising velocity of bubbles; ρf is the fluid density; η is the fluid viscosity. The parameters of Re, ρf and η are constants, and vb can be measured through experiments. However, variables dp and db are unknown. db is given a fixed value, the fitted curve illustrating the relation of particle size and collision probability is created by Eq. (1), and the result is shown in Fig. 7.
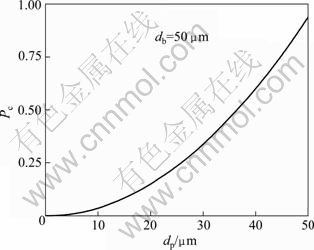
Fig. 7 Variation of collision probability as function of particle size
Figure 7 interprets the effect of particle size on the collision probability with a certain bubble size. The collision probability decreases sharply with the decrease of particle size. It can be concluded that the attachment probability would increase from the effective collision, leading to the increase of the recovery of cassiterite, which corresponds with the previous experimental results.
The relationship between the bubble size and the collision probability is determined by the fitted curve as shown in Fig. 8, which is also described by Eq. (1) when the value of particle size dp is fixed at 5 μm. The results show that the probability of particle-bubble collision decreases with the increase of bubble size. It is concluded that smaller bubbles result in higher collection efficiency with a given particle size. However, the collision probability could not be affected by the bubbles with the size above 150 μm. SCHULZE [14] kept the view that the probability of particle-bubble collision is influenced not only by dp and db, but also by the critical thickness of rupture of the liquid film on mineral surface. Moreover, the motion of particles approaching a bubble surface is influenced by a number of parameters, including the mass of the particle (inertial effect), the weight of the particle (gravitational effect) and the liquid flow passing the bubble (interceptional effect). The effect of each parameter is modeled independently by employing an equation [7]. The overall collisions between the particles and bubbles consist of the inertial, gravitational and interceptional collisions. However, it is the ideal way to research the collision process. In fact, the collision probability is also controlled by other parameters [7,12]. For example, the mobility of the bubble surface should be included in the analysis [15]. In this study, only the particle size and bubble size are considered important parameters affecting the probability of particle-bubble collision.

Fig. 8 Variation of collision probability as function of bubble size
3.2.2 Probability of particle-bubble adhesion
The equation for calculating the probability of particle-bubble attachment given by LUTTRELL and YOON [35] is shown as:
![]() (5)
(5)
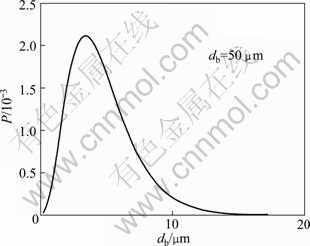
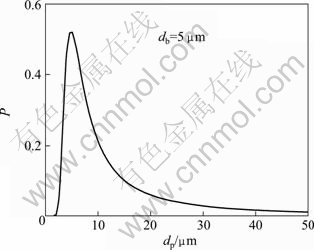
where Pa is the probability of adhesion; ti is the contact time, the time of particle motion in the proximity of the bubble, which can be defined by experiment; vb is the rising velocity of bubbles; 0 The fitted curves of Eq. (5) with db=50 μm and dp=5 μm is shown in Figs. 9 and 10, respectively. Fig. 9 Variation of attachment probability as function of particle size Fig. 10 Variation of attachment probability as function of bubble size Figures 9 and 10 indicate the relationships between attachment probability and particle size and bubble size, respectively. The probability of particle-bubble attachment is a function of the contact and attachment time according to Eq. (5). After colliding with a bubble, the particle deforms the bubble surface and then slides along the surface until it reaches the maximum collision angle. Figure 9 shows that the value of Pa decreases with increasing value of dp when the values of dp and ti are determined. It is indicated that the smaller the particle size is, the greater the probability of attachment to bubbles becomes. Therefore, the attachment would undoubtedly occur once the fine particles collide with the bubble surface. Hence, the attachment of bubbles and fine particles, as well as the floatability of fine particles depend on the collision probability of fine particles and bubbles. The low collision probability between fine particles and bubbles is the dominant factor for the flotation of fine particles. It is clear that the attachment probability between particle and bubble increases with the decrease of bubble size according to the fitting curve shown in Fig. 10, which is consistent with the results obtained from previous research. 3.2.3 Detachment probability between particles and bubbles Fine particles could be detached from the bubbles in turbulent flow force field. Bubble-particle aggregate stability is determined by the adhesive force acting on the attached particle, and it is the key issue to prevent the particle from detaching from the bubble surface under the dynamic forces existing in flotation cells. The detachment probability between particles and bubbles is related to many factors such as the particle weight, turbulent inertial forces, bubble size and the maximum size of floatable particles. This study focuses on the analysis of interaction between fine particles and bubbles. It was reported that the detachment probability decreases with the decease of the particle size in previous research. WOODBURN et al [36] gave the equation for calculating detachment probability as: where Pd is the detachment probability and dmax is the maximal particle size attached to bubble. Pd increases with the increase of particle size because of the increased detachment force, but it may be neglected for very small particles. For example, the detachment hardly happens for the particles with size of 1 μm. Hence, the detachment probability is not considered here. 3.2.4 Probability of collection as functions of particle size and bubble size The probability of collection (P) is calculated as [35]: Substitute Eqs. (3), (5) and (6) into Eq. (7), a new function dominated by only two variables dp and db is obtained. The new fitted curves according to the new function are shown in Figs. 11 and 12 for fixed values of db and dp, respectively. Figure 11 describes the variation of collection probability P with particle size and fixed bubble size. It can be obviously seen that there is a peak value of P, which indicates that the maximal collection can be probably obtained within a certain range of particle size when the bubble size is fixed. The result shows that the fitted model coincides well with the experimental data of electro-flotation. The fitted curve of equation for the fixed value of dp is shown in Fig. 12. It is observed that the variation of collection probability with bubble size is similar to that with particle size. Consequently, it is demonstrated that the maximal probability could be obtained at the optimum matching of particle and bubbles size. Fig. 11 Variation of collection probability as function of particle size Fig. 12 Variation of collection probability as function of bubble size 4 Conclusions 1) The optimum conditions for the electroflotation of cassiterite are that the dosage of sodium oleate as a collector is 10 mg/L, the pH value of pulp is 8.0 and the current is 100 mA. There is a matching range between the different particle sizes and bubble sizes, in which the best recovery can be obtained. The cassiterite particles with size <10 μm match bubbles with size of 50-150 μm, cassiterite particles with size of 20-10 μm match bubbles with size of about 250 μm, while cassiterite particles with size of 20-38 μm and 38-74 μm match bubbles with size of about 74 μm. 2) Theoretical calculation of collision and attachment probability shows the collision and adhesion mechanism of fine cassiterite flotation. The particle-bubble interaction is affected by the bubble size and particle size, which influences not only the collision probability and attachment probability of particles and bubbles sharply, but also the collection probability of particle-bubble finally. These are in agreement with the experimental data for electro-flotation recovery of cassiterite. References [1] GEORGE P, NGUYEN A V, JAMESON G J. Assessment of true flotation and entrainment in the flotation of submicron particles by fine bubbles [J]. Minerals Engineering, 2004, 17(7-8): 847-853. [2] WATERS K E, HADLER K, CILLIERS J J. The flotation of fine particles using charged microbubbles [J]. Minerals Engineering, 2008, 21(12-14): 918-923. [3] YOON R H. The role of hydrodynamic and surface forces in bubble-particle interaction [J]. International Journal of Mineral Processing, 2000, 58(1-4): 129-143. [4] CILEK E C, UMUCU Y. A statistical model for gangue entrainment into froths in flotation of sulphide ores [J]. Minerals Engineering, 2001, 14(9): 1055-1066. [5] NGUYEN A V, EVANS G M. Attachment interaction between air bubbles and particles in froth flotation [J]. Experimental Thermal and Fluid Science, 2004, 28(5): 381-385. [6] JAMESON G J, NAM S, YOUNG M M. Physical factors affecting recovery rates in flotation [J]. Minerals Science and Engineering, 1977, 9(3): 103-118. [7] SCHULZE H J. Hydrodynamics of bubble-mineral particle collisions [J]. International Journal of Mineral Processing, 1989, 5(1-4): 43-76. [8] NGUYEN A V. Hydrodynamics of liquid flows around air bubbles in flotation: a review [J]. International Journal of Mineral Processing, 1999, 56(1-4): 165-205. [9] NGUYEN A V, NALASKOWSKI J, MILLER J D. A study of bubble-particle interaction using atomic force microscopy [J]. Minerals Engineering, 2003, 16(11): 1173-1181. [10] KRALCHEVSKY P A, BONEVA M P, DANOV K D, CHRISTOV N C. Attraction between particles at a liquid interface due to the interplay of gravity- and electric-field-induced interfacial deformations [J]. Langmuir, 2009, 25(16): 9129-9139. [11] FINCH J A, DOBBY G S, Columnflotation: A selected review [J]. International Journal of Mineral Processing, 1990, 33(1-4): 343-354. [12] RALSTON J, FORNASIERO D, HAYES R. Bubble-particle attachment and detachment in flotation [J]. International Journal of Mineral Processing, 1999, 56(1-4): 133-164. [13] KING R P. Modeling and simulation of mineral processing systems [M]. Boston: Butterworth Heinemann, 2001: 403. [14] SCHULZE H J. Physico-chemical elementary process in flotation [J]. Amsterdam: Elsevier, 1984: 348. [15] DAI Z F, FORNASIERO D, RALSTON J. Particle-bubble collision models—A review [J]. Advances in Colloid and Interface Science, 2000, 85(2-3): 231-256. [16] YOON R H, LUTTRELL G H. The effect of bubble size on fine particle flotation [J]. Miner Proc Extract Met Rev, 1989, 5(1-4): 101-122. [17] MIETTINEN T, RALSTON J, FORNASIERO D. The limits of fine particle flotation [J]. Minerals Engineering, 2010, 23(5): 420-437. [18] ANFRUNS J F, KITCHENER J A. Rate of capture of small particles in flotation [J]. Transactions of the Institution of Mining and Metallurgy, Section C: Mineral Processing and Extractive Metallurgy, 1977, 86(5): 9-15. [19] HEWITT D, FORNASIERO D, RALSTON J. Bubble-particle attachment [J]. Journal of the Chemical Society, Faraday Transactions, 1995, 91(13): 1997-2001. [20] DAI Z, DUKHIN S S, FORNASIERO D, RALSTON J. The inertial hydrodynamic interaction of particles and rising bubbles with mobile surfaces [J]. Journal of Colloid and Interface Science, 1998, 197(2): 275-292. [21] REAY D, RATCLIFF G A. Removal of fine particles from water by dispersed air flotation [J]. Canadian Journal of Chemical Engineering, 1973, 51(2): 178-185. [22] YANG S M, HAN S P, HONG J J. Capture of small particles on a bubble collector by brownian diffusion and interception [J]. Journal of Colloid and Interface Science, 1995, 169(1): 125-134. [23] NGUYEN A V, GEORGE P, JAMESON G J. Demonstration of a minimum in the recovery of nanoparticles by flotation: Theory and experiment [J]. Chemical Engineering Science, 2006, 61(8): 2494-2509. [24] BEAUSSART A, PARKINSON L, MIERCZYNSKA-VASILEV A, RALSTON J, BEATTIE D A. Effect of adsorbed polymers on bubble-particle attachment [J]. Langmuir, 2009, 25(23): 13290-13294. [25] KLASSEN V I, MOKROUSOV V A. An introduction to the theory of flotation [M]. London: Butterworths, 1963: 102-123. [26] COLLINS G L, JAMESON G J. Double-layer effects in the flotation of fine particles [J]. Chemical Engineering Science, 1977, 32(3): 239-246. [27] CRAWFORD R, RALSTON J. The influence of particle size and contact angle in mineral flotation [J]. International Journal of Mineral Processing, 1988, 23 (1-2): 1-24. [28] DAI Z F, FORNASIERO D, RALSTON J. Particle-bubble attachment in mineral flotation [J]. Journal of Colloid and Interface Science, 1999, 217(1): 70-76. [29] PUSHKAROVA R A, HORN R G. Bubble-solid interactions in water and electrolyte solutions [J]. Langmuir, 2008, 24(16): 8726-8734. [30] WEISENBERGER S, SCHUMPE A. Estimation of gas solubilities in salt solutions at temperatures from 273 K to 363 K [J]. AIChE Journal, 1996, 42(1): 298-300. [31] DAI Z, FORNASIERO D, RALSTON J. Influence of dissolved gas on bubble-particle heterocoagulation [J]. Journal of the Chemical Society, Faraday Transactions, 1998, 94(14): 1983-1987. [32] PHAN C M, NGUYEN A V, MILLER J D, EVANS G M, JAMESON G J. Investigations of bubble-particle interactions [J]. International Journal of Mineral Processing, 2003, 72(1-4): 239-254. [33] GRAU R A, HEISKANEN K. Bubble size distribution in laboratory scale flotation cells [J]. Minerals Engineering, 2005, 18(12): 1164-1172. [34] YANG Chun-hua, XU Can-hui, MU Xue-min, ZHOU Kai-jun. Bubble size estimation using interfacial morphological information for mineral flotation process monitoring [J]. Transactions of Nonferrous Metals Society of China, 2009, 19(3): 694-699. [35] LUTTRELL G H, YOON R H. A hydrodynamic model for bubble-particle attachment [J]. Journal of Colloid and Interface Science, 1992, 154(1): 129-137. [36] WOODBURN E T, KING R P, COLBORN R P. The effect of panicle size distribution on the performance of a phosphate flotation process [J]. Metall Trans, 1971, 2(11): 3163-3174. 覃文庆,任浏祎,王佩佩,杨聪仁,张雁生 中南大学 资源加工与生物工程学院,长沙 410083 摘 要:为了研究细粒锡石电解浮选中颗粒气泡间的相互作用,分析不同粒级锡石的浮选回收率和锡石颗粒与氢气泡的碰撞机理。浮选实验在一个单泡电解浮选装置中进行,实验结果表明,<10 μm, 10~20 μm, 20~38 μm和38~74 μm粒级的锡石分别与50~150 μm, 约250 μm,约74 μm和约74 μm尺寸的气泡相匹配,可以获得较好的浮选回收率。因此,颗粒和气泡的大小直接影响锡石的浮选回收率。利用碰撞、粘附和捕集模型进行碰撞、粘附、分离和捕集几率的计算。理论计算结果发现碰撞几率随着颗粒尺寸的减小以及气泡尺寸(<150 μm)的增大而显著降低。有效的碰撞有利于粘附几率的增加,从而有利于提高浮选回收率。 关键词:锡石;颗粒气泡相互作用;细粒浮选;电解浮选;碰撞-粘附几率 (Edited by FANG Jing-hua) Foundation item: Project (50774094) supported by the National Natural Science Foundation of China; Project (2010CB630905) supported by the National Basic Research Program of China Corresponding author: QIN Wen-qing; Tel: +86-731-88830884; E-mail: qinwenqing1@126.com DOI: 10.1016/S1003-6326(11)61265-X

![]() (6)
(6)![]() (7)
(7)
细粒锡石的电解浮选及碰撞粘附机理

