J. Cent. South Univ. (2016) 23: 898-905
DOI: 10.1007/s11771-016-3137-6
Rheological properties of surrounding rock in deep hard rock tunnels and its reasonable support form
WANG Hui(王辉)1, 2, CHEN Wei-zhong(陈卫忠)2, 3, WANG Qing-biao(王清标)1, ZHENG Peng-qiang(郑朋强)1
1. Department of Resources and Civil Engineering, Shandong University of Science and Technology,
Tai’an 271019, China;
2. Geotechnical & Structural Engineering Research Center, Shandong University, Ji’nan 250061, China;
3. State Key Laboratory of Geomechanics and Geotechnical Engineering (Institute of Rock and Soil Mechanics, Chinese Academy of Sciences), Wuhan 430071, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: Second lining stability, which is the last protection in tunnel engineering, is critically important. The rheological properties of the surrounding rock heavily affect second lining stability. In this work, we used laboratory triaxial compressive rheological limestone tests to study nonlinear creep damage characteristics of surrounding rock mass in construction projects. We established a nonlinear creep damage constitutive model for the rock mass, as well as a constitutive model numerical implementation made by programming. Second, we introduced a new foam concrete with higher compression performance and good ductility and studied its mechanical properties through uniaxial and triaxial tests. This concrete was used as the filling material for the reserved deformation layer between the primary support and second lining. Finally, we proposed a high efficiency and accuracy staged optimization method. The minimum reserved deformation layer thickness was established as the optimization goal, and the presence of plastic strain in the second lining after 100 years of surrounding rock creep was used as an evaluation index. Reserved deformation layer thickness optimization analysis reveals no plastic strain in the second lining when the reserved deformation minimum thickness layer is 28.50 cm. The results show that the new foam concrete used as a reserved deformation layer filling material can absorb creep deformation of surrounding rock mass, reduce second lining deformation that leads to plastic strain, and ensure long-term second lining stability.
Key words: rheological test; constitutive model; staged optimization analysis; reasonable support form
1 Introduction
China has recently undergone economic construction development, such as the implementation of western development strategies. This has presented new opportunities for railway, highway, and hydraulic engineering. Complex topographic and geological conditions in western China have required a large number of bridge and tunnel projects. As a result, more tunnels pass through high geostress areas, which present challenges and opportunities for construction design. Generally, soft rocks have obvious rheological properties. However, engineering practices show that under high geostress, even hard rock masses such as quartzite, igneous rock, and limestone display soft rock rheological properties [1-5]. Unlike research for soft rock, research for hard rock construction is relatively underdeveloped [6].
Research shows that compared with ordinary tunnel construction, construction in high geostress regions leads to high second lining stress due to second lining force and deformation over time. The second lining serves as a safety reserve tunnel; its stress size and deformation are used to evaluate tunnel safety. So, improving second lining stress tolerance is important for increasing tunnel stability. A reserved deformation filling layer is applied between the first and second linings to absorb surrounding rock creep deformations, reduce second lining stress and deformation, and ensure long-term tunnel stability. So, the reserved deformation layer filling material must have high absorption deformation properties, and maintain strength and integrity after deformation.
This work explores a new method of providing a reasonable support form for tunnel construction in high geostress regions. First, we performed laboratory triaxial compressive rheological tests on surrounding rocks to research creep damage characteristics. Second, we proposed a new foam concrete filling material for the reserved deformation layer; we studied its deformation characteristics through uniaxial and triaxial tests. Finally, we used the proposed foam concrete as the filling material between the primary support and second linings. We measured the presence of plastic strain in the second lining after 100 years of surrounding rock creep as an evaluation index. The thickness of reserved deformation layer was optimized in stages to provide a new idea for tunnel support foam in high geostress regions.
2 Nonlinear creep damage model
In western China, the maximum depth of a tunnel to be constructed is 1360 m and most surrounding rock is hard limestone. Under low bearing stress, limestone creep deformation is very small and the deformation tends to stabilize after a short time. At high stress levels, steady-state creep appears after obvious initial creep and then the deformation tends to stabilize. When the stress level reaches a critical value, rock creep accelerates at each stage, resulting in structure failure. Limestone is very strong, so in general engineering calculations, the creep process of limestone includes the initial creep and stable creep stage, and the possibility of entering into the acceleration creep stage is very small.
2.1 Experimental study on limestone creep characteristics
Creep tests for rock specimens were carried out with a TLW-2000 triaxial rheological testing machine at a high pressure confinement (Fig. 1). Its maximum confining pressure was 70 MPa, and its axial load could reach 2000 kN. Axial and circumferential deformationcould be collected automatically, and the minimum measurable deformation was 1×10-3mm.

Fig. 1 TLW-2000 triaxial rheological testing machine with a high pressure confinement
According to the buried engineering rock mass depth and the in-situ ground stress results, we carried out a triaxial creep test on limestone under a 30 MPa confining pressure. Figure 2 shows the creep test results; the corresponding number on the curve indicates deviatoric stress during the test period. From Fig. 2, it can be found that during the step loading process when the deviatoric stress is less than 80 MPa, after the initial creep, creep deformation tends to gradually stabilize. Therefore, the triaxial creep test proved that limestone displayed hard rock creep properties.
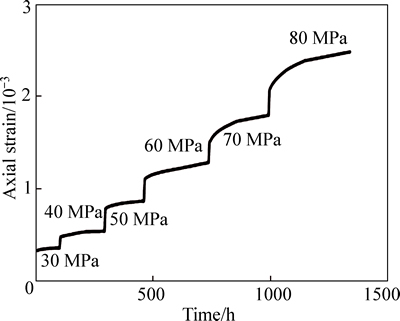
Fig. 2 Creep test curve under a 30 MPa confining pressure
2.2 Nonlinear creep damage constitutive model
The relationship of creep strain, deviatoric stress, and the time for hard rheological rock masses can be expressed as follows:
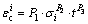 (1)
(1)
where P1, P2 and P3 are test parameters,  is the creep strain, σi is the deviatoric stress in the i direction, and t is time.
is the creep strain, σi is the deviatoric stress in the i direction, and t is time.
In practical geotechnical engineering, the strength, rheological properties, and internal damage mechanism of the rock mass show a strong relationship. The rheological properties of the rock mass result in micro cracks and holes, which can develop over time. So, the surrounding rock’s elastic modulus gradually decreases.
It was put forward that the corresponding creep damage evolution equation can be described as [7-10]
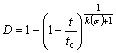 (2)
(2)
where D is the damage variable and tc is the rock mass failure time. According to the Refs. [10-12], k(σ) is the increasing function of stress; when stress is low, the damage evolution is faster. k(σ) can be expressed as follows:
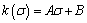 (3)
(3)
where A and B are test parameters.
The damage model considers the time effect and introduces the stress level influence. Therefore, it can better reflect the damage process.
In most geotechnical engineering, especially hard rock engineering, creep is only relevant in the first and second stages. However, tc describes the failure time. So, for creep processes of most rock mass, tc would lose its significance. It would be more universal to study the creep damage law of rock masses with a constant to represent tc.
Introducing the constant m, the damage evolution equation can be expressed as
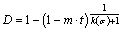 (4)
(4)
The one-dimensional creep damage equation can be described as
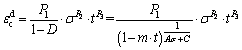 (5)
(5)
where C=B+1.
Under a three-dimensional stress state, the magnitude of deviatoric stress plays a decisive role in nonlinear creep. So, nonlinear creep can be expressed as follows:
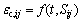 (6)
(6)
where 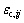 is the creep strain and Sij is the deviatoric stress.
is the creep strain and Sij is the deviatoric stress.
Under a three-dimensional stress state, deviatoric stress can be expressed as
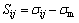 (7)
(7)
where 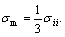
Deviatoric strain can be expressed as
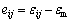 (8)
(8)
where 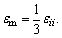
Under initial damage uniformity and isotropic damage, it is assumed that the elastic strain is caused by spherical tensor stress, and creep strain is caused by deviatoric tensor stress. So, the three-dimensional nonlinear creep damage model can be expressed as follows:
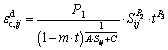 (9)
(9)
The three-dimensional nonlinear damage evolution model can be expressed as
 (10)
(10)
2.3 Test data fitting
According to Eq. (9), we can use the least square method to fit the experimental data and obtain the following parameters: P1=1.58×10-7, P2=2.14, P3=0.05, m=-26102, A=111.72, C=-6359.47.
Figure 3 shows the comparison of the fitting curve with the limestone specimen test curve under a 30 MPa confining pressure and different deviatoric stresses. The fitting curve obtained through the proposed nonlinear creep damage model displays good consistency with the rock creep test curve. Therefore, the proposed model can be used to reflect rock creep behavior.
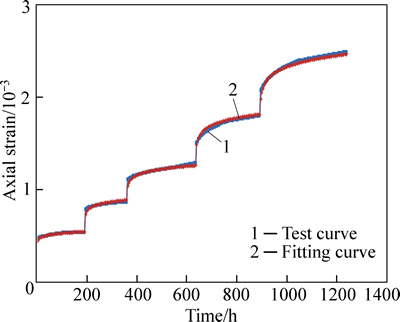
Fig. 3 Comparison of fitting curve with test curve
2.4 Numerical implementation of nonlinear creep damage model
Rock creep behavior is defined by a creep model provided by ABAQUS, and the plastic deformation follows the Drucker-Prager (D-P) model [13]. Rock creep is closely related to plastic deformation. Therefore, the definition of plasticity and plastic hardening must be included in the rock properties. The creep and plastic behavior is activated at the same time during the calculation process. So, the coupling method is used to solve the equation. The hyperbolic function, which is similar to the hyperbolic and exponential flow potential function in the plastic model, is adopted to represent the creep potential function. When the creep is defined, the hyperbolic plastic flow potential function is also used in the Drucker-Prager plastic model.
The hyperbolic flow potential function in the creep deformation direction is determined by the following equation:
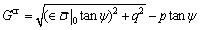 (11)
(11)
where 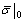 is the initial equivalent yield stress, and
is the initial equivalent yield stress, and 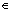 is the eccentricity that defines the rate at which the function approaches the asymptote.
is the eccentricity that defines the rate at which the function approaches the asymptote.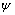 is the dilation angle measured in the p–q plane.
is the dilation angle measured in the p–q plane.
Rock mass plastic behavior is judged by the Drucker-Prager yield criterion provided by ABAQUS. The nonlinear creep damage constitutive model is programmed into the CREEP user subroutine and combined with ABAQUS to determine the creep’s coupling calculation, plasticity, and damage. Figure 4 shows the flow chart.
Rock mass variable damage can be calculated by programming USDFLD with a user subroutine that allows the user to define the field variables as the function of any of the output variables. This provides continuous updates during the calculation process. According to basic continuum damage mechanic principles, rock damage influence can be reflected by changing the elastic modulus, which can be expressed by 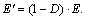 The damage variable is defined as the field variable, and the elastic modulus would be the function of the field variable. The field variable would be called once by a program during each iteration and through continuous field variable updates to control elastic modulus changes.
The damage variable is defined as the field variable, and the elastic modulus would be the function of the field variable. The field variable would be called once by a program during each iteration and through continuous field variable updates to control elastic modulus changes.
3 Mechanical properties of filling material
3.1 Developing new type of foam concrete filling material
Foam concrete is a lightweight concrete produced by blending foams in a foaming machine to make cement slurry, using the foaming machine’s pump system to make cast-in-situ construction or molding, and then make natural curing. In general, it is used as thermal insulation material in engineering construction. The deformation capacity of the foam is very good. However, it has many disadvantages such as large deformation under loads, water absorption, proclivity to crack, and low strength after deformation.
To overcome these shortages, a waterproofing agent, fiber, and other admixtures are blended into the foam concrete to improve its waterproof properties and ductility. The resulting foam concrete is waterproof, crack resistant, and maintains high strength after deformation. So, it can be used as a reserved deformation layer filling material for rheological rock mass tunnel construction.
3.2 Experimental study on mechanical properties
In this work, a uniaxial compression test of three foam concrete samples under a specific mixture ratio was conducted. Figure 5 shows that the foam concrete displays a uniaxial compressive strength of about 3.2 MPa. After the peak strength, its axial deformation increased continuously. Figure 6 shows the overall damage of the samples. Adding fibers to the foam concrete promoted strong connections in the aggregate, which allowed it to maintain its strength after deformation. As shown in Fig. 5, the sample strength after failure under a uniaxial compression test reached about 60% of the peak strength.
Figure 7 shows the test curves of the two foam concrete samples under hydrostatic pressure. The samples began to yield at hydrostatic pressure of 6.2 MPa. However, the sample strength did not reduce. Therefore, the samples showed elastic-plastic properties during the hydrostatic pressure test. Figure 8 shows the contrast of the samples before and after the test, which showed that the sample maintained its integrity after obvious deformation. This demonstrated that the new material had high ductility.
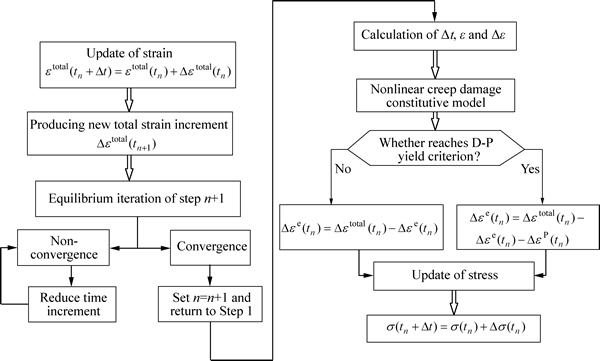
Fig. 4 Flow chart of CREEP user subroutine
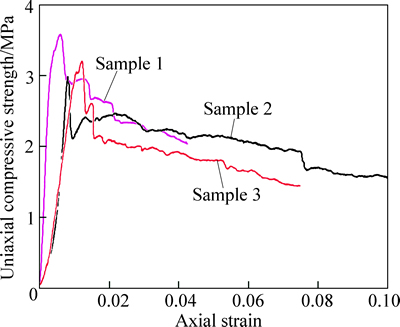
Fig. 5 Stress-strain curves of three samples of new foam concrete under a uniaxial compression test

Fig. 6 Damage mode of foam concrete under a uniaxial compression test
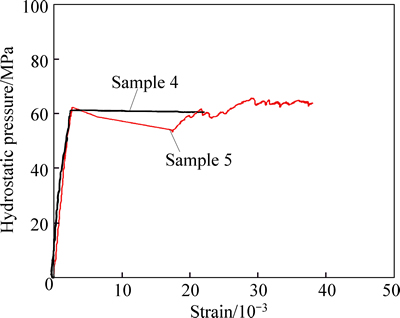
Fig. 7 Test curves of concrete foam samples under hydrostatic pressure

Fig. 8 Contrast of sample before (a) and after (b) hydrostatic pressure test
The uniaxial and triaxial tests showed that the concrete form had high deformability and ductility, and it could have higher strength and better integrity after deformation. Due to these properties, the concrete foam can be a promising filling material for deformation layers in tunnel construction in rheological rock masses.
3.3 Study of constitutive model
According to the uniaxial and triaxial test results, we used the crushable foam plasticity model to describe the mechanical properties of the foam concrete [14-16]. Figure 9 shows its yield surface in the p-q plane. The yield criterion expression can be rewritten as
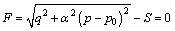 (12)
(12)
where p is the pressure stress, q is the Mises stress, S is the size of the q-axis of the yield ellipse, α is the shape factor of the yield ellipse that defines the relativemagnitude of the axes, 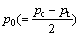 is the center of the yield ellipse on the p-axis, pt is the strength of the material in hydrostatic tension, and pc is the hydrostatic compression yield stress.
is the center of the yield ellipse on the p-axis, pt is the strength of the material in hydrostatic tension, and pc is the hydrostatic compression yield stress.

Fig. 9 Crushable foam plasticity yield surface model in p-q plane
The constant α can be determined using the initial yield stress in uniaxial compression 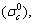 the initial yield stress in hydrostatic compression
the initial yield stress in hydrostatic compression 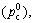 and the yield strength in hydrostatic tension (pt):
and the yield strength in hydrostatic tension (pt):
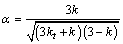 (13)
(13)
where 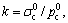 and
and 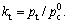
4 Reasonable deep tunnel support forms in hard rock masses
A tunnel which would be constructed in western China is composed of two carriage ways and sidewalk. The excavation width of design is 15.50 m. So, it belongs to the high-stress hard rock tunnel. The first and second linings are 20 cm and 40 cm thick, respectively. The reserved deformation layer of the new foam concrete is set between the first and second linings. Table 1 shows the properties of the surrounding rock and support materials, as shown in the on-site geological investigation report. Table 2 shows the mechanical parameters of the new foam concrete. The creep parameters of the surrounding rock are determined by fitting of the test data, which is introduced in Section 3.3.
Table 1 Properties of surrounding rock and support material
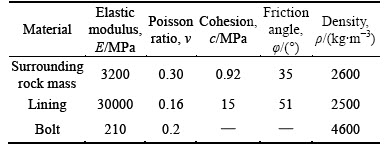
Table 2 Mechanical parameters of foam concrete

The appearance of plastic strain in the second lining after long-term tunnel use is an important evaluation index for judging tunnel stability [17-19]. Based on this idea, the minimum thickness of reserved deformation layer is used as the optimization goal and whether plastic strain appears in the second lining after creep of 100 years of surrounding rock is used as evaluation index to optimize the thickness the reserved deformation layer.
In general, when numerical simulations are compared with optimization schemes, modeling and calculation are made for different schemes [20-23]. This leads to lower accuracy in efficiency analysis. We propose a new staged optimization method to overcome these problems, described as follows:
1) Use the Python language to make secondary ABAQUS development to realize the finite element parametric modeling and automatic analysis of the calculation results. Then, this method is used to establish the parametric model, which could simulate the different thickness of the reserved deformation layer and automatically analyze the different calculation results. Figure 10 shows the parametric model, in which the reserved deformation layer thickness can change automatically.
2) Embed the finite element parametric design into the optimization algorithms based on MATLAB. Write an optimization program, which can change the reserved deformation layer thickness and judge whether or not plastic strain appears in the second lining.
Figure 11 shows the optimization analysis process.
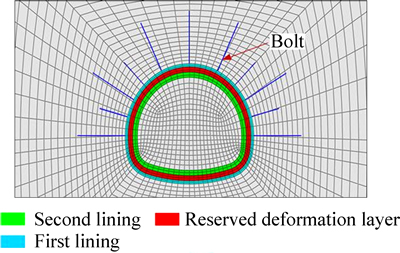
Fig. 10 parametric tunnel model
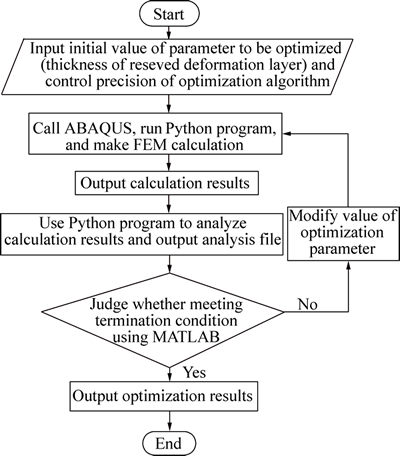
Fig. 11 Optimization analysis process
Through reserved deformation layer thickness staged optimization, it can be found that there was no plastic strain in the second lining when the minimum thickness of the reserved deformation layer was 28.50 cm. Figure 12 shows the plastic zone distribution in the second lining after 100 years of tunnel operation when there was no reserved deformation layer and the thickness of the reserved deformation layer was 28.50 cm. Table 3 shows the key deformation points in the second lining after 100 years of surrounding rock creep for both cases.
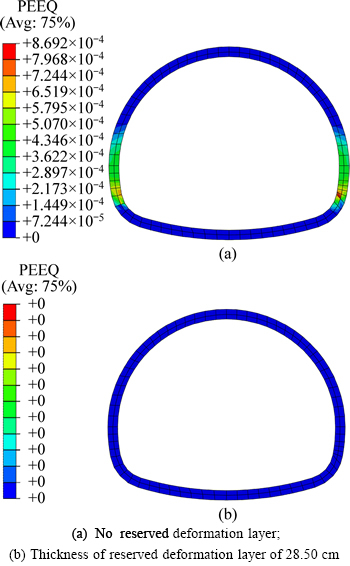
Fig. 12 Comparison of plastic zone distribution in second lining after 100 years of tunnel operation:
Table 3 Key deformation points in second lining after 100 years of surrounding rock creep for both cases
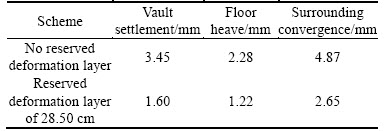
From Table 3, it can be found that with no reserved deformation layer, the vault settlement of the second lining was about 3.45 mm, the floor heave was 2.28 mm, and the surrounding convergence was 4.87mm after 100 years of surrounding rock creep. When the reserved deformation layer was 28.50 cm thick, key point deformation was obviously reduced. The vault settlement of the second lining was about 1.6 mm, the floor heave was 1.22 mm, and the surrounding convergence was 2.65 mm.
From Fig. 12, it can be found that with no reserved deformation layer, there was a large plastic zone area in the second lining after 100 years of surrounding rock creep. It mainly distributes on the both sides of hance and the maximum equivalent plastic strain is 0.00087. There was no plastic zone in the second lining when the reserved deformation layer was 28.50 cm thick.
Through the comparison, it can be found that the reserved deformation layer of the new foam concrete can absorb creep deformation for a long time to protect the second lining. Therefore, it can improve second lining stress and deformation to prevent plastic strain.
5 Conclusions
1) We use laboratory triaxial compressive rheological tests on limestone to study the nonlinear creep damage characteristics of surrounding rock masses for construction projects, thus establishing a nonlinear creep damage constitutive model for high-stress hard rock. The constitutive model creates fitting test curves and reveals corresponding creep parameters. Then, we use a program to make numerical implementations of the constitutive model using ABAQUS.
2) Uniaxial and triaxial compression tests of the foam concrete reveal that it has high strength and integrity after significant deformation. Therefore, this foam concrete can be an effective material for reserved deformation layers in construction tunnels in rheological rock masses. Meanwhile, we put forward a numerical calculation model that is suitable for the material.
3) We use reserved deformation layer minimum thickness as the optimization goal, and the appearance of plastic strain in the second lining after 100 years of surrounding rock creep as an evaluation index. We adopt the optimization method proposed in this work to stage optimization analysis of the reserved deformation layer thickness. The optimal reserved deformation layer thickness is found to be 28.50 cm. By comparing the results, it can be found that the reserved deformation layer with the foam concrete can effectively absorb creep deformation over a long period to reduce second lining deformation and prevent plastic zones from forming. Consequently, the second linings can be more stable and have more longevity.
References
[1] BRANTUT N, HEAP M J, MEREDITH P G, BAUD P. Time-dependent cracking and brittle creep in crustal rocks: A review [J]. Journal of Structural Geology, 2013, 52(1): 17-43.
[2] ZHOU Xiao-ping, HOU Qing-hong, QIAN Qi-hu, ZHANG Yong-xing. The zonal disintegration mechanism of surrounding rock around deep spherical tunnels under hydrostatic pressure condition: A non-Euclidean continuum damage model [J]. Acta Mechanica Solida Sinica, 2013, 26(4): 373-387.
[3] MALAN D F. Time-dependent behaviour of deep level tabular excavations in hard rock [J]. Rock Mechanics and Rock Engineering, 1999, 32(2): 123-155.
[4] ZHANG Yu, XU Wei-ya, GU Jin-jian, WANG Wei. Triaxial creep tests of weak sandstone from fracture zone of high dam foundation [J]. Journal of Central South University, 2013, 20(9): 2528-2536.
[5] NOMIKOS P, RAHMANNEJAD R, SOFIANOS A. Supported axisymmetric tunnels within linear viscoelastic burgers rocks [J]. Rock Mechanics and Rock Engineering, 2011, 44(5): 553-564.
[6] SHAO Jian-fu, CHAU K T, FENG X T. Modeling of anisotropic damage and creep deformation in brittle rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(4): 582-592.
[7] LIN Jie-wei, ZHANG Jun-hong, ZHANG Gui-chang, NI Guang-jian, BI Feng-rong. Aero-engine blade fatigue analysis based on nonlinear continuum damage model using neural networks [J]. Chinese Journal of Mechanical Engineering, 2012, 25(2): 338-345.
[8] ROSSIKHIN Y A, SHITIKOVA M V. Free damped vibrations of a viscoelastic oscillator based on Rabotnov's model [J]. Mechanics of Time-Dependent Materials, 2008, 12(2): 129-149.
[9] ZHANG Cheng-qing. Granite in the damage evolution of the stress wave effect of experimental research [D]. Beijing: China University of Mining & Technology, 2014. (in Chinese)
[10] LOKOSHCHENKO A M. Results of studying creep and long-term strength of metals at the Institute of Mechanics at the Lomonosov Moscow State University [J]. Journal of Applied Mechanics and Technical Physics, 2014, 55(1): 118-135.
[11] LEMAITRE J. A course on damage mechanics [M]. Springer Verlag, 1992: 87-95.
[12] DENG Bin, SHEN Zhi-bin, DUAN Jing-bo, TANG Guo-jin. Finite element method for viscoelastic medium with damage and the application to structural analysis of solid rocket motor grain [J]. Science China (Physics, Mechanics & Astronomy), 2014, 57(5): 908-915.
[13] HIBBITT D, KARLSSON B, SORENSEN P. ABAQUS/Standard user subroutines reference manual [M]. USA: The Pennsylvania State University, 2003: 50-62.
[14] MA Yu-li, SU Xian-yue, PYRZ R, RAUHE J C. A novel theory of effective mechanical properties of closed-cell foam materials [J]. Acta Mechanica Solida Sinica, 2013, 26(6): 559-569.
[15] CHRISTENSEN R M. Mechanics of cellular and other low-density materials [J]. International Journal of Solids and Structures, 2000, 37(1): 93-104.
[16] GIBSON L J, ASHBY M F. Cellular solids: Structure and properties [M]. Oxford: Pergamon Press, 1988: 108-121.
[17] GARSTECKI A, GLEMA A, LODYGOWSKI T. Sensitivity of plastic strain localization zones to boundary and initial conditions [J]. Computational Mechanics, 2003, 30(2): 164-169.
[18] YANG Xiao-li, JIN Qi-yun, MA Jun-qiu. Pressure from surrounding rock of three shallow tunnels with large section and small spacing [J]. Journal of Central South University, 2012, 19(8): 2380-2385.
[19] YANG Xiao-li, ZHANG Jia-hua, JIN Qi-yun, MA Jun-qiu. Analytical solution to rock pressure acting on three shallow tunnels subjected to unsymmetrical loads [J]. Journal of Central South University, 2013, 20(2): 528-535.
[20] HAGE C F, SHAHROUR I. Numerical analysis of the interaction between twin-tunnels: Influence of the relative position and construction procedure [J]. Tunnelling and Underground Space Technology, 2008, 23(2): 210-214.
[21] ADDENBROOKE T I, POTTS D M. Twin tunnel interaction: Surface and subsurface effects [J]. International Journal of Geomechanics, 2001, 1(2): 249-271.
[22] KARAKUS M, OZSAN A, BASARIR H. Finite element analysis for the twin metro tunnel constructed in Ankara Clay-Turkey [J]. Bulletin of Engineering Geology and the Environment, 2007, 66(1): 71-79.
[23] LEE Y Z, SCHUBERT W. Determination of the round length for tunnel excavation in weak rock [J]. Tunnelling and Underground Space Technology, 2008, 23(3): 221-231.
(Edited by YANG Bing)
Foundation item: Projects(51409154, 41372289 ) supported by the National Natural Science Foundation of China; Projects(2015JQJH106, 2014TDJH103) supported by Research Fund of Shandong University of Science and Technology, China
Received date: 2015-01-26; Accepted date: 2015-06-11
Corresponding author: WANG Qing-biao, Associate Professor, PhD; Tel: +86-538-3078249; E-mail: 53105189@qq.com