J. Cent. South Univ. (2017) 24: 967-976
DOI: 10.1007/s11771-017-3499-4
One-dimensional large-strain consolidation of soft clay with non-Darcian flow and nonlinear compression and permeability of soil
LI Chuan-xun(李传勋)1, WANG Chang-jian(王昌建)1, LU Meng-meng(卢萌盟)2,
LU Jian-fei(陆建飞)1, XIE Kang-he(谢康和)3
1. Faculty of Civil Engineering and Mechanics, Jiangsu University, Zhenjiang 212013, China;
2. School of Mechanics and Civil Engineering, China University of Mining and Technology, Xuzhou 221116, China;
3. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract: Geometrical nonlinearity of the soft soil and the deviation of water flow in the soft clay from Darcy’s law have been well recognized in practice. However, the theory of consolidation, which can account for both the geometrical nonlinearity and the non-Darcian flow, has not been reported so far. In this contribution, a model for the consolidation of soft clay which can allow for these two factors simultaneously is proposed. Utilizing the finite difference method, the numerical model for this problem is developed. With the numerical model, the effects of the geometrical nonlinearity and the non-Darcian flow on the consolidation of the soft soil are investigated. The results show that when the self-weight stress is calculated by the same method, the rate of the non-Darcian consolidation for the large-strain case is larger than that for the small-strain case, but the difference between them is limited. However, the difference between the consolidation rates caused by the non-Darcian and Darcian flows is significant. Therefore, when the geometrical nonlinearity of the soft clay is considered in calculating the consolidation settlement, due to the complexity of the large-strain assumption, the small-strain assumption can be used to replace it if the self-weight stress for the small-strain assumption is calculated by considering its sedimentation. However, due to the aforementioned large difference between the consolidation rates with consideration of the non-Darcian flow in soft clay or not, it is better to consider the non-Darcian flow law for both the small and large stain assumptions.
Key words: large-strain consolidation; non-Darcian flow; nonlinear compression; nonlinear permeability
1 Introduction
Since Darcy’s flow law was initially established for coarse-grained soils, it has been widely adopted in the consolidation theory of soft clay for its simplicity. However, the applicability of the Darcy’s law for fine-grained soils still maintains a controversial issue. In practice, for fine-grained soils under low hydraulic gradients, the deviation of water flow from Darcy’s law has been confirmed in some studies [1-4], which was called non-Darcian flow [1]. Based on the results obtained from some permeability tests and field measurements of settlement, the relationship between average relative velocity of pore water to soil particles, v, and hydraulic gradient, i, proposed by HANSBO [1] in 1960, can be seen in Fig. 1.
This relationship can be expressed as follows:
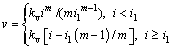 (1)
(1)
where kv is the coefficient of permeability; i1 is the critical value of hydraulic gradient; and m is the exponent of exponential relation at gradients lower than i1.
For this reason, it has a theoretical and practical significance to study the consolidation of fine-grained soils by incorporating this non-Darcian flow. In fact, some studies have consequently been focused on this issue [5-9]. All of the previous studies of consolidation, however, were based on the small-strain assumption, which may be unsuitable for a thick soft clay layer, especially for the silty clay, which is well known to experience a large settlement deformation during the consolidation process. Since GIBSON et al [10] set up the governing equation of one-dimensional large-strain consolidation, in which the void ratio of soil was adopted as a variable and various studies were developed on the theory of large-strain consolidation in numerical and analytical ways [11-18]. However, all of these studies were based essentially on Darcy’s flow law, which, as stated above, may not be applicable to fine-grained clayey soil.
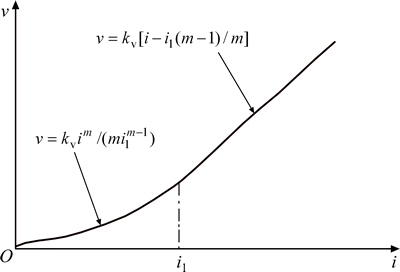
Fig. 1 Relationship between average velocity and hydraulic gradient
This paper presents a numerical solution for the consolidation of a soil layer with a large settlement deformation by including the non-Darcian flow law in Eq. (1) and the geometrical nonlinearity (i.e.,large-strain assumption) simutaneously. Some comparisons are made as well to investigate the large-strain consolidation with non-Darcian flow and Darcy’s flow law seperatly, and the non-Darcian consolidation with large-strain assumption and small-strain assumption seperatly.
2 Mathematical models for large-strain consolidation with non-Darcian flow
2.1 Description of large-strain consolidation with non-Darcian flow
As shown in Fig. 2, a saturated clayey soil layer is considered in both Lagrangian and convective coordinates, respectively. The direction of gravity is served as positive in both Lagrangian and convective coordinates, and the top surface of the clay layer can be referred as the datum plane in the convective coordinate ξ. The initial thickness of the clay layer is H. The top surface of the clay layer is pervious, and the bottom surface is pervious or impervious (PTPB or PTIB). The clay layer has been in equilibrium under both its self-weight and a previously external loading qp. The initial water level is higher than the datum plane, with a surplus-height of Hw. The top and bottom surfaces are noted as a=0 and a=H in Lagrangian coordinate and as ξ=S(0,t) and ξ=H in convective coordinate (where S(0, t) is the settlement of soft clay layer at time t), respectively. Figure 3 shows that the external load is applied instantaneously at the top surface of the clay layer with a value of qu.
2.2 Governing equation of large-strain consolidation with non-Darcian flow
Based on the study of GIBSON et al [10], the relationship between Lagrangian and convective coordinate can be expressed as
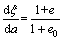 (2)
(2)
where e=e(a, t) is the void ratio of soil; e0= e(a, 0) is the initial void ratio of soil.
The hydraulic gradient i can be expressed in convective coordinate as follows:
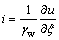 (3)
(3)
where γw is the unit weight of water; u is the excess pore water pressure in the clay layer.
Based on this, the hydraulic gradient i can be further expressed in Lagrangian coordinate as
 (4)
(4)
With consideration of the incompressibility of soil particle and pore water, according to the study by XIE and LEO [18], the general continuity condition governing 1-D large-strain consolidation in Lagrangian coordinate can be derived as
 (5)
(5)
where vw and vs are the velocities of pore water and soil particles relative to datum plane, respectively.
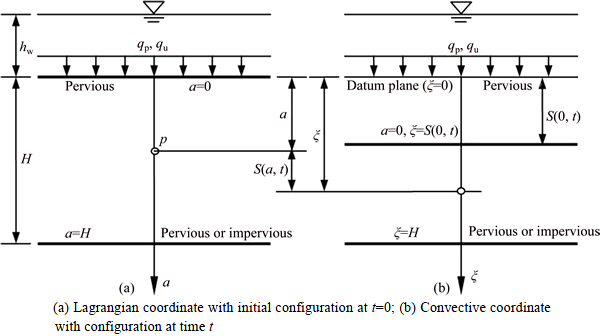
Fig. 2 Lagrangian and convective coordinates:

Fig. 3 Curve of external load qu vs time t
Herein, the creep effect of the soil skeleton is ignored and the consolidation is assumed to be monotonic. Thus, the void ratio is solely dependent on the effective stress and Eq. (5) can be then rewritten as
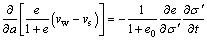 (6)
(6)
where σ′ is the effective vertical stress of clay layer.
The relations of some related variables have been given by XIE and LEO [18] in Lagrangian coordinate and are listed below:
 (7)
(7)
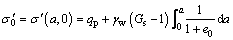 (8)
(8)
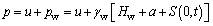 (9)
(9)
 (10)
(10)
where σ(a, t) is the total vertical stress; 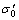 is the initial effective stress; p is the total pore water pressure; and pw is the static pore water pressure.
is the initial effective stress; p is the total pore water pressure; and pw is the static pore water pressure.
Since the external load qu is instantaneously applied, the following equation can be obtained by substituting Eq. (10) into Eq. (6):
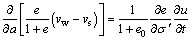 (11)
(11)
In combination with the definition of the average relative velocity of pore water to soil particle, Eq. (1) can be further expressed as
 (12)
(12)
Based on Eqs. (4), (11), and (12), the general equations governing 1-D large-strain consolidation of soft clay with non-Darcian flow in Lagrangian coordinate can be obtained as
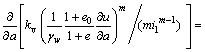
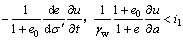 (13a)
(13a)
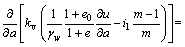
 (13b)
(13b)
The boundary condition for the top surface of the soil layer can be expressed as
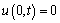 (14a)
(14a)
Meanwhile, the boundary condition for the impervious bottom and the pervious bottom can be given respectively as follows:
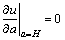 (14b)
(14b)
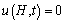 (14c)
(14c)
The initial condition for this problem has the following form:
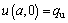 (14d)
(14d)
The coefficient of volume compressibility and the coefficient of permeability may decrease with the consolidation of soft clay, and the relationships of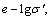
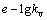 in Ref. [19], which is commonly used, is adopted here:
in Ref. [19], which is commonly used, is adopted here:
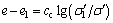 (15a)
(15a)
 (15b)
(15b)
where σ1′ is the current effective stress; e1 is the void ratio corresponding to σ1′; kv1 is the coefficient of permeability corresponding to e1; cc is the compressibility index; and ck is the permeability index.
The relationship between void ratio e and effective stress σ′ can be derived from Eq. (15a)
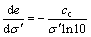 (16a)
(16a)
Combining Eqs. (15a) with (15b) generates:
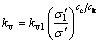 (16b)
(16b)
With substitution of Eqs. (16a) and (16b) into Eqs. (13a) and (13b), the governing equations can be rewritten as follows:
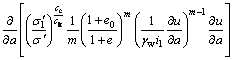 ·
·
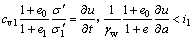 (17a)
(17a)
 ·
·
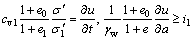 (17b)
(17b)
where 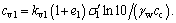
According to Eq. (15a), the initial void ratio e0 follows
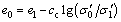 (18)
(18)
Substituting Eq. (18) into Eq. (8) and integrating gives
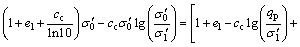
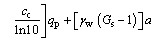 (19)
(19)
Since the initial effective stress 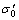 has been given by Eq. (19), the initial void ratio e0 also can be obtained.
has been given by Eq. (19), the initial void ratio e0 also can be obtained.
3 Numerical solutions for model
3.1 Dimensionless variables
To solve the governing equations numerically, the following dimensionless variables are firstly defined as
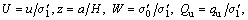
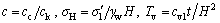 (20)
(20)
By utilizing above dimensionless variables, the governing Eqs. (17a)-(17b), boundary conditions Eqs. (14a)-(14c) and initial condition (14d) can be rearranged as
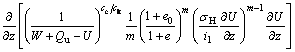 ·
·
 (21a)
(21a)
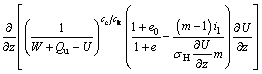 ·
·
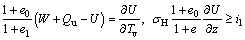 (21b)
(21b)
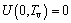 (Pervious top surface) (22a)
(Pervious top surface) (22a)
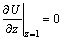 (Impervious bottom surface) (22b)
(Impervious bottom surface) (22b)
 (Pervious bottom surface) (22c)
(Pervious bottom surface) (22c)
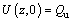 (Initial condition) (22d)
(Initial condition) (22d)
3.2 Finite difference solutions for excess pore water pressure
In order to solve the above equations numerically, a differential grid is placed in (z, Tv) -plane with a spatial step of △z. The jth nodal point of spatial domain is noted as zj, and zj=j△z, j=0, 1, 2, …, n. Dimensional value of initial effective stress at the jth nodal point, Wj, can be calculated by
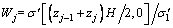
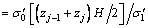 (23)
(23)
where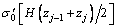 may be decided from Eq. (19), j=1, 2, 3, …, n.
may be decided from Eq. (19), j=1, 2, 3, …, n.
The initial void ratio of soil at the jth nodal point, e0j, can be derived from Eq. (18) as
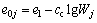 (24)
(24)
Meanwhile, the time domain is divided into a number of small time intervals. If the kth time interval is noted as △Tvk (k=0, 1, 2, …), the final time of the kth time interval, Tvk, is
 (25)
(25)
Similar to the previous study [8], the finite difference method is adopted and linearization technique is employed to obtain difference equation for quasi-linear diffusion equation. The difference equations corresponding to Eqs. (21a) and (21b) are as follows:
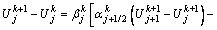
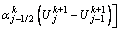 (26)
(26)
where 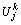 is the dimensionless value of excess pore water pressure for the jth spatial node point at Tv=Tvk; j=1, 2, …, n-1; k=0, 1, 2, …;
is the dimensionless value of excess pore water pressure for the jth spatial node point at Tv=Tvk; j=1, 2, …, n-1; k=0, 1, 2, …; 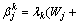
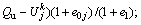
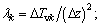
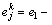
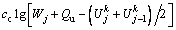 ;
;


The corresponding boundary conditions Eqs. (22a)- (22c) and the initial condition Eq. (22d) in terms of the dimensionless value of excess pore water pressure at the spatial node point are rewritten as follows:
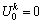 (Pervious top surface) (27a)
(Pervious top surface) (27a)
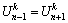 (Impervious bottom surface) (27b)
(Impervious bottom surface) (27b)
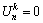 (Pervious bottom surface) (27c)
(Pervious bottom surface) (27c)
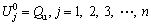 (Initial condition) (27d)
(Initial condition) (27d)
Using Eqs. (27a)-(27d), the differential Eq. (26) can be solved numerically to satisfy the solution conditions, which involves in solving a set of equations.
3.3 Finite difference solutions for settlement and average degree of consolidation
The relationship between Lagrangian coordinate and convective coordinate can be obtained from Fig. 2, and it follows
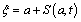 (28)
(28)
Differentiating Eq. (28) and substituting Eq. (2) into yields
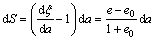 (29)
(29)
The settlement of clay layer St can be obtained by integrating Eq. (29) in the range of 0 to H:
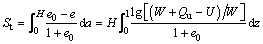 (30)
(30)
Substituting the values of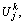 Wj and e0j into Eq. (30), the numerical solution for St at Tv=Tvk can be obtained:
Wj and e0j into Eq. (30), the numerical solution for St at Tv=Tvk can be obtained:
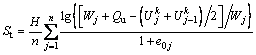 (31)
(31)
Based on the solution for St, the numerical solution for the final settlement of soft clay layer S∞ can be determined as
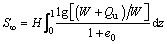
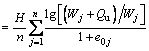 (32)
(32)
The average degree of consolidation in terms of deformation Us is defined as the ratio of the current settlement St to the final settlement S∞ as
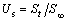 (33)
(33)
The average degree of consolidation in terms of stress Up is defined as the ratio of the average effective stress to the final average effective stress:
 (34)
(34)
4 Verification of aforementioned numerical methods
To verify the accuracy of the above numerical method, a comparison between XIE and LEO’s [18] analytical solutions with the corresponding numerical solutions is presented.
To obtain analytical solutions for large-strain consolidation, a relationship between the void ratio e and the coefficient of permeability kv was proposed by XIE and LEO [18] as
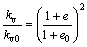 (35a)
(35a)
where kv0 is initial average coefficient of permeability in the whole clay layer.
Meanwhile, the coefficient of volume compressibility, mv1, also is assumed to maintain constant in the process of consolidation, i.e.,
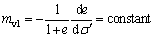 (35b)
(35b)
If Eqs. (15a) and (15b) is replaced by Eqs. (35a) and (35b), the governing equation of large-strain consolidation of soft clay with the non-Darcian flow is obtained as
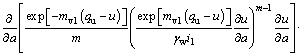
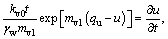
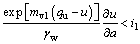 (36a)
(36a)
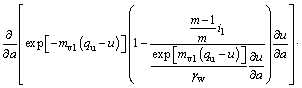
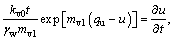
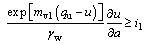 (36b)
(36b)
Based on Eqs. (36a) and (36b), the initial effective stress 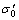 can be expressed as
can be expressed as
 (37)
(37)
where 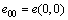 is the initial void ratio at the top surface of the clay layer.
is the initial void ratio at the top surface of the clay layer.
In this case, the initial void ratio of the clay layer e0 can be expressed as follows:
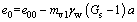 (38)
(38)
If m=1, Eqs. (36a) or (36b) can be reduced to the governing equation of large-strain consolidation with Darcy’s law, analytical solution of which has been obtained by XIE and LEO [18]. The same approach can be adopted to obtain the numerical solutions for Eqs. (36a) and (36b), and the numerical results are compared to the analytical solutions for the case of m=1. The parameters used in the following examples are specified in Table 1 and the difference grid is 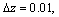
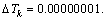
Table 1 Parameters used in large-strain consolidation with Darcy’s law

The comparison between the analytical and numerical solutions is presented in Table 2, which indicates the difference between them is negligible. Therefore, the numerical method adopted in this paper is reliable.
5 Analysis of consolidation behavior
Based on the above numerical methods, consolidation behavior of large-strain consolidation with non-Darcian flow law is investigated. The parameters of soft soil adopted in the analysis are specified in Table 3. The analysis is mainly performed to investigate the effects of Darcy’s and non-Darcian flow law on the large-strain consolidation, and the large- and small-strain assumptions on the non-Darcian consolidation.
5.1 Effects of Darcian and non-Darcian flow law on large -strain consolidation
As shown in Figs. 4 and 5, for both PTPB and PTIB models, the residual value of excess pore water pressure increases with an increase in the values of m or i1. The dissipation of excess pore water pressure with non- Darcian flow law may be slower than that with Darcy’s law, which corresponds to m=1 or i1=0.
As a result, Figs. 6 and 7 show that the average degree of consolidation defined in terms of excess pore water pressure, Up, decreases with an increase in the values of m or i1, for both the PTPB and PTIB models. In this case, if non-Darcian flow law is replaced by Darcy’s law, the error in the average degree of consolidation may become larger with an increase in the values of m or i1.
According to Eq. (15a) and combing the definition of the effective stress, the settlement deformation, which is determined by the variation of void ratio e, is dependent on the dissipation of the excess pore water pressure. Therefore, the average degree of consolidation defined in terms of settlement, Us, should be the same as that in terms of excess pore water pressure, Up (Figs. 8 and 9). In other words, the average degree of consolidation defined in terms of settlement also decreases with an increase in the values of m or i1, for both the PTPB and PTIB models. However, it is worth noting that the final settlement of soft clay layer is irrelevant to the values of m and i1 and remains as a constant. Therefore, the values of m and i1 may have an influence only on the dissipation of excess pore water pressure, but not on the final effective stress which decides the final settlement.
Table 2 Comparison results between numerical solutions and analytical solutions
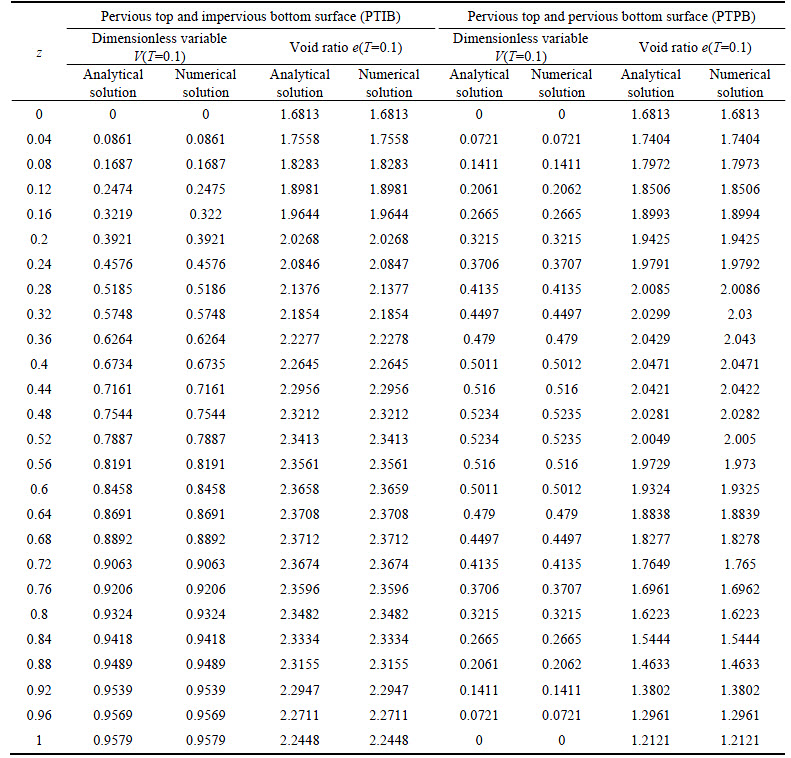
Table 3 Parameters of soft soil in analysis of consolidation behavior

5.2 Effects of large- and small-strain assumptions on non-Darcian consolidation
From Fig. 10, it can be seen that the dissipation of excess pore water pressure at the condition of large-strain
may be faster than that at the condition of small-strain. As indicated by Fig. 11(a), the settlement rate with large-strain assumption may also be faster than that with small-strain assumption. It may result from the fact that the thickness of soft soil layer becomes increasingly thinner and thinner during the process of consolidation for the sake of the large-strain assumption. However, it should be noted that, for the small-strain and large-strain assumptions, the final settlement of soil layer is the same, and moreover, the difference in the consolidation curves is notably small. Likewise, the error induced by the neglect of the geometric nonlinearity of soil in predicting the consolidation rate also seems to be very small, even when the compression index of the soil increases up to 1.2756 ( as shown in Fig. 11(b) ).
It is well known that self-weight stress has a great influence on the nonlinear consolidation behavior of a soft soil layer for both large-strain and small-strain assumption. Further studies on the influence of initial effective stress on consolidation behavior are presented, in which the self-weight stress in small-strain consolidation is considered in several ways as follows:
Case 1: The sedimentation of clay is considered and just as Eq. (19), self-weigh stress increases with depth nonlinearly. It is worth to note that the self-weight stress in all above consolidation behavior analysis is determined by Eq. (19),
Case 2: Self-weight stress is proposed to increase with depth linearly. In this case, the effective unit-weight γ′ is assumed to maintain constant, and the initial effective 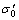 is
is
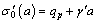 (39)
(39)
Case 3: Self-weight stress is proposed to maintain constant with depth, and the value is usually equal to the average value of Case 2, that is
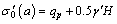 (40)
(40)
Figure 12 confirms that the difference between the consolidation curves for large-strain and small-strain assumptions is very limited, if both of the initial effective stresses are determined by Eq. (19). In addition, the final settlement may be same for both assumptions. On the country, if the initial effective stress is determined by different methods in small-strain consolidation, the difference is evident. Moreover, the final settlement may be different as well. For this reason, if the initial effective stress is calculated by using Eq. (19) at the assumption of both large-strain and small-strain, the error induced from the neglect of the geometric nonlinearity of soil in predicting the consolidation rate seems to be notably small. Therefore, the difference in the consolidation rate between large-strain and small-strain assumptions, which has been reported in the previous literature, is mainly inducted from the calculation method of initial effective stress (i.e., self-weight stress).

Fig. 4 Influence of parameter m on dissipation of excess pore water pressure:
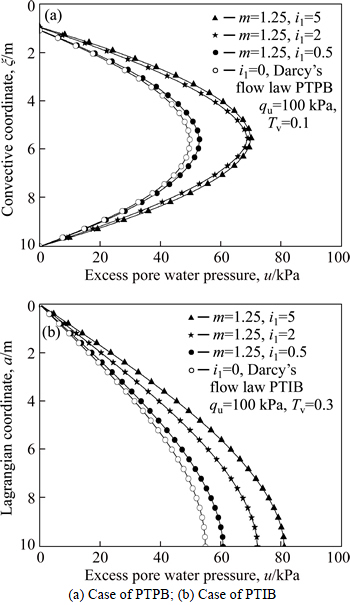
Fig. 5 Influence of parameter i1 on dissipation of excess pore water pressure:
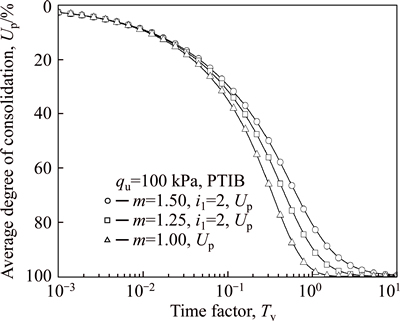
Fig. 6 Influence of m on Up
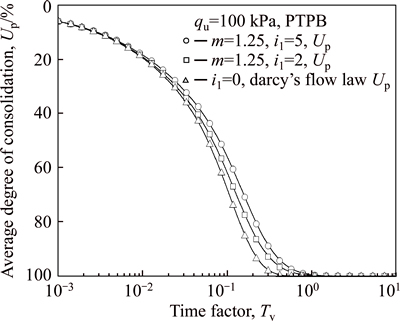
Fig. 7 Influence of i1 on Up
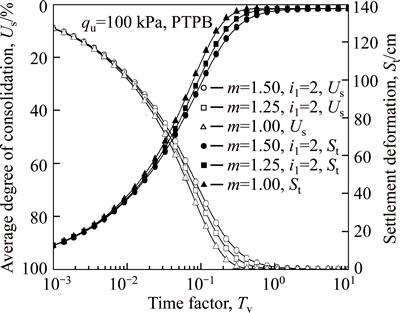
Fig. 8 Influence of m on Us and St
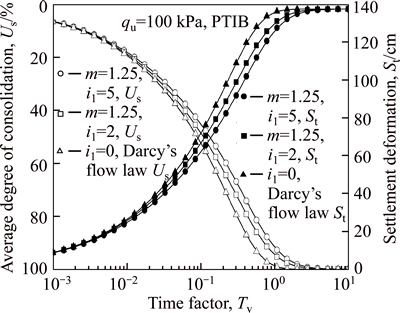
Fig. 9 Influence of i1 on Us and St
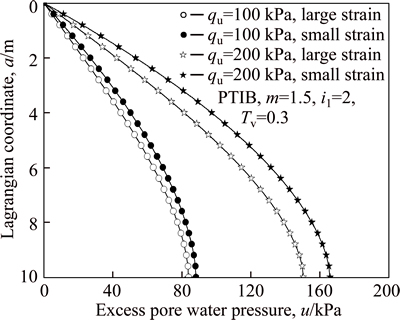
Fig. 10 Difference in dissipation of pore water pressure between large-strain and small-strain consolidation
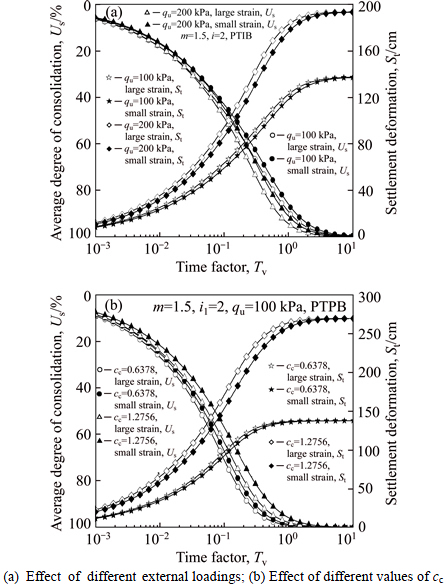
Fig. 11 Difference of settlement deformation between large- strain and small-strain consolidations:
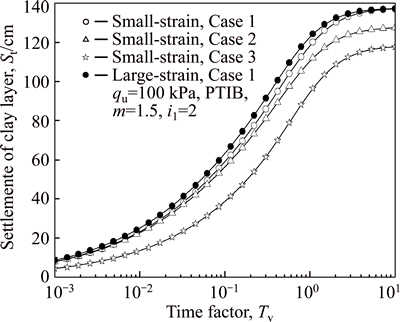
Fig. 12 Effects of self-weight stress on large- and small-strain consolidations of clay with non-Darcian flow
As shown in Fig. 13, if non-Darcian flow law in soft soil is ignored, the error induced from the neglect of non-Darcian flow law in predicting the consolidation rate may be more significant than that induced from the neglect of geometrical nonlinearity. Therefore, if the water flow deviates from Darcy’s law, the non-Darcian flow law should be considered. Meanwhile, if the initial effective stress is calculated by Eq. (19) for both thelarge-strain and small-strain assumptions, the geometric nonlinearity can be ignored to avoid the complexity of governing equation.
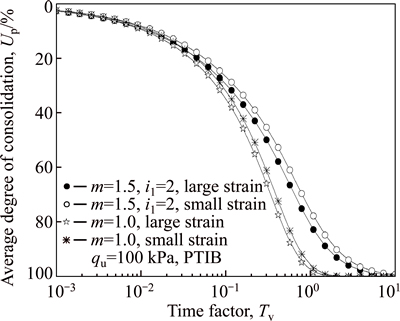
Fig. 13 Influence of non-Darcian flow and geometric nonlinearity on consolidation behavior
6 Conclusions
A mathematical model which governs one- dimensional large-strain consolidation of soft clay with non-Darcian flow is derived. The numerical solutions for this mathematical model are then obtained using the finite difference method. The effects of non-Darcian flow and geometrical nonlinearity of soft clay on the consolidation behavior are analyzed. The results show the consolidation rate for large-strain assumption with non-Darcian flow (adopted in this work) may be slower than that with Darcy’s flow law, and it decreases with an increase in the values of m and i1. Moreover, the difference in the consolidation rate between non-Darcian flow and Darcian flow law is evident. When the initial effective stress is calculated by considering the sedimentation of clay, the final settlement with large-strain assumption is the same as that with small-strain assumption. Since the consolidation rate for large-strain assumption is faster than that for small-strain assumption, the error in consolidation rate induced from replacing the large-strain assumption by small-strain assumption is very limited, which brings a great convenience into the analysis of large-strain consolidation problem because the small-strain analysis is much simple in engineering practice.
References
[1] HANSBO S. Consolidation of clay, with special reference to influence of vertical sand drains [C]// Swedish Geotechnical Institute Proceeding. Stockholm: Swedish Geotechnical Institute, 1960: 45-50.
[2] DUBIN B, MOULIN G. Influence of a critical gradient on the consolidation of clays [C]// YONG R N, TOWNSEND F C. Consolidation of Soils: Testing and Evaluation (STP 892). ASTM, 1985: 354-377.
[3] HANSBO S. Consolidation equation valid for both Darcian and non-Darcian flow [J]. Geotechnique, 2001, 51(1): 51-54.
[4] HANSBO S. Deviation from Darcy’s law observed in one- dimensional consolidation [J]. Geotechnique, 2003, 53(6): 601-605.
[5] TEH C I, NIE X Y. Coupled consolidation theory with non-Darcian flow [J]. Computers and Geotechnics. 2002, 29(3): 169-209.
[6] LI C X, XIE K H, WANG K. Analysis of 1D consolidation with non-Darcian flow described by exponent and threshold gradient [J]. Journal of Zhejiang University: Science A, 2010, 11(9): 656-667.
[7] LI C X, XIE K H, HU A F, HU B X. Analysis of one-dimensional consolidation of double-layered soil with non-Darcian flow described by exponent and threshold gradient [J]. Journal of Central South University, 2012, 19(2): 562-571.
[8] LI C X, XIE K H. One-dimensional nonlinear consolidation of soft clay with the non-Darcian flow [J]. Journal of Zhejiang University: Science A, 2013, 14(6): 435-446.
[9] WALKER R, INDRARATNA B, RUJIKIATKAMJORN C. Vertical drain consolidation with non-Darcian flow and void-ratio dependent compressibility and permeability [J]. Geotechnique, 2012, 62(11): 985-997.
[10] GIBSON R E, ENGLAND G L, HUSSEY M J L. The theory of one-dimensional consolidation of saturated clays: I. Finite non-linear consolidation of thin homogeneous layers [J]. Geotechnique, 1967, 17(2): 261-273.
[11] MONTE J L, KRIZEK R J. One-dimensional mathematical model for large-strain consolidation [J]. Geotechnique, 1976, 26(3): 495-510.
[12] GIBSON R E, SCHIFFMAN R L, CARGILL K W. The theory of one-dimensional consolidation of saturated clays: II. Finite non-linear consolidation of thick homogeneous layers [J]. Canadian Geotechnical Journal, 1981, 18(2): 280-293.
[13] CARGILL K W. Prediction of consolidation of very soft soil [J]. Journal of Geotechnical Engineering, ASCE, 1984, 110(6): 775-795.
[14] TAN T S, SCOTT R F. Finite strain consolidation-a study of convection [J]. Soils and Foundations, 1988, 28(3): 64-74.
[15] TOWNSEND F C, MC VAY M C. SOA: Large strain consolidation prediction [J]. Journal of Geotechnical Engineering, ASCE, 1990, 116(2): 222-243.
[16] CHOPRA M B, DARGUSH G F. Finite element analysis of time dependent large deformation problems [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1992, 16(2): 101-130.
[17] MORRIS P H. Analytical solutions of linear finite-strain one-dimensional consolidation [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(4): 319-326.
[18] XIE K H, LEO C J. Analytical solutions of one-dimensional large strain consolidation of saturated and homogeneous clays [J]. Computers and Geotechnics, 2004, 31(4): 301-314.
[19] MESRI G, ROKHSAR A. Theory of consolidation for clays [J]. Journal of the Soil Mechanics and Foundation Division, ASCE, 1974, 100(Gt8): 889-904.
(Edited by YANG Hua)
Cite this article as: LI Chuan-xun, WANG Chang-jian, LU Meng-meng, LU Jian-fei, XIE Kang-he. One-dimensional large-strain consolidation of soft clay with non-Darcian flow and nonlinear compression and permeability of soil [J]. Journal of Central South University, 2017, 24(4): 967-976. DOI: 10.1007/s11771-017-3499-4.
Foundation item: Projects(51109092, 11272137) supported by the National Natural Science Foundation of China; Projects(2013M530237, 2014T70479) supported by China Postdoctoral Science Foundation; Project(SJLX15-0498) supported by Jiangsu Provincial Graduate Students Research and Innovation Program, China
Received date: 2015-05-06; Accepted date: 2016-12-01
Corresponding author: LI Chuan-xun, Associate Professor, PhD; Tel: +86-511-88791351; E-mail: lichuanxun@yeah.net