DOI:10.19476/j.ysxb.1004.0609.2018.05.22
原地浸矿单孔注液影响半径的计算模型
桂 勇1,王观石2, 3,赖远明2,洪本根1,胡世丽3,龙 平1
(1. 江西理工大学 资源与环境工程学院,赣州 341000;
2. 中国科学院 寒区旱区环境与工程研究所,兰州 730000;
3. 江西理工大学 建筑与测绘工程学院,赣州 341000)
摘 要:掌握稳渗状态下单孔注液的影响半径对于合理确定注液孔的孔网参数具有重要意义。假设注液孔孔底以上湿润体为椭球体,基于注液孔孔周入渗强度等于注液孔孔底影响范围内的下渗强度,建立稳渗状态下单孔注液影响半径的计算模型;现场试验获得5种注液强度条件下的孔中液面高度和影响半径,并与模型计算结果进行比较。结果表明:采用该模型计算得到的影响半径与现场试验得到的影响半径的最大误差为8.14%,满足工程要求,表明单孔注液影响半径计算模型是有效的;当注液孔半径小于0.2 m时,随注液孔半径增加,影响半径成非线性增加;当注液孔半径大于0.2 m时,随注液孔半径增加,影响半径近似成线性增加;当注液孔半径为0.1 m和孔中液面高度不超过3 m时,注液孔影响半径与孔中液面高度近似成线性关系。
关键词:原地浸矿;注液孔;影响半径;离子型稀土
文章编号:1004-0609(2018)-05-1050-09 中图分类号:TD865 文献标志码:A
原地浸矿是提取离子型稀土资源的第三代工艺[1],该工艺通过注液孔向矿体注入浸矿剂溶液,使其与稀土离子发生交换反应,再在注液孔注入上清液,稀土离子进入上清液中形成浸出液,浸出液从收液工程流出,用沉淀剂沉淀浸出液中的稀土离子,实现资源回收的目的[2]。在推广原地浸矿工艺20多年的过程中,也暴露出该工艺的不足,如网孔布置主要依赖于经验。
网孔布置的合理与否将直接影响到稀土资源回收率[3-4],主要表现在两个方面。一方面,注液孔间距布置过大,在注液强度一定的情况下,浸矿剂不能入渗到更远的区域,容易造成浸矿盲区,降低稀土资源回收率;另一方面,注液孔间距布置过小,就会加大投入成本,同时也容易造成窜孔现象,一旦发生窜孔,进一步增加浸矿盲区范围,降低资源回收率;另外,注液孔间距太小,容易造成注液强度偏大,进而容易发生滑坡[5-6],滑坡区域的资源也难以回收。
一般来说,原地浸矿注液孔的影响范围内处于非饱和状态,浸矿剂溶液的入渗过程不仅受到重力作用和孔内水压力作用,同时还受到矿体的基质吸力作用。有关地表水从饱和区入渗至非饱和区,国内外学者已开展了大量研究,提出了饱和-非饱和渗流计算原理[7],以及具有不同特点和用途的入渗模型[8],其中Green-Ampt入渗模型因其具有明确的物理意义而得到了广泛的应用。但由于Green-Ampt入渗模型忽略非饱和区域存在的实际情况,张杰等[9]提出了基于分层假定的入渗模型。同时为了使这些地表水入渗模型的计算结果与试验符合得更好,尹升华等[10]提出入渗率与入渗水头的关系,何丹等[11]研究了土壤物理力学参数变异条件下的入渗规律,赵伟霞等[12]建立了地表水从井(孔)中入渗至土壤的简化模型。由于原地浸矿的注液孔具有自身的特殊性,如孔半径为0.1~0.2 m,孔中积水深度为0.5~1.0 m等,运用现有的模型难以分析注液孔的影响半径和浸矿盲区。
本文作者根据现场亮蓝示踪试验结果,假设注液孔孔底以上湿润体为椭球体,基于注液孔孔周入渗强度等于注液孔孔底影响范围内的下渗强度,建立了稳渗状态下单孔注液影响半径的计算模型,该模型为合理确定原地浸矿工艺的注液孔孔网参数提供依据。
1 单孔注液影响半径的计算模型
1.1 注液孔的湿润体
为建立单孔注液影响半径的计算模型,在江西龙南足洞矿区开展单孔注液的亮蓝染色示踪试验。在试验矿山选择一处地势平整的试验点,采用洛阳铲钻取一个孔深2.0 m,孔半径0.09 m的注液孔,之后在注液孔内注入浓度为4.0 g/L的亮蓝溶液,单孔注液强度为1.2 m3/d,注液量为2.4 m3。注液完成5 d后,以注液孔为中心,沿竖向开挖,染色范围如图1所示。从图1可以看出,注液孔孔底以上部分的染色范围近似为椭球体。

图1 单孔注液的染色范围
Fig. 1 Stain range of single-hole injection
基于单孔注液的染色示踪试验结果,提出建立单孔注液影响半径计算模型的基本假设:假设注液孔孔底以上部分的湿润体为椭球体,如图2所示,椭球面方程为
 (1)
(1)
式中:a为孔底平面上注液孔周与椭球面的距离;c为注液孔中积水深度;r为径向坐标;r0为注液孔半径;z为注液孔深度方向的坐标,向下为正方向。
1.2 孔周入渗强度
在注液孔孔底以上的湿润体内取一个微小圆环段,弧度为单位1,厚度为单位1,如图3所示。设注液孔半径为r0,当微小圆环段的深度方向坐标为z时,a′d′面为注液孔孔壁,受到的压力水头hk=c+z,水头方向垂直孔壁;b′c′面受到土体的基质吸力作用,负压水头值为hf,水头方向垂直椭球面向外。则计算得到微小圆环段单位弧度的平均渗流速度iz,其计算公式为
 (2)
(2)
式中:kd为圆环段的平均渗透系数;A1为微小圆环段a′d′面的面积,A1=r0×1;n为土体孔隙度;hf为负压水头值,可以根据实测土水特性曲线拟合得到;A2为b′c′面的面积, ;A为微小圆环段a′b′c′d′面的面积,
;A为微小圆环段a′b′c′d′面的面积, 。将A1、A2、A代入式(2)并简化可得深度为z处单位弧度的平均渗流 速度:
。将A1、A2、A代入式(2)并简化可得深度为z处单位弧度的平均渗流 速度:
 (3)
(3)

图2 单孔注液湿润体示意图
Fig. 2 Schematic diagram of wetted volume caused by single-hole injection
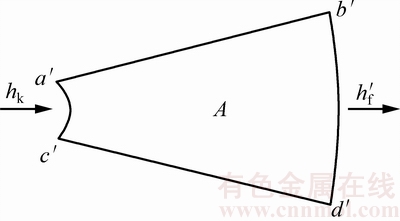
图3 微小圆环段示意图
Fig. 3 Schematic diagram of micro ring segment
令注液孔孔周对应的单位时间内单位弧度的入渗强度为I,对平均渗流速度iz在z方向(-c;0]上进行积分即为I,则I的计算公式为
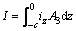 (4)
(4)
式中:A3为微小圆环段的平均截面面积, 。
。
将A3代入式(4)并简化可得注液孔孔周对应的单位时间内单位弧度的入渗强度:
 (5)
(5)
假设椭球面上的含水率相等,且体积含水率沿径向成负指数变化,即:
 (6)
(6)
式中:θs为饱和体积含水率;θi为初始体积含水率;b为反映含水率随径向距离变化快慢的常数。
根据文献[13],当饱和度大于80.0%时,砂性土就处于饱和状态。考虑到原地浸矿过程中,浸矿剂需要通过渗流过程才能进入矿体,因而渗流速度决定浸矿效率和浸矿速度,为此重点关注饱和度大于80.0%的区域,以饱和度80.0%以上湿润体为研究对象。
令在注液孔底所在平面上饱和度为80%的椭球面与注液孔周的距离为a1,椭球面上的体积含水率为θ1,对应的负压水头值为hf1,则影响半径R=a1+r0。
由式(6)可得a1的计算公式为
 (7)
(7)
由文献[14]可知,某一等含水率面上的平均基质吸力可基于非饱和土的土水特征曲线和渗透系数方程确定。根据文献[15]中湿润锋面上平均基质吸力的算法,类比饱和度为80%椭球面(等含水率面)上平均基质吸力的算法为
 (8)
(8)
式中:ψ为基质吸力;ψ1为饱和度80%椭球面的平均基质吸力;k为非饱和渗透系数;ψa1为饱和度80%所对应的基质吸力。
由van GENUCHTEN提出的经验公式[16]可知:
 (9)
(9)
式中:m为形状参数;S为土体相对饱和度,其计算公式为
 (10)
(10)
式中:θs为饱和体积含水率;θr为残余体积含水率;l、m、n为形状参数,且m=1-1/n,该3个参数可通过土水特征曲线获得。
由公式(8)、(9)和(10)可得饱和度为80%椭球面上平均基质吸力ψ1的计算公式,由此可得负压水头值hf1的计算公式:
 (11)
(11)
式中:ρw为水的密度;g为重力加速度。
由文献[17]可知,非饱和土的渗透性参数随体积含水率变化呈现非线性变化,含水率降低,渗透性快速降低。当土体的体积含水率由饱和体积含水率θs降低到饱和度80%所对应的体积含水率θ1时,湿润体内的平均渗透系数小于饱和渗透系数。由van GENUCHTEN提出的估算非饱和土体渗透系数的经验公式[16],可令平均渗透系数kd的计算公式为:
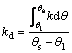 (12)
(12)
将式(7)、(11)、(12)代入式(5)便得到单位弧度孔周入渗强度I的计算公式。
1.3 孔底影响范围内的下渗强度
浸矿剂溶液进入矿体后,在重力作用下向下渗透,水力梯度j=1,注液孔孔底单位时间内单位弧度的径向距离r处溶液下渗强度为dQ,如图2所示。dQ的计算公式为
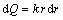 (13)
(13)
则注液孔底影响范围内单位时间单位弧度下渗强度Q的计算公式为
 (14)
(14)
为简化式(14)的计算,需要设定计算范围,假设注液孔底影响范围内含水率θ(a)满足如下关系式:
 (15)
(15)
由式(6)和式(15)可得a的计算公式:
 (16)
(16)
将式(9)、式(16)代入式(14)可得注液孔底影响区域内单位时间单位弧度下渗强度Q的计算公式。
稳渗状态时,在单位弧度和单位时间内,孔周的入渗强度等于注液孔底影响范围内的下渗强度,即I=Q,则根据式(5)和式(14)可以解出对应液面高度下的参数b,运用式(7)便可计算a1,由此可计算出单孔注液的影响半径R。
2 单孔注液的影响半径分析
2.1 土水特征曲线测试试验
原状矿体的土-水特征曲线测试地点位于江西省龙南县某离子型稀土矿山,试验前先将试验场地平整,利用环刀取样,通过室内土工试验测得该类型矿体的基本物理性质指标如表1所列。利用激光粒度分析仪测得该矿体的粒径累积曲线,如图4所示。根据表1的基本物理性质指标和图4颗粒级配累计曲线判定该离子型稀土矿的土体类型为粉砂。
根据表1中孔隙比e=0.92,可计算出饱和体积含水率θs=0.48,饱和度为80%等含水率面上的体积含水率θ1=0.38。
表1 离子型稀土矿体物理性质指标
Table 1 Physical property indexes of ion-type rare earth ore bodies


图4 颗粒级配累计曲线
Fig. 4 Cumulative curve of grain composition
土-水特征曲线的测试试验的现场是1个1 m×1 m的平面区域,如图5所示。测试仪器为TEN型张力计,长度为30 cm,可量测的基质吸力范围为0~100 kPa,本次试验共埋入8根张力计。仪器埋置完毕后,使其在土体中静置一段时间,待数据稳定后在观测读数,并取样测试不同张力计所对应的体积含水率,结果见表2。

图5 现场基质吸力试验
Fig. 5 Field test of matrix suction
表2 土-水特征曲线测试结果
Table 2 Test results of soil-water characteristic curve

土水特征曲线模型采用van Genuchten模型进行描述,其表达式为
 (17)
(17)
式中:各参数含义与式(10)相同。
采用van Genuchten模型拟合稀土矿体的土水特性曲线,并确定相关参数θr=0.09、l=12.30、n=1.97、m=0.49、决定系数为0.94、残差平方和为0.01。
2.2 单孔注液试验
本次现场单孔注液试验位于同一离子型稀土矿山,试验区域的坡度为12°~19°,表土层厚度为0.8~1.1 m。试验开始前,通过单环法测得注液孔所在区域的饱和渗透系数为1.08 m/d。
本次试验设定5种注液强度,分别为3.0、2.4、1.8、1.2、0.6 m3/d。在试验区域人工钻5个注液孔,孔深为2~3 m,孔半径为0.09 m。距离每个注液孔0.5、1.0、1.5、2.0、2.5、3.0 m处各钻1个孔,分别命名为1号孔、2号孔、3号孔、4号孔、5号孔、6号孔,孔内埋置型号为FDS-100水分传感器,用于记录不同位置处土壤体积含水率的变化,如图6所示。其中1号孔、2号孔、3号孔中埋置9个水分传感器, 4号孔、5号孔中埋置8个水分传感器,6号孔中埋置7个水分传感器,水分传感器的埋深及埋置位置如图7所示。
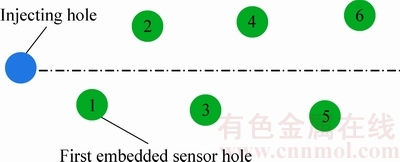
图6 水分传感器布置平面图
Fig. 6 Plane arrangement chart of moisture sensor
为使试验区域土体恢复至初始状态,仪器布置完毕后,静置2个月,随后开始向注液孔内连续注液。注液方式是由高位池引出1根PVC主管,在主管相应位置上分别引出1根PVC支管至对应的注液孔。为控制和记录注液量,在支管的出水口处安装1个水龙头和1个水表。
试验正式开始后,将各水分传感器连接至主机采集器,利用主机采集器记录土壤体积含水率的变化,数据采集时间间隔设定为3 min,同时利用数显型液位变送器记录注液孔内积水深度的变化。当注液孔周边90%以上水分传感器读数及孔中液面高度趋于稳定时,则认为该注液孔周边渗流达到稳定状态。注液10 d后达到稳渗状态,试验所得孔中液面高度和影响半径见表3。
表3 现场试验实测值
Table 3 Measured values of field test

2.3 试验结果与分析
2.3.1 模型的验证
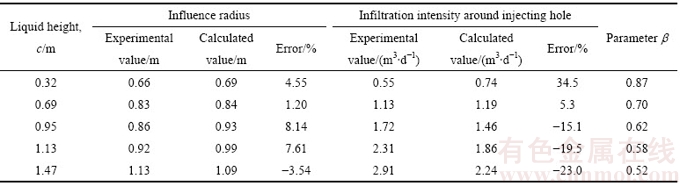
采用本模型计算得到试验条件下的注液强度和影响半径,详见表4。
由表4可看出,除液面高度为0.32 m时模型计算出的孔周入渗强度偏大外,其余液面高度下模型计算结果与现场试验结果的误差均在25%以内;同时考虑到原地浸矿技术规范中提出的注液孔深为见矿0.5~1.0 m,即要求注液孔中液面高度为0.5~1.0 m,该孔内液面深度范围内,误差均小于20%,因此可以认为满足工程要求,验证了计算模型的有效性。

图7 水分传感器布置剖面示意图
Fig. 7 Schematic diagram of profile arrangement about moisture sensor
表4 注液孔影响半径及孔周入渗强度的计算值与试验值
Table 4 Calculated value and experimental value of influence radius of injecting hole and infiltration intensity around injecting hole
2.3.2 注液孔半径与影响半径的关系
现讨论稳渗状态下影响半径随注液孔半径的变化规律。由模型计算的数据可得,液面高度为0.69 m、0.95 m、1.13 m 3种情况下,影响半径随注液孔半径的变化规律如图8所示。
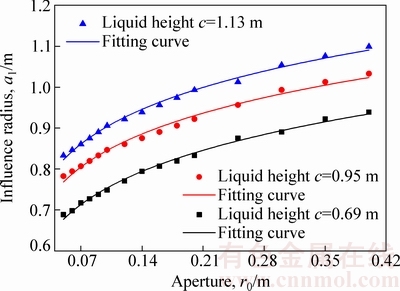
图8 注液孔径对影响半径的影响
Fig. 8 Influence of aperture on influence radius
从图8可以看出,当注液孔半径小于0.2 m时,随注液孔孔径增加,影响半径成非线性增加;当注液孔半径大于0.2 m时,随注液孔孔径增加,影响半径近似成线性增加。为进一步反映注液孔孔径对影响半径的影响,采用幂函数R=A′×r0B′(A′和B′为拟合参数)拟合影响半径与孔径的关系,拟合结果见表5,决定系数都大于0.98,拟合效果较好。影响半径对注液孔径求导数,导数值的大小可以作为设计注液孔大小的依据,导数值越大,表明注液孔的注液效率越高,由拟合结果计算得到影响半径对注液孔径的导数值与孔径的关系,如图9所示。图9表明,随注液孔径增加,注液效率降低;目前原地浸矿工程中的注液孔半径通常为0.1 m,此时影响半径对注液孔径的导数值大于1,具有较高的注液效率,表明现有的孔径设计是合理的。
表5 参数A′和B′的拟合结果
Table 5 Fitting results of parameters A′ and B′
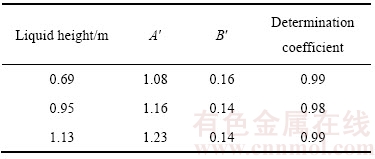

图9 影响半径对注液孔孔径的导数值与孔径的关系
Fig. 9 Relationship between derivative value of influence radius to aperture and aperture
2.3.3 孔内液面高度与影响半径的关系
现进一步讨论稳渗状态下影响半径随孔内液面高度的变化规律。当注液孔半径为0.1 m且孔中液面高度不超过3m时,采用本模型计算得到注液孔影响半径与孔径的关系,如图10所示。由图10可知,注液孔影响半径与孔中液面高度近似成线性关系,采用线性函数R=pc+q(m和n为拟合参数)影响半径与液面高度c的关系,拟合结果为p=0.54,q=0.29,决定系数为0.99,拟合效果较好。
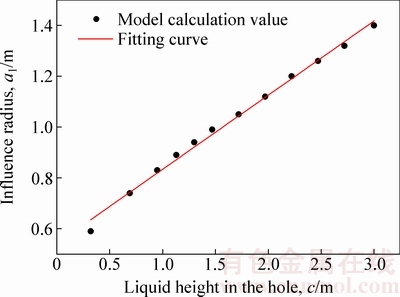
图10 孔内液面高度对影响半径的影响
Fig. 10 Influence of liquid height on influence radius
3 结论
1) 假设注液孔孔底以上湿润体为椭球体,基于注液孔孔周入渗强度等于注液孔孔底影响范围内的下渗强度,建立稳渗状态下单孔注液影响半径的计算模型,现场试验验证了该模型的有效性。
2) 现场试验获得5种注液强度条件下孔中液面高度和影响半径,采用本模型计算得到的影响半径与现场试验得到的影响半径的最大误差为8.14%,满足工程要求。
3) 当注液孔半径小于0.2 m时,随注液孔孔径增加,影响半径成非线性增加;当注液孔半径大于0.2 m时,随注液孔孔径增加,影响半径近似成线性增加,目前原地浸矿工程中的注液孔半径通常为0.1 m,此时影响半径对注液孔径的导数值大于1,具有较高的注液效率,表明孔径是合理的。
4) 当注液孔半径为0.1 m和孔中液面高度不超过3 m时,注液孔影响半径与孔中液面高度近似成线性关系。
REFERENCES
[1] 田 君, 尹敬群, 欧阳克氙, 池汝安. 风化壳淋积型稀土矿提取工艺绿色化学内涵与发展[J]. 稀土, 2006, 27(1): 70-72, 102.
Tian Jun, Yin Jing-qun, Ouyang Ke-xian, CHI Ru-an. Development progress and research connotation of green chemistry of extraction process of rare earth from weathering crust elution-deposited rare earth ores in China[J]. Chinese Rare Earths, 2006, 27(1): 70-72, 102.
[2] 袁长林. 中国南岭淋积型稀土溶浸采矿正压系统的地质分类与开采技术[J]. 稀土, 2010, 31(2): 75-79.
Yuan Chang-lin. Leaching mining positive pressure system's geological classification and corresponding mining technology of Chinese Nanling illuviation rare earth[J]. Chinese Rare Earths, 2010, 31(2): 75-79.
[3] 赖兆添, 姚渝州. 采用原地浸矿工艺的风化壳淋积型稀土矿山“三率”问题的探讨[J]. 稀土, 2010, 31(2): 86-88.
Lai Zhao-tian, Yao Yu-zhou. Discussion on extraction rate, ore -dilution rate and ore-dressing recovery inweathered crust -leaching rare earth mines with in-situ leaching mining technology[J]. Chinese Rare Earths, 2010, 31(2): 86-88.
[4] 王观石, 邓 旭, 胡世丽, 洪本根, 罗嗣海. 非达西渗流条件下的单孔注液强度计算模型[J]. 矿冶工程, 2015, 35(3): 4-8, 13.
Wang Guan-shi, Deng Xu, Hu Shi-li, HONG Ben-gen, LUO Si-hai. A calculation model for intensity of single-hole liquid injection under non-darcy flow condition[J]. Mining and Metallurgical Engineering, 2015, 35(3): 4-8, 13.
[5] 饶 睿, 李明才, 张树标, 饶运章, 钟健民. 离子型稀土原地浸矿采场滑坡特征及防控试验研究[J]. 稀土, 2016, 37(6): 26-31.
Rao Rui, Li Ming-cai, Zhang Shu-biao, RAO Yun-zhang, ZHONG Jian-min. Experimental study on landslide features and countermeasures of in situ leaching stope of ion type rare earth mines[J]. Chinese Rare Earths, 2016, 37(6): 26-31.
[6] 汤洵忠, 李茂楠, 杨 殿. 离子型稀土矿原地浸析采场滑坡及其对策[J]. 金属矿山, 2000(7): 6-8, 12.
Tang Xun-zhong, LI Mao-nan, YANG Dian. Stope slide in in-situ leaching of ionic-type rare earth ore and its countermeasures[J]. Metal Mine, 2000(7): 6-8, 12.
[7] 曾 铃, 付宏渊, 何忠明, 贺 炜, 周功科. 饱和-非饱和渗流条件下降雨对粗粒土路堤边坡稳定性的影响[J]. 中南大学学报(自然科学版), 2014, 45(10): 3614-3620.
ZENG Ling, FU Hong-yuan, HE Zhong-ming, HE Wei, ZHONG Gong-ke. Impact of rainfall on stability of granular soil embankment slope considering saturated-unsaturated seepage[J]. Journal of Central South University (Science and Technology), 2014, 45(10): 3614-3620.
[8] 雷志栋, 杨诗秀, 谢森传. 土壤水动力学[M]. 北京: 清华大学出版社, 1988.
Lei Zhi-dong, YANG Shi-xiu, XIE Sen-chuan. Soil water dynamics [M]. Beijing: Tsinghua University Press, 1988.
[9] 张 杰, 韩同春, 豆红强, 马世国. 基于分层假定入渗模型的边坡安全性分析[J]. 中南大学学报(自然科学版), 2014, 45(9): 3211-3218.
ZHANG Jie, HAN Tong-chun, DOU Hong-qiang, MA Shi-guo. Analysis slope safety based on infiltration model based on stratified assumption[J]. Journal of Central South University (Science and Technology), 2014, 45(9): 3211-3218.
[10] 尹升华, 谢芳芳. 基于Green-Ampt模型离子型稀土柱浸试验入渗水头的确定[J]. 中国有色金属学报, 2016, 26(12): 2668-2675.
YIN Sheng-hua, XIE Fang-fang. Infiltration head of ion-absorbed rare earth with column leaching experiment determined based on Green-Ampt model[J]. The Chinese Journal of Nonferrous Metals, 2016, 26(12): 2668-2675.
[11] 何 丹, 马东豪, 张锡洲, 张佳宝, 郑子成. 土壤入渗特性的空间变异规律及其变异源[J]. 水科学进展, 2013, 24(3): 340-348.
HE Dan, MA Dong-hao, ZHANG Xi-zhou, ZHANG Jia-bao, ZHENG Zi-cheng. Regularity of spatial variability of soil infiltration and its variation sources[J]. Advances in Water Science, 2013, 24(3): 340-348.
[12] 赵伟霞, 张振华, 蔡焕杰, 谢恒星. 恒定水头井入渗Green-Ampt模型的改进与验证[J]. 水利学报, 2010, 41(4): 464-470.
ZHAO Wei-xia, ZHANG Zhen-hua, CAI Huan-jie, XIE Heng-xing. Improvement and verification of the Green-Ampt model for constant-head well permeameter[J]. Journal of Hydraulic Engineering, 2010, 41(4): 464-470.
[13] 张克恭, 刘松玉. 土力学(第三版)[M]. 北京: 中国建筑工业出版社, 2010-8.
Zhang Ke-gong, Liu Song-yu. Soil mechanics(Third Edition)[M]. Beijing: China Building Industry Press, 2010-8.
[14] SCHAAP M G, FEIKE J. Improved prediction of unsaturated hydraulic conductivity with the Mualem-Van Genuchten model[J]. Soil Science Society of America, 2002, 64(3): 843-851.
[15] MEIN R G, FARRELL D A. Determination of wetting front suction in the Green-Ampt equation[J]. Soil Science Society of America Proceedings, 1974, 38(6): 872-876.
[16] 吕 特, 张 洁, 薛建峰, 黄宏伟, 于永堂. Green-Ampt模型渗透系数取值方法研究[J]. 岩土力学, 2015, 36(S1): 341-345.
Lü Te, Zhang Jie, Xue Jian-feng, HUANG Hong-wei, YU Yong-tang. Determining permeability coefficient of Green-Ampt modelfor infiltration analysis[J]. Rock and Soil Mechanics, 2015, 36(S1): 341-345.
[17] 叶为民, 钱丽鑫, 白 云, 陈 宝. 由土–水特征曲线预测上海非饱和软土渗透系数[J]. 岩土工程学报, 2005, 27(11): 1262-1265.
Ye Wei-min, Qian Li-xin, Bai Yun, CHEN Bao. Predicting coefficient of permeability from soil-water characteristic curve for Shanghai soft soil[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(11): 1262-1265.
A calculation model of influence radius of single-hole injection in in-situ leaching
GUI Yong1, WANG Guan-shi2, 3, LAI Yuan-ming2, HONG Ben-gen1, HU Shi-li3, LONG Ping1
(1. School of Resources and Environmental Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China;
2. Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences, Lanzhou 730000, China;
3. School of Architectural and Surveying & Mapping Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China)
Abstract: It is of great significance for the reasonable determination of the hole pattern parameters to master the influence radius of single-hole injection in steady state. This work assumed that the wetted body above the hole bottom was ellipsoid, based on the infiltration intensity around injecting hole equals to the leaching intensity in the influenced area of hole bottom, a calculation model was established for the influence radius of single-hole injection under steady infiltration state. The liquid height in the hole and the influence radius were obtained by field test under five kinds of injection intensity, and compared with the calculated results. The results show that the maximum error between calculated value and measured value of the influence radius is 8.14%, up to the requirement of project, so the validity of the model is proved. When the injecting hole radius is not more than 0.2 m, the influence radius increases nonlinearly with the increase of aperture. And the influence radius increases linearly with the increase of aperture when the injecting hole radius is more than 0.2 m. The influence radius of the injecting hole is approximately linear with the liquid height in the hole when the injecting hole radius is 0.1 m and the liquid height in the hole is not more than 3 m.
Key words: in-situ leaching; injecting hole; influence radius; ion-type rare earth
Foundation item: Projects(51664015, 41602311, 51264008) supported by the National Natural Science Foundation of China; Project(GJJ150658) supported by the Science and Technology Project of Education Department, China; Project(KJLD14042) supported by the Science and technology landing project of Jiangxi Provincial Education Department, China
Received date: 2017-03-06; Accepted date: 2017-05-22
Corresponding author: WANG Guan-shi; Tel: +86-13576737701; E-mail: wgsky010@ 126.com
(编辑 王 超)
基金项目:国家自然科学基金资助项目(51664015,41602311,51264008);教育厅科技项目(GJJ150658);江西省教育厅科技落地计划项目(KJLD14042)
收稿日期:2017-03-06;修订日期:2017-05-22
通信作者:王观石,教授,博士;电话:15179716062;E-mail:wgsky010@126.com