Characteristics analysis and library development forpiezoelectric transformer to drive aballast for a 35W class fluorescent lamp using PSPICEmodeling
来源期刊:中南大学学报(英文版)2016年第1期
论文作者:KIM Young-Choon
文章页码:169 - 180
Key words:PSPICE;35W-class;cold cathode fluorescent lamp (CCFL);fluorescent lamp;library
Abstract: PSPICE model driven by an electric equivalent circuit of a piezoelectric circuit is presented. In order to confirm this model to be effective, an independent model of cold cathode fluorescent lamp (CCFL) driving circuit is used to conduct simulations, leading to a precise modeling. A library is configured through modeling and its accuracy is verified through simulations for widely used and representative lamps such as CCFL, fluorescent lamps, HID lamps, and electrodeless fluorescent lamps. On the basis of experiments, a lamp simulation is also performed using PSPICE, which allows us to take advantage of the lamp library easily. Also, PSPICE model driven by an electric equivalent circuit of a piezoelectric transformer is presented. In order to confirm this model to be effective, an independent model of CCFLdriving circuit is used to conduct simulations, leading to a precise modeling. In addition, a newtype of electronic ballast is proposed, which allows 35W-class (T5-class) fluorescent lamp to work. This system is built by a rectifier which has improved power factor and half-bridge series resonant inverter. Also, with size of 27.5mm high, 27.5mm wide and 2.5mm thick, the produced piezoelectric transformer has a high step-up ratio, through which it is possible for the electric ballast circuit to be lighter, smaller and more efficient. After the produced ballast is used to drive the fluorescent lamp for 25 min, it yields0.95 in power factor correction, 86% in efficiency, 35.07W in output voltage and 20.5°C in temperature increase while meeting the characteristics of the 35W-class fluorescent lamp.
J. Cent. South Univ. (2016) 23: 169-180
DOI: 10.1007/s11771-016-3060-x
KIM Young-Choon
Division of Mechanical and Automotive Engineering College of Engineering,
Kongju National University, Chungnam 330-717, Korea
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: PSPICE model driven by an electric equivalent circuit of a piezoelectric circuit is presented. In order to confirm this model to be effective, an independent model of cold cathode fluorescent lamp (CCFL) driving circuit is used to conduct simulations, leading to a precise modeling. A library is configured through modeling and its accuracy is verified through simulations for widely used and representative lamps such as CCFL, fluorescent lamps, HID lamps, and electrodeless fluorescent lamps. On the basis of experiments, a lamp simulation is also performed using PSPICE, which allows us to take advantage of the lamp library easily. Also, PSPICE model driven by an electric equivalent circuit of a piezoelectric transformer is presented. In order to confirm this model to be effective, an independent model of CCFL driving circuit is used to conduct simulations, leading to a precise modeling. In addition, a new type of electronic ballast is proposed, which allows 35 W-class (T5-class) fluorescent lamp to work. This system is built by a rectifier which has improved power factor and half-bridge series resonant inverter. Also, with size of 27.5 mm high, 27.5 mm wide and 2.5 mm thick, the produced piezoelectric transformer has a high step-up ratio, through which it is possible for the electric ballast circuit to be lighter, smaller and more efficient. After the produced ballast is used to drive the fluorescent lamp for 25 min, it yields 0.95 in power factor correction, 86% in efficiency, 35.07 W in output voltage and 20.5 °C in temperature increase while meeting the characteristics of the 35 W-class fluorescent lamp.
Key words: PSPICE; 35 W-class; cold cathode fluorescent lamp (CCFL); fluorescent lamp; library
1 Introduction
In the 1960s, a piezoelectric transformer was developed as a high-tension transformer, but such development was stopped due to difficulty involved in attaining attributes of high tension. However, it was 1994 when NEC began to develop piezoelectric transformers that adopted the symmetrical Rosen third method, used in back-light inverters of laptop LCD screens. Since then, there have been many studies on this issue [1–3].
The piezoelectric transformer is optimal for driving fluorescent lamp because its transformation ratio is changeable to load conditions. In this case, almost all of the output waveforms appear to be a type of sine wave regardless of input waveform. Since the property of piezoelectric transformer is much similar to lighting of a fluorescent lamp, the transformer can drive the fluorescent lamp by using voltage and current similar to sine wave. Nevertheless, if resonance frequency that the transformer can drive is not precisely provided, the transformer will become useless [4–6].
Since Thomas Edison invented the light bulb in 1879, lamps in various forms and of various performances have been developed. In the modern world, the common lamp is one of the most important and indispensable items and is used in various fields in addition to simple lighting.
However, the development and the application of various circuits using lamps require simulations that are currently performed with an alternative and simplified model, which is essentially a serial connection of loads such as resistors and inductors. Such an alternative simulation methodology can provide rough characteristics but has clear limitation in accurately verifying the functionality. If more detailed and precise lamp modeling is available, an accurate circuit analysis using lamps can be carried out accordingly. However, most simulation tools including PSPICE do not provide a lamp library. Therefore, in practice, most users perform complex modeling tasks or simply use a resistor-inductor series load as an alternative [7–10].
To address such challenges, in this work, we model widely used lamps and build a library. We use PSPICE, a general-purpose and easy-to-use simulation tool. We model a CCFL, a fluorescent lamp, HID lamps, and electrodeless fluorescent lamps, which are popular recently and now used widely, and apply them to our simulation setup, which leads to good functional characteristics as a result. With the output from this study, we expect that a user can obtain more accurate lamp simulation results with considerably less effort [11-13].
In addition, this research work aims to develop a high-efficient ballast of a fluorescent lamp that is absolutely necessary to replace an existing fluorescent lamp, highly important as a lighting load, with the next generation one, super-efficient T5 fluorescent lamp of 35 W. To this end, the effort is made to apply the circuit that can improve power factor to the ballast, and adapt the piezoelectric transformer to an inverter of the ballast. For the piezoelectric transformer, if frequency is provided by using only voltage controlled oscillator (VCO), there can be some changes in frequency that can be easily provided in accordance with surrounding environment, such as physical change. In order to address this issue, phase locked loop (PLL) is adapted to compare a phase between output and feedback frequencies, and to lock up that phase in order to provide a precise resonance frequency to the piezoelectric transformer.
2 Modeling of piezoelectric transformer
2.1 AC equivalent circuit
VLr(t), the voltage from input of the piezoelectric transformer can be demonstrated as
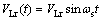 (1)
(1)
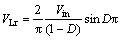 (2)
(2)
The equivalent impedance from output of the piezoelectric transformer can be displayed as
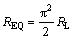 (3)
(3)
To precisely show a property of efficient frequency, the extrinsic resistance, rcd1 and Cd1, in the equivalent circuit of Fig. 1, are input, and RLS and Rd are the equivalent resistance of Ls.
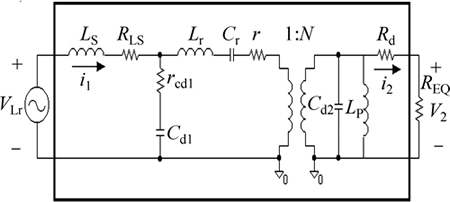
Fig. 1 AC equivalent circuit of piezoelectric converter
The average value of output voltage, V0, drawn during half cycle, can be demonstrated in Eq. (4) and G, step-up ratio, in Eq. (5):
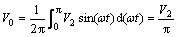 (4)
(4)
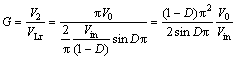 (5)
(5)
Relations between input (output) voltage and current can be measured in Eq. (6) that is interpreted as F-matrix, as shown in Fig. 2. In this case, elements of F-matrix can be demonstrated in Eq. (7):
 (6)
(6)
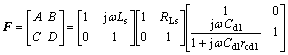 .
.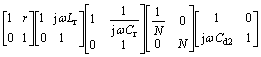 .
.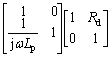 (7)
(7)
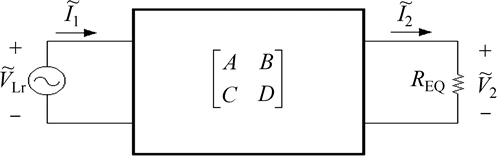
Fig. 2 F-matrix
The step-up ratio, G, of the AC equivalent circuit can be interpreted in Eq. (8) and V0, output voltage, can be measured in Eq. (9) by using Eqs. (4) and (8):
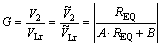 (8)
(8)
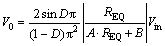 (9)
(9)
Input power, Pin, output power, P0, and efficiency, η, can be demonstrated in Eqs. (10), (11) and (12), respectively:
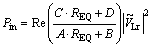 (10)
(10)
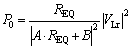 (11)
(11)
 (12)
(12)
Figure 3 shows the equivalent circuit of the piezoelectric transformer, and PSPICE-based library is established on the basis of this circuit.
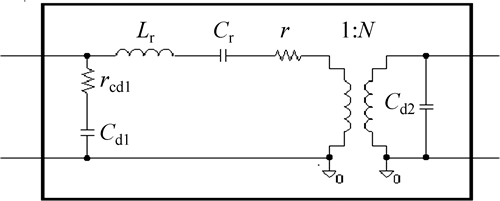
Fig. 3 Equivalent circuit of piezoelectric transformer
2.2 Application of piezoelectric transformer to electronic ballast
This work attempts to find the appropriate driving voltage and frequency of the piezoelectric transformer in a bid to figure out the result after applying them to the electronic ballast. The circuit of entire ballast consists of power, control and driving circuits, and Fig. 4 shows a block diagram of the electronic ballast.
L6561, produced by ST, is used as power factor correction (PFC) integrated circuit (IC). PLL IC 14046B is the control system that locks up the specific phase by comparing reference frequency with input signal, and it is used to tie up the frequency as its source. By doing so, the frequency can be prevented from shaking. Although the electronic ballast produces the frequency source through VCO, output frequency is vulnerable to surrounding environment to a great extent. The output frequency can be subtly shaken by influence of circuits, peripheral devices, temperature and climate, all of which make the frequency change to different ones. When the piezoelectric transformer, driven in a specific frequency, is applied to the electronic ballast, it is possibly operated in bandwidth of 2–3 kHz, but bandwidth, driven with an appropriate step-up ratio, can be narrower. Therefore, in this system, PLL plays a role in keeping the frequency source from shaking and correctly changing it.
Figure 5 shows a push–pull inverter, including an equivalent circuit of the piezoelectric transformer, and in this case, PSPICE model is shown in Fig. 6. In this circuit, CCFL is interpreted as resistance of 100 kΩ, RL, and Fig. 7 demonstrates simulation waveform of several factors: Q1, Q2 gates; drain voltage; current of L1, L2; and input (output) voltage from the piezoelectric transformer. In addition, Fig. 8 shows waveform that is drawn when load resistance changes to 200, 150, 100 and 50 kΩ, while Fig. 9 indicates output voltage of the piezoelectric transformer according to driving frequency. Figure 10 shows waveform drawn by the simulation during which inductance, L1 and L2, change to 50, 100 and 150 μH.
3 Characteristics of lamps and modeling
3.1 CCFL modeling
A cold cathode fluorescent lamp (CCFL) is suitable for miniaturization because of its simple structure. By changing the fluorescent material type and mixture ratio, we can obtain an arbitrary fluorescent color. Further, the CCFL has longer lifetime expectancy than a hot cathode fluorescent lamp and requires only a simple lighting circuit. Further, the CCFL shows a negative resistance characteristic, requires a ballaster to limit the negative current, and has resistor-like characteristics under a stable condition.
Basically, the CCFL has four important parameters: firing potential for lighting, sustained voltage, frequency, and pipe current. The brightness of the CCFL depends not on the operating frequency but on the lamp current.
The effective voltage and current characteristics of the CCFL in this work have negative impedance at the sensitization level, and a lamp can represent two sensitization characteristics, as expressed in Eq. (13):
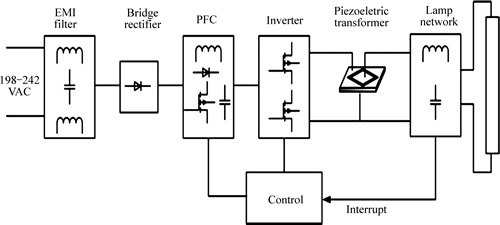
Fig. 4 Block diagram of electronic ballast
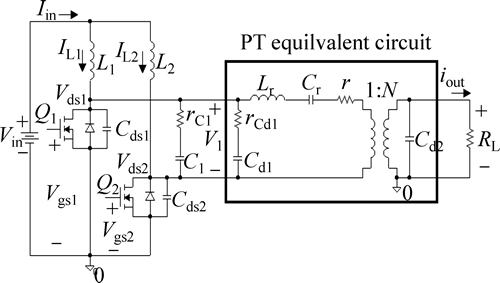
Fig. 5 Push–pull invertor using piezoelectric transformer
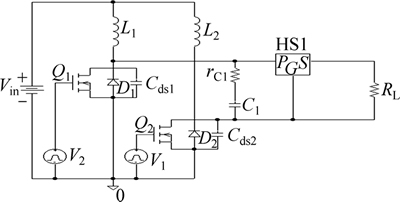
Fig. 6 Push–pull inverter PSPICE model using piezoelectric transformer
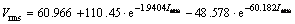 (13)
(13)
where the first term denotes the default value of the voltage–current curve, the second term shows thenegative impedance nature, and the last term indicates the positive impedance nature.
The parameters specified in Eq. (13) can be derived by computing the least square root and the equivalent impedance to a resistor-like lamp at high frequency, expressed as
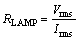 (14)
(14)
From Eqs. (13) and (14), we can express the equivalent impedance as
 (15)
(15)
From the above, we can compute the momentary voltage of a lamp Vt by using the momentary current of a lamp It:
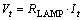
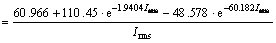 (16)
(16)
On the basis of Eq. (16), we modeled the CCFL. The momentary voltage of a lamp Vt can be described as a function of the momentary current It and the effective
current Irms. The effective value of the lamp current in a PSPICE model can be computed using an RC integration circuit, where the current source Is is defined as the square of the momentary current of a lamp It, and the output voltage VA can be obtained by integrating over the period T:
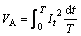 (17)
(17)
Therefore, the square root of VA is the effective value of the current It. By using such an RC integration circuit to compute the effective current of a lamp, the lamp model in Eq. (16) can be transformed into the PSPICE model in Fig. 11. H1 in Fig. 11 is a current-controlled voltage source with gain of 1, which detects the momentary current of a lamp. G1 is a voltage-controlled current source; E2 is a voltage- controlled current source with the same lamp impedance as given in Eq. (15), and E1 is a voltage-controlled voltage source with gain of 1, which generates the momentary voltage of a lamp. Figure 12 depicts the voltage and current characteristics of the CCFL.
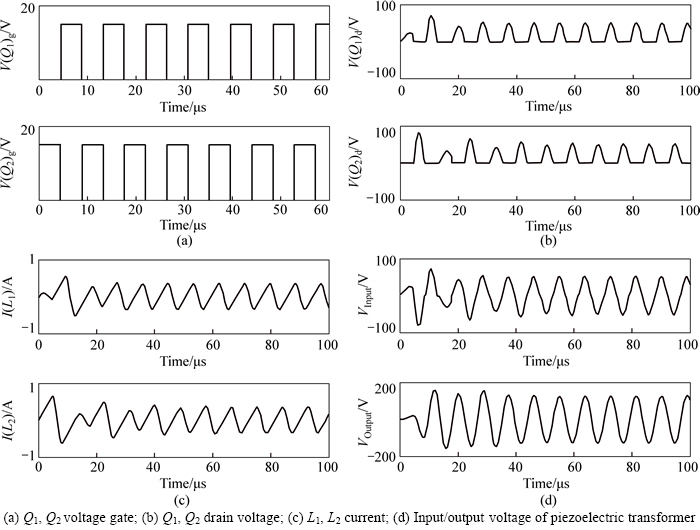
Fig. 7 Simulated waveform of push–pull inverter:
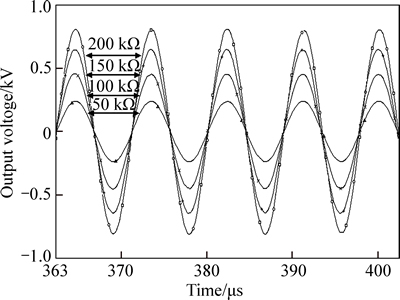
Fig. 8 Waveform of output voltage upon load resistance changing

Fig. 9 Output voltage of piezoelectric transformer according to driving frequency
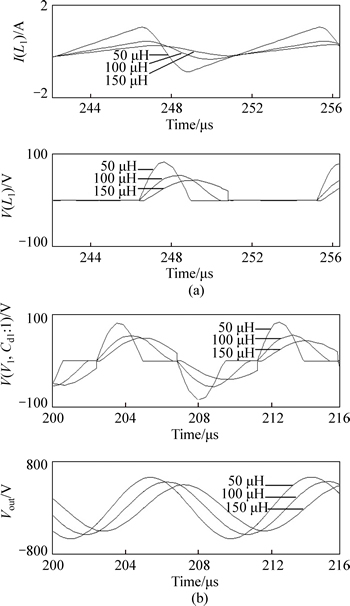
Fig. 10 Simulated waveform upon inductance L1 (a), L2 (b) changing

Fig. 11 PSPICE model for CCFL
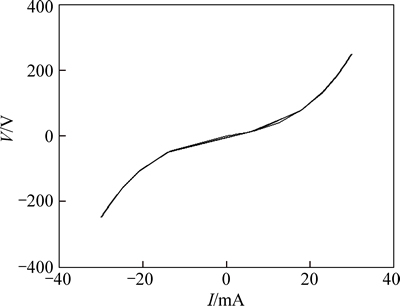
Fig. 12 V–I characteristics curve for CCFL
3.2 Fluorescent light modeling
As a type of a low-pressure gas discharge lamp, fluorescent light can be best described by the flow of current through the carrier gas. Gas discharge or arc plasma occurs in a lamp tube. The discharge length consists of several regions between the positive column and the anode drop, which play an important role in the overall lamp behavior. Therefore, we model fluorescent light by focusing mainly on these two regions.
The Cassie equation where conductance G is a dependent variable is expressed in Eq. (18), which describes the arc behavior in the case of a high current:
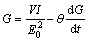 (18)
(18)
where E0 is the arc voltage, θ is the arc time ratio, V is the lamp voltage, and I is the lamp current.
The Mayr equation is given as Eq. (19); it describes the arc behavior in the case of a low current:
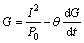 (19)
(19)
where P0 is the power loss.
The Mayr and Cassie equations are effective in the cases of 0 or low current and high voltage ranges, respectively. The positive column can be simulated using Eqs. (18) and (19). The conductance in the anode drop is proportional to conductance G0 in the positive column, and inversely proportional to the linear function of the lamp current I. The relationships among these models are described by
 (20)
(20)
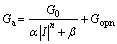 (21)
(21)
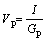 (22)
(22)
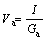 (23)
(23)
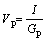 (24)
(24)
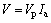 (25)
(25)
where Gp and Ga are the conductances of the positive column and the anode drop, respectively; Vp and Va are the voltage drops in the positive column and the anode drop, respectively; Gopn is the conductance of the anode drop.
The arc model for fluorescent light is built using PSPICE. Note that the PSPICE software library has numerically useful functions for circuit design and device modeling. Further, analog behavior modeling (ABM) can express mathematical relations for modeling, and a symbol library has various ABM components including an integrator, a differentiator, and a filter in the “Control System”. Using these features, we can model fluorescent light in PSPICE using Eqs.(18)–(25), as shown in Fig. 13.
Figure 14 shows the anode voltage and the lamp current of a fluorescent light, and Fig. 15 shows the lamp voltage and current characteristics curve.
3.3 HID lamp modeling
Our PSPICE model for a high-intensity discharge lamp (HID) can be built using physical properties, lamp parameters, and universal constants.
The lamp model shown in Fig. 13 and 14 can be defined as
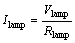 (26)
(26)
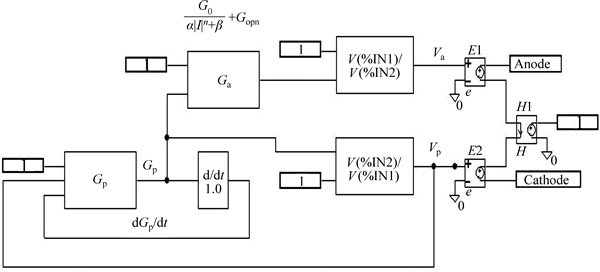
Fig. 13 PSPICE model for fluorescent light
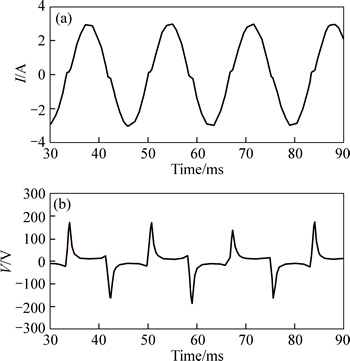
Fig. 14 Lamp current (a) and anode voltage (b) at 60 Hz
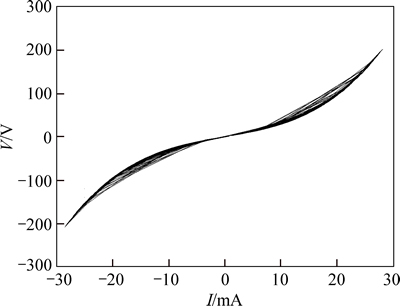
Fig. 15 Lamp voltage and current curves
where Vlamp is the voltage of the lamp;  is a nonlinear resistor in the lamp, σΣ is the universally defined plasma conductance, v is the volume of the plasma, L is the length of the plasma, and S is the cross-sectional area.
is a nonlinear resistor in the lamp, σΣ is the universally defined plasma conductance, v is the volume of the plasma, L is the length of the plasma, and S is the cross-sectional area.
Further, the universally defined conductance is in general equal to the sum of the total conductance of the plasma gas composition:
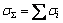 (27)
(27)
The conductance for weakly ionized plasma, σi, is a function of temperature and can be expressed by
 (28)
(28)
where σ0i is a gas composition constant, T is the temperature, ρ is the gas pressure, and Ei is the ionized energy of the i, k component in Boltzmann’s constant.
The increase amount in arc heating dQ can be described as follows:
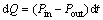 (29)
(29)
where Pin is the input power to a lamp, Pout is the output power from the lamp, and dt is the time difference.
Equation (29) can be transformed into Eq. (30), which describes the heat increase in the arc per unit length on the basis of the assumption given in Ref. [9]:
 (30)
(30)
where carc and cper are the heating capacities of the inner and outer layers, respectively; ρarc and ρper are the densities of the inner and outer layers, respectively; Rtube and Rel are the radii of an arc hole and electrode, respectively; KT,red is the temperature reduction factor in the arc exterior.
The input power per unit length in the lamp, Pind, is expressed by
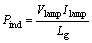 (31)
(31)
where Lg is the distance between the electrodes.
The radiant energy, Prad, can be expressed as
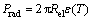 (32)
(32)
where ε(T) is the emissivity on the arc surface.
The heat conduction loss, Pcon, can be given as
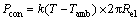 (33)
(33)
where k=k(T) is the heat transfer coefficient.
After applying Eqs. (20)–(33) to Eq. (29), we can obtain the differential equation:
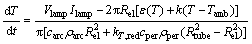 (34)
(34)
Once we mathematically describe Eq. (25) in PSPICE, we can build the HID lamp model shown in Fig. 16. Figures 17 and 18 respectively show the waveforms of the HID lamp obtained from our PSPICE simulation model at 60 Hz and 30 kHz, respectively.
3.4 Electrodeless fluorescent modeling
Lamp impedance can be viewed as resistance when operating at high frequency, and the effective voltage and current values as well as the lamp impendence at all operating points can be defined by using Ohm’s law:
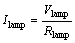 (35)
(35)
where Ilamp is the lamp current, Vlamp is the lamp voltage, and Rlamp is the lamp impedance.
The relation between impedance and current can be defined as
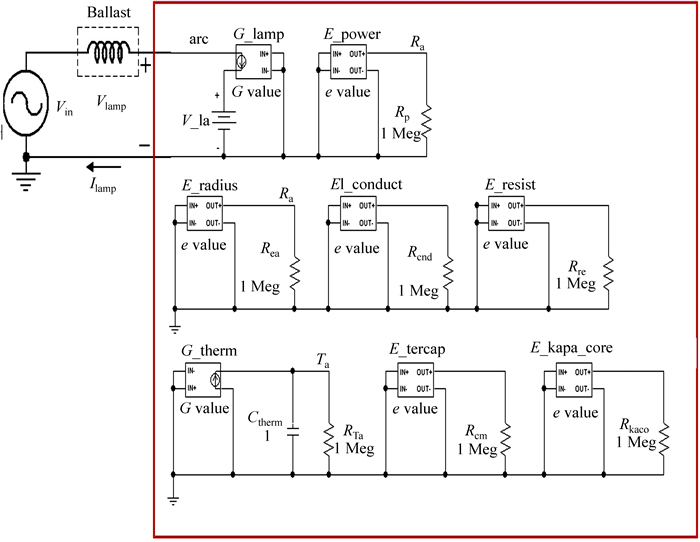
Fig. 16 PSPICE model for HID lamp
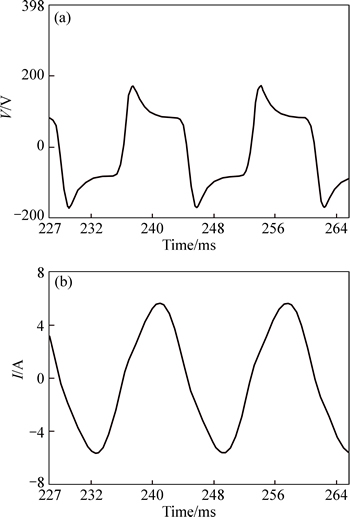
Fig. 17 Voltage (a) and current (b) curves for HID lamp at 60 Hz
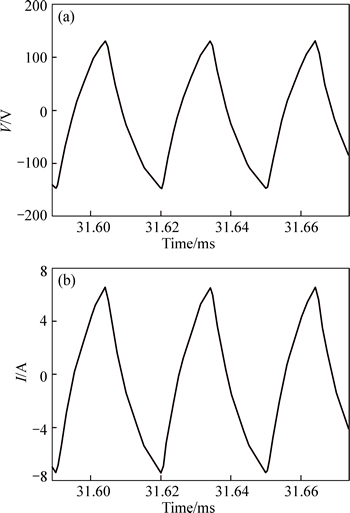
Fig. 18 Voltage (a) and current (b) curves for HID lamp at 30 kHz
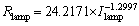 (36)
(36)
In this work, the circuit model by Ben-Yaakovis is used, and the lamp is viewed as the dependent current source G1 for computing the impedance by using Eq. (36). The output of the dependent voltage source E1 is proportional to the square root of the voltage on capacitor C1, which is described in Eqs. (37)–(40):
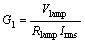 (37)
(37)
 (38)
(38)
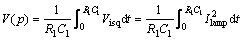 (39)
(39)
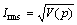 (40)
(40)
Figure 19 shows PSPICE model of electrodeless lamp, as expressed by Eqs. (37)–(38). Figure 20 shows a test circuit for the electrodeless lamp, and Fig. 21 shows the voltage and current forms of the lamp.
4 Experiment result
The produced circuit was used to drive the piezoelectric transformer through around 79 kHz driving frequency, and Fig. 22 shows waveform between drain sources of two MOSFET which was measured when it was stabilized after the fluorescent lamp was turned on. In order to prevent two switches from being turned on simultaneously, an appropriate dead time (0.1 μs) was given.
Figure 23(a) shows the voltage that was input to the entire ballast when the T5 fluorescent lamp was turned on while waveform in Fig. 23(b) indicates output of the ballast with input power of 40.59 W, output power of 35.07 W and 86% in efficiency of the entire ballast. Total efficiency in piezoelectric transformer was measured to be 87%.

Fig. 19 PSPICE model for electrodeless lamp
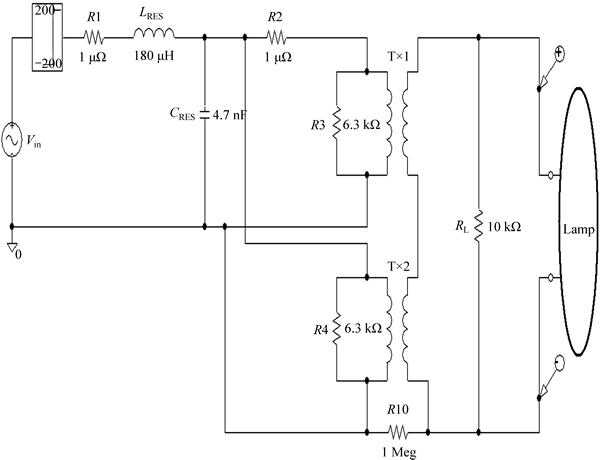
Fig. 20 Test circuit for electrodeless lamp
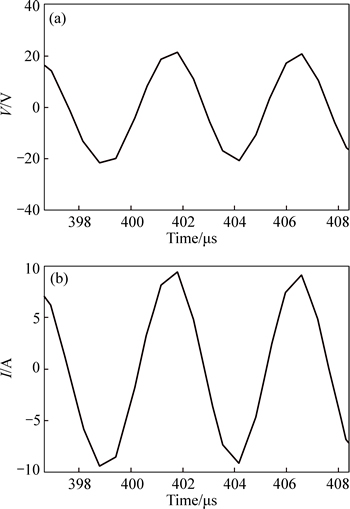
Fig. 21 Voltage (a) and current (b) curves for electrodeless lamp
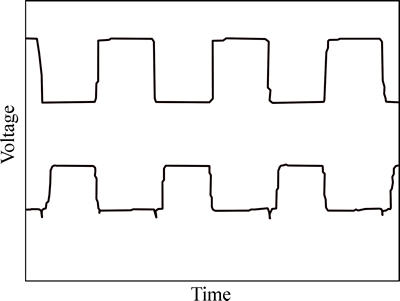
Fig. 22 Delayed-time waveform of half bridge inverter
Figures 24(a) and (b) show input and output voltage waveforms drawn before and after the light was turned on, respectively. Figure 24 indicates that the phase before light on almost reaches 0° while locked at 50° after light on due to PLL acting. Figure 25 shows the produced electronic ballast attached with a ring-dot type piezoelectric transformer while Fig. 26 demonstrates time and voltage-current waveforms taken from early discharge to lighting. Considering that T5 fluorescent lamp has small diameter, there is enough preheating time (about 1 s), leading to less stress on electrodes of the lamp.
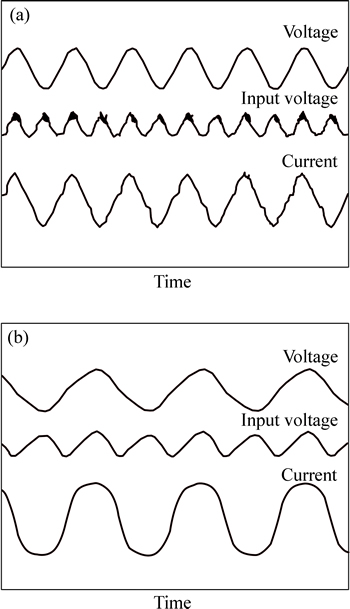
Fig. 23 Input (a) and Output (b) characteristics of ballast
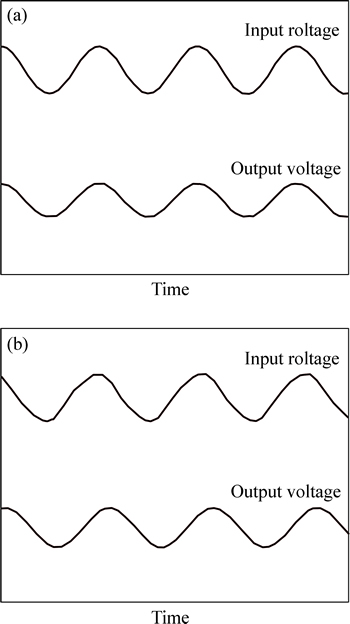
Fig. 24 Input and output characteristics of piezoelectric transformer before (a) and after (b) turning on of lamp

Fig. 25 Picture of produced electronic ballast
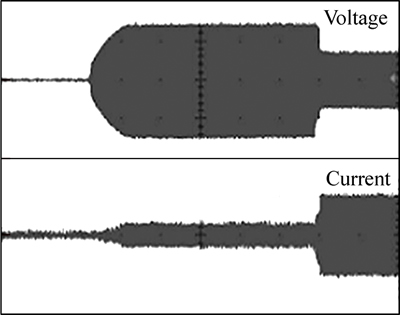
Fig. 26 Lighting characteristics of lamp
Figure 27 shows, in room temperature (the piezoelectric transformer’s ambient temperature stood at around 20 °C measured by a non-contact thermometer), curves that were measured for rise in temperature of the piezoelectric transformer in every 2 min for 0.5 h after the lamp was turned on. As shown in Fig. 27, it is found that the curve of temperature remained flattened after around 20 min passed. Figure 28 demonstrates an appearance of 35 W (T5) fluorescent lamp after light was turned on.

Fig. 27 Up-curve of temperature in piezoelectric transformer based on driving time

Fig. 28 Picture of electronic ballast driving
5 Conclusions
The modeling of the piezoelectric transformer was done by using equivalent circuit. By doing so, load resistance was changed, and output voltage was drawn based on driving frequency. In addition, the property of resonance, subjected to load condition and input current, was found after the simulation was conducted to define input and output characteristics of the piezoelectric transformer, both of which were drawn when inductance of input was changed. The produced piezoelectric transformer was used to drive the T5 fluorescent lamp.
1) The power ratio (step-up ratio) to the input of the piezoelectric transformer near resonance point reaches the highest with unloading, and it is turned into an appropriate value in the normal condition, showing the characteristics of the fluorescent lamp.
2) With size of 27.5 mm high, 27.5 mm wide and 2.5 mm thick, the produced piezoelectric transformer has a high step-up ratio, through which it is possible for the electric ballast circuit to be lighter, smaller and more efficient.
3) With the PLL system adapted, frequency for input of the piezoelectric transformer is locked up while output phase to input is locked up, leading to phase difference tied up at around 50°, which, in turn, increases the efficiency of the transformer.
4) After the produced ballast is used to drive the fluorescent lamp for 25 min, it yields 0.95 in power factor correction, 86% in efficiency, 35.07 W in output voltage and 20.5 °C in temperature increase while meeting the characteristics of the 35 W (T5) fluorescent lamp with rated 210 V and 170 mA in the normal condition.
References
[1] PETER L, DONG B L, ATLURI S N. Multi-physic computational grain (MPCGs) for direct numerical simulation (DNS) of piezoelectric composite/porous materials and structure [J]. Computational Mechanics, 2014, 54(5): 1129–1139.
[2] ZENQ Ping, CHEN Yan-hui, GAO Yin-ying, LI Yan-peng, CHENG Guang-ming. Simulation analysis and experimental research on circular piezoelectric bone-conduction headphone [J]. Advanced Materials Research, 2014, 1030–1032: 2313–2319.
[3] JIANG Bing, YUAN Shuai, XIN Jian-bo, CHEN Li-juan, HAO Yu-guo, ZHANG Hua-qing. Modeling and simulation of bow-shaped piezoelectric energy harvester [J]. Advanced Materials Research, 2014, 1033–1034: 1338–1343.
[4] XIE Xin, FAN S X, FAN D P, LIU H. A piezo/gear compound drive: Principles analysis and simulation [J]. Key Engineering Materials, 2014, 621: 346–360.
[5] ZHENG Wei, LIN B S, DONG J S, SHI J Y, WU B D. Theoretical analysis and experimental study on the vibration of the bimorph piezoelectric vibrator for piezoelectric pump [J]. Applied Mechanics and Materials, 2014, 551: 164–169.
[6] PAN Wei, LU C H, LIU Z C. Design of energy-saving peizoelectric actuator drive for high frequency servo valve [J]. Applied Mechanics and Materials, 2014, 651–653: 957–961.
[7] HWANG L H, YOO J H, HAN Xiao, YU Ming-zhi, KIM H S, OH H S, CHO M T, CHO G S. A study on the modeling of piezoelectric transformer for CCFL using a PSPICE [C]// ICPE '07. 7th International Conference. Daegu, Korea, 2007: 122–126.
[8] HWANG L H, YOO J H, LEE B H, JANG E S, CHO M T. Modeling of piezoelectric transformer and CCFL by PSPICE [C]// PowerCon 2002. Kunming, China, 2002: 2664–2668.
[9] HWANG L H, YOO J H, LEE B H, KIM J R, JANG E S, CHO M T. MATLAB and PSPICE micro-modeling of piezoelectric transformer for CCFL drive [C]// Proceedings of the 13th IEEE International Symposium. Nara, Japan, 2002: 281–285.
[10] HWANG L H, YOO J H, SONG H S, NA S K, KIM H S, OH H S, LEE S H, CHOI K H, CHO M T. A study on driving of 35 W (T5) fluorescent lamp by the electronic ballast using piezoelectric transformer [C]// Power Electronics, 2007. ICPE '07. 7th International Conference. Daegu, Kouea, 2007: 221–224.
[11] HWANG L H, YOO J H, KIM J R, JANG E S, LEE C S, CHO M T, KIM J S. A study on the T5 fluorescent lamp ballast used contour vibration mode piezoelectric transformer using a one-chip microcontroller [C]// Proceedings of the 13th IEEE International Symposium. Nara, Japan, 2002: 287–290.
[12] HWANG L H, YOO J H, JANG E, OH D, JEONG Y, AHN I, CHO M T. Fabrication and characteristics of PDA LCD backlight driving circuits using piezoelectric transformer [J]. Sens Actu, 2004, 115: 73–78.
[13] JEONG H S, CHOI B C, YOO J H, IM I H, PARK C Y. Parallel driving of piezoelectric transformer [J]. Jpn J Appl Phys, 1999, 38(9A): 5166–5169.
(Edited by YANG Bing)
Received date: 2015-03-10; Accepted date: 2015-08-08
Corresponding author: KIM Young-Choon, Professor, PhD; Tel: +82-11-9550-0374; E-mail: yckim59@kongju.ac.kr

