DOI:10.19476/j.ysxb.1004.0609.2018.03.18
金属薄壁管件外压缩径成形理论及实验研究
杜 冰,谢 军,关风龙,张 鑫,赵长财
(燕山大学 先进锻压成形技术与科学教育部重点实验室,秦皇岛 066004)
摘 要:起皱失稳问题是空心薄壁类零件在加工和应用领域的主要瓶颈。基于此,对金属薄壁管件缩径成形过程中的弹塑性失稳规律进行研究,提出预测缩径褶皱、提高成形件质量的方法及技术手段。基于L. H. Donnell线性屈曲理论,推导了管坯均布外压作用下的环向弹性及塑性起皱临界载荷表达式;探讨了成形条件及材料参数对管材抗起皱性能强弱的影响。利用固体颗粒介质缩径工艺实现了AA7075管材不同热处理条件下的缩径成形,工艺试验验证了管材缩径成形起皱失稳理论的相关结论。
关键词:AA7075铝合金管件; 缩径成形; 起皱失稳; 固体颗粒介质成形
文章编号:1004-0609(2018)-03-0586-08 中图分类号:TG386.43 文献标志码:A
空心薄壁构件由于其轻量化、强韧化及高精度的特征优势,已被交通运输、航空航天等技术领域广泛采纳,越来越多的新材料、新工艺和新结构的空心薄壁构件不断涌现,各国工业领域都投入了大量资金来研发其相关的成形技术。其中,缩径管是结构上具有代表性的典型空心薄壁构件之一,应用场合广泛。但是由于缩径管成形过程中的起皱失稳问题,使其在工程领域的应用和制造受到了很大程度的制约。
薄壁件成形过程中的起皱失稳是由于其厚度远小于其他方向尺寸,当板壳面内某方形受到的压应力达到某临界压应力数值时,发生的变形由面内转移到面外导致皱纹出现。随着近年来破裂失稳问题研究的趋于完备,较之更为复杂的起皱失稳问题逐步跃升为金属成形领域的研究热点问题,国内外学者从多角度进行了研究。WANG 等[1]采用平面和曲面两种压边圈来研究压边圈类型对5182-O铝合金板材室温拉伸性能的影响,结果表明:板材在曲面压边圈的作用下,在不同方向的流动更加均匀,从而能更大程度地阻止法兰起皱问题。ABBAS等[2]通过数值模拟建立了径向压力辅助充液拉深工艺下3种材料钢板的工艺窗口图,通过该图可快速评估成形零件的可制造性—预测不同加载路径下合适的加工区间以及会发生破裂、起皱缺陷的可能性;JU等[3]利用HILL[4]于1958年提出的分叉理论对管纯弯情况下的起皱进行了预测,预测结果与试验结果吻合较好。ZHOU 等[5]等通过试验和仿真研究车门防撞梁生产中经常出现的减薄、破裂、起皱和回弹等缺陷,进行冲压试验和模拟弄清了成形缺陷的量化规律并分析了工艺参数对成形缺陷的影响。汤泽军等[6]对管材液压胀形时的轴向塑性起皱临界载荷进行了分析,建立了管材内高压成形轴向起皱临界应力的解析表达式,提出起皱临界载荷是管材进入塑性阶段时的屈服载荷与塑性起皱载荷之和。SUN 等[7]基于ABAQUS/Explicit对Ti-15-3钛合金室温锥杯成形实验中悬空侧壁起皱现象进行分析,通过对零件边缘的皱纹波长和峰高的定量研究,获取较适合Ti-15-3钛合金室温成形侧壁起皱的模拟参数。将 Ti-15-3钛合金室温锥杯成形起皱获取的模拟参数,用于Ti-15-3钛合金凸弯边橡皮成形起皱的预测,经实验验证,有限元模拟对Ti-15-3钛合金凸弯边上皱纹的模拟与实验结果有很好的一致性。
管材外压缩径成形工艺不同于常规的薄壁件成形工艺-管材板面内环向方向始终受到压应力的作用,成形区极易进入失稳状态,顺利缩径难度较大,工程应用受此限制从而影响到学术界对于缩径工艺鲜有研究。为此,结合颗粒介质管材内高压工艺实施便捷的优势,开展管材缩径成形工艺的研究。本文作者基于弹性失稳和塑性成形理论,对缩径失稳规律进行研究,采用固体颗粒介质成形工艺试制了AA7075铝合金缩径管件,以探求缩径成形的规律及工艺特点。
1 管材外压缩径理论分析
1.1 管材外压起皱失稳临界力分析
美国学者Von Karman是研究结构塑性失稳方面的先驱,他通过实验证实了塑性稳定问题可以利用弹性稳定公式做近似的分析。因为在弹性失稳问题中,稳定方程除几何尺寸外,在材料力学性能方面仅涉及弹性模量E,在塑性范围内的失稳只要利用卡曼缩减模数Et代替E,弹性稳定理论就可以运用于塑性失稳中[8]。但是,KARMAN等[9]和TSIEN[10]提出并证实了由于薄壳存在物理和几何方面的初始缺陷(如焊缝、尺寸偏差和残余应力等),导致失稳分析结果与实际差别较大。为此,考虑各种特殊情况下的薄壳失稳理论与分析方法陆续被建立[11-14],但由于失稳模型多为超越方程或非线性方程组,需要借助多次迭代求解,无法给出临界失稳压力的解析表达式,不适合工程应用中起皱规律的探讨研究。本文作者为探求管材材料性能和成形几何条件等主要参数对缩径成形过程中弹塑性失稳的影响规律,忽略管材初始缺陷的影响。
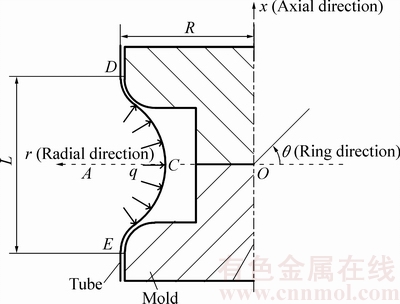
图1 管坯外压缩径原理图
Fig. 1 Schematic diagram of tube outer pressure compression forming
1.1.1 弹性起皱失稳分析
管坯外压缩径原理如图1所示。选用柱坐标系分析缩径过程中的起皱失稳现象。图1中,x为变形区轴向坐标;r为径向坐标;θ为环向坐标。缩径过程中管坯成形区体积被压缩,设ω、u、v分别为筒壁中性层任意点径向、轴向、环向的位移,假设管坯任一截面环向屈曲形态满足余弦波分布,则位移表达式为
 (1)
(1)
式中:n为环向波数。为了使求解未知参量的方程组解正定且能够得到解析解,从而方便缩径起皱失稳规律的分析,需假设管坯服从固支边界条件(图1中D、E位置无位移),即当 时,有
时,有
 (2)
(2)
通过位移形式的圆柱壳唐纳(L.H.Donnell)线性屈曲方程组(3)对假设管端固支、管外受均布外压条件下的弹性临界失稳外压qcr进行求解:
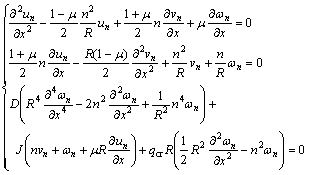 (3)
(3)
式中:μ为泊松比;R为管坯中性层半径。索贝尔(L.H.Sobel)给出了方程组(3)的通解形式[15]:
 (4)
(4)

式中:ri是下面特征方程的4个根。


式中:δ为管材壁厚;E为弹性模量;L为缩径区长度。
将固支边界条件式(2)代入方程组(4)中,即可得到关于Ai、Bi的8个线性齐次代数方程组。令方程组的系数行列式为零,可得管坯临界失稳外压与材料性能参数、成形几何条件之间的关系式,可写为
 (5)
(5)
式中:Z定义为Bathorf参数, ;
; 和kp为与周向波数n和与弹性临界失稳外压qcr有关的参量,表达式分别为
和kp为与周向波数n和与弹性临界失稳外压qcr有关的参量,表达式分别为
 (6)
(6)
 (7)
(7)
式中: ,为壳的抗弯刚度。通过数值方法能够绘制出
,为壳的抗弯刚度。通过数值方法能够绘制出 ,
, 与Z的关系曲线(见图2),分别反映了临界载荷和屈曲波数与管坯几何尺寸、材料性能参数之间的关系。为了表征规律的宏观特征,采用双对数坐标系作图。
与Z的关系曲线(见图2),分别反映了临界载荷和屈曲波数与管坯几何尺寸、材料性能参数之间的关系。为了表征规律的宏观特征,采用双对数坐标系作图。

图2 参量kp和β曲线
Fig. 2 Curves of parameters kp and β with Z
图2表明,当Z≥10,即L≥ 时,β和kp可拟合为关于Z的幂指函数形式,如式(8)和式(9)所示:
时,β和kp可拟合为关于Z的幂指函数形式,如式(8)和式(9)所示:
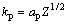 (8)
(8)
 (9)
(9)
式中:ap和bp分别为对应幂指函数的系数,且此时ap和bp均为常值,ap≈1.51,bp≈0.96。
若将图2中数值曲线的横纵坐标同时取对数,可得图3。

图3 lnkp和lnβ的数值解及其拟合曲线
Fig. 3 Numerical solution for lnkp and lnβ and their fitting curves
当Z≤10,即L≤ (图3中lnZ≤2.3)时,有
(图3中lnZ≤2.3)时,有 ,
, 。
。
将式(8)代入式(6),式(9)代入式(7),最终得到了弹性临界失稳外压qcr与失稳波数n的计算式(μ=0.3)
 (10)
(10)
 (11)
(11)
为了使上式适用于Bathorf参数Z的全局值域,规定当Z≤10时,同样存在ap和bp,为了满足此时β和kp的取值,应有 ,
,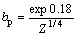 。
。
1.1.2 塑性起皱失稳分析

图4 微元C受力情况
Fig. 4 Stress state of micro unit C
式(10)仅适用于弹性范围,即qcr≤qs时。qs为管坯初始屈服外压。由于初始屈服时,管坯尚未产生塑性变形,通过图1点中C所在截面环向方向的平衡方程,可认为
 (12)
(12)
式中:σθ-s为管坯初始屈服时环向方向的应力分量;ks为屈服应力分量比。
当qcr>qs时,管坯发生塑性失稳。联立式(10)、式(12),可得管坯发生塑性失稳的临界几何条件为
 (13)
(13)
由于缩径区的初始失稳位置C(见图1)的受力状态为环向σθ≤0,轴向σz≥0,如图4所示。因此,在缩径工况下,屈服时刻的应力比ks的取值区间应为 ks≤0。由式(12)可知,在此取值区间内,当ks=0时,qs取得极大值,此时管坯缩径几何条件若满足式(13),则管坯一定发生塑性失稳。即
 (14)
(14)
根据式(10)和式(13)绘制管坯高径比L/R由1至100,厚径比δ/R分别为1/25、1/50、1/100条件下的弹性临界失稳外载曲线,并标注出L/R及δ/R值域范围内材料屈服应力σs分别为120、260、400 MPa的弹性失稳区域和塑性失稳区域如图5所示。为了体现不同弹性模量管材的共同失稳规律,图5中纵轴利用qcr/E进行了无量纲化。
如图5所示,在相同成形几何条件值域范围内,屈服应力120 MPa时管坯发生塑性失稳的尺寸范围最宽泛。这说明屈服强度越低的板材由于成形过程中越易产生塑性变形,使板材在同样的条件下塑性变形趋势比压缩失稳的趋势更强而更不易起皱。但由于材料的其他性能参数如弹性模量、屈服强度、塑性切线模量、厚向异性系数等均会对材料的抗皱性造成不同趋势的影响,每个参数的敏感性程度也不同,因此,板料最终的起皱程度是这些参数综合作用的结果。
成形几何条件对起皱程度的影响由图5可知:在特定的管坯材料工况下,若成形区高径比L/R保持恒定,则厚径比δ/R越大,失稳外载就会越远离弹性失稳区域,管坯越不易失稳;同理,若厚径比δ/R保持恒定,高径比L/R越小,失稳外载就会越远离弹性失稳区域,管坯越不易失稳。针对具体的缩径产品,管坯直径往往是固定的,因此,适度增加管坯厚度,或缩小缩径高度L,都有利于失稳程度的减弱。

图5 管材弹性临界失稳外载曲线
Fig. 5 Curves of elastic critical wrinkling load

图6 临界失稳波数n计算结果
Fig. 6 Results of critical buckling wave number n
图6所示为利用式(11)绘制的失稳波数n随管坯几何尺寸的变化规律。由式(11)可知,失稳波数主要与成形几何条件相关,材料方面仅受泊松比影响,说明不同材质相同成形几何条件的管坯起皱失稳波数差异不大。由图6可知,当缩径高径比L/R小于0.3或大于10时,不同几何条件的管坯起皱失稳波数基本相同,只有高径比L/R数值在0.3~10之间时,不同几何条件下的管坯起皱失稳波数才会有较大差异。
当缩径高度L趋近与0或无穷大时,波数趋向无穷多或无穷少,这两种趋势在管材变形的几何形态上均趋近于圆形。但显然波数越多皱纹越小,起皱程度越轻。因此,缩径高度越小,缩径成形起皱缺陷的程度也越低,这与图5从临界起皱载荷角度分析起皱趋势所得到的结论相同。
当管坯在弹性阶段未失稳,将或面临塑性失稳问题。与弹性失稳载荷的求解原理类似,塑性失稳载荷求解需在屈服外载表达式(12)的基础上累加管坯在塑性切线模量Et作用下的的临界失稳载荷计算式(10),即
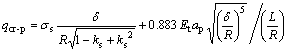 (15)
(15)
式中:Et为材料金属塑性阶段的切线模量(MPa),若材料本构关系符合幂指函数模型,即
 (16)
(16)
式中:K为强化系数(MPa);n应变硬化指数。则有
 (17)
(17)
由式(15)可知,在成形几何条件不变的情况下,通过分析单参数Et的变化,便能够体现出材料塑性阶段的强化系数K和硬化指数n对材料抗皱性的综合影响结果。即在其他成形条件相同时,切线模量Et越大的材料,材料的临界起皱应力也越大,即材料抗皱性能越强。
2 管材外压缩径工艺试验分析
2.1 管坯制备
为了验证理论方法中有关于成形几何参数及材料性能对起皱失稳程度的影响规律,选用T4态AA7075铝合金管件进行缩径成形研究。
本实验中采用国内某公司生产的厚度δ0=1.5 mm,直径D0=100 mm的T5态AA7075挤压管材,为了验证不同强度参数对起皱失稳状态的影响,对原始材料进行特定条件下的固溶处理,以获取不同屈服强度和抗拉强度的管坯进行缩径试验。
将AA7075管材用线切割机沿管材轴向切取拉伸试样。对经过固溶处理的拉伸试样和原材拉伸试样本别进行拉伸试验。图7所示为按国际标准尺寸从成形管材上切取下来的试样,采用自制的夹持端为弧形的夹具夹持零件,其弧形拉伸试样弧形一致,避免拉伸时夹持部分给实验结果带来影响。拉伸力学性能测试在Inspekt-Table100型电子万能实验机上完成,应变速率设定为1×10-3 s-1。

图7 轴向试件制备
Fig. 7 Axial specimen preparation (Unit: mm)
拉伸试验测定得到的试件真实应力-应变曲线见图8。材料在两种不同热处理条件及上述拉伸条件下的本构关系按幂指函数模型式(15)拟合后的本构方程参数K、n以及拟合精度均方差 见表1。
见表1。
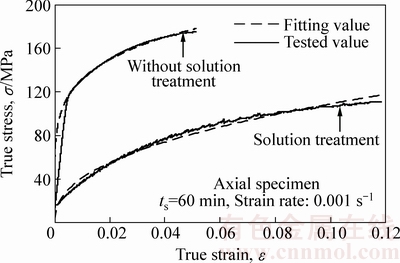
图8 AA7075管材真实应力-应变曲线
Fig. 8 Axial true stress-strain curves of AA7075 tube
表1 不同热处理条件下T5态AA7075管坯拉伸试验的本构方程参数
Table 1 Constitutive equation parameters of AA7075 tube under different solution treatment conditions

比较两种条件下的材料性能曲线,固溶处理后的坯料屈服应力下降,但塑性提高。由式(16)绘制上述两种条件下真实应变公共区间内的材料剪切模量曲线进行比较,结果如图9所示。从图9可以看出,原材的切线模量总体上大于固溶处理管材的切线模量,按照理论分析的结论,在其他影响因素相同的情况下,原材在塑性阶段的抗皱性能应优于固溶处理后的管材,但由于屈服应力参数单独对管材抗皱性能的影响趋势恰好与塑性切线模量对管材抗皱性能的影响趋势相反,若要探究具体哪个参数的影响结果在综合结果中的比重大,则需进行成形工艺试验进行探究。

图9 两种条件下材料真实应变公共区间内的塑性切线模量曲线
Fig. 9 Plastic tangent modulus curve of two materials in their common true strain region
2.2 工艺介绍
为了便捷地开展缩径试验研究,特选用固体颗粒介质成形工艺方法进行缩径试验,固体颗粒介质成形(SGMF)工艺是采用颗粒介质代替现有软模成形工艺中液体、气体或黏性介质的作用,并利用颗粒介质填充性好、易于密封、压力建立简便等特性,可在通用压力设备上实现金属管材零件内高压成形[16]。本课题组在SGMF工艺方面开展了大量的研究工作,成功试制了多种材质管、板材软模成形零件[17-18]。
固体颗粒介质缩径成形工艺原理示意图及模具照片如图10所示,通过变换缩径区高度及管坯材料进行成形试验,来探讨成形几何条件和材料性能对缩径起皱失稳的影响。
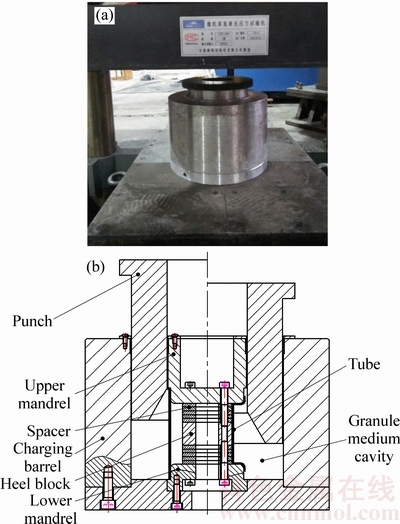
图10 模具照片及缩径工艺原理示意图
Fig. 10 Die photo (a) and schematic diagram of principle of SGMF tube outer pressure compression forming (b)
2.3 试验结果
工艺试验得到的成形零件照片如图11所示,图中L为缩径区高度,N为皱纹波数。试验管坯选用长为90 mm的AA7075管段,对母材和固溶处理后的管件分别进行不同高度的缩径成形试验。
对比同种管坯、不同缩径高度下的成形零件可知:随着缩径高度的下降,两种管坯的起皱程度均趋于减弱。试验失稳波数与理论预测失稳波数基本吻合。
对比相同缩径高度下7075原材和固溶处理后管坯的成形零件发现:在同等成形几何条件下,7075原材管坯比固溶软化后的管坯的抗皱性能强。这说明综合了材料强化系数和硬化指数影响的塑性切线模量对材料抗皱性的影响比重大于屈服应力对材料抗皱性的影响比重,对材料最终的起皱程度起主导作用。

图11 不同条件下的成形零件
Fig. 11 Different parts obtained in test under different conditions
3 结论
1) 材料在弹性变形阶段的起皱趋势受弹性模量和成形几何条件的影响;塑性阶段的起皱趋势受塑性切线模量、屈服应力及成形几何条件的影响。
2) 管坯几何条件对管材起皱的影响趋势:高径比L/R小于0.3或大于10时,不同几何条件的管坯起皱失稳波数基本相同,只有高径比L/R数值在0.3~10之间时,不同几何条件下的管坯起皱失稳波数才会有较大差异。当缩径高度L趋近与0或无穷大时,波数趋向无穷多或无穷少,这两种趋势在管材变形的几何形态上均趋近于圆形。但显然波数越多皱纹越小,起皱程度越轻。因此,缩径高度越小,缩径成形起皱缺陷的程度也越低。
3) 屈服应力以及塑性切线模量对管材塑性屈曲具有重要影响。屈服强度越低的板材在成形过程中易产生塑性变形,使板材在同样的条件下塑性变形趋势比压缩失稳的趋势更强而更不易起皱。塑性切线模量越大,材料本构关系曲线上升趋势更明显,材料刚度也更大,导致材料起皱的能力也会有所提高,即切线模量高的板材其在发生起皱后抵抗起皱高度发展的能力就越高。
由于屈服应力参数对管材抗皱性能的影响趋势恰好与塑性切线模量对管材抗皱性能的影响趋势相反,因此,影响比重大的性能参数决定管坯的实际抗皱性能。
4) 管材固体颗粒介质缩径工艺试验验证了成形几何条件对管材起皱程度的影响规律。同时也验证了塑性切线模量对材料最终的起皱程度起主导作用,塑性切线模量越大的材料,其抗皱性越强。
REFERENCES
[1] WANG You-gen, HUANG Guang-sheng, LIU Ding-kai, CHEN Lin, HAN Ting-zhuang, PENG Jian, PAN Fu-sheng. Influence of blank holder type on drawability of 5182-O aluminum sheet at room temperature[J]. Transactions of Nonferrous Metals Society of China, 2016, 26(5): 1251-1258.
[2] ABBAS H, MOHAMMAD H, GOLLO, SEYEDKASHI S M H. Process window diagram of conical cups in hydrodynamic deep drawing assisted by radial[J]. Transactions of Nonferrous Metals Society of China, 2015, 25(9): 3064-3071.
[3] JU G T, KYRIAKIDES S. Bifurcation and localization instabilities in cylindrical shells under bending—II. Predictions[J]. International Journal of Solids and Structures, 1992, 29(9): 1143-1171.
[4] HILL R. A general theory of uniqueness and stability inelastic-plastic solids[J]. Journal of the Mechanics and Physics of Solids, 1958, 6(3): 236-249.
[5] ZHOU Jing, WANG Bao-yu, LIN Jian-guo, FU Le, MA Wen-yu. Forming defects in aluminum alloy hot stamping of side-door impact beam[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(11): 3611-3620.
[6] 汤泽军, 何祝斌, 苑世剑. 内高压成形过程塑性失稳起分析[J]. 机械工程学报, 2008, 44(5): 34-38.
TANG Ze-jun, HE Zhu-bin, YUAN Shi-jian. Analysis of plastic wrinkling behavior in tube hydroforming process[J]. Chinese Journal of Mechanical Engineering, 2008, 44(5): 34-38.
[7] SUN Yong-na, WAN Min, WU Xiang-dong. Wrinkling prediction in rubber forming of Ti-15-3 alloy[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(10): 3002-3010.
[8] 梁炳文. 弹塑性稳定理论[M]. 北京: 国防工业出版社, 1983.
LIANG Bing-wen. Theory of elastoplastic stability[M]. Beijing: National Defence Industry Press, 1983: 312.
[9] KARMAN T, TSIEN H S. The buckling of thin cylindrical shells under axial compression[J]. Journal of Spacecraft and Rockets, 2003, 40(6): 898-907.
[10] TSIEN H S. A theory for the buckling of thin shells[J]. Journal of the Aeronautical Sciences (Institute of the Aeronautical Sciences), 2012, 9(10): 373-384.
[11]  Z P, CEDOLIN L. Stability of structures: Elastic, inelastic, fracture and damage theories[J]. Journal of Structural Engineering, 2010: 466-474.
Z P, CEDOLIN L. Stability of structures: Elastic, inelastic, fracture and damage theories[J]. Journal of Structural Engineering, 2010: 466-474.
[12] XUE J, FATT H. Buckling of a non-uniform, long cylindrical shell subjected to external hydrostatic pressure[J]. Engineering Structures, 2002, 24(8): 1027-1034.
[13] AGHAJARI S, ABEDI K, SHOWKATI H. Buckling and post-buckling behavior of thin-walled cylindrical steel shells with varying thickness subjected to uniform external pressure[J]. Thin-Walled Structures, 2006, 44(8): 904-909.
[14] WINTERSTETTER T A, SCHMIDT H. Stability of circular cylindrical steel shells under combined loading[J]. Thin-Walled Structures, 2002, 40(10): 893-910.
[15] BRUSH D O, ALMROTH B O. Buckling of bars, plates, and shells[M]. New York: McGraw-Hill, 1975: 463-519.
[16] DU Bing, ZHAO Chang-cai, DONG Guo-jiang, YA Yuan-yuan. Study on thin-walled tube forming by solid granule medium forming[J]. Icic Express Letters, 2014, 8: 2649-2654.
[17] DONG Guo-jiang, ZHAO Chang-cai, CAO Miao-yan. Flexible-die forming process with solid granule medium on sheet metal[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(9): 2666-2677.
[18] CAO Miao-yan, ZHAO Chang-cai, WU Li-jun, DONG Guo-jiang. Lubricant research on SGMF of magnesium alloy sheet[J]. Advanced Materials Research, 2013, 675: 311-316.
Theory and experimental research on outer pressure compression forming of thin metal tube part
DU Bing, XIE Jun, GUAN Feng-long, ZHANG Xin, ZHAO Chang-cai
(Key Laboratory of Advanced Forging & Stamping Technology and Science, Ministry of Education, Yanshan University, Qinhuangdao 066004, China)
Abstract: The main factor restricting the production and application of diameter-reduced tube parts is the wrinkling instability problem. Therefore, the wrinkling instability laws in the process of tube outer pressure compression forming were researched, and the technology methods for winkle prediction and forming quality improvement were ascertained. Based on the theory of L. H. Donnell linear buckling, the circumferential elastic and plastic wrinkling critical load expression was deduced, the influences of the forming conditions on the wrinkled morphology and the shaping property were also discussed. The AA7075 diameter-reduced tube parts by using the blank under different heat treatment conditions were produced by solid granule medium forming (SGMF) technology, and the process tests proved the conclusions of theoretical analysis.
Key words: AA7075 aluminum tube part; tube outer pressure compression forming; wrinkling instability; solid granule medium forming
Foundation item: Project(51605420) supported by the National Natural Science Foundation; Project(B935) supported by the Research Fund for the Doctoral Program of Yanshan University, China
Received date: 2017-05-11; Accepted date: 2017-09-20
Corresponding author: ZHAO Chang-cai; Tel: +86-13633333873; E-mail: zhao1964@ysu.edu.cn
(编辑 龙怀中)
基金项目:国家自然科学基金资助项目(51605420);燕山大学博士基金资助项目(B935)
收稿日期:2017-05-11;修订日期:2017-09-20
通信作者:赵长财,教授,博士;电话:13633333873;E-mail:zhao1964@ysu.edu.cn