J. Cent. South Univ. Technol. (2010) 17: 888-894
DOI: 10.1007/s11771-010-0572-7
First-principle investigation on electronic structures and elastic properties of Al-doped MoSi2
LIU Xiao-liang(刘小良)1, 2, REN Yi(任意)2, XU Hui(徐慧)2, ZHAO Zhong-wei(赵中伟)1
1. School of Metallurgical Science and Engineering, Central South University, Changsha 410083, China;
2. School of Physical Science and Technology, Central South University, Changsha 410083, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2010
Abstract: The electronic structures and elastic properties of Al-doped MoSi2 were calculated using the plane wave pseudo-potential method based on the density functional theory, in which the generalized-gradient approximation (GGA) was used to describe the exchange-correlation potential. Starting from the elastic constants, bulk modulus, shear modulus, elastic modulus and Poisson ratio of Al-doped MoSi2 were obtained by using the Hill method. The results indicate that conductivity of Al-doped MoSi2 is improved to some extent in comparison with that of pure MoSi2 due to the orbit hybridization of Mo 4d, Al 3p and Si 3p electrons. In addition, calculations show that the elastic modulus and the brittleness of Al-doped MoSi2 are smaller than those of pure MoSi2, which implies that it is feasible to toughen MoSi2 by doping Al. The agreement of the conclusion with experiment shows that the present theory is reasonable.
Key words: MoSi2; Al-doping; electronic structures; elastic properties; first-principle
1 Introduction
MoSi2 has many excellent properties of both metals and ceramics, such as high melting point, high temperature oxidation resistance, good thermal and electrical conductivity and low linear expansion coefficient. It is believed that MoSi2-based high temperature structural materials are highly competitive materials after Ni-Mo superalloys and structural ceramics [1-4]. Since the emergence of MoSi2 heating elements that can work at temperatures above 1 773 K in air environment, MoSi2 heating elements have become the mainstream of high-temperature heating elements [5-6]. Industrial applications mainly include furnace elements and components, power generation components, and high temperature heat exchangers. Aerospace applications mainly include hot spot components of turbine aircraft engine such as combustors, vanes, and seals. But some properties of MoSi2, such as room temperature brittleness, poor low-temperature oxidizability and low high-temperature strength, considerably limit its further application.
However, the inherent limitations of MoSi2 may be improved to some extent by alloying [7-9]. Among all studies on doping modification of MoSi2 alloys, Al-doped MoSi2 alloy has been widely studied in experiments at present. These researches suggest that the proportion of metallic bonding is increased and the symmetry of crystal structure is improved when Al atoms substitute Si atoms in unit cell of MoSi2 in the alloying process. Theoretically, with the development of first- principle method [10-13], some properties of MoSi2 were numerically studied, but there were few first- principle researches on the electronic structures and elastic properties of Al-doped MoSi2. Thus, in this work the electronic structures and elastic properties of Al-doped MoSi2 were systematically studied by using the Cambridge Serial Total Energy Package (CASTEP) module [14] of Material Studio (MS) that is based on density function theory (DFT) and pseudo-potential.
2 Model and method
MoSi2 has the C11b-type crystal structure [15] with space group and the experimental lattice parameters are a=b=0.320 2 nm, c=0.784 3 nm [16]. In its crystal structure, Mo—Mo bonds are metal bonds and Si—Si bonds are covalent bonds, while Mo—Si bonds are metallic-covalent mixed bonds.
and the experimental lattice parameters are a=b=0.320 2 nm, c=0.784 3 nm [16]. In its crystal structure, Mo—Mo bonds are metal bonds and Si—Si bonds are covalent bonds, while Mo—Si bonds are metallic-covalent mixed bonds.
Based on C11b-type MoSi2, 2×2×1 MoSi2 super cell with 24 atoms is built, and some of Si atoms are replaced by Al atoms. Al-doped MoSi2 can be represented by Mo(Si1-xAlx)2, in which x is the molar ratio of Al to Si of the compound. Experimental results proved that the crystal structure of Mo(Si1-xAlx)2 should change from C11b to C40, and even further to orthorhombic C54 with the increase of Al doping concentration x [9, 17]. In this work, the value of x changes in the range from 0 to 0.25 so that Mo(Si1-xAlx)2 can maintain its body-centered cubic C11b-type structure.
A super cell of Mo(Si1-xAlx)2 with C11b-type crystal structure was focused on, and its electronic structures and elastic properties were numerically calculated by using plane wave pseudo-potential (PWP) method [18-19]. The super cell was firstly optimized by Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm, which provided a fast way of finding the lowest energy structure in CASTEP code. The optimization was performed if the forces on the atoms are not more than 4.8×10-11 N (0.3 eV/nm) and all the stress components are less than 0.05 GPa. The tolerance in the self- consistent field calculation is 1×10-6 eV/atom. Ultrasoft pseudopotentials were expanded in a plane wave basis set with a 420 eV cutoff energy in the process of calculation. Electron exchange and correlation effect are shown in the scheme of PW91 in GGA. The sampling k-points are 8×8×11 according to Monkhorst-Pack grid.
3 Electronic structure and population analysis
3.1 Lattice parameters
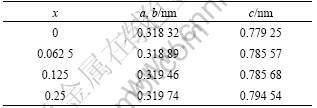
Firstly, Mo(Si1-xAlx)2 crystals with different x values were optimized. The lattice parameters of optimized structure, a(b) and c, are listed in Table 1. It is clear that the lattice parameters of Al-doped MoSi2 slightly increase with the increase of x, because the atomic radius of Al atom is greater than that of Si atom.
Table 1 Lattice variation of Mo(Si1-xAlx)2 due to substitution of Al to Si
3.2 Energy band and electronic density of states
Fig.1 shows the energy band and electronic density of states (DOS) of Mo(Si1-xAlx)2 with x equal to 0.062 5, 0.125 and 0.25, while Fig.2 shows the corresponding properties of pure MoSi2 for comparison. The dashed line maps the location of Fermi surface, which corresponds to the energy of zero.
From Figs.1 and 2, it is found that Mo(Si1-xAlx)2 and MoSi2 share some common features in their energy band structures and electronic DOS. There are two peaks of DOS in the region of high-energy anti-bonding states and low-energy bonding states near the Fermi surface, respectively. While there is a low valley of electronic DOS that distinguishes high-energy anti-bonding states and low-energy bonding states. But the DOS at the valley bottom is not equal to zero (about 0.32 eV-1), which suggests that valence band and conduction band overlap each other partially. Hence, both Mo(Si1-xAlx)2 and pure MoSi2 crystal exhibit the properties of semimetal, and their conductivities lie between those of semiconductors and metals [20].
In addition, the effect of substitution of Al for Si on the electronic structure of MoSi2 can be found from Figs.1 and 2. In order to highlight the electronic structure properties of Mo(Si1-xAlx)2 near the Fermi surface, Fig.3 shows the total electronic DOS and partial DOS (PDOS) near the Fermi surface. The total DOS and PDOS of pure MoSi2 are shown in Fig.4.
Comparing Fig.3 with Fig.4, it is found that the DOS spectra change with the variation of x and the valley in the vicinity of Fermi surface has a tendency of blue-shift, which leads to a successive increase of DOS on the Fermi surface from 0.32 eV-1 (x=0) to 0.87 eV-1 (x=0.062 5), 1.26 eV-1 (x=0.125), 1.96 eV-1 (x=0.25). Given that electrons close to Fermi surface play a decisive role in electrical properties of materials, it can be concluded that the conductive performance of MoSi2 is improved after the incorporation of Al.
The PDOS in Fig.3 indicates that the contribution of d electrons to the total DOS near Fermi surface is relatively great, while that of s electrons is very small. Moreover, comparatively speaking, the DOS of 4d electrons of Mo atoms is higher than that of 3p electrons of Al atoms and Si atoms in the region close to Fermi surface. Therefore, the conductive properties of Mo(Si1-xAlx)2 are mainly determined by d electrons.
In order to provide further support to the conclusions above, the electronic DOSs of Al, Si and Mo in Mo(Si1-xAlx)2 with x=0.25 were calculated. As shown in Fig.5, DOSs of Al and Si are very small in the vicinity of Fermi surface and the total DOS mainly comes from Mo atom. More precisely, it can be concluded that the conductive properties of Mo(Si1-xAlx)2 mainly come from 4p electrons of Mo atom. Although Al atom has little direct contribution to the total DOS of Mo(Si1-xAlx)2 near the Fermi surface, the hybridization of Al 3p electrons, Mo 4d electrons and Si 3p electrons improves conductive properties of MoSi2. The hybridization can be illustrated by using population analysis in Ref.[21].
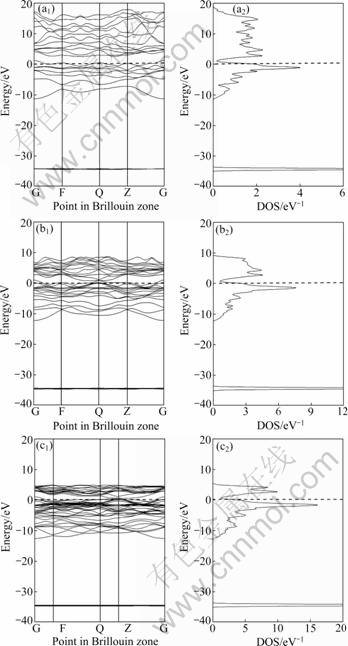
Fig.1 Energy bands and electronic DOS of Mo(Si1-xAlx)2 with different x values: (a1) x=0.062 5, energy band; (a2) x=0.062 5, electronic DOS; (b1) x=0.125, energy band; (b2) x=0.125, electronic DOS; (c1) x=0.25, energy band; (c2) x=0.25, electronic DOS
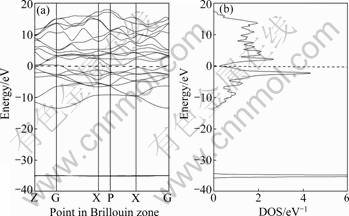
Fig.2 Energy band (a) and electronic DOS (b) of pure MoSi2
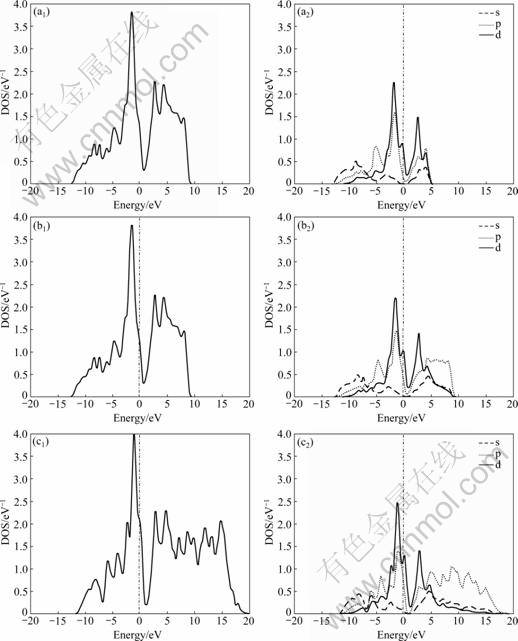
Fig.3 Total DOS and PDOS of Mo(Si1-xAlx)2 with different x values: (a1) x=0.062 5, total DOS; (a2) x=0.062 5, PDOS; (b1) x=0.125, total DOS; (b2) x=0.125, PDOS; (c1) x=0.25, total DOS; (c2) x=0.25, PDOS
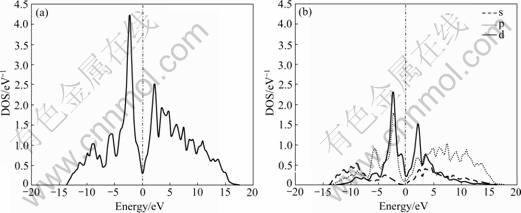
Fig.4 Total DOS (a) and PDOS (b) of pure MoSi2
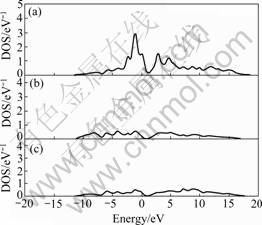
Fig.5 DOSs of Mo (a), Si (b) and Al (c) in Mo(Si1-xAlx)2 with x=0.25
3.3 Population analysis
Charge populations of Mo(Si1-xAlx)2 with x=0.25 were calculated by means of Milliken analysis. The results are listed in Table 2. Given the outer-shell electron configurations 3s23p1, 3s23p2, 4s24p64d55s1 of atoms Al, Si and Mo respectively, it can be found that s electrons significantly reduce for all atoms while electrons occupying p orbit (Al and Si) and d orbit (Mo) increase in the compound, and the Milliken charges are determined to be +0.38e for Al atom, +0.15 e for Si atom and -0.53 e for Mo atom. According to empirical electron theory of solids and molecules [22-24], it is believed that some of s electrons transit into p and d orbits to participate in the p-d hybridization in bonding process. Hence, the total DOS close to Fermi surface mainly comes from orbit hybridization of Mo 4d electrons, Al 3p electrons and Si 3p electrons.
4 Elastic properties
In this section, the elastic constants (Cij) of Mo(Si1-xAlx)2 were computed with the same parameter settings mentioned above. To confirm the reliability of this calculation, the elastic constants of pure MoSi2 were calculated. The results are listed in Table 3. The elastic constants obtained by experiment are also listed for comparison. It is clear that the calculated results basically agree with experimental data. Then, the elastic constants of Mo(Si1-xAlx)2 with x=0.125 and x=0.25 were calculated. Some elastic constants and their corresponding compliances (Sij) are listed in Table 4.
Now, the obtained elastic constants were used to estimate the elastic properties of Mo(Si1-xAlx)2 crystal. Within the Reuss approximation, bulk modulus (BR) and shear modulus (GR) are given by:
 (1)
(1)
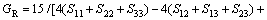
 (2)
(2)
While in the Voigt approximation, bulk modulus (BV) and shear modulus (GV) are given by:
 (3)
(3)
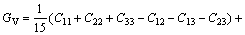
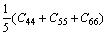 (4)
(4)
In Hill model [26], bulk modulus (BH), shear modulus (GH), elastic modulus (E) and Poisson ratio (ν) are defined as
 (5)
(5)
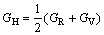 (6)
(6)
 (7)
(7)
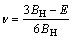 (8)
(8)
Substituting the results of Table 4 into Eqs.(1)-(8), bulk modulus, shear modulus, elastic modulus and Poisson ratio of Mo(Si1-xAlx)2 can be obtained. The results are listed in Table 5.
It is clear that the obtained bulk modulus (BR, BV and BH) and shear modulus (GR, GV and GH) of Mo(Si1-xAlx)2 decrease with the increase of x. However, so far there are no experimental data available to verify these calculated results.
According to the empirical criterion proposed by PUGH [27], the ratio of bulk modulus to shear modulus presents a measurement for machinable behavior. A high B/G value is associated with ductility but a low value indicates brittleness. The critical value that separates ductile and brittle behaviors is around 1.75. As shown in Table 5, the calculated BH/GH values are 1.17, 1.40, 1.52,
Table 2 Atomic charge populations of Mo(Si1-xAlx)2 with x=0.25

Table 3 Elastic constants (in GPa) of MoSi2 crystal

Table 4 Elastic constants (in GPa) and their corresponding compliances (in 10-3 GPa-1) of Mo(Si1-xAlx)2 crystal with x=0.125 and 0.25

Table 5 Bulk modulus, shear modulus, elastic modulus and Poisson ratio of Mo(Si1-xAlx)2 crystal with x=0, 0.125 and 0.25

for MoSi2, Mo(Si0.875Al0.125)2 and Mo(Si0.75Al0.25)2, respectively. Those ratios indicate the brittleness of Mo(Si1-xAlx)2 is reduced compared with MoSi2. In addition, Poisson ratio can also be used to measure the brittleness and ductility of metallic and intermetallic compounds. Generally speaking, Poisson ratio for ductile materials is about 0.33, while less than 0.33 for brittle materials. Poisson ratios listed in Table 5 suggest that the ductility of Al-doped MoSi2 is improved. Experimental results reported in Refs.[20, 28] proved that the addition of Al has toughening efficiency to MoSi2, and the toughening efficiency depends on the concentration of Al. Calculated results in this work agree with the experimental results qualitatively and prove that it is feasible to toughen MoSi2 by doping Al.
5 Conclusions
(1) The electronic structures and elastic properties of Al-doped MoSi2 crystals Mo(Si1-xAlx)2 are computed by using the plane wave pseudo-potential method based on the density functional theory.
(2) The substitution of Al for Si increases the electric conductivity of MoSi2, and 4d electrons of Mo atom play a major role in conductive properties. Though the DOS of Al is very small in the vicinity of Fermi surface, the hybridization of Al 3p electrons, Mo 4d electrons and Si 3p electrons improves conductive property of MoSi2.
(3) The elastic constants of Mo(Si1-xAlx)2 crystals are calculated and their elastic modulus, shear modulus, bulk modulus and Poisson ratio are estimated using Hill model. The results show that the bulk modulus of Al- doped MoSi2 is smaller than that of MoSi2 and the brittleness of Al-doped MoSi2 is reduced, which implies that it is feasible to toughen MoSi2 by doping Al.
References
[1] WANG De-zhi. The study on synthesis, microstructure and properties of MoSi2 and MoSi2-based composites [D]. Changsha: Central South University, 1998: 1-98. (in Chinese)
[2] PETROVIC J J, VASUDEVAN A K. Key developments in high temperature structural silicides [J]. Materials Science and Engineering A, 1999, 261(1/2): 1-5.
[3] VASUDEVAN A K, PETROVIC J J. A comparative overview of molybdenum disilicide composites [J]. Materials Science and Engineering A, 1992, 155(1/2): 1-17.
[4] JIANG Wan, ZHAO Shi-ke, WANG Gang. Progress in the research of molybdenum disilicide and its applications [J]. Journal of Inorganic Materials, 2001, 16(4): 577-585. (in Chinese)
[5] LIU Fang, FAN Wen-jie, CHEN Yu-chao. The preparation of high quality Si-Mo element in electro-heating [J]. Refractories, 2003, 5(3): 304-305. (in Chinese)
[6] GAO Jian-ying, JIANG Wan, LI Jian-lin, WU Li-bin. Progress in alloying and doping of MoSi2 [J]. China Molybdenum Industry, 2003, 27(4): 23-27. (in Chinese)
[7] HARADA Y, MURATA Y, MORINAGA M. Solid solution softening and hardening in alloyed MoSi2 [J]. Intermetallics, 1998, 6(6): 529-535.
[8] PETROVIC J J. Toughening strategies for MoSi2-based high temperature structural silicides [J]. Intermetallics, 2000, 8(9/10/11): 1175-1182.
[9] SHARIF A A, MISRA A, PETROVIC J J, MITCHELL T E. Alloying of MoSi2 for improved mechanical properties [J]. Intermetallics, 2001, 9(10/11): 869-873.
[10] HUANG Ke-long, CHEN CHUN-an, LIU Su-qin, LUO Qiong. First-principle investigation on stability of Co-doped spinel λ-Mn4-xCoxO8 [J]. Journal of Central South University of Technology, 2007, 14(2): 186-190.
[11] ZHOU S H, WANG Y, JIANG C, ZHU J Z, CHEN L Q, LIU Z K. First-principles calculations and thermodynamic modeling of the Ni-Mo system [J]. Materials Science and Engineering A, 2005, 397(1/2): 288-296.
[12] LIU Xiao-liang, ZHAO Zhong-wei, XU Hui, LI Yang-feng. First-principle study on the electronic structures and optical properties of MoSi2 and WSi2 single crystals with the C11b structure [J]. Journal of Central South University of Technology, 2009, 40(3): 568-574. (in Chinese)
[13] DUMAN S, BA?CI S, T?T?NC? H M, SRIVASTAVA G P. First-principles studies of ground-state and dynamics of MgS, MgSe and MgTe in the rocksalt, zinc blende, wurtzite, and nickel arsenide phase [J]. Physical Review B, 2006, 73: 205201.
[14] SEGALL M D, LINDAN P J D, PROBERT M J. First-principles simulation: Ideas, illustrations and the CASTEP code [J]. J Phys: Cond Matt, 2002, 14(11): 2717-2743.
[15] UMAKOSHI Y, SAKAGAMI T, HIRANO T. High temperature deformation of MoSi2 single crystals with the C11b structure [J]. Acta Metall Mater, 1990, 38(6): 909-915.
[16] NIE Yao-zhuang, XIE You-qing, PENG Hong-jian, LI Xiao-bo. Elastic and thermal properties of Zr5Si3 and Zr3Ti2Si3 [J]. The Chinese Journal of Nonferrous Metals, 2007, 17(9): 1495-1500. (in Chinese)
[17] LIU Y, SHAO G, TSAKIROPOULOS P. Thermodynamic reassessment of the Mo-Si and Al-Mo-Si systems [J]. Intermetallics, 2000, 8(8): 953-962.
[18] TROULLIER N, MARTINSJ L. Efficient pseudopotentials for plane-wave calculations [J]. Physical Review B, 1991, 43(15): 1993- 2006.
[19] KRESSE G, FURTHMULLER J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set [J]. Physical Review B, 1996, 54(16): 11169-11186.
[20] ZHANG Hou-an, XU Jian-guang, YAN Jian-hui. Preparation and properties of MoSi2 and MoSi2-based composites [M]. Beijing: Defense Industry Press, 2007: 18-62. (in Chinese)
[21] ZHANG Yue, GU Jing-hua, SHANG Jia-Xian. Foundation of computational materials science [M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2007: 37-91. (in Chinese)
[22] ZHOU Fei. Study on the structure and properties for MoSi2 and WSi2 phases by electron theory [J]. Journal of the Chinese Ceramic Society, 2000, 28(5): 462-464. (in Chinese)
[23] ZHANG Rui-lin. Empirical electron theory of solids and molecules [M]. Changchun: Jilin Science Press, 1993: 45-132. (in Chinese)
[24] PERDEW J P, WANG Y. Accurate and simple analytic representation of the electron-gas correlation energy [J]. Physical Review B, 1992, 45(15): 13244-13249.
[25] NAKAMURA M, MATSUMOTO S, HIRANO T. Elastic constants of MoSi2 and WSi2 single crystals [J]. Journal of Materials Science, 1990, 25(7): 3309-3313.
[26] ANDERSON O L. A simplified method for calculating the Debye temperature from elastic constants [J]. Journal of Physics and Chemistry of Solids, 1963, 24(7): 909-917.
[27] PUGH S F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals [J]. Philosophical Magazine, 1954, 45: 823-843.
[28] TABARU T, SHOBU K, SAKAMOTO M, HANADA S. Effects of substitution of Al for Si on the lattice variations and thermal expansion of Mo(Si,Al)2 [J]. Intermetallics, 2004, 12(1): 33-41.
(Edited by CHEN Wei-ping)
Foundation item: Project(20080431025) supported by Chinese Postdoctoral Science Foundation; Project(08JJ3005) supported by Hunan Provincial Natural Science Foundation of China; Project(2007) supported by Postdoctoral Science Foundation of Central South University, China
Received date: 2009-12-18; Accepted date: 2010-03-27
Corresponding author: ZHAO Zhong-wei, PhD, Professor; Tel: +86-731-88830476; E-mail: zhongweizhao@hotmail.com