J. Cent. South Univ. (2016) 23: 701-707

DOI: 10.1007/s11771-016-3115-z

Experimental study and analysis on fatigue stiffness of RC beams strengthened with CFRP and steel plate

LU Yi-yan(卢亦焱), HU Ling(胡玲), LI Shan(李杉), WANG Kang-hao(王康昊)

School of Civil Engineering, Wuhan University, Wuhan 430072, China

 Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: The objective of this work is to investigate the fatigue behavior of reinforced concrete (RC) beams strengthened with externally bonded carbon fiber reinforced polymer (CFRP) and steel plate. An experimental investigation and theoretical analysis were made on the law of deflection development and stiffness degradation, as well as the influence of fatigue load ranges. Test results indicate that the law of three-stage change under fatigue loading is followed by both midspan deflection and permanent deflection, which also have positive correlation with fatigue load amplitude. Fatigue stiffness of composite strengthened beams degrades gradually with the increasing of number of cycles. Based on the experimental results, a theoretical model by effective moment of inertia method is developed for calculating the sectional stiffness of such composite strengthened beams under fatigue loading, and the calculated results are in good agreement with the experimental results.

Key words: carbon fiber reinforced polymer; steel plate; composite strengthening technique; reinforced concrete beams; fatigue stiffness

1 Introduction

Worldwide concern about the deterioration of bridges has prompted extensive research efforts to find effective and economical rehabilitation technique. Externally bonded carbon fiber reinforced polymer (CFRP) and externally bonded steel plate are two typical ones.

Externally bonded CFRP composites, as a promising rehabilitation system to upgrade reinforced concrete (RC) beams, have been examined in the literature due to their excellent properties [1-4], such as their superior properties in the areas of resistance to heat and corrosion, high strength to weight ratio, good fatigue resistance, and their versatility of use. It is proved that CFRP strengthening system can significantly enhance the strength and stiffness, thus largely improve the load-carrying capacity of the beams, but this accompanies with some reduction of ductility [5-7]. In addition, it is not easy to anchorage CFRP material [8].

Externally bonded steel plate, as a conventional strengthening technique which has low prices and wide availability, contributes to a good ductility of a strengthened beam throughout the entire loading process [9-11]. However, the thickness and layers of strengthened steel plate are restricted so as to meet the requirements of balanced-reinforced beam, and steel plate should meet the shape of the reinforced member for steel plate is not as flexible as carbon fiber sheets.

In order to make full use of advantages of the two kinds of strengthening materials and make up for deficiencies of a single material strengthening method, the composite strengthening technique may be a good choice [12-13], which can improve the load-carrying capacity of the beam, solve the problem of anchoring CFRP, in the meanwhile, improve the ductility of the reinforced member and make the construction process more convenient.

Although extensive experimental and analytical studies had been conducted on FRP-strengthened or steel plate-strengthened RC beams, rare attempt was made to strengthen RC beams combined with CFRP sheets and steel plate. Previous work about composite strengthening mainly focused on the static behavior of RC beams strengthened by this composite technique [14-15], little is known of the fatigue performance of such composite strengthening system. Moreover, it is necessary to investigate their long-term performance considerably before this composite strengthening technique gain full acceptance.

In the present work, a study was made in the program in order to make full use of advantages of the two kinds of materials in improving fatigue performance of RC beams. The objectives of this work are: 1) to clarify the effectiveness of composite strengthening technique; 2) to study the law of deflection development under fatigue loading and the influence of fatigue load ranges on it; 3) to develop a theoretical model for the section fatigue stiffness.

2 Experimental program

2.1 Test beams details

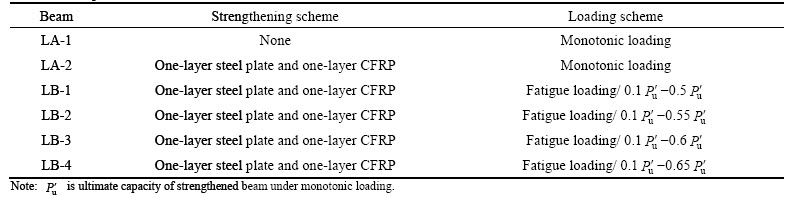
A total of six full-scale beams were tested in the study and the geometry of the original beams is shown in Fig. 1. Each beam has two tensile reinforcing bars of D16 (diameter 16 mm) and two compressive steel bars of D10 (diameter 10 mm). Shear reinforcement consisted of 8 mm-diameter round steel stirrups with a spacing of 250 mm in pure flexure sections and 100 mm in flexure-shear sections, so as to prevent shear failure of the beams during the loading process, as shown in Fig. 1. The details of the six beams tested are shown in Table 1. Among the six beams, two beams were tested under static load marked as “LA” series and four beams were tested under repetitive fatigue loads marked as “LB” series. In addition, the beam LA-1 was tested as control beam without strengthening; the other beams were strengthened with one-layer steel plate and one-layer CFRP sheet externally bonded on the tensile soffit and anchored with steel U-hoops by means of bolts (Fig. 2).

2.2 Material properties

The average 28-day concrete cube strength was 38.66 MPa, cylinder strength was 30.54 MPa, and an elastic modulus of 32.28 GPa. The measured yield strength values of the 8 mm and 10 mm round rebar and 16 mm deformed rebar were 390, 360 and 380 MPa, respectively. The steel plate used in the test was 2500 mm long by 100 mm wide by 2 mm thick, with its yield strength of 310 MPa and elongation of 23.4%. The CFRP material consisted of 2500 mm long, 150 mm wide and 0.111 mm thick carbon fiber sheet externally bonded to the tension face of the concrete beams using a two-part epoxy mixed at 3:1 ratio and cured at room temperature. Tensile strength, modulus, and elongation of the CFRP were 2800 MPa, 235 GPa, and 2.42%, respectively.

Fig. 1 Geometry and steel reinforcement of beams (Unit: mm)

Fig. 2 Strengthening method and measurement layout (Unit: mm)

Table 1 Test specimen

2.3 Measurement and test procedure

All beams were tested in four-point bending over a 2.7 m simple span. Figure 2 shows the location of measuring sensors including strain gauges and linear variable displacement transducers (LVDTs). A total of three LVDTs were used to measure midspan, and supporting points’ deflection. The strain data and deflection data were recorded automatically by a computer through a DHDAS signal system.

Static load test was conducted on a 5000-kN hydraulic actuator for specimens LA-1 and LA-2 in order to obtain the ultimate capacity of the strengthened and unstrengthened beams, which was the basis to determine the minimum and maximum fatigue loads applied. Constant amplitude fatigue test was carried out for the remaining four beams. Fatigue test setup is shown in Fig. 3. The fatigue test was conducted on a FTS multifunction servo-control system and in load control with sinusoidal applied loads being cycled at 3 Hz from a lower bound to a upper bound calculated in proportion to the static load test results, as indicated in the loading scheme section in Table 1. Since fatigue testing is a very time-consuming and expensive process, an upper limit of the number of cycles i.e. 2×10⁶ cycles, to be applied was selected. The test was terminated as and when the failure of the specimen occurred or this upper limit was reached whichever was earlier. Specimens that did not fail after 2×10⁶ cycles were monotonically loaded to failure so as to study their residual static mechanical behavior.

Fig. 3 Test setup

3 Experimental results

3.1 Failure modes

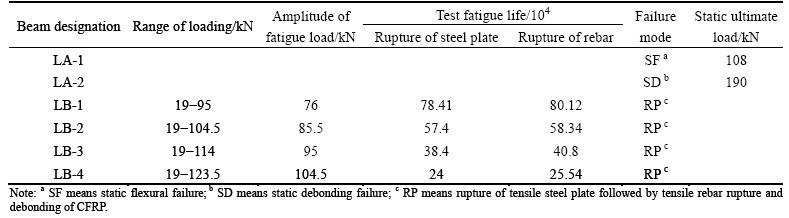
There were three failure modes observed in the test, as shown in Fig. 4. The reference beam LA-1 without strengthening subjected to static loading was identified as typical flexural failure, as shown in Fig. 4(a). The failure of strengthening beam LA-2 subjected to static loading was classified as debonding failure, as shown in Fig. 4(b). the failure initiated at the peeling of bottom CFRP in the vicinity of steel U-hoop. when the load reached 190 kN and sustained, the bottom steel plate and CFRP debonded from concrete substrate entirely at the pure flexure section, which indicated that further anchorage measures should be applied when CFRP and steel plate composite strengthening technique was used. For the composite strengthened beams subjected to fatigue loading (i.e. LB-1, LB-2, LB-3, LB-4), the tensile steel plate ruptured at somewhere located near the crack in the midspan when the fatigue load cycles to hundreds of thousands of times. At this moment, tensile rebar and CFRP continued to sustain the fatigue load and CFRP started peeling off from the concrete substrate gradually. After 10×10³ to 20×10³ cycles, CFRP delaminated from the concrete substrate in a large area, and fractured off in a certain location. Then, the beam failed at this time, as indicated in Fig. 4(c). The results for fatigue loading cycles and failure modes are listed in Table 2.

Fig. 4 Failure modes of beams:

Table 2 Test results

3.2 Load-deflection behavior

The monotonic response to failure of ‘LA’ series beams under static load is shown in Fig. 5. It is observed from Fig. 5 that composite strengthening technique raises the peak point of the load-deflection curve and increases the slope of the curve. As a result, ultimate load increases and the deflection growth rate slows down. The main reason is that strengthening material inhibits crack formation, delays crack propagation and thus enhances the strength and stiffness of the beam significantly.

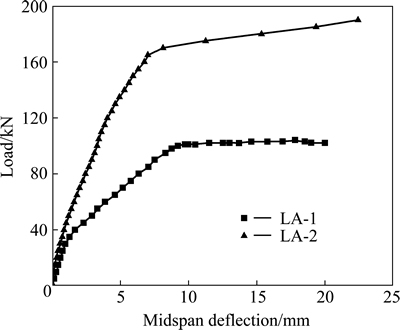
Fig. 5 Load-deflection curves for static test

The response of the fatigue-loaded specimen LB-2 at different numbers of cycles is shown in Fig. 6. It is indicated from Fig. 6 that with the increase of number of cycles, the slope of the curve reduces slightly, and when it closes to failure, the deflection grows faster. Meanwhile, it is observed from abscissa values that permanent deflection remains after unloading every cycle, and the permanent deflection of the beam increases gradually with the increase of the number of cycles, which gives an indication of damage accumulation and stiffness degradation.

The midspan deflection versus number of cycles due to fatigue for all “LB” series beams is given in Fig. 7. As shown in Fig. 7, the greater the load range is, the larger the midspan deflection is, and the development of midspan deflection is divided into three stages. At the first stage, the midspan deflection grows rapidly, and then enters into the second stage of relative stable growth, followed by an abrupt increase of midspan deflection at the third stage. In addition, the same law is also found in the permanent deflection measured in the fatigue test, which is shown in Fig. 8. Thus, it is indicated that fatigue stiffness of composite strengthened beams degrades gradually with the increasing of number of cycles.

Fig. 6 Load versus deflection response of LB-2

Fig. 7 Midspan deflection versus number of cycles

4 Theoretical model for section fatigue stiffness

In this section, the theoretical model for section fatigue stiffness of composite strengthened beam was developed by effective moment of inertia method.

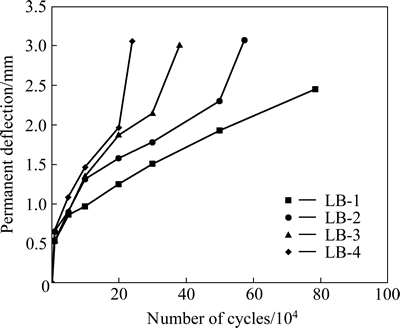
Fig. 8 Permanent deflection versus number of cycles

4.1 Basic assumption

According to the experimental results and the related theories of reinforced concrete beams [16], the basic calculating assumptions of composite strengthened beam are as follows:

1) The deformation of the cross section accords with plane section assumption.

2) Bond between CFRP and steel plate as well as that between CFRP and concrete substrate is sound until the beam fails.

3) Regardless of the concrete tensile strength in the tensile zone, tensile stresses are all shared by reinforcing bar, steel plate and CFRP sheets.

4) Concrete stress distribution in the compressive zone is triangular distribution.

4.2 Computation of section fatigue stiffness

Based on Balaguru and Shah’s model [17] reported in 1982, two major contributing factors can be summarized for the beams subjected to fatigue loading: cyclic creep of concrete, and degradation of flexural stiffness due to increase in cracking and reduction in modulus of rupture under fatigue loading. Balaguru and Shah [17] proposed an equation of the cyclic creep strain in concrete based on experimental results as follows:

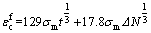                     (1)

where 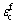 is the cyclic creep strain; Δ is the stress range expressed as a fraction of the compressive strength, s_m is the mean stress expressed as a fraction of the compressive strength, 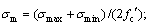s_max is the maximum applied compressive stress in concrete; s_min is the minimum applied compressive stress in concrete; N is the number of cycles; t is the time from start of loading.

Once the cyclic creep strain is known, the cycle- dependent secant modulus for concrete in compression  can be expressed as

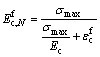                            (2)

where E_c is the initial secant modulus; 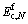 is the cyclic modulus of concrete after number of cycles N.

The depth of the neutral axis, x_cr, can be calculated using the force equilibrium equation. The contribution of steel plate and CFRP sheets are considered to be similar to the contribution of steel reinforcement. The main principle is that the steel bar and strengthening materials on the cross section can be converted into equivalent conversion section of concrete through elastic modulus ratio. The area of the steel bar, CFRP sheets and steel plate is multiplied by the modular ratios α_E, α_f, α_a respectively.

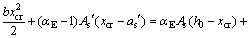
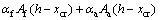               (3)

where A_s is the cross-sectional area of the reinforcing bars in tension side; A_f is the cross-sectional area of the CFRP sheets in tension face; A_a is the cross-sectional area of the steel plate in tension face; b is the width of the beam; h₀ is the depth of the reinforcing bars in the tension side; x_cr is the depth of the neutral axis; h is the thickness of the beam; α_E is the modular ratio of steel reinforcement given by equation, 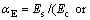  E_s is the modulus of elasticity of the reinforcing bars; α_f is the modular ratio of the CFRP sheets given by the equation:  E_f is the modulus of elasticity of the CFRP sheets; α_a is the modular ratio of the steel plate given by equation: 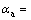  E_a is the modulus of elasticity of the steel plate.

Once the depth of the neutral axis is known, the moment of inertia of cracked section, I_cr, can be calculated as

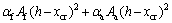              (4)

The maximum stress in concrete s_max and the minimum stress in concrete s_min can be calculated using I_cr and mechanics principle:

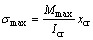                             (5)

                              (6)

where M_max is the maximum applied moment; M_min is the minimum applied moment.

Once s_max and s_min in concrete are known, the cycle-dependent modulus 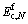 for a given number of cycles can be calculated using Eqs. (1) and (2).

In the case of static loading, the contribution of concrete in the tension zone is accounted for by using the effective moment of inertia [18], which is expressed by

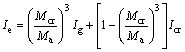               (7)

where I_e, I_cr and I_g are the effective, cracked and gross moment of inertia; M_a is the maximum value of the applied moment along the beam; M_cr is the cracking moment given by  where f_r is the modulus of rupture of concrete  given by 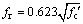 and 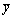 is the distance from centroidal axis of gross section, neglecting reinforcement, to tension face.

In the case of fatigue loading, the stiffness of the beam will reduce progressively with the number of cycles. This is due to the fatigue of concrete in the tension zone, which can be accounted for by means of a reduced cycle-dependent modulus of rupture [19], and can be expressed as

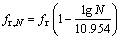                        (8)

It should be noted that the modulus of rupture f_r and the cracking moment M_cr will reduce with the increase of the number of fatigue cycles, and consequently lead to the reduction of the effective moment of inertia I_e. Thus, the cracking moment M_cr and the effective moment of inertia I_e change to 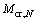 and  after N cycles, respectively, which are given by Eqs. (9) and (10):

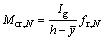                            (9)

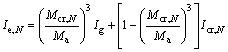        (10)

where I_cr,N is the moment of inertia after N cycles calculated using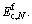

The flexural stiffness degradation is interpretated by the term M_cr,N while the effect of the concrete creep is included in the terms of 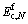 and I_cr,N.

For the fatigue loading, the deflections are calculated using the effective moment of inertia after N cycles I_e,N and the cycle modulus of concrete after N cycles 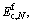 that is:

                           (11)

where d is the instantaneous deflection; f(load, span) is a function for the particular load and span arrangement; 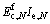 is the reduced stiffness of the beam after N number of cycles.

4.3 Comparison of analytical and experimental results

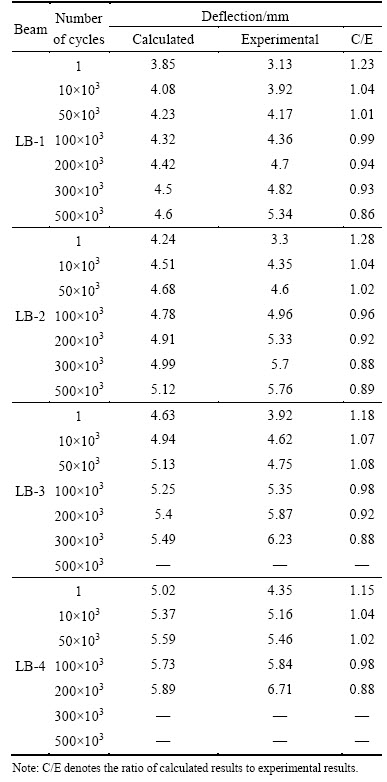
Comparison of experimental and calculated deflection values at different number of cycles for each composite strengthened beam subjected to fatigue loading are presented in Table 3. The mean value of the ratio of calculated results to experimental results is 1.0075, the standard deviation is 0.11246, and the variable coefficient is 0.11162. It is evident that there is a good consistency between the analytical and experimental value. Thus, it is indicated that the analytical model does predict the reduction of the section fatigue stiffness of composite strengthened beams.

Table 3 Comparison of calculated results and experimental results

5 Conclusions

1) Composite strengthening technique can not only improve the ultimate load-carrying capacity largely but also enhance the flexural stiffness of the RC beams effectively, which contributes to retarding the deflection development of strengthened beams.

2) Permanent deflection is generated from composite strengthened beams subjected to fatigue loading. The law of three-stage change under fatigue loading is followed by both midspan deflection and permanent deflection, which also have positive correlation with fatigue load amplitude. Fatigue stiffness of composite strengthened beams degrades gradually with the increasing of number of cycles.

3) Effective moment of inertia method can be used to calculate the stiffness of composite strengthened beams subjected to fatigue loading. theoretical calculation results are in good agreement with the experimental results.

References

[1] AL-ROUSAN R, ISSA M. Fatigue performance of reinforced concrete beams strengthened with CFRP sheets [J]. Construction and Building Materials, 2011, 25(8): 3520-3529.

[2] FERRIER E, BIGAUD D, CLMENT J C, HAMELIN P. Fatigue-loading effect on RC beams strengthened with externally bonded FRP [J]. Construction and Building Materials, 2011, 25(2): 539-546.

[3] OUDAH F, EL-HACHA R. Research progress on the fatigue performance of RC beams strengthened in flexure using fiber reinforced polymers [J].Composites Part B: Engineering, 2013, 47(4): 82-95.

[4] DONG J F, WANG Q Y, GUAN Z W. Structural behaviour of RC beams externally strengthened with FRP sheets under fatigue and monotonic loading [J]. Engineering Structures, 2012, 41(8): 24-33.

[5] WANG Su-yan, WANG Ze-yuan. Mechanism of improving ductility of high strength concrete T-section confined by CFRP sheet subjected to flexural loading [J]. Journal of Central South University, 2013, 20(1): 246-255.

[6] CERONI F. Experimental performances of RC Beams strengthened with FRP materials [J]. Construction and Building Materials, 2010, 24(9): 1547-1559.

[7] OUDAH F, EL-HACHA R. A new ductility model of reinforced concrete beams strengthened using fiber reinforced polymer reinforcement [J]. Composites Part B: Engineering, 2012, 43(8): 3338-3347.

[8] CERONI F, PECCE M, MATTHYS S, TAERWE L. Debonding strength and anchorage devices for reinforced concrete elements strengthened with FRP sheets [J]. Composites Part B: Engineering, 2008, 39(3): 429-441.

[9] ARSLAN G, SEVUK F, EKIZ I. Steel plate contribution to load-carrying capacity of retrofitted RC beams [J]. Construction and Building Materials, 2008, 22(3): 143-153.

[10] LEI Dong, CHEN Guang-yuan, CHEN Yu-quan, REN Qing-wen. Experimental research and numerical simulation of RC beams strengthened with bonded steel plates [J]. Science China Technological Sciences, 2012, 55(12): 3270-3277.

[11] AYKAC S, KALKAN I, AYKAC B, KARAHAN S, KAYAR S. Strengthening and repair of reinforced concrete beams using external steel plates [J]. Journal of Structural Engineering, 2013, 139(6): 929-939.

[12] LU Yi-yan, ZHOU Ting, ZHAO Guo-fan. Calculation analysis of resisting flexural strength of RC beams strengthened by combination of CFRP and steel plate [J]. Journal of Hydroelectric Engineering, 2006, 25(3): 77-83. (in Chinese)

[13] LU Yi-yan, ZHOU Ting, ZHANG Wei. Ductility analysis of RC beams strengthened with carbon fiber reinforced polymer and steel plate [J]. Journal of Harbin Institute of Technology, 2006, 38(11): 1939-1942. (in Chinese)

[14] LU Yi-yan, ZHOU Ting. Experimental research on flexural performance of reinforced concrete beams combination strengthened with bonded carbon fiber reinforced polymer and steel plates [J]. Journal of the China Railway Society, 2006, 28(1): 80-87. (in Chinese)

[15] LU Yi-yan, ZHOU Ting. Calculation of sectional stiffness of RC beams combination strengthened with CFRP and steel plates [J]. Journal of the China Railway Society, 2007, 29(1): 72-76. (in Chinese)

[16] GUO Zhen-hai. Theories of reinforced concrete [M]. 3rd ed. Beijing: Tsinghua University Press, 2013. (in Chinese)

[17] BALAGURU P N, SHAH S P. A method of predicting crack widths and deflections for fatigue loading [J]. ACI Special Publication, 1982, 75: 153-175.

[18] ACI Committee 318-08. Building code requirements for structural concrete [S]. American Concrete Institute, 2008: 107-123.

[19] PAPAKONSTANTINOU C G, BALAGURU P N, PETROU M F. Analysis of reinforced concrete beams strengthened with composites subjected to fatigue loading [J]. ACI Special Publication, 2002, 206: 1-17.

(Edited by YANG Hua)

Foundation item: Project(51108355) supported by the National Natural Science Foundation of China; Project(2011CDB269) supported by the Natural Science Foundation of Hubei Province, China

Received date: 2015-01-21; Accepted date: 2015-06-11

Corresponding author: LU Yi-yan, Professor, PhD; Tel: +86-27-68775832; E-mail: yylu901@163.com