Modification of computer simulation of normal grain growth
LI Jian(李 剑), LI Shi-chen(李世晨), ZHENG Zi-qiao(郑子樵),
LIU Zu-yao(刘祖耀), CHEN Da-qin(陈大钦)
(School of Materials Science and Engineering, Central South University, Changsha 410083, China)
Abstract: A set of principles on transition probability was supplied for the physical process of grain growth. In accord with these principles, a modified transition probability considering the influence of temperature was put forward to simulate the normal grain growth relying on temperature and second phase particles. The modified transition probability correctly reflects the dependence of grain growth on the temperature. The effect of different shapes of second phase particles on the grain growth process was taken into account using the modified transition probability. The relationship between the area fraction of second phase particles and the limit of grain size of the matrix was given. The microstructural evolution patterns employed to 2-D were given. The results agree well with the real grain growth process. All these suggest that the modified transition probability is better than the conventional one.
Key words: transition probability; normal grain growth; Monte Carlo method; computer simulation CLC number: TG111.7; TP991.9
Document code: A
1 INTRODUCTION
The normal grain growth is one of the most important microstructural evolution processes during the annealing of metals. In this process, some changes of configuration take place, including the grain size and its distributions, stability of grains, and the topological characteristics formed by grains. All these changes have great influence on the mechanical properties of metals when they are fabricated and put into use. Therefore, it has being studied by many researchers. It is promising to take an effective control over this process and then control the properties of metals. With the progress of computational technology, some computing simulation methods have been developed. Among all of these different methods, Monte Carlo Method is a classical one[1-11]. Monte Carlo Method was first employed in the 2-D computer simulation of this process by Anderson et al[12] through the Potts model. Then, the normal grain growth pinned by the second phase particles were simulated in three dimensions[13]. This model was also employed to the grain growth in thin films by Frost et al[14].
But there are still some problems in those simulating works. The main problem in these models is that the influence of temperature on the process cannot be taken into account, and then simulation temperature is too low, which is not accord with the real process. In this paper, some modification on the problem will be tried and employed to the normal grain growth of single-phase alloy and that pinned by the second phase particles. The simulation results are more reasonable.
2 LIMITATION OF EXISTING TRANSITION PROBABILITY AND ITS MODIFICATION
2.1 MC grain growth algorithm
The Potts model is frequently used in the computer simulation of the grain growth process, the algorithm is shown as follows.
1) A simulation domain of a suitable size(256×256) is chosen.
2) Using the assumption of ‘coarsening grains’, the microstructure can be discretely characterized by an array of discrete grids.
3) Every grid was randomly assigned a random number Sj between 1 and NQ, where NQ is the total number of grain orientations. In this simulation, NQ is chosen to be 64. A grain is defined by a collection of the points, which have the same orientation number without the interruption of other numbers.
4) The grid was randomly chosen and the orientation was changed to another different random number between 1 and NQ. Energy change of this reorientation is calculated, which only takes the nearest neighbors into account. And the result was substituted to the expression of the transition probability and a number ranging between 0 and 1 is derived. Then, generating another random number and comparing this number with the number derived above, the possibility of the acceptance of the reorientation can be determined. That is, if the latter is larger than the generated number, the reorientation is accepted and vice verse.
5) The operation 4 was employed to all of the grids and a Monte Carlo Step is counted.
6) Repeating the operation 2 to 5 until the required Monte Carlo Step needed is completed.
2.2 Problem
In the algorithm shown above, the key step is the change of the orientation. In this step, the transition probability strongly depends on the transition probability. In the classical simulation, the expression of the transition probability[11] is shown as
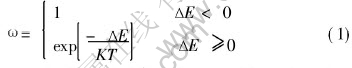
where ω is the probability of successful reorientation, ΔE is the energy change due to the reorientation, K is the Boltzmann constant, T is the absolute temperature.
From Eqn.(1), it can be shown that when the value of energy change is lower than 0, the transition probability is equal to 1 that means, if the thermodynamics is favored, the configuration transfer is accepted automatically. The conclusion is not completely correct. So Eqn.(1) is not reasonable. The main points associated with the weakness of Eqn.(1) are as follows. 1) The problem of temperature, that is, if the value of energy difference of the orientation change is negative, the normal grain growth would be uncorrelated with the temperature. This is not accord with the fact that the grain growth strongly depends on the temperature. 2) The problem at the point ΔE=0. When the value of energy difference is 0, the transition probability is 1, that is, if the system is at an equilibrium state, the normal grain growth phenomenon also takes place.
To solve the problems existing in the transition probability, the Symmetrical probability is used[10], and the expression is shown as
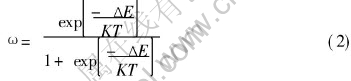
This probability solves the problem at the point ΔE=0 to some extent. But from Eqn.(2), it can be seen that when ΔE is lower than 0, ω can not be higher than 0. So there is a conflict between the simulating result and the real process of grain growth.
2.3 Modified transition probability
It is important to give an appropriate transition probability, which can be used to characterise the physical process. When the thermodynamics and some basic laws on the real grain growth are taken into account, there is a set of principles expressed mathematically as below, which should be satisfied in the real process of normal grain growth.
1) There is a specific temperature designated as TR. When the temperature is higher than TR. The probability is 1/2;

To get the analytical expression of the transition probability, the condition (1) can be broadened as follows.
There is a physical parameter TR. When the temperature T is equal to TR,the probability ω(T=TR, ΔE=0) is 1/2. But when the temperature T is higher than TR,the probability ω(T, ΔE=0) is at the vicinity of 1/2.
Based on the conditions the probability requires, the Eqn.(3) can be fitted as
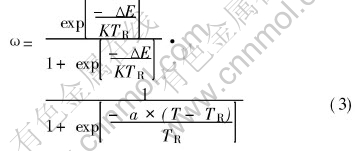
where ΔE is the energy difference, TR is the temperature of recrystallization as to the specific alloy system, a is a fitted factor which can be gained by the condition (1)′. Eqn.(3) reflects the relation among the thermodynamics, dynamics and temperature. When the specific temperature TR is 673K, a is 15, the curve of Eqn.(3) with different simulation temperatures is shown in Fig.1.
3 NORMAL GRAIN GROWTH IN SINGLE-PHASE ALLOY
The simplest grain growth process is the normal grain growth in single-phase alloy. Then, applying the modified transition probability to the normal grain growth in single-phase alloy, the influence of temperature on the grain growth dynamics and size distribution can be tested.

Fig.1 Curves of modified transition probability
Temperature is an important factor that affects the process of recrystallization and grain growth in metals. The results of the single-phase alloy derived from the modified transition probability are shown in Fig.2(a). From the figure, it can be seen that the temperature has a strong effect on the process of grain growth. When the temperature is lower than 273K, the value of average grain size almost keeps as a constant. The higher the temperature, the larger the average grain size becomes. When the temperature is higher than 673K, the effect of temperature on the growth of individual grain is almost the same, and the average grain size also becomes invariable. Then, it can be seen that using the modified transition probability, the simulation results agree well with the theoretical analysis and physical process. Fig.2(b) shows the results derived from the conventional probability. Compared with Fig.2(a), it suggests that the conventional probability cannot correctly reflect the dependence of the grain growth on the temperature. There is not significant difference of the grain growth at the temperature 273K and 773K. It is strange that the average grain size at 673K is much lager than the one at 773K. This is not in accordance with the experimental results.
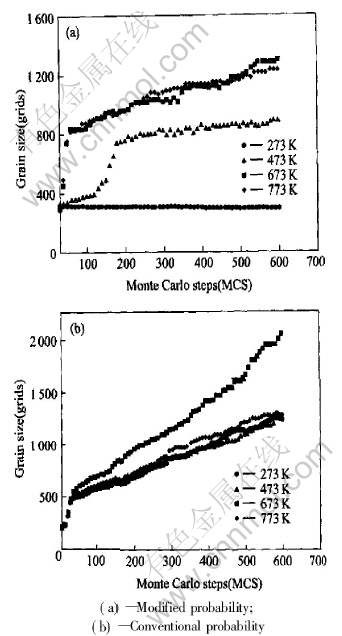
Fig.2 Grain growth kinetic curves at different temperatures
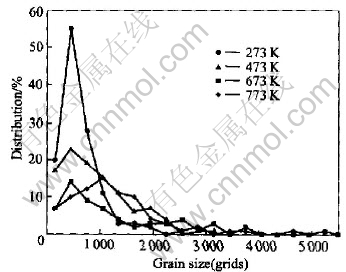
Fig.3 Grain size distributions at different temperatures
Fig.3 shows the grain size distributions after simulated for 600 MCS with the variation of temperature. It suggests that in the lower temperature range, the distribution is stiff, that is, the grain size with the most frequent probability is at the end of the lower limit along the axis of the grain size. As temperature becomes higher, the mobility of grain boundaries also increases. Then, the large grains become larger, while the small grains become smaller and disappear in the end. The average grain size increases and the size distribution becomes broader and smoother. When the temperature is higher than 673K, the effect of temperature on the distribution of grain size becomes weaker. From the Fig.3, it can be seen that the grain size of peak value becomes larger as the temperature increases. This is coinciding with the physical process. Then, it can be concluded that the modified transition probability can be used in the computer simulation.
4 NORMAL GRAIN GROWTH PINNED BY SECOND PHASE PARTICLES
4.1 Effect of fraction of second phase particles
Using the modified transition probability, the computer simulation results with the variation of area fraction are shown in Fig.4. It is demonstrated that the average grain size decreases with the increase of the area fraction of second phase particles. It can be illustrated that the dispersed and fine particles inhibit the movement of the grain boundary and thus weaken the tendency of grain growth, making the size distribution uniform. This is consistent with the results that the second phase particles can refine the grains in the multiphase systems.
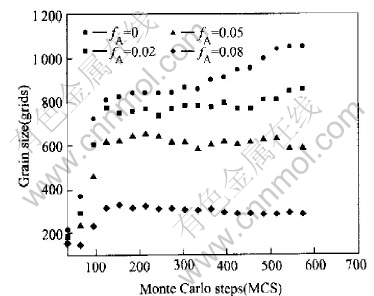
Fig.4 Grain growth kinetic curve for different fA
4.2 Effect of shape of second phase particles on grain growth
Fig.5 shows the average grain size change with the variation of the particle shapes. With the quantitative analysis, it can be seen that under the same conditions, when the area fraction of second phase particles is small, the limit of the average grain size in the microstructure pinned by needle particles is lower than that of the microstructure pinned by spherical particles. But this phenomenon becomes weaker as the fraction increases.
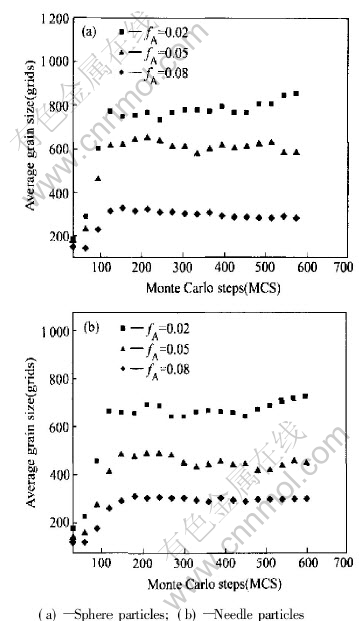
Fig.5 Grain growth kinetic curves for different fA
The relations among the size of second phase particles, the area fraction of the particles and the limit of the average grain size of the matrix, can be expressed as[15]

where Rlim is the limit of the average grain size, r is the radius of the particles, fA is the area fraction of the second phase particles, both CP and np are constants, the determination of np is the most important factor. With the logarithmic transformations on both sides of the equation shown above, the Eqn.(4) can be expressed as below:
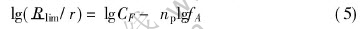
Fitting the data derived from Fig.4 and Fig.5(shown in Fig.6), with the least square method, the results as follows.
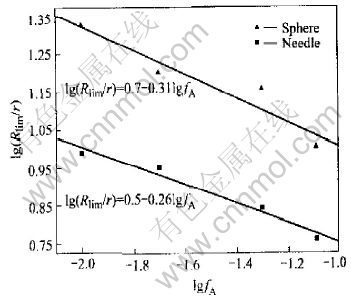
Fig.6 Relationship between lg(Rlim/r) and lgfA

It can be seen from the Eqns.(8), (9) that the effect of microstructure pinned by needle particles is stronger than that of the microstructure pinned by sphere particles. Comparing the results with the results in the literature[12, 13], it can be seen that the former are consistent with the latter.
Fig.7 shows the dependence of the microstructure on the shapes and area fraction of second phase particles. From Figs.6 and 7, it can be concluded as follows.
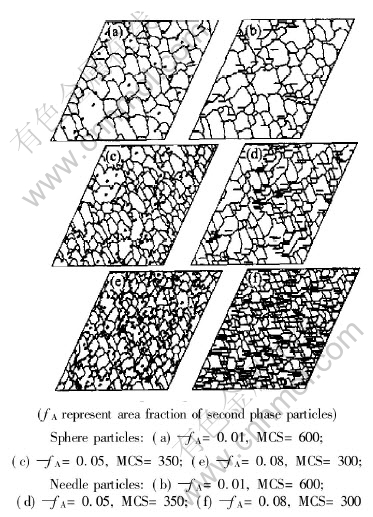
Fig.7 Microstructure evolution patterns pinned by different volume fractions of second phase particles
1) As the fraction increases, the limit of average grain size of the matrix decreases and the distribution becomes uniform.
2) At the same fraction and sizes, the microstructure pinned by the needle particles is more stable than that pinned by sphere particles,so the refinement effect of needle particles better than that of sphere particles. From the topological geometrical point of view, it can be illustrated as: 1) When the area fraction of the needle particles is too small, the grain boundaries topologically contact with the second phase particles at some points and the effect of needle particles on the microstructural evolution is the same as that of sphere particles; 2) As the area fraction of second phase particles increases, line-contact becomes the most frequent topological way of the contact between the grain boundaries and second phase particles, the growth speed normal to the plate of the needle particles is inhibited, so the grains of particles become preferentially oriented.
Fig.8 shows the simulation results relating to the fraction of the grain size distributions. When the fraction increases, the distribution becomes broader, while the value of the peak increases. It can be interpreted that the dispersed, fine particles strongly inhibit the movement of the grain boundary and weaken the tendency of grain growth, making the size distribution broader. Comparing the data derived from the two shapes, it can be seen that the size distribution of needle shapes is much stiffer and the peak values are much higher. The effect of needle particles on the microstructure is stronger than that of sphere particles.
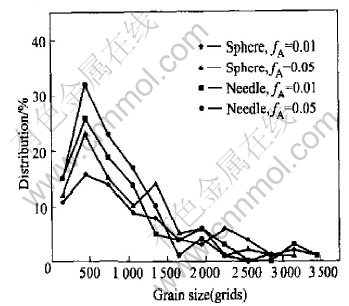
Fig.8 Grain size distributions at grain growth stagnation for different fA
5 CONCLUSIONS
1) Using Monte Carlo method, the modified transition probability is applied to the normal grain growth process in single-phase alloys. Comparing the results with the classical results, it can be seen that the grain growth speed increases sharply as the temperature increases to a definite value, but at low temperature, the growth process does not take place. So the modified transition probability considering the effect of temperature can reasonably reflect the physical process of normal grain growth.
2) The modified transition probability is applied to the normal grain growth process pinned by second phase particles.

② When the area fraction of second phase particles is low, the grain size pinned by needle particles is much smaller than that pinned by sphere particles in the 2-D simulation. As the area fraction increases, the shape effect on the grain size limit becomes weaker while the effect on the morphology becomes stronger.
③ When the second phase particle is needlelike, the size distribution of the matrix is broader than that of sphere particles.
REFERENCES
[1]Svolovitz D J, Anderson M P, Grest G S, et al. Grain growth in two dimention [J]. Scripta Metal, 1983, 17(2): 241-246.
[2]Srolovitz D J, Anderson M P, Grest G S, et al. Computer simulation of grain growth(Ⅲ)—Influence of a particle dispersion [J]. Acta Metal, 1984, 32(9):1429-1438.
[3]Srolovitz D J, Grest G S, Anerson M P. Computer simulation of grain growth(Ⅴ)—Abnormal grain growth [J]. Acta Metall, 1985, 33(12): 2233-2247.
[4]Grest G S, Srolovitz D J, Anderson M P. Computer simulation of grain growth(Ⅳ)—Anisotropic grain boundary energies [J]. Acta Metall, 1985, 33(3): 509-520.
[5]Atkinson H V. Theories of normal grain growth in pure single phase systems [J]. Acta Metal, 1988, 36(3): 469-491.
[6]Rollett A D, Srolovitz D J, Anderson M P. Simulation and theory of abnormal grain growth—Anisotropic grain boundary energies and mobilities [J]. Acta Metall, 1989, 37(4): 1227-1240.
[7]Toshiya S, Hideaki T, Shigenori H. Monte Carlo simulation for the behavior of low mobility grain boundaries in grain growth [J]. Materials Transactions JIM, 1991, 32(1): 25-31.
[8]Saito Y, Enomoto M. Monte Carlo simulation of grain growth [J]. ISIJ(The Iron and Steel Institute of Japan) International, 1992, 32(3): 267-274.
[9]GAO Jin-hua, Thompson R G, Patterson B R. Computer simulation of grain growth with second phase particle pinning [J]. Acta Metal, 1997, 45(9): 3653-3658.
[10]Binder K. Methods in Statistical Physics [M]. Berlin Heidelberg: Springer, 1986.
[11]ZHONG Xiao-zheng, CHEN Wei-yuan, WANG Hao-cai, et al. Computer simulation of grain growth in polycrystalline materials(Ⅰ)—Normal grain growth [J]. Functional Materials, 1999, 30(3), 232-235.(in Chinese)
[12]Anderson M P, Srolovitz D J, Grest G S, et al. Computer simulation of grain growth(Ⅰ)—Kinetics [J]. Acta Metal, 1984, 32(5): 783-791.
[13]Anderson M P, Grest G S, Doherty R D, et al. Inhibition of grain growth by second phase particles:three dimensional Monte Carlo computer simulation [J]. Script Metal, 1989, 32(5): 753-758.
[14]Frost H J, Thompson C V, Walton D T. Simulation of thin film grain structures(Ⅰ)—Grain growth stagnation [J]. Acta Metall Mater, 1990, 38(8): 1455-1462.
[15]SONG Xiao-yan, GU Nan-ju, LIU Guo-quan, et al. Computer simulation of the influence of second-phase particle quantity on matrix grain growth [J]. Acta Metal Sin, 2000, 36(6): 592-596.(in Chinese)
(Edited by LONG Huai-zhong)
Foundation item: Project(59971066) supported by the National Natural Science Foundation of China
Received date: 2004-05-09; Accepted date: 2004-09-10
Correspondence: ZHENG Zi-qiao, Professor; Tel: +86-731-8830270; E-mail: s-maloy@mail.csu.edu.cn