J. Cent. South Univ. (2020) 27: 2776-2791

DOI: https://doi.org/10.1007/s11771-020-4498-4

Dynamic performance of six-axle locomotive subjected to asymmetric brake shoe forces

LIU Peng-fei(刘鹏飞)^{1, 2}, ZHANG Kai-long(张凯龙)², CAO Yun-qiang(曹云强)²

1. State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;

2. School of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China

Central South University Press and Springer-Verlag GmbH Germany,part of Springer Nature 2020

Abstract: To research the influence of asymmetric brake shoe forces(ABSF) induced by braking failure on the dynamic performance of six-axle locomotive, the static equilibrium model of three-axle bogie and dynamic model for locomotive are established. The coupling vibration equations of axle hung motor and wheelset are derived. For the air braking, the influence mechanism of ABSF on the wheel-rail asymmetric motion and force characteristics are discussed. It can be found that if the ABSF is applied in the front wheelset, all the wheelsets move laterally in the same direction. Once the ABSF occurs in the middle or rear one, other wheelsets may move laterally towards the opposite direction. The motion amplitude and direction of all wheelsets strictly depend on the resultant moment of suspension yawing moment and brake shoe asymmetric moment. For the asymmetric braking, the free lateral gap of axle-box could increase the wheelset motion amplitude, but could not change the moving direction. In both the straight line and curve, the ABSF may lead to wheelset misaligning motion, intensify the wheel-rail lateral dynamic interaction and deteriorate wheel-rail contact state. Especially for the steering wheelsets, the asymmetric braking increases the wheelset attack angle significantly, which forms the worst braking condition.

Key words: locomotive; brake shoe force; dynamic performance; asymmetric braking; wheel-rail contact

Cite this article as: LIU Peng-fei, ZHANG Kai-long, CAO Yun-qiang. Dynamic performance of six-axle locomotive subjected to asymmetric brake shoe forces [J]. Journal of Central South University, 2020, 27(9): 2776-2791. DOI: https://doi.org/10.1007/s11771-020-4498-4.

1 Introduction

The foundation brake rigging is an important component in the locomotive which is generally equipped with the unit brake. However, the braking failure has been a noticeable problem in the vehicle maintenance. For the six-axle locomotive of HXD, the failures of brake shoe seizure occurred 9 times within one year from March, 2013 to April, 2014, the brake unit has to be replaced and even the wheels need to be repaired [1]. Earlier in 2004, it was reported that 7 braking units in 5 locomotives of DF8B failed without braking shoe forces [2]. The suspended connecting rod of unit brake in locomotive even fractured in some special cases, which affected the normal brake application [3]. The wheel-rail degraded adhesion issue in braking maneuver and its corresponding quantification method were studied by BOSSO et al [4]. Whether the brakes shoe seizure or brake force loss, they represent the typical faults in the brake system. It may shorten the service time of brake elements and threaten locomotive running safety in some extreme conditions. For the issues mentioned, DURALI et al [5] investigated train running safety in emergency braking and found that the brake could lead to the increase of derailment coefficient. HANDOKO et al [6] discussed the dynamic influence of asymmetric brake shoe forces on curving negotiation of wagon, and found that the asymmetric force could increase the wheelset attack angle and wheel-rail lateral forces. BELFORTE [7] and PUGI et al [8] focused on the dynamic performance of train passing through switch sections under the braking conditions, and it was found the emergency braking posed threats to the train running safety. By introducing the safety evaluation criterion of railway train, WILSON et al [9] believed the assessment in emergency braking is an extreme condition, which could cause the increase of wheel-rail lateral force and ought to be evaluated as the special cases. ZHANG et al [10] found that the brake moment in wheelset induced the significant wheel-load reduction rate if the track lateral irregularity was considered. FENG [11] pointed out that the lateral displacement of brake beam could induce the significant difference for different brake shoe forces, which was the main reason resulting in the uneven wear of brake shoes. LIU et al [12-14] developed a train-track coupled dynamic model and studied the train running safety on straight line and sharp curves in braking conditions. Recently, WU et al [15] and SHRESTHA et al [16] studied the modeling method of traditional air brake system and discussed the control algorithm for optimum utilization of the available adhesion between wheel and rail in braking conditions. GUNAY et al [17] compared and analyzed the characteristics of adhesion dependent and independent brakes. Based on the bench test, MAZZU et al [18] researched the influence of shoe braking and wheel-rail rolling- sliding contact on the wheel wear and fatigue. WANG et al [3] found that the axial force, lateral friction force and braking force are the dominant factors leading to the fracture problem of suspended rod in unit brake. XIE et al [19] found that the main reason of brake shoe eccentric wear could be attributed to the overshoot in the installation seat of unit brake. For the two-axle bogie, LIU et al [20] discussed the influence of unbalanced brake shoe forces on dynamic behavior of front and rear wheelsets for traditional two-axle bogie. The relevant researches mentioned above mainly focus on the dynamic performance of vehicle with four axles in braking conditions, no matter the braking device works in normal or failing state. However, the six-axle locomotive has its particularity, i.e. the axle arrangement as well as the nonlinearities in axle-box suspension is significantly different from that of B0-B0 locomotive. Quite a number of braking device failures have occurred in the C0-C0 locomotive as reported in Refs. [1-3]. Also, in the on-site survey, the wheel tread continuous spalling and incomplete contact of brake shoe have been observed, as shown in Figure 1. What is the effect of asymmetric brake forces or whether these phenomena are related with the asymmetric braking? It is an important issue needing urgent attention.

The asymmetric brake shoe forces (ABSF) on both sides of the wheelset have an adverse effect on the braking capacity, and also form an additional yawing moment for the wheelset, which is called as the brake shoe asymmetric torque (BSAT) in this paper. The dynamic behavior of wheelset strictly depends on the creep forces and suspension forces. Once the BSAT occurs, the issue how the wheelset motion and wheel-rail contact states change has not yet been focused widely and discussed in depth. It is significant for the train running safety and braking system maintenance by understanding the action mechanism and dynamic influence laws of BSAT. For this purpose, taking a three-axle bogie as an example firstly, its linear mechanical model with 8 degrees of freedom (DOFs) is established and the corresponding equilibrium equations are given. The action mechanism of BSAT is studied. For the different brake shoe forces and BSATs in straight line and curves, the wheelset behaviors and wheel- rail dynamic interaction are investigated by a three- dimensional locomotive dynamic model, which takes the nonlinear properties into account.

Figure 1 Structure of three-axle bogie in heavy-haul locomotive:

2 Equilibrium equation of locomotive bogie under ABSF

To clarify the problem clearly, an elastic constraint wheelset is introduced firstly to reveal the force conditions and action process under the asymmetric brake shoe forces, as shown in Figure 2. It is assumed that the right brake unit fails and the left one works well. So the left and right brake shoe forces satisfy the relation of F_BL>F_BR, which results in a yaw torque (BSAT) driving the wheelset to rotate along the clockwise direction. A positive yaw angle of wheelset j_w forms. Based on the wheel-rail creep theory, the wheel-rail lateral creep force and yaw angle meet the relation in formula (1). As a result, a positive lateral creep force F_y produces in the wheel-rail contact surface. A corresponding positive lateral movement y_w occurs, which results in a pair of opposite longitudinal creep forces (F_Lx, F_Rx) acting in the left and right wheels as shown in Figure 2. Their specific values can be calculated in formula (2). It should be noted that the resultant yaw moment induced by longitudinal creep forces is opposite to the BSAT direction. The wheelset must move laterally to produce enough yaw angle until the suspension restoring forces and resultant creep moment combine to balance the BSAT, so that a new equilibrium state is obtained.

F_y=2f₂₂·φ_w                                        (1)

                   (2)

where f₁₁ and f₂₂ are the longitudinal and lateral creep coefficients, respectively; λ and r₀ denote the tread conicity and wheel radius, respectively.

Figure 2 Motion of single wheelset under ABSF

For a multi-axle bogie, the similar mechanical process may occur in different wheelsets. However, whether the acting effects obey the same rules is an outstanding issue. To illustrate the essence and highlight the wheelset creep steering abilities, a typical three-axle bogie (Figure 3) is taken as the research object, in which only the lateral and yawing DOFs for bogie frame and wheelsets are considered. F_B(L,R)i represents the brake shoe forces in the left and right wheels of the ith wheelset. Other structure and suspension parameters are listed in Table 1. For the static equilibrium analysis, the damping effect and vibration velocity items in the system are ignored.

To reflect the basic motion attitude of bogie in its equilibrium position under ABSF, the assumption of small displacement for wheelset is introduced so that the motion equations can be linearized. Accordingly, the bogie static equilibrium equations can be derived easily. Eqs. (3) and (4) represent the lateral and yaw equilibrium equations of bogie frame, and Eqs. (5)-(8) are the lateral and yaw equilibrium equations of the three wheelsets.

Figure 3 Static equilibrium model of typical three-axle bogie

Table 1 Parameters for bogie static equilibrium model

        (3)

                        (4)

            (5)

                (6)

            (7)

         (8)

where k_pj and k_sj are the anti-yaw stiffness of primary and secondary suspensions; M_i denotes the BSAT of the ith axle; j_t is the yaw angle of bogie frame. The calculation of these parameters can be expressed as

                             (9)

                            (10)

                      (11)

Equations (3)-(8) are the typical linear equations which can be solved by the Gauss-Jordan elimination method conveniently. The running behaviors of different wheelsets under the steady BSAT are then obtained.

3 Asymmetric motions of different wheelsets under BSAT

For the same BSAT, whether does it have the same effect on different wheelset? If the bogie frame is regarded as the fixed boundary, the wheelsets in different positions of bogie will have independent motions and obey the same motion law according to the model in Figure 2. Actually, the wheelsets may coordinate their mutual motion relations by the bogie frame. Based on the bogie static equilibrium model in Figure 3, the wheelset motion attitudes are investigated by assuming the right brake element of the 1st, 2nd and 3rd wheelsets fails in sequence. Three cases discussed are listed in Table 2.

Table 2 Cases of brake element failure for bogie

For the three cases, the lateral movements and motion attitudes of bogie components are compared in Figure 4, where BF, W1, W2 and W3 represent the bogie frame, 1st, 2nd and 3rd wheelsets in sequence. It shows that there are clear differences between the calculated results in cases 1-3, which means the BSAT in different wheelsets may lead to the complicated misaligning motions of wheelsets. Viewed from the cover range of bogie lateral displacement, for example in Case 1, W1 and W3 have the lateral shifts of 4.2 and 1.4 mm, respectively, corresponding to the maximum and minimum values. In Case 2, the range is from -0.8 mm of W1 to 2.0 mm of W2. However, in Case 3, the lateral displacement bounds are changed to -2.9 and 0.54 mm, occurring in W1 and W3 respectively. Without exception, the wheelset has a positive displacement if it is subjected to a clockwise BSAT, which depends on the creep steering ability as explained in Section 1. The maximum absolute displacement in Case 1 is about 2.1 times and 1.45 times the values in Cases 2 and 3.

Figure 4 Wheelset motions under clockwise BSAT:

Obviously, the BSAT has the significant influence on the lateral motion of first wheelset. From the aspect of yawing motion, the yaw angles of wheelset 1 in Case 1, wheelset 2 in Case 2 and wheelset 3 in Case 3 respectively reach 0.19×10^-3, 0.19×10^-3 and 0.14×10^-3 rad. Therefore, although the three wheelsets bearing the same BSAT in three cases have the similar yaw angles, they still present very different lateral behaviors.

A obvious phenomenon is found that, the influence rules of BSAT on wheelset 1 and 3 has the asymmetric characteristics. So which factor determines the specific movements of wheelset, should be discovered in depth. Equation (8) can be transformed to Eq. (12). It is clear that the wheelset lateral displacement totally depends on the resultant moment of M_ji and M_i.

                (12)

where M_ji represents the suspension yaw moment.

Introduce the resultant moment M_resi, which can be expressed as:

                         (13)

To reveal the motion rules in Figure 4 as a clear formation, M_resi values in different cases are calculated, and the relations between M_resi and wheelset lateral moving direction are given in Figure 5. For M_resi>0, the wheelset has a positive lateral displacment. Otherwise, it moves towards the negative direction. Without doubt, the larger M_resi may lead to larger lateral displacement, which is in accordance with the motion characteristics in Figure 4(a).

Figure 5 Relations between M_resi and wheelset lateral moving direction

Let us discuss the influence and mechanism of BSAT deeply. In Case 1, if a clockwise BSAT is applied in the first axle, the wheelset will yaw clockwise and induce the lateral creep forces to drive the wheelset moving laterally and positively. Both the wheelset yaw and lateral motions can also cause the bogie frame to yaw clockwise as shown in Figure 4(b), which means that the wheelset and bogie frame have the yaw angles (j_w1 and j_t) with the same direction. Affected by this, the suspension yaw torque M_ji is reduced significantly so that its influence on wheelset motion is minimized. By Eq. (9), the BSAT M_i becomes the main factor driving the wheelset to move positively with a large amplitude. In other words, only a large lateral displacement of the wheelset can produce enough longitudinal creep forces to balance the outer BSAT.

For the middle wheelset in Case 2, j_t and j_w2 have the inverse signs as shown in Figure 4(b), which denotes the resultant M_ji increases negatively and balance a part of positive M_i. Therefore, the residual M_i also can drive wheelset 2 to move but with a relatively small positive displacement. For the rear wheelset under the clockwise BSAT in Case 3, it yaws clockwise (positive value) and moves towards the positive direction, which drives the bogie frame to produce a large negative yaw angle as shown in Figure 4(b). The difference of j_t and j_w3 increases negatively. Finally, the anticlockwise suspension moment M_ji increases and effectively balances the BSAT M₃, so that the value of resultant M_res3 decreases. The rear wheelset could only move with a smaller lateral displacement according to Eq. (12). That is why the three wheelsets behave differently if the same BSAT is applied in them respectively.

4 Wheelset dynamic behaviors in nonlinear locomotive system

The general laws obtained above are based on the assumption of the linearized vehicle system. To accurately reflect the actual states of locomotive and examine the analysis results under BSAT, it is necessary to carry out the research as the relevant nonlinear characteristics of the wheel-rail contact and suspension parameters are taken into account. The multi-rigid modeling method has been utilized widely in the locomotive simulation and locomotive-track coupled model [21], but the wheelset-motor unit has some special characteristics distinct from the other components. For the maintenance convenience of heavy-haul locomotive, the axle-suspend motor is usually installed on the wheelset by the axle suspension bearings, which means there exists the rigid constraints between the axle and motor. The motor only has independent pitching motion relative to the wheelset, while other DOF motions couple with that of wheelset. Comparatively, both the carbody and bogie frame have 6-DOFs independent motions. Considering the effect of BSAT and the axle-suspend characteristic of traction motor simultaneously, the coupling motion equations of wheelset-motor subsystem are given below. The force states are shown in Figure 6.

The longitudinal (X_w), lateral (Y_w), vertical (Z_w), side rolling (φ_w), pitching (β_w) and yawing (ψ_w) motion equations of wheelset can be expressed as

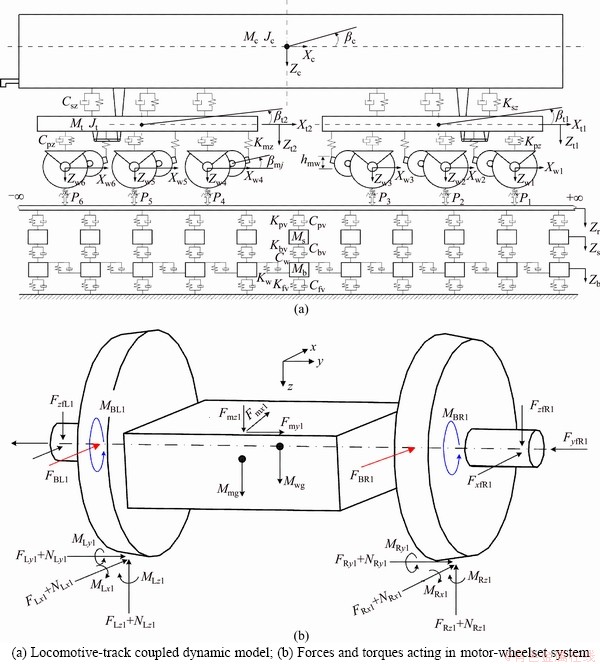
Figure 6 Locomotive dynamic model:

where i =1-6 denotes the 1st to 6th axle; n=1, 2 is the front and rear bogie; g is the gravity acceleration; M_BLi and M_BRi are the braking torques in the left and right wheels; F_Lxi and F_Rxi represent the longitudinal creep forces in left and right wheels; F_Lyi and F_Ryi are the left and right lateral creep forces; F_Lzi and F_Rzi are the vertical components of the left and right creep forces in sequence; N_Lxi, N_Lyi and N_Lzi denote the longitudinal, lateral and vertical components of left normal force, while N_Rxi, N_Ryi and N_Rzi represent the corresponding forces in the right wheel; F_xfLi, F_yfLi and F_zfLi are the left primary suspension forces in x, y and z directions, and F_xfRi, F_yfRi and F_zfRi denote the right suspension forces; M_Lxi, M_Lyi and M_Lzi are the left components of creep moment in x, y and z directions; M_Rxi, M_Ryi and M_Rzi are the right components of creep moment in x, y and z directions; F_mxi, F_myi and F_mzi represent the longitudinal, lateral and vertical forces of the motor suspension; r_Li and r_Ri are the left and right wheel rolling radii in order; R_wi and f_sewi are the curve radius and super elevation angle of outer rail for the ith wheelset; Ω is the nominal running speed; l₁ and l₂ are the distances from motor mass center to wheelset and suspending point respectively.

Then, the coupling vibration equation of driving motor can be expressed as:

To verify the asymmetric motions presented in Section 2, some typical nonlinear parameters are included in the entire locomotive dynamic model. For the wheel-rail contact geometries, both the cone wheel profile with constant conicity of 0.075 and Jm3 profile with nonlinear conicity are taken into account, as shown in Figure 7. For the calculation of wheel-rail forces, the wheel-rail spatial dynamic interaction model is used, which has been discussed deeply in Refs. [12, 13, 21] and will not be explained here. Specially, the wheel-rail tangential forces are calculated by the classic Fastsim which could reflect both the wheel-rail adhesion and sliding phenomena in the real-time simulation.

It should be noted that some structure particularities exist in the design of middle axle-box. The wheelset can move freely within a small lateral gap, which is helpful to improve the steering ability of middle wheelset in curved track. As given in Figure 8(a), the free lateral gap δ is obtained by the cylindrical roller bearing, while the longitudinal and vertical relative motions between axle and axle-box are limited by the bearing structure. Only if the relative lateral displacement of middle axle exceeds the range δ, the primary suspension could deform and produce certain lateral force to restrict the wheelset further movement. Otherwise, there is no lateral spring-damping force in the primary suspension. The specific mechanical property is shown in Figure 8(b).

Figure 7 Wheel profiles and equivalent conicity

In Case 1, assuming that the lateral free gap has two possibilities of 0 and 15 mm, the dynamic responses of wheelsets are shown in Figure 9. Comparing with the results in Figure 4(a), the lateral displacements of 1st to 3rd wheelsets for δ= 0 mm can reach 3.23, 1.29 and 1.28 mm, which indicates the wheelsets have the similar motion magnitudes and the same moving direction. Also the wheelset yaw angles have no exceptions. However, once the wheelset free lateral gap is considered, the 1st and 3rd wheelsets present larger lateral displacements under the BSAT in Case 1.

Figure 8 Nonlinear suspension property between axle-box and middle wheelset:

Figure 9 Wheelset displacements in Case 1 with and without free lateral gap:

Further, the lateral displacements of three wheelsets are compared in Figure 10. In all cases discussed, the free gap in axle-box has no effect on wheelset moving directions, but varies the motion amplitudes. For example, the lateral displacements of middle wheelset in Cases 2 and 3 increase by 2.5 and 1.12 mm with respect to the results without free gap. It is an exception occurring in Case 1 that, the corresponding lateral displacement reduces by 1.28 mm. Therefore, the free gap should be considered completely so that the actual motion state can be reflected as accurately as possible.

Figure 10 Influence of free lateral gap on wheelset lateral displacements in asymmetric braking cases

5 Influence of asymmetric braking force on wheelset motions

In the braking operation, the brake shoe forces can produce the corresponding braking forces acting on the wheels directly. For a single brake shoe, the force can be expressed as

                    (21)

The meanings and values of the variables in Eq. (21) can be found in Table 3. The actual brake shoe force calculated is 51.92 kN.

The friction coefficient of high friction composite brake shoe used in the locomotive is a function of brake shoe force and running speed, which is expressed as [22]:

Table 3 Parameters for brake shoe force calculation

          (22)

Combining Eqs. (21) and (22), the braking torque can be calculated in Eq. (23). Clearly, if the asymmetric brake shoe forces occur, the braking torque in left and right side will be different.

                  (23)

As the locomotive brakes at the initial speed of 100 km/h, the friction coefficient and braking torque in a wheel are 0.188 and 6.1 kN·m according to Eqs. (22) and (23). Taking Case 1 as an example and considering the factors mentioned above simultaneously, the wheelset running behaviors under both the braking torque and asymmetric brake shoe forces are investigated. Figure 11 compares the results with and without braking moment in Case 1. The asymmetric brake shoe forces induced by the brake element failure plays a leading role in the bogie special misaligning motion. Whether or not the braking torque is applied for a certain wheelset, the axle has the similar lateral and yawing dynamic responses. The difference of lateral displacement is only below 0.3 mm, while the yaw angle difference is limited to 0.03×10^-6 rad.

6 Influence of BSAT on wheel-rail dynamic interaction in straight line

To research the effect of BSAT on the performance of finished locomotive, Cases 1-6 are discussed, representing the failure of right braking element in the wheelsets 1-6, respectively. Case 0 means no failure occurs, which is regarded as the standard condition. Admittedly, the track random irregularity is the main excitation inducing the vehicle vibration. However, in the braking dynamics simulation, it mainly affects the wheel-rail motion amplitudes without changing the basic movement rules and motion features [12]. In order to highlight the affecting law and action mechanism of asymmetric brake shoe forces, the track irregularity is ignored. For each wheelset in all cases, Figure 12 compares the maximum wheel-rail lateral force, longitudinal force, wheel- rail friction power and wheel-rail contact stress, which are selected as the assessment indices.

Figure 11 Influence of braking torque on wheelset lateral displacement and yaw angles:

The absolute maximum of wheel-rail lateral force and longitudinal force are shown in Figures 12(a) and (b), where WSi and Cj represent the maximum value appears in the ith wheelset and corresponding Case j, respectively. The larger lateral force occurs in Cases 1 and 4, which can reach 5.4 kN increasing by about 4.2 kN with respect to that in Case 0. However, the lateral force for the middle wheelset varies slightly only with an increment below 0.4 kN. The BSAT has a significant influence on the longitudinal creep forces of front (1, 4) and middle (2, 5) wheelset in a bogie, especially that of the middle one. Comparing with the results in Case 0, the longitudinal forces reach 18.1-23.7 kN with an increase of 9.3-13.9 kN when the asymmetric brake shoe forces are applied.

Figure 12 Comparisons of wheel-rail forces for locomotive in different asymmetric braking condition:

Once the BSAT is applied, the wheel-rail friction power values of front (1, 4) and middle (2, 5) wheelsets become larger as shown in Figure 13(a). Even though the asymmetric moments are applied in the rear (4, 6) wheelset, the friction power in middle axle could still increase to 0.9 kW. Generally, if the brake element in one side fails to be close to the front or middle axle, the corresponding wheels may present the violent wear. For example, the maximum friction power of 9.8 kW can be observed in Case 2, which produces an increment of 0.7 kW relative to the 0.28 kW in normal condition. From the aspect of contact strength as shown in Figure 13(b), the wheel-rail contact stress of end wheelsets (1, 3, 4 and 6) is larger than that of the middle wheelset (2, 5). The maximum stress induced by the BSAT can reach 1400-1510 MPa, which exceeds that in Case 0 by 140-250 MPa. The end wheelsets (1, 6) have the worst stress states.

Figure 13 Comparisons of wheel-rail indices for locomotive in different asymmetric braking conditions:

7 Influence of BSAT on wheel-rail dynamic interaction on curved track

The impact of BSAT on the locomotive curving performance is another issue needing to be investigated deeply. According to Ref. [23], the curve minimum radius for newly-built heavy-haul railway lines with speed below 120 km/h is limited to 1200 m in the normal circumstances. For example, the Watang-Rizhao and Haolebaoji-Ji’an heavy-haul railways completed in 2014 and 2019 in sequence have the minimum curve radius of 1200 m. The curve condition represents the typical curve conditions in heavy-haul railways. On account of this, the curve line can be designed as a right curve composed by the circular curve with 1200 m radius, transition curve of 70 m, superelevation of 0.06 m. The locomotive braking initial speed is 100 km/h. As known, the track geometries in curve will lead to the different contact states of inner and outer wheel-rail, which means the failure of left and right brake elements may have asymmetric influence on the locomotive curving performance. Therefore, Cases 1-6 and 1'-6' are considered listed in Table 4. The brake shoe force conditions and typical motion attitudes of wheelsets in curve are displayed in Figure 14. The front and rear bogies of the locomotive are symmetrically equipped, but the axles behave different lateral and yawing displacements relative to the curved track. Clearly, the attack angle of wheelset can be changed oppositely as the left or right brake element fails.

Table 4 Braking element failure cases in curve

Figure 15 compares the dynamic responses of attack angle and wheel-rail lateral forces of 1st wheelset in Cases 0, 1 and 1'. If the braking failure occurs in the outer wheel (Case 1) and inner wheel (Case 1') in sequence, the wheelset attack angle can respectively increase and reduce by about 0.8×10^-3 rad with respect to that in the normal braking condition (Case 0). Correspondingly, the wheel-rail lateral force in Case 1 and Case 1' respectively have the increase and decrease by 8 kN relative to that in Case 0. Therefore, the braking failure in outer wheel deteriorates the wheel-rail lateral dynamic interaction, while the failure in inner side can help the wheelset to yaw towards the radial position and improve the wheel-rail interacting state.

From the perspective of statistics, the maximum values of different wheel-rail dynamic indices in discussed cases are summarized and compared below, so as to find out the most worst operating condition. The attack angle distribution is shown in Figure 16, which indicates that the bogie front wheelset has the larger attack angles no matter the braking forces are applied or not. For outer braking element failure, the maximum attack angles of 2.5×10^-3 and 2.1×10^-3 rad occur in Case 1 and Case 6, corresponding to the wheelsets 1 and 4, respectively. If the inner brake element fails, the peak values of 2.2×10^-3 and 2.3×10^-3 rad can be obtained in Case 3' and Case 4' respectively. Without doubt, the failure in outer or inner braking element has the equivalent influence on wheelset attack angle in the complete locomotive system.

Figure 14 Wheelset motion attitudes in idle running condition and brake shoe force acting states

Figure 15 Dynamic responses of the 1st wheelset in the case of outer and inner brake failure:

Figure 16 Influence of brake failure on wheelset attack angle:

As for the wheel-rail lateral force in Cases 1-6, the values of wheelset 1 in Case 1 and wheelset 4 in Case 6 can respectively reach 25.7 and 20.5 kN with the increments of 8.6 and 3.4 kN comparing with that in Case 0, as shown in Figure 17. For failures in inner brake element of Cases 1'-6', the maximum force is close to 25 kN produced in wheelset 4.

Under the combined influence of wheel-rail longitudinal and lateral forces, the friction power finally peaked in wheelset 1 and 4, as shown in Figure 18. With respect to the results in Case 0, the maximum friction power can increase from 8.3 to 10 and 9.5 kW for the braking failures in Case 1 and Case 1', corresponding to the increments of 1.7 and 1.2 kW in order. There is a certain discreteness in the distribution of wheel-rail normal contact stress, as compared in Figure 19. The braking failure in outer wheel may change the maximum contact stress within the range of 1460-1670 MPa. The worst condition occurs in wheelset 4 of Case 4. When the inner braking element fails, the maximum stress of 1600 MPa occurs in wheelset 2 of Case 3.

Figure 17 Influence of brake failure on wheel-rail lateral forces:

Figure 18 Influence of brake failure on wheel-rail friction power:

Figure 19 Influence of brake failure on wheel-rail contact stress:

Consequently, the contact stress variation induced by the BSAT can reach 210 MPa.

In summary, for the attack angle, wheel-rail lateral force and wheel-rail friction power, the outer braking failure in wheelset 1 can lead to the worst running condition. With regard to the wheel-rail contact stress, the extreme condition corresponds to the outer braking failure in wheelset 4. Once the braking element fails unilaterally, the produced BSAT will deteriorate the locomotive running performance regardless of straight line or curves. Indeed, some field test is important to verify the theoretical results, which will be focused in the following work.

8 Conclusions

By considering the brake shoe forces, the static model of three-axle bogie and dynamic model of locomotive in braking conditions are developed. Then the dynamic behaviors of wheelsets in asymmetric tread brake cases are investigated. The conclusions drawn from the research can be summarized as follows:

1) For a linear mechanical model of three-axle bogie, the same brake shoe asymmetric moment induced by brake failure has different effects on the wheelsets. The front wheelset subjected to the moment can drive all the three wheelsets to move laterally towards the same direction, which even leads to the 4.2 mm offset of wheelset. Otherwise, if it is applied in the middle or rear wheelset, other wheelsets will present opposite motion directions relative to the moment-bearing one. This phenomenon of misaligning motion has not been changed even if the bogie nonlinear properties are included. It is the resultant moment of suspension yawing moment and brake shoe asymmetric moment that determines the wheelset lateral moving amplitude.

2) In asymmetric braking condition, the free lateral gap between wheelset and axle-box can change the wheelset amplitudes of lateral displacements, but not change their motion directions. For the zero free lateral gap, the front and rear wheelsets have the largest lateral displacement respectively, when the brake shoe asymmetric moment is applied in the wheelsets 1-3 in sequence. Conversely, if the free lateral gap is taken into account, the largest lateral displacement occurs in the first and middle wheelsets.

3) With respect to the results in the normal braking on straight line, the increments of wheel-rail lateral force, friction power and contact stress reach 4.2 kN, 0.7 kW and 250 MPa, respectively by the asymmetric brake shoe forces.

4) For asymmetric braking on 1200 m radius curve, the wheel-rail lateral force, friction power and contact stress can maximally increase by 8.6 kN, 1.7 kW and 210 MPa relative to that in normal braking states. The worst condition corresponds to asymmetric braking failure which significantly amplifies the wheelset attack angle, especially for the steering wheelset.

Contributors

LIU Peng-fei provided the investigation method and established the models. ZHANG Kai-long and CAO Yun-qiang carried out the calculation and analyzed the calculation results. The draft of the manuscript was written and edited by LIU Peng-fei, ZHANG Kai-long and CAO Yun-qiang. All authors replied to reviewers’ comments and revised the final version.

Conflict of interest

LIU Peng-fei, ZHANG Kai-long and CAO Yun-qiang declare that they have no conflict of interest.

References

[1] SHA Yong-long. Failure treatment of brake shoe seizure for BFC and BFCF brake unit [J]. Railway Locomotive and Motor Car, 2015(5): 29-31. DOI: 10.3969/j.issn.1003-1820. 2015.05.011. (in Chinese)

[2] ZHANG Ying-yong. Cause analysis and preventive measures for non-brake failure of unit brakes [J]. Railway locomotive & rolling stock workers, 2003(9): 6-9. DOI: 10.3969/ j.issn.1007-6042.2003.09.002. (in Chinese)

[3] WANG Xue-ping, ZHANG Jun, ZHU Huang-shi, SUN Chuan-xi. Analysis of fracture problem of suspended connecting rod in locomotive unit brake [J]. Journal of Beijing University of Civil Engineering and Architecture, 2018, 34(2): 55-59. DOI: 10.3969/j.issn.1004-6011.2018.02. 010. (in Chinese)

[4] BOSSO N, GUGLIOTTA A, MAGELLI M, ORESTA I F, ZAMPIERI N. Study of wheel-rail adhesion during braking maneuvers [J]. Procedia Structural Integrity, 2019, 24: 680-691. DOI: 10.1016/ j.prostr.2020.02.060.

[5] DURALI M, SHADMEHRI B. Nonlinear analysis of train derailment in severe braking [J]. Journal of Dynamic Systems, Measurement, and Control, 2003, 125(1): 48-53. DOI:10.1115/1.1541669.

[6] HANDOKO Y, XIA F J, DHANASEKAR M. Effect of asymmetric brake shoe force application on wagon curving performance [J]. Vehicle System Dynamics, 2004, 41(Suppl.): 113-122.

[7] BELFORTE P, CHELI F, DIANA G, MELZI S. Numerical and experimental approach for the evaluation of severe longitudinal dynamics of heavy freight trains [J]. Vehicle System Dynamics, 2008, 46(Suppl.): 937-955. DOI: 10.1080/00423110802037180.

[8] PUGI L, RINDI A, ERCOLE A G, PALAZZOLO A, AUCIELLO J, FIORAVANTI D, IGNESTI M. Preliminary studies concerning the application of different braking arrangements on Italian freight trains [J]. Vehicle System Dynamics, 2011, 49(8): 1339-1365. DOI: 10.1080/00423114. 2010.505291.

[9] WILSON N, FRIES R, WITTE M, HAIGERMOSER A, WRANG M, EVANS J，ORLOVA A. Assessment of safety against derailment using simulations and vehicle acceptance tests: A world wide comparison of state-of-the-art assessment methods [J]. Vehicle System Dynamics, 2011, 49: 1113-1157. DOI: 10.1080/00423114.2011.586706.

[10] ZHANG Z Y, DHANASEKAR M. Dynamics of railway wagons subjected to braking torques on defective tracks [J]. Vehicle System Dynamics, 2012, 50(1): 109-131. DOI: 10.1080/00423114.2011.571265.

[11] FENG Zhong-li. Study on transmission law of the foundation brake device of C64k cargo train [D]. Beijing: Beijing Jiaotong University, 2016. (in Chinese)

[12] LIU Peng-fei, ZHAI Wan-ming, WANG Kai-yun. Establishment and verification of three dimensional dynamic model for heavy-haul train-track coupled system [J]. Vehicle System Dynamics, 2016, 54(11): 1511-1537. DOI: 10.1080/ 00423114.2016.1213862.

[13] LIU Peng-fei, WANG Kai-yun. Effect of braking operation on wheel–rail dynamic interaction of wagons in sharp curve [J]. Proc IMechE Part K: J Multi-body Dynamics, 2017, 231(1): 252-265. DOI: 10.1177/1464419316662182.

[14] LIU Peng-fei, WANG Kai-yun. Dynamic performance of heavy-haul combined train applying emergency braking on straight line [J]. Journal of Central South University, 2017, 24(8): 1898-1908. DOI: 10.1007/s11771-017-3597-3.

[15] WU Q, COLE C, SPIRYAGIN M, WANG Y C, MA W H, WEI C F. Railway air brake model and parallel computing scheme [J]. Journal of Computational and Nonlinear Dynamics, 2017, 12(5): 051017. DOI: 10.1115/1.4036421.

[16] SHRESTHA S, SPIRYAGIN M, WU Q. Friction condition characterization for rail vehicle advanced braking system [J]. Mechanical Systems and Signal Processing, 2019, 134: 106324. DOI: 10.1016/j.ymssp.2019.106324.

[17] GUNAY M, KORKMAZ M, OZMEN R. An investigation on braking systems used in railway vehicles [J]. Engineering Science and Technology, an International Journal, 2020, 23(2): 421-431. DOI: 10.1016/j.jestch.2020.01.009.

[18] MAZZU A, PROVEZZA L, ZANI N, PETROGALLI C, GHIDINI A, FACCOLI M. Effect of shoe braking on wear and fatigue damage of various railway wheel steels for high speed applications [J]. Wear, 2019, 434-435: 203005. DOI: 10.1016/j.wear.2019.203005.

[19] XIE Jian-ping, CHEN Zhi-ya, YANG Kun, WANG Jue. Analysis and improvement measures of JDYZ-5 compact unit brake shoe [J]. Journal of Railway Science and Engineering, 2019, 16(9): 2312-2316. DOI: 10.19713/j.cnki. 43-1423/u.2019.09.024. (in Chinese)

[20] LIU Peng-fei, WANG Kai-yun, ZHANG Kai-long, CAO Yun-qiang. Asymmetric motions of bogie front and rear wheelset under unbalanced brake shoe pressures [J]. China Railway Science, 2019, 40(5): 95-102. DOI: 10.3969/j.issn. 1001-4632.2019.05.13. (in Chinese)

[21] ZHAI Wan-ming. Vehicle-track coupled dynamics [M]. Beijing: Science Press, 2015. (in Chinese)

[22] TB/T1407.1-2018. Railway train traction calculation-Part 1: Trains with locomotives [S]. Beijing: National Railway Administration of China, 2018. (in Chinese)

[23] TB10098-2017. Code for design of railway line [S]. Beijing: National Railway Administration of China, 2017. (in Chinese)

(Edited by FANG Jing-hua)

中文导读

不对称闸瓦力作用下六轴机车动态特性

摘要：本文研究了轮对左、右侧闸瓦压力及制动力不对称状态下机车的动力学行为。首先建立了三轴转向架静力学平衡模型和机车动力学模型，并推导了悬轴电机与轮对的耦合振动方程；进而研究了不对称闸瓦作用力对轮对非对称运动和轮轨力学特性的影响。结果表明，如果在前轮对上作用不对称闸瓦力，所有轮对都沿同一方向横向运动，一旦该作用力出现在中间或后部轮对，则其余轮对会向相反的方向横移，在不对称制动条件下，轮对自由横动量可以增大轮对运动幅度，但不会改变运动方向。最后，分析了直线和曲线上闸瓦不对称制动时机车的运行状态，结果显示，不对称闸瓦力可诱发轮对的错位运动，加剧轮轨横向动态相互作用、恶化轮轨接触状态，特别是导向轮对，不对称制动会急剧增大轮对冲角，是为最不利的制动工况。

关键词：机车；闸瓦压力；动力学特性；不对称制动；轮轨接触

Foundation item: Projects(52072249, 51605315) supported by the National Natural Science Foundation of China; Project(E2018210052) supported by the Natural Science Foundation of Hebei Province, China; Project(TPL1707) supported by the Open Funds for the State Key Laboratory of Traction Power, China

Received date: 2020-02-22; Accepted date: 2020-06-14

Corresponding author: LIU Peng-fei, PhD, Associate Professor; Tel: +86-311-87935238; E-mail: lpfswjtu@163.com; ORCID: https:// orcid.org/0000-0002-4017-1205