J. Cent. South Univ. (2019) 26: 1794-1806

DOI: https://doi.org/10.1007/s11771-019-4134-3

Limit variation analysis of shallow rectangular tunnels collapsing with double-layer rock mass based on a three-dimensional failure mechanism

ZHAO Lian-heng(赵炼恒)^{1, 2}, HU Shi-hong(胡世红)¹, YANG Xin-ping(杨新平)¹,HUANG Fu(黄阜)³, ZUO Shi(左仕)¹

1. School of Civil Engineering, Central South University, Changsha 410075, China;

2. Key Laboratory of Heavy-Haul Railway Engineering Structure (Ministry of Education), Central South University, Changsha 410075, China;

3. School of Civil Engineering and Architecture, Changsha University of Science and Technology,Changsha 410004, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: In the framework of upper bound theorem of limit analysis, the progressive collapse of shallow rectangular tunnels with double-layer rock mass has been theoretically analyzed based on the three-dimensional (3D) velocity discontinuity surfaces. According to the virtual work principle, the difference theorem and the variation method, the collapse surface of double-layer rock mass is determined based on the Hoek-Brown failure criterion. The formula can be degenerated to a single-layer rock collapsing problem when the rock mass is homogeneous. To estimate the validity of the result, the numerical simulation software PLAXIS 3D is used to simulate the collapse of shallow tunnels with double-layer rock mass, and the comparative analysis shows that numerical results are in good agreement with upper-bound solutions. According to the results of parametric analysis, the potential range of collapse of a double-layer rock mass above a shallow cavity decreases with a decrease in A₁/A₂, σ_ci1/σ_ci2 and σ_tm1/σ_tm2 and an increase in B₁/B₂, γ₁/γ₂. The range will decrease with a decrease in support pressure q and increase with a decrease in surface overload σ_s. Therefore, reinforced supporting is beneficial to improve the stability of the cavity during actual construction.

Key words: shallow tunnels; three-dimensional collapse; double-layer rock mass; Hoek-Brown failure criterion; variation analysis; upper bound limit analysis

Cite this article as: ZHAO Lian-heng, HU Shi-hong, YANG Xin-ping, HUANG Fu, ZUO Shi. Limit variation analysis of shallow rectangular tunnels collapsing with double-layer rock mass based on a three-dimensional failure mechanism [J]. Journal of Central South University, 2019, 26(7): 1794-1806. DOI: https://doi.org/10.1007/s11771-019-4134-3.

1 Introduction

With the accelerated process of urbanization in the world (such as China), a large number of people have gathered in the city, resulting in increasing urban population density. The land for construction is becoming increasingly crowded. To solve this problem, the development and utilization of underground space have been highly valued by the planning departments at all levels, and more and more shallow underground buildings are appearing in urban construction. Because there are thin rock and soil layers covering the shallow underground structures, there is likely to be ground collapse caused by poor support measures during the excavation process. Therefore, the stability of shallow cavities has attracted the attention of researchers in related fields.

To solve this problem, FRALDI et al [1-4] firstly deduced the expression of the two- dimensional collapse shape of a rectangular cavity or arbitrary cross section based on the nonlinear Hoek-Brown failure criterion and performed theoretical research on progressive failure of tunnel collapse. HUANG et al [5] constructed the failure mechanism of circular deep buried tunnel with the Hoek-Brown failure criterion considering the effects of pore water pressure. YANG et al [6] proposed the mechanism of two-dimensional circular shallow tunnel considering the support effect based on the upper bound theorem of limit analysis and variation method, and deduced the expression of collapse and drew the surface collapsing shapes under different parameters. YANG et al [7] considered effects of seepage forces and discussed the potential collapse shape of deep tunnels in layered soils. Further, based on the Power-Law failure criterion and non-associated flow rule, the failure mechanism of tunnel roof in homogeneous and layered soils were studied by YANG et al [8]. QIN et al [9] constructed the collapse mechanism of deep buried tunnels based on the Hoek-Brown yield criterion under the circumstance that strength parameters were weakened because of weathering of the rock formation and some other reasons and deduced the surface collapse shape, which was the same as the results of FRALDI et al [1-4].

In practical engineering, the failure process of the rock mass is a three-dimensional evolution process. The above plane-strain model can only reflect two-dimensional morphological characters of surrounding rock on the surface of shallow cavity stability but cannot perform true three- dimensional failure analysis. For given that, YANG et al [10] derived the three-dimensional collapse mechanism of deep buried rectangular tunnels based on the Hoek-Brown failure criterion, and LUO at al [11] considered the effect of supporting pressure. QIN et al [12] established the surrounding rock failure mechanism above the shallow cavity affected by seepage pressure according to the upper bound theorem of limit analysis. XIA et al [13] investigated the safety factor of shallow buried tunnels through the strength reduction method (SRM) under different depths. LIU et al [14] studied the failure process with a number of three-dimensional model tests, and the failure mode of shallow tunnels at different thickness-span ratios was obtained. By proposing a symmetric 3D rotational progressive failure mechanism that considered the presence of rock layers partly induced by weathering through an analytical upper-bound approach, QIN et al [15] determined the range and shape of potential falling blocks using the variational principle and the partition optimization method.

The above research on the stability of a shallow cavity considered homogeneous single rock stratum. However, the layering of a rock mass is extremely common in practice, and underground structures are always constructed in a stratified rock mass. QIN et al [16] established 2D and 3D collapse mechanisms for deep tunnels under the condition of varying water table, and the upper bound solutions of collapsing blocks were obtained. Further, QIN et al [17] considered the heterogeneity of rock properties, and the effective collapse mechanism was derived by using the discretized approach.

Most of existing researches are based on a stress boundary condition that the shear stress is equal to 0 at point x=0 (FRALDI et al [1-4]), but this point does not exist in shallow tunnels, this will lead to the collapse range increase with an increase in surface overload, which may not be conformed with the real case. The main purpose of this paper is to study the stability of shallow cavities with multilayer and different rock mass properties, and extend the research on deep tunnels by YANG et al [10] and QIN et al [12, 15, 16] to stratified shallow tunnels. A three-dimensional failure mechanism of surrounding rocks above a shallow cavity was established by considering the stratification of the surrounding rock, according to the upper bound limit analysis. The objective function which includes the first derivative expression of three-dimensional failure surface of the double-layer rock mass was obtained. The upper bound solution of the first derivation equation for double-layer collapsing blocks was optimized by the variation approach, then the 3-D shape of collapsing was obtained with the help of difference theorem and boundary conditions. Most important of all, we lead into the effect of the surface overload σ_s on the collapsing failure mechanism by using the stress boundary condition, which cannot be seen in the existing research. Also, the numerical simulation software PLAXIS 3D was used to simulate the collapse of shallow tunnels with double-layer rock mass, and the comparative analysis shows that numerical results are in good agreement with upper-bound solutions, which can illustrate the validity of this method. We hope that this paper could provide a theoretical basis for the prediction of the potential collapse range of surrounding rocks above the shallow cavity in stratified rock.

2 Upper bound theorem of limit analysis

The upper bound theorem of limit analysis can be expressed as a kinematically admissible velocity assumed to satisfy the boundary condition, the velocity strain and velocity field compatibility condition, load T_i and X_i determined by the virtual power equation are no less than the real limit load.

               (1)

where and 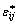represent the stress and strain rate in the kinematically admissible velocity field; T_i is a surface load acting on research objects; X_i is the body force acting on research objects; V_i is the velocity vector in the kinematically admissible velocity field; s is the load boundary; and v is the volume of the collapsing blocks.

3 Hoek-Brown failure criterion and associated flow rule

According to the upper bound theorem of limit analysis, the collapsing failure mechanism of double layer rock mass in shallow tunnels includes velocity discontinuity of the fracture surface, which also can be called a velocity discontinuity surface. The results of FRALDI et al [1-4] showed that the energy dissipation of any point on the velocity discontinuity surface can be obtained by the shear and normal stress. Therefore, the Hoek-Brown failure criterion, expressed by the normal and shear stress as follows [18], was used to calculate the energy dissipation along the velocity discontinuity surface:

                       (2)

where A and B represent dimensionless constants characterizing the properties of rock mass, τ is the shear stress, σ_n is the normal stress, σ_ci is the uniaxial compressive strength and σ_tm is the tensile strength of the rock mass.

It is assumed that the rock mass obeys the Hoek-Brown failure criterion and an associated flow rule, the plastic potential surface coincides with the failure surface, and the plastic potential function can be expressed by the Hoek-Brown failure function as follows:

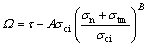                   (3)

According to the associated flow rule, the plastic strain increment is proportional to the stress gradient of the plastic potential function.

            (4)

where λ is a scalar parameter.

4 Upper bound analysis of three- dimensional collapse of a double- layer rock mass above a shallow cavity

4.1 Three-dimensional failure mechanism of a double-layer rock mass

The three-dimensional failure mechanism of the double-layer of surrounding rock at the top of a shallow cavity is shown in Figure 1. The velocity discontinuities are made up of two curved lines, namely f₁(x) and f₂(x). L₁, L₂ and L₃ are the half failure widths at the ground surface, the interface of rock strata and the top of the cavity. The thickness of the upper and lower layer rock mass is H₁ and H₂, and the bulk density of the geo-material is γ₁ and γ₂. And two external forces, σ_s and q, are acting on the ground surface and the top of the cavity respectively.

4.2 Collapsing energy calculation based on 3-D failure mechanism

Suppose that the equation of velocity discontinuity surface is f(x), and the slope of the tangent at any point along the velocity discontinuity surface can be expressed by the first derivative f'(x) of the curve equation, and the normal and shear velocities at any point on the velocity discontinuity surface also can be determined by f'(x). Using trigonometric transformation, and then the normal and shear plastic strain rate can be obtained as follows:

                 (5)

where t represents the thickness of the velocity discontinuity surface, and v is the velocity of the rigid collapse block.

Figure 1 Three-dimensional failure mechanism of double-layer rock mass above shallow cavity:

According to the researches of FRALDI et al [1-4], the energy dissipation at any point on the velocity discontinuity surface can be obtained by the normal and shear stress.

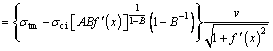 (6)

The lateral area of the collapse failure mechanism can be obtained by the formula of the side area of the rotational body.

                    (7)

According to Eqs. (6) and (7), the work rate of the internal energy dissipation generated on the whole 3-D discontinuity surface can be calculated.

            (8)

The work rate of gravitation of the collapse block of the double layers can be expressed as follows:

                  (9)

The work rate of support pressure q is

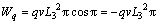                (10)

The surface overload has great influence on the shape of the failure surface because of the failure surface of the shallow buried tunnel extending to the ground surface, which is different from the deep buried tunnel. Therefore, it is necessary to consider the work rate of the surface overload during the research on the failure surface of the shallow buried tunnel. The work rate of the surface overload can be derived based on the area of the collapsing block extending to the ground surface and the surface surcharge σ_s.

                            (11)

According to the virtual work principle, the work rate of the internal energy dissipation is equal to the total work rates of external forces.

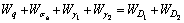             (12)

The objective function containing f₁(x) and f₂(x) was constructed to obtain the upper bound solution of the failure surface:

                       (13)

where the specific expressions of 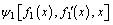and are as follows:

   (14)

As seen from the previous formula (14), the extreme value of ξ is completely determined by 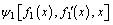and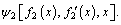Since the independent variable f₁(x) in Ψ₁ and f₂(x) in Ψ₂ are functions, Ψ₁ and Ψ₂ are both functions; this functional extremum problem is converted by a variation calculation to an Euler equation definite solution problem and the boundary condition is satisfied. The Euler equations corresponding to Ψ₁ and Ψ₂ are:

                  (15)

where

 (16)

Substituting formula (16) into formula (15), we can obtain equations as follows:

(17)

Thus

 (18)

where c₁ and c₂ are both integral constants, which can be determined by boundary conditions.

According to the geometric relationship shown in Figure 1, the boundary conditions are as follows.

                     (19)

As the shear stress on the earth surface is 0, the microelement of the surface is taken for analysis, as shown in Figure 2. It could be seen that the horizontal component of the stress τ_xz= 0, which satisfies:

                      (20)

Among them, the shear stress component τ_xz on the separated layer is expressed according to the microelement as follows:

                 (21)

which is not different from the formula in the researches of FRALDI et al [1-4] as follows unless σ does not exist in Figure 2.

                  (22)

where

                      (23)

At the rock interface, there does not exist relative sliding and the deflection compatibility must be satisfied, so the plastic strain rate of upper and lower layers at the intersection is equal [19, 20].

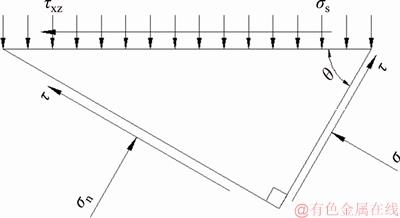
Figure 2 Microelement of surface

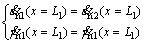                  (24)

Through simplification,

                   (25)

According to the upper bound theorem of limit analysis, the work rate of the internal energy dissipation is equal to total work rates of external forces.

                                  (26)

By Eqs. (19), (20), (24) and (26), we can obtain the numerical solutions of L₁, L₂, L₃, c₁ and c₂ by using difference theorem [21, 22]. Then the shape of failure curve and the three-dimensional shape of the double layers surrounding rocks collapsing at the top of the shallow cavity can be plotted by using the numerical software Matlab.

4.3 Three-dimensional failure mechanism of a single-layer rock

When the parameters of the upper blocks coincide with the lower blocks, the failure mechanism of the double-layer rock mass degenerates into the problem of researching the collapse failure mechanism of a single-layer rock. That is

                       (27)

And then we can simplify formulas (8), (9), (10) and (11) as follows.

The work rate of the internal energy dissipation is:

 (28)

where L₁ and L₃ are damage radius of ground and shallow tunnel roof.

The work rate of gravitation of the collapse block, support pressure and the surface overload are:

               (29)

According to the virtual work principle and Euler equation, the first derivative expression of the three-dimensional collapsing failure surface under single layer rock can be written as follows:

     (30)

where c₁ is integral constants, which can be determined by employing boundary conditions as follows:

                          (31)

where H is the thickness of the rock mass.

The stress boundary condition and the work rate balance condition are the same as mentioned before. By Eqs. (21), (26) and (31), we can obtain the numerical solutions of L₁, L₃, and c₁ and the three-dimensional shape of the single layer surrounding rocks collapsing at the top of the shallow cavity by using difference theorem. Therefore, when parameters of the double-layer rock masses are coincident, the research object of this paper degenerates into a single-layer rock collapse problem.

5 Numerical calculation and analysis

5.1 Comparative analysis of rock collapse with two different methods

When B=0.5, the analytic solutions of L₁ and L₃ could be obtained. Adopt two different methods to calculate the radius L₁ and L₃ of the top and the bottom of the three-dimensional collapsing blocks above the shallow cavity. The first method obtained the analytic solution of the three-dimensional collapse failure curve equation by integration directly, and the second obtained the numerical solution by using difference theorem [21, 22]. Comparison of the two methods proves the effectiveness of difference method in this paper.

When parameters of rock mass are A₁=A₂=0.3, B₁=B₂=0.5, σ_ci1=σ_ci2=2.5 MPa, γ₁=γ₂=20 kN/m³, q= 10 kPa, H₁=H₂=3 m, the influence curves of the numerical solution, L₁ and L₃, of this paper when σ_s=0-50 kPa under the conditions of σ_tm1 is equal to σ_tm2 or not, were obtained, as shown in Figure 3.

As seen from Figure 3, when the surrounding rock parameters are consistent, the numerical solutions by using difference method of the radius of L₁ and L₃ is the same as the analytic solutions. This can prove the effectiveness of the difference method of this paper on the three-dimensional collapse failure of double-layer rocks above a shallow cavity.

Figure 3 Comparison of top and bottom radius with two methods:

5.2 Influence of different geo-material parameters on 3-D failure mechanism of collapsing block above a shallow cavity

According to Eq. (13), the form of the parameter combination of double-layer surrounding rocks is complex. To simplify the analysis, the influence on the 3-D failure mechanism of the collapsing blocks above a shallow cavity with the change of parameter ratios was analyzed. The influence with the change of ratios of A₁/A₂, B₁/B₂, γ₁/γ₂, σ_ci1/σ_ci2, σ_tm1/σ_tm2 and q, σ_s on the collapse shape was analyzed when H₁=H₂=3 m, and the shapes are drawn in Figures 4 and 5.

From Figures 4 and 5, the collapse block of the double-layer surrounding rock is a rotating block of curves f₁(x) and f₂(x) rotating around the z-axis. According to the shape of the collapse surface with different parameters, we can draw the conclusion, no matter how parameters change, that the shape of the collapse surface of the tunnel is a parabola, and the shape of each layer is similar to a spatial “inverted funnel”.

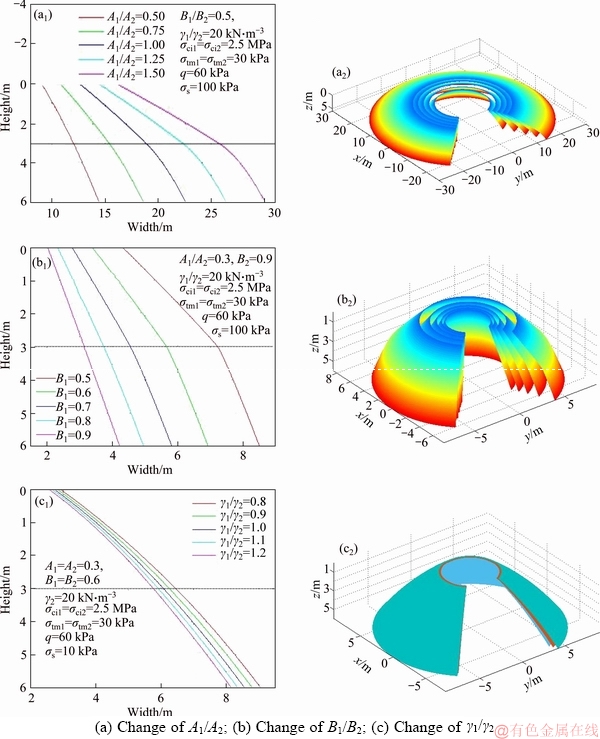
Figure 4 Shape of collapse surface with different parameters:

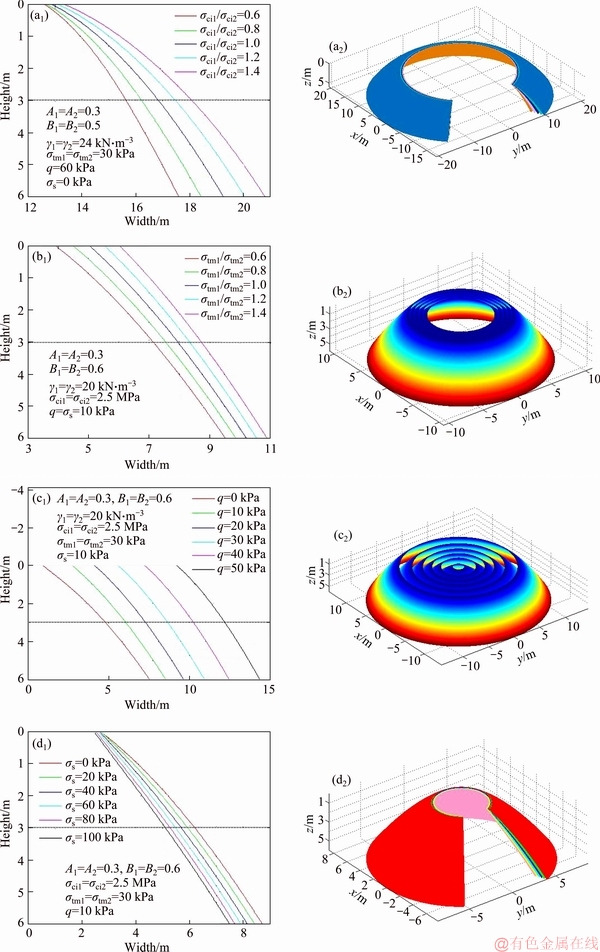
Figure 5 Shape of collapse surface with change of σ_ci1/σ_ci2 (a), σ_tm1/σ_tm2 (b), q (c) and σ_s (d)

Ratios of A₁/A₂ and B₁/B₂ have great influence on the shape of the collapse surface of tunnels. The collapse range of the tunnel increases with an A₁/A₂ increase. When A₂ is fixed, with an increase in A₁, the collapse range of the upper and lower rocks will increase. The influence of B₁/B₂ is different from A₁/A₂, L₁ and L₂, and the collapse range L₃ of the tunnel all decreases with a B₁/B₂ increase. When B₂ is fixed, with an increase in B₁, the collapse range of the upper and lower rocks will decrease. The upper and lower rocks collapse range will increase with σ_ci1/σ_ci2, σ_tm1/σ_tm2 increasing, but decrease with γ₁/γ₂ increasing. The surface overload σ_s has great influence on the shape of the failure surface because the failure surface of a shallow tunnel would extend to the ground surface. The upper and lower rocks tend to collapse within a smaller range with an increase in σ_s. If the collapse range L₃ is determined, the surrounding rock is more stable with an increase in the surface load σ_s. The upper and lower rocks tend to collapse in a larger range with an increase in q. If the effective width of the support pressure q is determined, the surrounding rock is more stable with an increase in the support pressure q. Therefore, for the double-layer rocks of a shallow tunnel, when geotechnical parameters ratios of A₁/A₂, σ_ci1/σ_ci2 and σ_tm1/σ_tm2 are smaller and ratios of B₁/B₂ and γ₁/γ₂ are larger, the range of potential collapse surface is smaller, and it is safer for tunnel construction.

5.3 Numerical analysis

The PLAXIS 3D program is a powerful general geotechnical finite element calculation software that is an FE package specially developed for the deformation and stability analysis in geotechnical engineering problems [23]. It can well simulate the interaction between soil layers. Therefore, to evaluate the validity of the method presented herein, the numerical simulation software PLAXIS 3D is used to simulate the collapse of shallow tunnels with double-layer rock mass. Based on the upper-bound limit analysis theory, the rate of internal energy dissipation on the velocity discontinuity surface is calculated by normal stress and shear stress strains, and the H–B failure criterion expressed in terms of normal and shear stresses is employed, i.e., Eq. (2). However, the H–B failure criterion can also be represented by major and minor principal stresses [24, 25] as follows:

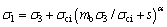               (32)

where σ₁ and σ₃ are the major and minor effective principal stresses, respectively; σ_ci, m_b, s and α are material parameters that can be associated with the geological strength index (GSI).

The parameters of the H–B criterion expressed in the two forms are evidently different. To compare the upper-bound calculations with the numerical results under the same conditions, it is necessary to maintain the parameters, i.e., the parameters in one form need to be transformed to the parameters in another equivalent form [24, 25]. Fortunately, HOEK et al [18] proposed a method to achieve this parameter transformation. Based on a linear regression analysis, parameters A and B can be determined when σ_ci, m_b, and the GSI are given. Further, three sets of equivalent parameters exist for the two forms of H–B failure criterion, as listed in Table 1.

Table 1 Equivalent parameters for the two forms of H-B failure criterion

Considering the symmetry of the collapse failure mechanism constructed in this study (Figure 1), we use 1/4 of the failure mechanism for analysis. The size of the model is 20 m (x)×20 m (y)×15 m (z), without considering the influence of water level; the thicknesses of the double-layer rock mass are both 2.5 m, the width of the rectangular tunnel is 3.2 m, the parameters of the upper rock mass are value I, and those of the lower rock mass are value II. Because the bulk density has little influence on the collapse range of the tunnel, the rock mass bulk density is 20 kN/m³, and the plastic calculation is performed. The total displacement distribution in PLAXIS 3D representing the collapse range of the shallow tunnel is shown in Figure 6.

To better compare the failure surface obtained from the upper-bound theorem and that from the numerical simulation, the failure surface obtained from Eqs. (19), (20), (24) and (26) is superimposed on Figure 6 with the equivalent parameters listed in Table 1. Further, when the parameters of the upper and lower rock masses are identical, it degenerates into the collapse of homogeneous rock mass in a shallow tunnel. The rock mass parameters are value III, the width of the rectangular tunnel is 1.9 m, and the rock mass weight is still 20 kN/m³. The collapse of a single rock mass overlying the shallow tunnel is analyzed, and the numerical results are shown in Figure 7.

The red line in Figures 6 and 7(a) represents the failure surface calculated by the upper-bound method. As shown in Figures 6 and 7, the difference in the double-layer rock mass collapse range between the upper-bound calculation and the numerical result is significant, but the difference in the single-layer rock mass is small. This is due to the error of the H–B criterion rock mass parameters in transformation, and a gap will exist between the upper-bound calculation and the numerical result. However, in general, the upper-bound solution of the collapse surface obtained by the upper-bound theory of limit analysis and the numerical analysis result are the same and both are acceptable in the range of permissible error.

6 Conclusions

1) Based on the upper bound theorem of limit analysis and Hoek-Brown failure criteria, a 3-D failure mechanism of the shallow tunnel was constructed. According to energy consumption calculations and the variation method, the first derivative expression of the shape of the tunnel collapse surface was obtained. The collapse range of the shallow cavity was calculated by using Matlab software according to difference theorem,and a three-dimensional image of the collapse block was drawn. A theoretical basis for the potential collapse range of the double-layer rock mass above the shallow cavity for practical engineering was provided.

Figure 6 Comparison of failure surface provided by upper-bound theorem and numerical simulation (double-layer rock mass):

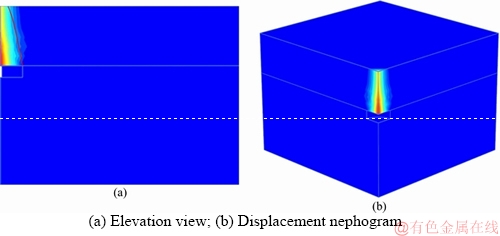
Figure 7 Comparison of failure surface provided by upper-bound theorem and numerical simulation (single-layer rock mass):

2) Ratios of the geo-material parameters A₁/A₂, B₁/B₂, γ₁/γ₂, σ_ci1/σ_ci2 and σ_tm1/σ_tm2 have great effect on the collapse surface shape of the shallow tunnel and the collapse range. The collapse range of the upper and lower rocks will increase with an increase in A₁/A₂, σ_ci1/σ_ci2 and σ_tm1/σ_tm2 but decrease with an increase in B₁/B₂ and γ₁/γ₂. Therefore, the smaller ratios of A₁/A₂, σ_ci1/σ_ci2 and σ_tm1/σ_tm2 and the larger ratios of B₁/B₂ and γ₁/γ₂ will decrease the potential collapse range of the double-layer rock mass above the shallow cavity. It is beneficial to improve the stability of the shallow cavity during actual construction.

3) When the surface load σ_s is larger and the support pressure q is smaller, the double-layer rocks above a shallow tunnel tend to collapse with a smaller range. In addition, when the collapse range L₃ is determined, it is more advantageous for the stability of surrounding rocks of a shallow cavity when the surface load σ_s and the support pressure q are larger. Therefore, a stronger support structure to reduce the risk of collapse of the double-layer rock mass above a shallow cavity should be used when the underground cavity is constructed in the center of the city, which has more buildings and a larger surface load.

References

[1] FRALDI M, GUARRACINO F. Limit analysis of collapse mechanisms in cavities and tunnels according to the Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(4): 665-673. DOI: 10.1016/j.ijrmms.2008.09.014.

[2] FRALDI M, GUARRACINO F. Analytical solutions for collapse mechanisms in tunnels with arbitrary cross sections [J]. International Journal of Solids and Structures, 2010, 47(2): 216-223. DOI:10.1016/j.ijsolstr.2009.09.028.

[3] FRALDI M, GUARRACINO F. Evaluation of impending collapse in circular tunnels by analytical and numerical approaches [J]. Tunnelling and Underground Space Technology, 2011, 26(4): 507-516. DOI: 10.1016/j.tust.2011. 03.003.

[4] FRALDI M, GUARRACINO F. Limit analysis of progressive tunnel failure of tunnels in Hoek–Brown rock masses [J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 50: 170-173. DOI: 10.1016/ j.ijrmms.2011.12.009.

[5] HUANG F, YANG X L. Upper bound limit analysis of collapse shape for circular tunnel subjected to pore pressure based on the Hoek-Brown failure criterion [J]. Tunnelling and Underground Space Technology, 2011, 26: 614-618. DOI: 10.1016/j.tust.2011.04.002.

[6] YANG X L, HUANG F. Collapse mechanism of shallow tunnel based on nonlinear Hoek–Brown failure criterion [J]. Tunnelling and Underground Space Technology, 2011, 26(6): 686-691. DOI:10.1016/j.tust.2011.05.008.

[7] YANG X L, YAN R M. Collapse mechanism for deep tunnel subjected to seepage force in layered soils [J]. Geomechanics and Engineering, 2015, 8(5): 741-756. DOI: 10.12989/gae. 2015.8.5.741.

[8] YANG X L, XU J S, LI Y X. Collapse mechanism of tunnel roof considering joined influences of nonlinearity and non-associated flow rule [J]. Geomechanics and Engineering, 2016, 10(1): 21-35. DOI: 10.12989/gae.2016.10.1.021.

[9] QIN C B, YANG X L, PAN Q J, SUN Z B, WANG L L, MIAO T. Upper bound analysis of progressive failure mechanism of tunnel roofs in partly weathered stratified Hoek-Brown rock masses [J]. International Journal of Rock Mechanics and Mining Sciences, 2015, 74: 157-162. DOI: 10.1016/j.ijrmms.2014.10.002.

[10] YANG X L, HUANG F. Three-dimensional failure mechanism of a rectangular cavity in a Hoek–Brown rock medium [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 61: 189-195. DOI: 10.1016/ j.ijrmms.2013.02.014.

[11] LUO W H, LI W T. Reliability analysis of supporting pressure in tunnels based on three-dimensional failure mechanism [J]. Journal of Central South University, 2016, 23(5): 1243-1252. DOI: 10.1007/s11771-016-0374-7.

[12] QIN C B, SUN Z B, LIANG Q. Limit analysis of roof collapse in tunnels under seepage forces condition with three-dimensional failure mechanism [J]. Journal of Central South University, 2013, 20(8): 2314-2322. DOI: 10.1007/ s11771-013-1739-9.

[13] XIA C C, ZHAO X, ZHANG G Z, WANG C B. Stability analysis by strength reduction method in shallow buried tunnels [J]. Tunneling and Underground Construction, 2014, 242: 321-331. DOI: 10.1061/9780784413449.032.

[14] LIU J, LIU X R, LAI Y, HE C M, WANG Z J. Failure mode of shallow-buried weak tunnel under different thickness-span ratios [J]. Journal of Central South University: Science and Technology, 2016, 47(5): 1744-1751. DOI: 10.11817/j.issn. 1672-7207.2016.05.038. (in Chinese)

[15] QIN C B, CHIAN S C, YANG X L. 3D limit analysis of progressive collapse in partly weathered hoek–brown rock banks [J]. International Journal of Geomechanics, 2017, 17(7), 04017011(1–10). DOI: 10.1061/(asce)gm.1943-5622. 0000885.

[16] QIN C B, CHIAN S C, YANG X L, DU D C. 2D and 3D limit analysis of progressive collapse mechanism for deep-buried tunnels under the condition of varying water table [J]. International Journal of Rock Mechanics and Mining Sciences, 2015, 80: 255-264. DOI: 10.1016/ j.ijrmms.2015.09.024.

[17] QIN C B, CHIAN S C. Revisiting crown stability of tunnels deeply buried in non-uniform rock surrounds [J]. Tunnelling and Underground Space Technology, 2018, 73: 154-161. DOI: 10.1016/j.tust.2017.12.006.

[18] HOEK E, BROWN E T. Practical estimate the rock mass strength [J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(8): 1165-1186. DOI: 10.1016/ S0148-9062(97)00305-7.

[19] ZHAO L H, TAN Y G, NIE Z H, YANG X P, HU S H. Variation analysis of ultimate pullout capacity of shallow horizontal strip anchor plate with 2-layer overlying soil based on nonlinear M-C failure criterion [J]. Journal of Central South University, 2018, 25: 2802-2818. DOI: 10.1007/s11771-018-3954-x.

[20] ZHANG R, LU S P. Kinematic analysis of shallow tunnel in layered strata considering joined effects of settlement and seepage [J]. Journal of Central South University, 2018, 25(2): 368-378. DOI: 10.1007/s11771-018-3743-6.

[21] ZHAO L H, YANG X P, HUANG F, TAN Y G, HU S H. Variational analysis of the ultimate pullout capacity of shallow circular anchor plates in rock foundations based on the Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 106: 190-197. DOI: 10.1016/j.ijrmms.2018.04.027.

[22] ZHAO L H, TAN Y G, HU S H, DENG D P, YANG X P. Upper bound analysis of the ultimate pullout capacity of shallow 3-D circular plate anchors based on the nonlinear mohr-coulomb failure criterion [J]. Journal of Central South University, 2018, 25: 2272-2288. DOI: 10.1007/s11771-018- 3912-7.

[23] BRINKGREVE R B J, VERMEER P A. Finite element code for soil and rock analyses [M]. Rotterdam: A.A. Balkema, 1998.

[24] HUANG F, ZHAO L H, LING T H, YANG X L. Rock mass collapse mechanism of concealed Karst cave beneath deep tunnel [J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 91: 133-138. DOI: 10.1016/ j.ijrmms.2016.11.017.

[25] HUANG F, OU R C, LI Z L, YANG X L, LING T H. Limit analysis for the face stability of a shallow-shield tunnel based on a variational approach to the blow-out failure mode [J]. International Journal of Geomechanics, 2018, 18(6): 04018038. DOI: 10.1061/(asce)gm.1943-5622.0001150.

(Edited by HE Yun-bin)

中文导读

基于三维破坏机制的浅埋矩形硐室顶部双层围岩塌落上限变分分析

摘要：根据极限分析上限定理，基于三维速度间断面破坏机制理论分析了浅埋矩形硐室顶部双层围岩的渐进式塌落。根据虚功原理、差分定理和变分法，确定了Hoek-Brown破坏准则条件下双层岩体的塌落面。该公式可退化为岩体性质均匀时的单层岩体塌落问题。为验证计算结果的有效性，采用数值模拟软件PLAXIS 3D分析了浅埋硐室顶部双层围岩的塌落，对比分析表明，数值模拟结果与上限解吻合较好。参数分析表明，浅埋隧道顶部双层岩体的潜在塌落范围随A₁/A₂、σ_ci1/σ_ci2、σ_tm1/σ_tm2的减小而减小，随B₁/B₂、γ₁/γ₂的增大而减小。塌落范围随着支护压力q的减小而减小，随着表面超载σ_s的减小而增大。因此，加强支护有利于提高实际施工中隧道的稳定性。

关键词：浅埋隧道；三维塌落；双层岩体；Hoek-Brown破坏准则；变分分析；上限分析

Foundation item: Projects(51478477, 51878074) supported by the National Natural Science Foundation of China; Project(2017-123-033) supported by the Guizhou Provincial Department of Transportation Foundation, China; Projects(2018zzts663, 2018zzts656) supported by the Fundamental Research Funds for the Central Universities, China

Received date: 2019-03-06; Accepted date: 2019-04-22

Corresponding author: ZUO Shi, PhD; Tel: +86-13687394904; E-mail: zuoshi@csu.edu.cn; ORCID: 0000-0002-7056-3322; HUANG Fu, PhD, Lecturer; Tel: +86-13975146439; E-mail: hfcsu0001@163.com; ORCID: 0000-0002-5868-8659