J. Cent. South Univ. Technol. (2007)01-0120-05

DOI: 10.1007/s11771-007-0024-1               

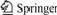
Analysis of steel-concrete composite structure with overlap slab of Xingguang bridge

YE Mei-xin(叶梅新), HUANG Qiong(黄 琼), WU Qin-qin(吴芹芹)

(School of Civil and Architectural Engineering, Central South University, Changsha 410075, China)

Abstract: Finite element modeling methods of steel-concrete composite structure with overlap slab were investigated. A two-step finite element method was presented. It was applied to analyze an extra long span composite bridge. The conversion of structure system and the mechanical behavior of the bridge were analyzed with two different construction methods. The stresses of steel beams, precast slabs and in-situ-place concrete under the total load were compared. The results show that steel-concrete composite structure with overlap slab has many advantages, the construction method that the top in-situ concrete and the concrete in construction joints are cast respectively is rather reasonable than the one that the top in-situ concrete and the concrete in construction joints are cast at the same time, and the two-step finite element method is affective to such large-scale structures.

Key words: composite structure; numerical method; two-step finite element method; mechanical behavior

1 Introduction

Steel-concrete composite structure with overlap slab is a new-type composite structure^[1-4]. Its concrete flange is combined with precast slab and in-situ concrete. The concrete and steel beams are tied together by using shear connectors. In this kind of structure, the advantages of steel and concrete material can be exerted respectively. Besides the characteristics of composite structure with in-situ concrete, it also has some other advantages such as saving form erecting processes and mould plates, quickening construction speed, decreasing of in-situ concrete and good comprehensive benefits^[5-12].

The behavior of steel-concrete composite bridge with overlap slab of long span is rather complex. So the difficulties in analysis are that the modeling of the whole and local mechanical properties of bridge, combining of precast slab and in-situ concrete, compositing of concrete and steel beam and the structure behavior under every construction phase. In the present study, the numerical method of steel-concrete composite structures with overlap slab was studied, and two-step finite element method was presented being applied to analyze an extra long span composite bridge.

There is a three span continuous steel through truss tied arch bridge with 177+428+177 m main bridge span. The composite deck with overlap slab, which consists of steel floor beam, precast slab and in-situ concrete, has been adopted in main span, as shown in Figs.1-3. The deck grid-beam system is consisting of steel longitudinal and transverse beams. Column headed shear studs of  22 mm in diameter on the top of steel beam and reinforced concrete deck slab form the composite beam structure. The dimensions of steel transverse beams are as follows. The top is of 700 mm in width and 20 mm in thickness, the bottom is of 1 000 mm in width and 20-50 mm in thickness and the webs are of 1 860-2 100 mm in width and 16 mm in thickness. The deck transverse slope is formed by changing web heights of steel transverse beams. There are 9 steal longitudinal beams in main arch deck. The outboard second steal longitudinal beam is main beam and others are subordinate beams. The height of main longitudinal beam is as same as transverse beams. The top of main longitudinal beam is of 400 mm in width and 20 mm in thickness, the bottom is of 800 mm in width and 20 mm in thickness and the webs are of 14 mm in thickness. The subordinate longitudinal beams are of 800 mm in height, their webs are of 1 400 mm in thickness, the top and bottom of them are 400 mm and 300 mm in width respectively and 20 mm in thickness. The deck consists of precast slab of grade C50 12 cm in thickness, 8 cm in thickness in-situ concrete, and medium modified bituminous concrete. The transverse joints between precast slabs are of 0.5 m in width, and longitudinal joints are of 0.3 m in width. The concrete filled in joints is compensating shrinkage steel fiber concrete of grade C50.

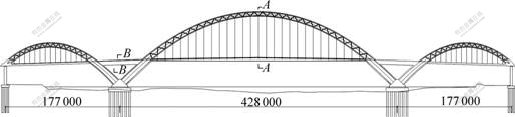
Fig.1 Overall layout of Xingguang bridge(Unit: mm)

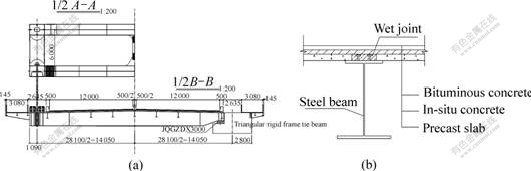
Fig.2 Transverse-section of bridge(a) and composite beam(b) (Unit: mm)

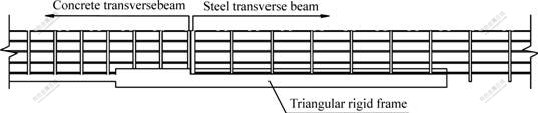
Fig.3 Collocation of longitudinal-transverse beam

The behavior of steel-concrete composite structure with overlap slab is closed related with construction processes. So, different modeling methods are needed for structure force in each phase^[13-14]. In order to exactly reflecting the whole and local mechanical properties of structure, it was analyzed using the two-step finite element method on the steel-concrete composite structure with overlap slab.

3.1 Construction methods and finite element model-ing

3.1.1 Construction method 1 and finite element modeling

Construction method 1: this project was proposed by the designer. The construction procedure is as follows. The precast slabs are first supported on the steel floor beam, and the construction joints are filled with concrete. The structure system is changed from simply support to continuous support after the concrete in construction joints reaches design strength, then in-situ concrete is cast. After the in-situ concrete reaches its design strength, the deck pavement will be done and the bridge can be used. There are three structure systems according to above construction procedure. System 1 is the system of floor beam in which the precast slabs are simply supported on the floor beam. Precast slabs only bear the deadweight of themselves. The deadweights of Precast slabs and construction joints are supported by steel floor beam. System 2, which bears the deadweight of in-situ concrete, is continuous composite system composed of precast slabs, construction joints and steel floor beam. System 3, which bears the deadweights of the deck pavement and live load, is continuous composite deck system composed of precast slabs, in-situ concrete and steel floor beam.

In this study, three different finite element models according to construction method 1, named G1, G2, and G3, were investigated.

1) The G1 model is a model that precast slabs supported on the steel floor beam with construction joints filled with concrete. But the concrete in construction joints has no force resistance before it reaches its design strength. It is just a load on steel floor beam. The precast slabs are simply supported on steel floor beam, and there are no composite actions between them. The stresses of precast slabs are produced by their deadweights. The steel floor beam supports the deadweights of precast slabs, construction joints and itself.

2) The G2 model was used to modeling the continuous composite system which composed of precast slabs, construction joints and steel floor beam, when the concrete in construction joints has force resistance after it reaches design strength. The deadweight of in-situ concrete is loaded on the deck of continuous composite system as uniformly distributed load.

3) The G3 model was proposed here to modeling the in-situ concrete, which has force resistance as it reaches its design strength, supports the actions of the live load, the loads of deck pavement and additional equipments.

3.1.2 Construction method 2 and finite element modeling

Construction method 2: Another project, proposed by the constructor for quickening construction plan, is that the top in-situ concrete and construction joint are cast at the same time. The precast slabs are first supported on the steel floor beam, then the in-situ concrete and construction joints are cast at the same time. After the in-situ concrete and construction joints reaches their design strength, the deck pavement is done and the bridge can be used. There are two structure systems according to the construction procedure. System 1 is the system of floor beam in which the precast slabs are simply supported on the floor beam with load of deadweight of in-situ concrete and construction joints. System 2, whose loads are the deadweights of the deck pavement and live load, is the continuous composite deck system composed of precast slab, in-situ concrete and steel floor beam. Comparing with construction method 1, the construction method 2 can save the time for waiting the construction joints reaching design strength and can quicken the construction plan.

Two different finite element models according to construction method 2, named H1 and H2, were studied.

1) The H1 model is a model of precast slab supported on the steel floor beam with in-situ concrete and construction joints being poured. But the in-situ concrete and construction joints have no force resistance as they have not reached design strength. They are only loads on steel floor beam. There is no composite action between precast slab and steel floor beam. The deadweights of in-situ concrete and construction joints directly act on floor beam. Stresses in precast slabs are produced by the deadweights of themselves and the in-situ concrete on them and the deadweights are transferred to the floor beam. The steel floor beam supports the deadweights of precast slabs, construction joints, and itself.

2) The H2 model is the same as G3 model in analysis according to designer’s construction method 1. The continuous composite deck system with overlap slab, which is composed of precast slabs, construction joints and steel floor beam, supports the actions of live load, the loads of deck pavement and additional equipments.

3.2 Two-step analysis method for general and local analyzing

The finite element analysis of the whole bridge is difficult to make the elements minute enough to reflect the working state of concrete in every layer of deck. But only analyzing of the deck can not accurately reflect the influence of the whole deformation of the bridge on the behavior of the deck. Therefore, there were actually two models, named (a) and (b), in every step of above construction methods and the models were calculated respectively.

Model (a) is the analysis of the whole bridge for finding out the vertical displacement at the end of every transverse beam which is produced by the whole deformation of the bridge. All of above is the preparation for the next step of calculation.

Model (b) analyzes the deck and takes the deck system as isolated body for calculation. The vertical displacements at the end of transverse beams calculated from first step is put on each end of every transverse beam in corresponding deck model as displacement constraint conditions for analysis.

The grids of the whole bridge model (Model (a)) are rough for the sake of reflecting the behavior of the whole bridge. The grids of the local deck model (Model (b)) are minute for describing the stress state of the concrete in the deck combined slab.

3.3 Elements, materials and loads

A general-purpose finite element software package ANSYS was used to model the whole bridge and local deck for elastic analysis. The arch ribs, web members, hangers and deck were modeled by space beam elements in the whole bridge model. The precast slabs and in-situ concrete slabs were modeled by space shell elements and the floor beam was modeled by space beam elements in the deck model. According to the plane section hypothesis, constraint equations were used to considerate the off-centre among longitudinal beams, transverse beams, and concrete slabs. The modulus of elasticity of steel is E_s=2.1×10⁵ MPa. Not considering the concrete creep, giving that the age of precast slab has four months, the modulus of elasticity of precast slab is E_c=3.73×10⁴ MPa, and modulus of elasticity of in-situ concrete is E_c=3.50×10⁴ MPa. The loads of deck system are shown as follows:

1) 1st-stage dead load: The deadweights of steel beams and precast slabs and construction joints(D₁₁), and the deadweight of in-situ concrete(D₁₂).

2) 2nd-stage dead load: Bituminous concrete of

0.184 t/m²+deadweights of deck pavement and additional equipments of 0.8 t/m²(D₂).

3) Live load: 6 lines automobile live load of grad

super 20 can be converted to uniformly distributed load of 0.288 t/m², it is 0.158 t/m²decreased by the discount coefficient of 0.55(L₁); and 6 lines automobile live load of grade super 20 is longitudinally and transversely, loaded as wheel press, with the transverse decrease coefficient of 0.55(L₂).

4.1 Stresses of concrete slabs

The stresses of concrete slabs by construction method 1 and construction method 2 under the total load of D₁₁+D₁₂+D₂+L₂ are shown in Table 1.

It can be seen from Table 1 that both calculation results of the two construction methods, either the construction method 1 proposed by the designer with in-situ concrete and construction joint being cast respectively, or the construction method 2 hoped by the constructor with in-situ concrete and construction joint being cast at one time, are that the stresses of precast slabs are greater than that of in-situ concrete slabs. It is dominated by the tension stresses at the bottom of precast slabs because the stresses produced by the 1st-stage dead load are greater. The construction method 1 has more advantages than construction method 2 for the concrete slabs. The transverse stresses at the bottom of precast slabs in construction method 2 exceed 3 MPa. The reason is that the precast slabs and steel floor beam become a composite system after the construction joints cast separately has reached the design strength. The negative bending moments of concrete slabs on steel floor beam, with the load of in-situ concrete slab’s deadweights, decrease the positive moments of concrete slabs in the center point of floor beam, and reduce the stresses of precast slabs accordingly.

4.2 Stresses of steel floor beam

The stress curves in the bottom flange of steel floor beam by construction methods 1 and 2 under the total load of D₁₁+D₁₂+D₂+L₂ are shown in Figs.4 and 5. The difference between the stresses of longitudinal beam by construction methods 1 and 2 is obvious, and the stress by construction method 1 is about 10.0 MPa less than that by construction method 2. The difference between the stresses of transverse beam is little. Here are the reasons: the difference of the two construction processes rests with the cast time of construction joints. The systems of precast slabs in construction methods 1 and 2 are different when the precast slabs bear the deadweight of in-situ concrete. It is a continuous system composed with floor beam in construction method 1 but a simply supported system on floor beam in construction method 2. So the decks of corresponding two construction processes are different in force. The precast slabs of this bridge can be seen as the one-way slabs. They are 3.0 m in width between two longitudinal beams and 12.0 m in width between two transverse beams. So that the mostly forces of precast slabs are first transferred to longitudinal beams, and then transferred to transverse beams. Only a little force is transferred to transverse beams directly. Therefore the influence of two different construction processes on longitudinal beams is greater than that on transverse beams. The construction method 1 has more advantages for the floor beam than the construction method 2.

                           Table 1 Total stresses of concrete slabs                        

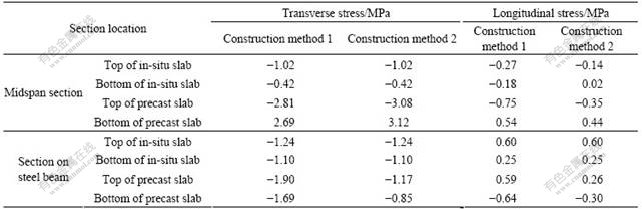
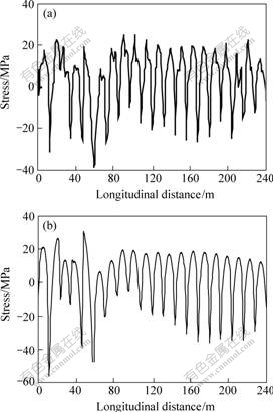
Fig.4 Distribution of stress on steel longitudinal beam

(a) Construction method 1; (b) Construction method 2

Fig.5 Distribution of stress of steel transverse beam

1) The mechanical behavior of steel-concrete composite structure with overlap slab is closed related with its construction program. The structure system of each corresponding construction phase is different in construction procedure. So, different modeling methods are needed to analyze in each phase respectively.

2) In large-scale complex structures, the finite element analysis of the whole structure is difficult to reflect the local force state. In order to exactly reflecting the force state of the whole bridge, a two-step finite element analysis method is used on the steel-concrete composite structure with overlap slab of long span bridge. It is applicable for analysis of other extra long span composite structures.

3) By comparing the stresses of the structure under two different construction methods, although the construction method that the top in-situ concrete and the concrete in construction joints being cast at the same time can shorten construction period, the construction method that the top in-situ concrete and the concrete in construction joints being cast respectively is more reasonable than the former for the decrease of the stresses in precast slabs and steel floor beam.

References

[1] LAM D, ELLIOTT K S, NETHERCOT D A. Parametric study on composite steel beams with precast concrete hollow core floor slab[J]. Journal of Constructional Steel Research, 2000, 54(2): 283-304.

[2] L??NE A, LEBET J P. Available rotation capacity of composite bridge plate girders under negative moment and shear[J]. Journal of Constructional Steel Research, 2005, 61(3): 305-327.

[3] YE Mei-xin, HUANG Qiong. Study of steel structure accidents[J]. Journal of the Changsha Railway University, 2002, 20(4): 6-10. (in Chinese)

[4] NAKAMURA S, MOMIYAMA Y, HOSAKA T, et al. New technologies of steel/concrete composite bridges[J]. Journal of Constructional Steel Research, 2002, 58(1): 99-130.

[5] YE Mei-xin, HUANG Qiong. Damage detection of high-speed railway steel-concrete composite beam[J]. Journal of Central South University: Science and Technology, 2005, 36(4): 704-709.(in Chinese)

[6] Brozzetti J. Design development of steel-concrete composite bridges in France[J]. Journal of Constructional Steel Research, 2000, 55(1/3): 229-243.

[7] HAENSEL J. Composite bridge design: The reanimation of steel bridge construction[J]. Journal of Constructional Steel Research, 1998, 46(1/3): 54-55.

[8] SHIM C S, LEE P G, CHANG S P. Design of shear connection in composite steel and concrete bridges with precast decks[J]. Journal of Constructional Steel Research, 2001, 57(3): 203-219.

[9] YE Mei-xin, ZHANG Ye-zhi . Behavior of steel-concrete composite beams under the action of negative moment[J]. China Railway Science, 2001, 22(5): 41-47.(in Chinese)

[10] MAR? A, MIRAMBELL E, ESTRADA I. Effects of construction process and slab prestressing on the serviceability behaviour of composite bridges[J]. Journal of Constructional Steel Research, 2003, 59(2): 135-163.

[11] RYU H K, CHANG S P. Ultimate strength of continuous composite box-girder bridges with precast decks[J]. Journal of Constructional Steel Research, 2005, 61(3): 329-343.

[12] YE Mei-xin, ZHANG Ye-zhi. Concrete–steel truss composite girder and shear connectors[J]. Journal of the China Railway Society, 1999, 21(1): 67-71.(in Chinese)

[13] LUO Ru-deng, YE Mei-xin. Study calculation of deflection of composite girders under action of negative moments[J]. China Railway Science, 2001, 22(5): 61-64. (in Chinese)

[14] ZHANG Ye-zhi­­. Analysis on responses of continuous composite beams in high-speed railways[J]. Journal of the China Railway Society, 2002, 24(6): 84-88. (in Chinese)

(Edited by YANG You-ping)

Foundation item: Project(2001G022) supported by the Science and Technology Development Program of Railways Department, China

Received date: 2006-05-12; Accepted date: 2006-07-21

Corresponding author: YE Mei-xin, Professor; Tel: +86-731-2656954; E-mail: yemx@mail.csu.edu.cn