Intelligent optimal control for lead-zinc sintering process state
来源期刊:中国有色金属学报(英文版)2006年第4期
论文作者:吴敏 徐辰华 杜玉晓
文章页码:975 - 981
Key words:lead-zinc sintering process; synthetical permeability; burn-through point(BTP); fuzzy expert controller; state- optimization control
Abstract: The intelligent integrated predictive model of synthetical permeability was established using the fuzzy classifier to combine the time sequence predictive model with the craftwork parameter predictive model. Then, the estimation model of burn-through point(BTP) based on pipe stress point(PSP) method and the predictive model of BTP were proposed. The optimal control of permeability and heat states was implemented by using the fuzzy expert controller with self-studying mechanism. The application of the intelligent control technique suppresses 17% of the fluctuation of synthetical permeability and 12% of the fluctuation of BTP, stabilizes the output and quality of sinter and settles the basis for the optimization of output and quality of sintering process.
基金信息:the National Natural Science Foundation of China

WU Min(吴 敏), XU Chen-hua(徐辰华), DU Yu-xiao(杜玉晓)
School of Information Science and Engineering, Central South University, Changsha, 410083, China
Received 3 Feburary 2005; accepted 5 April 2005
Abstract: The intelligent integrated predictive model of synthetical permeability was established using the fuzzy classifier to combine the time sequence predictive model with the craftwork parameter predictive model. Then, the estimation model of burn-through point(BTP) based on pipe stress point(PSP) method and the predictive model of BTP were proposed. The optimal control of permeability and heat states was implemented by using the fuzzy expert controller with self-studying mechanism. The application of the intelligent control technique suppresses 17% of the fluctuation of synthetical permeability and 12% of the fluctuation of BTP, stabilizes the output and quality of sinter and settles the basis for the optimization of output and quality of sintering process.
Key words: lead-zinc sintering process; synthetical permeability; burn-through point(BTP); fuzzy expert controller; state- optimization control
1 Introduction
The lead-zinc sintering process is an important step of imperial smelting process(ISP). It not only can agglomerate power materials, but also has pretreatment function of burning method for raw materials, so that the target of high productivity, high quality, low cost and longevity can be achieved in stove smelting[1]. The study of sintering process has attracted interest, not only in iron and steel industry, but also in nonferrous industry [2, 3].
The exhaust sintering technology is widely used in iron and steel smelting process. Many kinds of intelligent methods, such as fuzzy control, expert system, self-adaptive control and neural network, have been adopted in the iron and sintering process[4-6]. All these improved the level of automation control a great deal. However, there does not exist an industrial practical method of state modeling and optimal control of the sintering process. In the lead and lead-zinc smelting processes, the study of modeling mechanism and optimal control of the process is still in the first stage[7-13]. In 1980s, the methods of establishing various parameter model of ISP have been implemented in Hachinohe, Japan. They were used to control the water of sinters successfully according to the water content and permeability curve.
The state of sintering process mainly consists of permeability and heat states (also called temperature state), with the study focus of heat state on the prediction and control of burn-through point(BTP). They are connected with each other closely and are major elements for both the quantity and quality of sinter. Based on a lead-zinc smelting factory, the intelligent optimal control system of obturation blast sintering process focused on synthetical permeability was proposed, and the modeling and optimal control problem of an MIMO complex process was solved. Firstly, the configuration of the system and the idea of the permeability-based state-optimization control were presented. Secondly, the integrated predictive model of synthetical permeability based on time sequence and parameters was established through a fuzzy classifier. Meanwhile, fuzzy expert prediction of BTP was implemented. Thirdly, based on these models, the state-optimization control problem of sintering process is solved by using a fuzzy expert controller. Finally, the actual running results of the system were presented to demonstrate the validity of the method.
2 Brief review of sintering technology
The blast sintering process was often carried out in the dwight-lloyd(DL) type sintering machine, which was composed of 5 blowers: No.0 is igniting blower, No.1 and No.2 are fresh blowers, No.3 and No.4 returning-gas blowers, corresponding to 15 bellows. After the primary pile proportioning and the secondary conveyor scale proportioning, material passed the conditioner drum and the granulating drum, and became the blending material balls that have appropriate blending material water and chemistry components. Then, the blending material balls were sent to the ignition furnace and the main bin by a shuttle-distributor. In the ignition furnace, the blending material balls were spread around in the trolley of sintering machine to shape the thin bed material (3 cm), which was called ignition layer. By adjusting gas flux, appropriate ignition temperature was controlled to ignite the blending material on the ignition layer. After inflaming, the blending material moved with the trolley, and was combined with the newly added blending material to form the bed 30-40 cm in thickness in the back of sintering machine head. Due to the high sulfur content in blending material, heat released from the oxygenation reaction of sulfides made the reaction extend into the whole material layer, which assured the whole process of sintering and baking. The blending material moved with the trolley, and after 4 phases: evaporating, heating, reacting and sintering, the blending material balls become sintering agglomeration with certain structure, exceeded from the back of sintering machine. The 4 blowers provided oxygen in the oxygenation reaction to remove sulfur, and they also made necessary heat circulation possible. After two-level fragmentation of sintering agglomeration, the appropriate-sized sintering agglomeration entered smelting technology flow as sintering agglomerate, the rest used another two-level fragmentation to produce returning powder, and returned it to the secondary proportioning flow. The generated gas was educed by obturation hood for the manufacture of acid.
There are many factors related to the states of permeability and heat of sintering process. The traditional control methods based on a linear mathematic model cannot satisfy the practical requirements. So it is urgent to find a new method to solve the problems of process modeling and optimal control. The knowledge of sintering process often manifests as the form of experience rules and expert operation regulations. It is quite difficult to obtain many parameters with exact values. So, using fuzzy variables is appropriate to describe the process.
The authors invent a new method for modeling and optimal control of sintering process by utilizing intelligent methods, such as neural network, fuzzy control, and expert system. BTP is mainly decided by velocity and permeability and permeability state-optimization is the basis of heat state-optimization, so a state-optimization control method focusing on permeability is presented. First, predict and judge synthetical permeability. If permeability is not satisfactory, adjust ignition temperature and moisture of mixture to increase synthetical permeability exponent. If permeability is satisfactory with mini-fluctuation, then adjust velocity of trolley to stabilize BTP. Next, when big adjustments of material and/or operation parameters, or big exterior disturbances occur, first, permeability is optimized and stabilized, then BTP is stabilized.
3 Predictive model of synthetical permeabi- lity
3.1 Synthetical permeability exponent
The permeability of furnace burden refers to the volume of gas passed grate per square meter every second or the speed of gas, it can be counted by the resistance of material layer when a certain volume of gas in the unit area of grate passes material layer, which has a specific thickness, in a time unit. Due to the adoption of the obturation blasting sintering technology, according to the Voice formula[14], the permeability exponent of material in a given position of each bellow is
![]() (1)
(1)
where Pei refers to the permeability exponent, Qi is the volume of gas passed material layer per minute, m3/min; Fi is the area of convulsions, m2; h is the thickness of material layer, mm; Δpi is the resistance loss of material layer, Pa. In the lead-zinc obturation blasting sintering process, Qi and Fi are the gas volume and the area (a constant) of the ith branch bellow, respectively. The thickness of material layer seldom changes, and can be treated as a constant. The technology requests the “minute negative-pressure” state in the hood for sintering machine, in order to prevent gas from leaking to pollute environment. Since the resistance is very big when gas passes material layer and the pressure is very low after gas passes material layer, ![]() . So, the pressure of the branch of the ith bellow is taken as the pressure-loss of gas passing material layer, i.e.,
. So, the pressure of the branch of the ith bellow is taken as the pressure-loss of gas passing material layer, i.e., ![]() . n refers to the characteristic constant of gas. Before igniting and during the sintering process, n equals 0.6, and after sintering, n equals 0.55. At the same time of igniting, n equals 0.65. Since this paper focuses on permeability of material in the sintering process, n is chosen to be 0.6.
. n refers to the characteristic constant of gas. Before igniting and during the sintering process, n equals 0.6, and after sintering, n equals 0.55. At the same time of igniting, n equals 0.65. Since this paper focuses on permeability of material in the sintering process, n is chosen to be 0.6.
In order to have a comprehensive consideration of the influence of material permeability in different positions of different bellows on the whole permeability of sintering process, the concept of the synthetical permeability exponent to reflect the whole permeability of sintering process is given by
![]() (2)
(2)
where Pe1, Pe2 and Pei refer to permeability exponents of material corresponding to the different positions from No.1 to the ith bellows, λ1, λ2 and λi reflect the influence of permeability of material corresponding to the different positions from No.1 to the ith bellows on synthetical permeability exponent of sintering process. The combination of history data and expert experience gives
the restrict condition: ![]() .
.
Since No.10-No.15 bellows are the ones corresponding to No.1 returning blower, and it is impossible for them to get the flux data for the calculation of permeability exponent; only the permeability exponent of material of No.1-No.9 bellows can be obtained. However, in the practical process, the 4 phases of evaporation, heating, reacting, and sintering are mainly fulfilled in the No.1-No.9 bellows. So, the synthetical permeability exponent given by Eqn.(2) represents the whole permeability state of sintering process adequately.
3.2 Predictive model of synthetical permeability
Since history data contain the future information, time sequence can be taken into the prediction of the synthetical permeability, on the other hand, if many technology elements influencing permeability are taken into account, the prediction of synthetical permeability is implemented according to technology parameters. The time sequence model possesses high predictive precision under the stable condition. Otherwise, a big error occurs. Meanwhile, the technology parameter predictive model can achieve a comparatively satisfactory predictive result when state changes frequently. This paper proposes a coefficient-variable integrated predictive model of neural network, which combines time sequence prediction with technology parameter prediction appropriately so as to minish predictive error of the single model.
3.2.1 Time sequence predictive model
This model applies the back proragation neural network(BPNN) structure of a single-hidden layer: an input layer with 6 neurons, a hidden layer with 15 neurons and an output layer with 1 neuron. Pe(k)(x1) is defined to be current synthetical permeability exponent and Pe(k-1)(x2), Pe(k-2)(x3), Pe(k-3)(x4), Pe(k-4)(x5), Pe(k-5)(x6) are defined to be synthetical permeability exponents in above 5 moments. Pea(k+1) is defined to be synthetical permeability exponent in the next moment. Structure of this model is given by
![]() (3)
(3)
The structure of time sequence predictive model of synthetical permeability is:
![]() (4)
(4)
where ![]() is the weight of the signal from the jth neuron of the input layer to the ith neuron of the hidden layer,
is the weight of the signal from the jth neuron of the input layer to the ith neuron of the hidden layer, ![]() is the bias of the ith neuron of the hidden layer,
is the bias of the ith neuron of the hidden layer, ![]() is the weight of the signal from the i-th neuron of the hidden layer to the output layer, bO is the bias of the output neuron, tan sig(?) denotes the tan sig moid transfer function as
is the weight of the signal from the i-th neuron of the hidden layer to the output layer, bO is the bias of the output neuron, tan sig(?) denotes the tan sig moid transfer function as
![]() (5)
(5)
The neuro-network predictive model in this paper is similar to Eqn.(4).
3.2.2 Technology parameter predictive model
This model applies the BPNN structure of single-hidden layer: an input layer with 6 neurons, which are the inflame temperature (T0), the wet of the blending material (Rwater), the sulfur content of blending material (RS), the lead content of blending material (RPb), the silicon dioxide content of blending material (![]() ), the velocity of the trolley (V), a hidden layer with 15 neurons and an output layer with 1 neuron which is synthetical permeability exponent in the next moment (Peb(k+1)).
), the velocity of the trolley (V), a hidden layer with 15 neurons and an output layer with 1 neuron which is synthetical permeability exponent in the next moment (Peb(k+1)).
The technology parameter neuro-network predictive model of synthetical permeability is
![]() (6)
(6)
3.2.3 Coefficient-variable integrated predictive model of synthetical permeability
In order to synthesize the predictive result of time sequence and technology parameter prediction, the input variable set is classified and synthesized faintly by a fuzzy classifier to combine these models organically. The principle of a fuzzy classifier is, first, to classify the variables of state parameters faintly, and then, to evaluate stability function μA(x) of state parameters according to the method of calculating condition-membership function. μA(x) is defined to be the proportion of time sequence model. Its value range is [0, 1]. The bigger it is, the more stable the state is. [1-μA(x)] reflects the proportion of state parameter predictive model. A large value of [1-μA(x)] indicates a large fluctuation of the state. Under the condition of the small-changed state, the time sequence model is mainly obtained to be used to the prediction. Otherwise, the synthetical permeability model can be considered. Thus, predictive precision of the whole model is guaranteed.
The changes of state parameters are denoted by ΔRPb, ![]() …, ΔRwater. They are divided into three groups according to the proportion of sample numbers of every set in the whole samples, as shown in Fig.1 for ΔRPb. The region biases are respectively ±a1, ±a2, ±a3, and their values are decided by the condition of technology and history data, while membership function is given by
…, ΔRwater. They are divided into three groups according to the proportion of sample numbers of every set in the whole samples, as shown in Fig.1 for ΔRPb. The region biases are respectively ±a1, ±a2, ±a3, and their values are decided by the condition of technology and history data, while membership function is given by
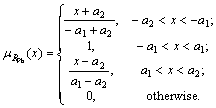 (7)
(7)
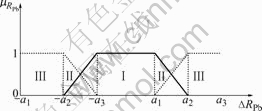
Fig.1 Fuzzy clustering of Pb content fluctuation
μA(x) is given by
![]() (8)
(8)
Therefore, the combined form of Eqns.(4) and (6) is
![]() (9)
(9)
It is used for the integrated predictive model of synthetical permeability.
4 Predictive model of BTP
For the sintering terminus, theoretically sulfid releases heat when it is heated to take the consuming oxygenation reaction, so that the position where the temperature of material surface is the highest corresponds to the position of sintering machine, i.e., the sintering terminus or BTP. The sintering terminus, as one of the criteria to judge the sintering process, reflects the burning state of material, and is the result of all kinds of elements influencing on one another. There are several methods to judge BTP: judge methods based on exhaust gas temperature or exhaust gas components, negative pressure method, predictive method, and BRP method [2].
During the obturation blasting sintering process of a specific lead-zinc smelting factory, 4 blowers corresponds to 15 bellows, with thermocouple to measure gas temperature in the position of each bellow. Operators estimate BTP according to the temperature curve obtained by thermocouple to adjust parameters. The measured temperature errors lead to the blind adjustment of parameters, carry out the heat state optimization of sintering process difficultly, accordingly, restrict the increase of quantity and quality of agglomerates. Therefore, it is urgently necessary to solve the problem of estimation and prediction of BTP.
4.1 Estimation of BTP
The position of BTP corresponds to the top of exhaust gas temperature measured by thermocouple theoretically, but thermocouple is only for the exhaust gas temperature, not for the material layer temperature. The position and depth of thermocouple affects the result directly. The industrial experiment on the distribution of temperature field of sintering machine is made to study the distribution rules of the exhaust gas temperature field in the flues for sintering machine. The result shows that the distribution of exhaust gas temperature field is not symmetrical, non-rules in the vertical change of the temperature field. The exhaust gas temperature only reflects the temperature of material layer surface roughly. The big error occurs when using the exhaust gas temperature to estimate BTP directly.
Study on the drang of branch canals of bellows in the whole sintering machine shows that the drang of branch canals takes on the trend of horizontal change: low→high→low→stabilization. In the phases of evaporation and heating, the drang of bellow branch canals is low and the permeability is satisfactory, but in the phases of reacting and sintering, since chemistry materials are melted and condensed to have oxygenation deoxidize reaction, the drang of bellow branch canals is high and permeability is not satisfactory. With the progress of sintering process, the drang of bellow branch canals falls rapidly, and holds the line when sintering process finishes. Thus, the position of BTP can be judged by the position of PSP after the drang of branch canals falls.
The position of PSP should be in accordance with normal BTP. Generally speaking, it lies on the position of the No.10 bellow, with the largest fluctuating range: No.8-No.14 bellows. The drang of branch canals of No.8-No.14 bellows is used to calculate the position of PSP. Some steps are as follows
Step 1: Calculate the change ratio of the horizontal drang
![]() (10)
(10)
Step 2: Estimate the point of toboggan of the horizontal drang according to the drang change ratio. If ?Pi, i+1>α (i=8, 9, ???, 13), it is estimated that the position of No.(i+1) bellow is the point of toboggan. α is constant decided by history data and expert experience, where, 0<α<1.
Step 3: Estimate PSP of the horizontal drang according to the drang change ratio. In step 2, we can find the point of toboggan of the horizontal drang. Suppose that it is No. n bellow, and if ![]() <β ( i =n, n+1, ???, 13), then the position of No.i bellow is considered PSP of the horizontal drang, that is to say, BTP lies on the position of No. i bellow, β is decided by history data and expert experience as a constant, where, 0<β<1.
<β ( i =n, n+1, ???, 13), then the position of No.i bellow is considered PSP of the horizontal drang, that is to say, BTP lies on the position of No. i bellow, β is decided by history data and expert experience as a constant, where, 0<β<1.
4.2 Prediction of BTP
The vertical sintering velocity of sintering raw materials and the horizontal velocity of trolley are decisive factors for the judge of BTP, moreover, permeability of sintering process is a key factor affecting vertical sintering velocity. The precise predictive value of BTP is not necessary, but the position of the bellow corresponding to the predictive value of BTP is available, so the satisfactory predictive result can be obtained through the model based on fuzzy expert rules. Some steps are as follows.
Step 1: Make the fuzzification of synthetical permeability and the velocity of the trolley (V). The value set of V is {NB (slower), NS (slow), ZO (moderate), PS (fast), PB (faster)}, and the value set of synthetical permeability Pe(k) is {NS(bad), ZO(good), PS (better)}. The current value of BTP is denoted as BTP
(k), and the next value of BTP is denoted as BTP (k+1).
Step 2: Predict the BTP using fuzzy expert rules. Some rules are:
Rule BTP 1: If BTP(k)=n , then BTP(k+1)=n;
Rule BTP 2: If Pe(k)=NS, then BTP(k+1)=BTP(k)+ 1;
Rule BTP 3: If Pe(k)=ZO, then BTP(k+1)=BTP(k);
Rule BTP 4: If Pe(k)=PS, then BTP(k+1)=BTP(k)- 1;
Rule BTP 5: If V=NB, then BTP(k+1)=BTP(k)-2;
Rule BTP 6: If V=NS, then BTP(k+1)=BTP(k)-1;
Rule BTP 7: If V=ZO, then BTP(k+1)=BTP(k);
Rule BTP 8: If V=PS, then BTP(k+1)=BTP(k)+1;
Rule BTP 9: If V=PB, then BTP(k+1)=BTP(k)+ 2;
Rule BTP 10: If BTP(k+1)>14, then BTP(k+1)=14;
Rule BTP 11: If BTP(k+1)<8, then BTP(k+1)=8.
5 State-optimization control of sintering process
The states of permeability and heat are two important factors to influence the output and quality of lead-zinc imperial sintering process. The state- optimization control of sintering process can stabilize the status, improve the productive and qualified rate. In this paper, the intelligent fuzzy expert controller with self-studying and self-adaptive ability that simulates human expert thought and decision-making method is adopted to solve some complex control problems.
The principle configuration of fuzzy expert controller is showed in Fig.2. It consists of database, reasoning machine, self-studying machine, rules database etc. Input parameters of the controller include predictive value of BTP, predictive value of synthetical permeability and actual technology parameters. Output parameters include ignition temperature, water content of raw material, and the velocity of trolley.
The operation principles of fuzzy expert controller are as follows.
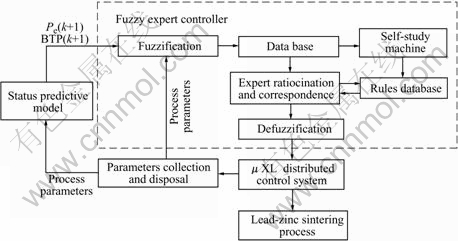
Fig.2 Principle frame of fuzzy expert controller
Step1: Determine the value set of input variables and make fuzzification according to the productive operation.
Step2: Make the fuzzy estimation of sythetical permeability. If synthetical permeability is not satisfactory, then use fuzzy expert rules for synthetical permeability to implement optimal control, next, shift to Step4. If synthetical permeability is satisfactory, then go to Step3.
Some fuzzy expert rules of synthetical permeability are:
Rule Pe 1: If permeability is not satisfactory and water content of material is high, then reduce water content of material.
Rule Pe 2: If permeability is not satisfactory and water content of material is low, then improve water content of material.
Rule Pe 3: If Pb, Si and S content of material are high or granularity is small, and water content of material is low, then lower ignition temperature and increase the velocity of trolley.
Rule Pe 4: If Zn content of material is high or granularity is big, and water content of material is high, then raise ignition temperature and increase the velocity of trolley.
…
Step3: Make the fuzzy estimation of BTP. The control parameter values are obtained by using corresponding fuzzy expert rules.
Rule BTP C 1: If BTP is ahead, then increase the velocity of trolley.
Rule BTP C 2: If BTP is appropriate, then retain the velocity of trolley.
Rule BTP C 3: If BTP is delayed, then reduce the velocity of trolley.
…
Step4: Make de-fuzzification for output variables to obtain the actual output of sintering process.
Self-studying mechanism can effectively enrich and modify rule databases, through on-line monitoring and evaluation for this control system and learning uncertain information of the plant, and improve some features of the whole control system.
6 Results of actual runs
3 000 group practical samples of a smelting factory are extracted from the database to be analyzed. Some actual results of the state predictive model for sintering process are shown in Fig.3. The dotted lines indicate that the predictive models of synthetical permeability and BTP have satisfactory predictive precision. The BTP data are some discrete digital points, and the value set is {8, 9, …, 14}. If the predictive value of BTP is not equal the actual value, then the prediction is wrong. In the practical control system, predictive error equals to 7.5%, which is obtained by the number of predictive error point divided by the number of the whole sample points. The average square error of the integrated predictive model of synthetical permeability is 0.006 8.
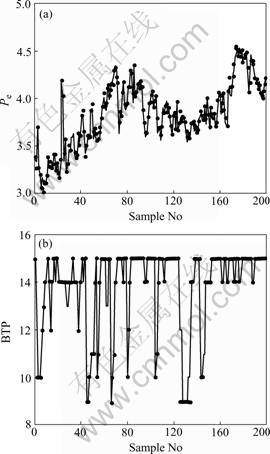
Fig.3 Results of actual runs of state predictive model
The results of actual runs show that due to applying state-optimization control of sintering process, it suppresses not only 17% of the fluctuation of synthetical permeability, but also 12% of the fluctuation of BTP, meanwhile, stabilizes the sintering state and set the basis for the optimization of output and quality of sintering process.
7 Conclusions
The authors propose the concept of synthetical permeability to describe sintering process, taking modeling and optimal control of the states of permeability and heat of lead-zinc sintering process as study background. The prediction of the synthetical permeability exponent is based on a combination of two predictive models of time sequence and technology parameter. Meanwhile, the estimation model of BTP through PSP method is proposed, and fuzzy expert rules are used to predict BTP. Based on state prediction of sintering process, the state-optimization control of process is implemented by using a fuzzy expert controller. The industrial model and the intelligent optimal control strategy of ISP are proposed for which makes the foundation for implementing synthetical optimal control of sintering process, at the same time, this intelligent integrated optimal control technique can be generalized to the field of iron and steel sintering process.
References
[1] The Group of Editors of the Reference Design Manual of the Smelting of Cu, Pb and Zn. The Reference Design Manual of the Smelting of Cu, Pb and Zn [M]. Beijing: Metallurgical Industry Press, 1979. 129-133.
[2] WANG Hai-dong, QIU Guan-zhou, HUANG Sheng-sheng. Advances in control techniques of sintering process [J]. Mining and Metallurgical Engineering, 1999, 19(3): 3-6.
[3] XIE Liang-xian. Development of automatic control technology for agglomeration process [J]. Metallurgical Industry Automation, 1994, 18(6): 7-11.
[4] JIANG Hong-zhou, ZHANG Xue-dong, ZHONG Hong-xun, et al. A real-time expert instruction system for sinter production [J]. Sintering and Pelletizing, 2000, 25(1): 8-10.
[5] XI An-min, LIU Xiao-Chao, LIU Ying. Developed the fuzzy control of sintering burning-through-point [J]. Metallurgical Equipment, 2000, 1: 19-21.
[6] LI Tao, FAN Xiao-hui, JIANG Tao, et al. Adaptive prediction of sinter burning through point based on heat pattern parameters [J]. Sintering and Pelletizing, 2000, 25(2): 1-3.
[7] ZHANG Le-ru. Research and practice of updraught sintering technique for lead concentrate [J]. Hunan Nonferrous Metals, 1999, 15(4): 18-21.
[8] WANG Yi-wen, GUI Wei-hua, WANG Ya-lin. Integrated model for predicting burning through point of sintering process based on optimal combination algorithm [J]. The Chinese Journal of Nonferrous Metals, 2002, 12(1): 191-195.(in Chinese)
[9] LIU Yu-chang, GUI Wei-hua, ZHOU Zi-min. Study on intelligent control of BTP based on soft-sensor technology [J]. Sintering and Pelletizing, 2002, 27(3): 27-30.
[10] DU Yu-xiao, WU Min, GUI Wei-hua, et al. The neural network model of permeability of lead & zinc smelting process based on chaotic optimization genetic algorithm [A]. Process Control Science Technology and Applications [C]. Guangzhou: South China University of Technology Press, 2002. 205-209.
[11] WANG Yao-nan, WANG Hui, PENG Jian-chun, et al. Synthetic intelligent control system for complex industrial process [J]. Information and Contrl, 1999, 28(4): 298-304.
[12] WU Min, SHE Jin-hua, NAKANO M. An expert control system using neural networks for the electrolytic process in Zinc hydrometallurgy [J]. Engineering Applications of Artificial Intelligence, 2001, 14(5): 589-598.
[13] WU Min, SHEN De-yao. Expert control based on neural networks and mathematical models for the coal blending process [J]. Control theory and application, 2000, 17(6): 868-872.
[14] ZHOU Qu-ding, KONG Ling-tan. The Theory and Technology of Iron Ore Agglomeration [M]. Beijing: Metallurgical Industry Press, 1989.
Foundation item: Project(60425310) supported by the National Natural Science Foundation of China; Project supported by the Teaching and Research Award Program for Outstanding Young Teachers in Higher Education Institutions of Ministry of Education of China
Corresponding author: WU Min; Tel: +86-731-8836091; E-mail: min@csu.edu.cn

