­­ Numerical simulation of temperature field in plasma-arc flexible forming of laminated-composite metal sheets

SONG Wen-qing(宋文庆)¹, XU Wen-ji(徐文骥)¹, WANG Xu-yue(王续跃)¹,

MENG Jian-bing(孟建兵)¹, LI Hong-you(李洪友)²

1. School of Mechanical Engineering, Dalian University of Technology, Dalian 116024, China;

2. College of Mechanical Engineering and Automation, Huaqiao University, Quanzhou 362021, China

Received 2 March 2009; accepted 30 May 2009

Abstract: Flexible forming of laminated-composite metal sheets (LCMS) using plasma arc is a latest technique, which produces LCMS components by thermal stress without mould and external force. Considering that the controllable temperature field is the key during the forming process, a three-layer FEM model, based on the characteristics along LCMS thickness direction, was developed to study the variation rules of temperature field, which was verified robustness by experimental validation. Besides, the influences of process parameters such as plasma arc power, scanning speed and plasma arc diameter on LCMS temperature field were performed. The comparisons of LCMS with single layer metal sheet (SLMS) show the temperature difference of LCMS along thickness direction is smaller than that of SLMS, but the heat-affected zone of LCMS along X axis is wider than that of SLMS under the same process parameters.

Key words: laminated-composite metal sheets; plasma arc forming; temperature field; numerical simulation

1 Introduction

Laminated-composite metal sheets (LCMS) such as stainless steel/carbon steel have the comprehensive advantages of good performance and low price, which can be used as the alternative materials of integral stainless steel with the superiority of reducing the manufacturing cost and saving precious metals[1]. Usually, many kinds of moulds and dies are needed according to the desired shape of LCMS products, which costs lots of time and money. Hence, there is a crucial signification to develop a LCMS flexible forming technique without mould and die, which will cut down the cost, shorten the period of developing a new product, and promote the wider application of LCMS.

Flexible forming using plasma arc (FFUPA) is a newly developed technique, which produces deformation in metal sheet by thermal stress instead of external mechanical force. Without the requirement of mechanical contact, and hence without the need for hard tooling, it can significantly decrease the high cost and long time associated with the production of component specific tooling[2]. Furthermore, plasma arc has the advantages of higher power density, better controllability, stronger environment adaptability and lower cost[3]. Therefore, the technology of FFUPA has a bright development prospect especially in economically producing prototype or small batch of sheet type components in engineering metals. MALE et al[2] firstly demonstrated the feasibility of FFUPA in 2000, then investigated the correlations between process parameters and bending angles of mild steel and stainless steel sheets during line heating, and studied the microstructural development in the heat affected zone[2-5]. Based on the combination of experiments and numerical simulation, XU et al[6-11] conducted a systematical research on the forming mechanism, the rules of FFUPA affected by process parameters and material properties and scanning trajectory. WANG et al[12-13] studied the relationship between main process parameters and bending forming through experiments using the metal sheets of 1Cr18Ni9Ti and Q235.

However, the investigations on FFUPA mainly focus on single-layer metal sheet (SLMS), and there is less public literature on the flexible forming of LCMS using plasma arc. Compared with the more homogeneous distribution of SLMS compositions, the distribution of the compositions along LCMS thickness direction is non-uniform due to the combined interface. Subsequently, the failures such as delamination of combined interface, wrinkling and spalling of clad layer, may appear. Furthermore, material physical parameters varying with temperature play a key role during FFUPA[7, 11], and the characteristics of sharp changes of physical parameters along LCMS thickness direction will have a significant influence on the forming process. Besides, thermal stresses in FFUPA are induced by uneven temperature field which occurs due to the irradiating from plasma arc scanning. Therefore, it is very significant to understand the distribution of temperature field in LCMS so as to control the forming process and avoid forming failures.

In this work, a three-layer FEM model of FFUPA of LCMS has been developed, considering the characteristics along LCMS thickness direction. The numerical simulation software ANSYS was applied in the analysis of the temperature field during plasma arc forming of representative LCMS (Q235A/1Cr13) and SLMS (Q235A), respectively. Through the comparison of experiments with numerical simulation, the distribution rules of LCMS temperature field were further understood, and provided a theoretical guidance for the analysis of deformation field and the improvement of LCMS forming quality.

2 Fundamentals

2.1 Principle of FFUPA

As shown in Fig.1, when the scanning path and speed of plasma arc are properly controlled with assisted cooling stream, uneven temperature field, which leads to thermal stress, occurs in metal sheet. Once the thermal stress goes beyond the material yield limit at corresponding temperature, expectable bending forming can be obtained due to the plastic deformation of metal sheet without mould and external force.

Fig.1 Schematic diagram of FFUPA

2.2 Simulation theory of temperature field

In the simulation of FFUPA, the thermal load is given in the form of thermal flux density, which obeys a Gaussian distribution as follows:

                  (1)

where P_r is the thermal flux density of plasma arc, P is plasma arc power, d is the diameter of nozzle, and r is the distance from the center of the plasma arc.

For the thermo-mechanical coupled system, the thermal equilibrium equation for the analysis of heat transfer can be written as

                (2)

where ρ and с are density and specific heat of the material, respectively, k is heat conductivity and  is the rate of heat generation. Here,  is mainly considered as the heat source from plasma arc scanning.

To solve the thermal equilibrium equation, boundary conditions and initial conditions need to be introduced. The basic FEM equation for thermal problem can be derived from the thermal equilibrium equation.

                       (3)

where  is the heat capacity matrix, [N] is the shape function matrix,  is the heat conduction matrix,

{T} and {} are nodal temperature vector and nodal temperature rate vector, respectively, {B} is the general geometric matrix, and {Q} is the heat flux vector.

3 Modeling

3.1 Meshing grids

Under the coordinate of Cartesian, the FEM model of LCMS, based on the characteristics of combined interface and sharp changes of material physical properties along LCMS thickness direction, was established, as shown in Fig.2, which included three layers: base layer, transition layer and clad layer. Moreover, to ensure calculation precision and save computational time, transitional meshing method was applied in the model which was divided into three zones along X axis: A zone (the heating zone), B zone (the transition zone) and C zone (the rest zone). The grids in zone A were finer than the other zones.

Fig.2 Half of FEM model

3.2 Material physical properties

In this work, the three-layer FEM model of LCMS (Q235A/1Cr13) included base layer (Q235A), clad layer (1Cr13) and transition layer. Materials in each layer  were presumed as homogeneous and isotropic, and the material physical parameters merely changed with temperature. Tables 1 and 2 list the chemical compositions and the physical properties of Q235A and 1Cr13 varying with temperature[14], respectively. The physical properties of transition layer were calculated by interpolation method.

3.3 Boundary conditions

The room temperature (25 ℃) was considered as the initial temperature of metal sheet which was cooled naturally after plasma arc heating. There are convection and radiation between the metal sheet and ambient environment, and can be written as follows with respect to the heat transfer[11]:

                          (4)

where α is heat transfer coefficient, t is surface temperature of metal sheet, and t₀ is the temperature of ambient environment.

Table 1 Chemical compositions of Q235A and 1Cr13 (mass fraction, %)

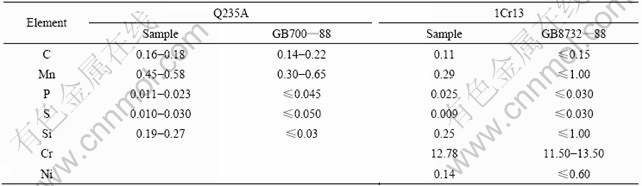
Table 2 Physical properties of Q235A and 1Cr13 varying with temperature

4 Results and discussion

In this work, LCMS (Q235A/1Cr13) and SLMS (Q235A) were selected as the samples with 100 mm in length, 80 mm in width (along plasma-arc scanning direction), and 2 mm in thickness along which it was divided into three layers: base layer (Q235A) of 1 mm, transition layer of 0.4 mm, and clad layer (1Cr13) of 0.6 mm[15]. Plasma arc was scanned on the surface of base layer (Q235A). The scanning trajectory was parallel to Z axis and in the middle of metal-sheet length. To compare LCMS with SLMS, the same meshing methods of geometric model were adopted by SLMS. The diameter of nozzle is 2 mm. Here, P is plasma arc power, v is plasma arc scanning speed, d is the diameter of plasma arc on the surface of metal sheet, and t is time.

4.1 Experimental validation for FEM model

To verify the FEM model, HSM-673 infrared radiation thermometer (the diameter of minimum target is 0.5 mm, D?S=145?1, measurement range of temperature is from 200 to 1 650 ℃) was adopted to measure the temperature variations of the points on the LCMS bottom surface (1Cr13), which were 0, 2, and 4 mm from the centerline, respectively (Fig.3).

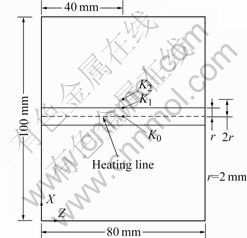
Fig.3 Locations of measurement in experiments

Figs.4-6 show temperature variations of the three points, separately. It can be seen that the FEM model predicts temperature well, especially for the point near the heating line. For points far away from the heating line, the errors increase because of the effect of finite width of the LCMS. Since the plastic deformation is confined in a narrow region near the heating line, the error in temperature far away from the heating line will not have large effect in prediction of the bending angle. Therefore, the FEM model can be used to compute and predict the distribution of temperature field during FFUPA of LCMS.

Fig.4 Temperature variations at K₀ (x=0 mm) (P=500 W, v=   4 mm/s, d=4 mm)

Fig.5 Temperature variations at K₁ (x=2 mm) (P=500 W, v=   4 mm/s, d=4 mm)

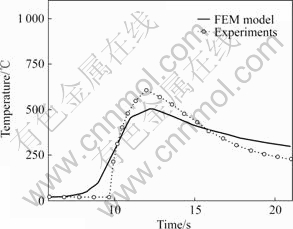
Fig.6 Temperature variations at K₂ (x=4 mm) (P=500 W, v=   4 mm/s, d=4 mm)

4.2 Temperature field comparison of LCMS with SLMS

Figs.7-9 show the temperature distributions of LCMS and SLMS, respectively. Here, Y₂ (50, 2, 40), Y₁ (50, 1, 40), Y_0.6 (50, 0.6, 40) and Y₀ (50, 0, 40) are the nodes in different layers of metal sheet, respectively.

Fig.7 Temperature variations of Y₀ and Y₂ (P=400 W, v=8 mm/s, d=4 mm)

Fig.8 Variations of temperature difference between Y₀ and Y₂  (P=400 W, v=8 mm/s, d=4 mm)

Fig.9 Distributions of temperatures through Y₀ and Y₂ (a), Y_0.6 and Y₁ (b) along X axis (P=400 W, v=8 mm/s, d=4 mm, t=5.5 s)

Fig.7 shows the temperature distributions of Y₀ and Y₂ with time. It is indicated that the temperature variations of LCMS are similar with those of SLMS. When plasma arc is far away from Y₂, there is no significant changes of temperature at Y₂ and Y₀, and this is the preheating stage (P stage) of FFUPA. With the plasma arc moving nearer, the temperatures of the two nodes increase sharply when t is 4.6 s. However, the temperature increase of Y₂ is faster than that of Y₀ due to heat transfer. Consequently, the temperature difference between the two nodes rises quickly. When t is 5.5 s, the node temperature and temperature difference reach the maximum. With the plasma arc moving away, the temperature of Y₂ decreases rapidly, and the temperature of Y₀, however, rises first, then decreases slowly for the reason of the heat transfer from high temperature region and the heat exchange with ambient environment. The temperature difference decreases to zero when t is 6 s. This is the variation stage of temperature difference (D

stage). Thereafter, the temperatures of the two nodes decrease slowly to ambient temperature due to the high energy injection of plasma arc, and it seems a “tail” (T stage). Since the temperature difference along thickness direction of metal sheet leads to thermal stress, which causes the material plastic deformation[16]. It can be concluded that D stage is the main stage of LCMS deformation.

Fig.8 shows the variations of temperature difference between Y₀ and Y₂ with time. It can be seen that the variation of temperature difference of LCMS is gentler than that of SLMS, and the value of LCMS is smaller than that of SLMS.

Figs.9(a) and (b) illustrate the distributions of node temperatures in different layers along X axis when t=  5.5 s. It is noted that the temperature distributions of LCMS are the same as those of SLMS on top layer (y=2 mm) and the second layer (y=1 mm). While the temperature values on the third layer (y=0.6 mm) and the bottom layer (y=0 mm) are different. It can also be seen that the heat affected zones of LCMS along X axis in bottom layer and third layer are wider than those of SLMS (H_L-0＞H_S-0, H_L-0.6＞H_S-0.6). The reason is that the thermal conductivity of 1Cr13 is smaller than that of Q235A, but the specific heat of 1Cr13 is much smaller than that of Q235A at the same temperature, thus, the temperature of 1Cr13 is higher than that of Q235A when the heat input from plasma arc is same.

4.3 Effects of plasma arc process parameters on temperature field of LCMS

During FFUPA, the important premise is that the temperature on top surface of metal sheet reaches a certain critical value that leads to the occurrence of material plastic deformation, and the temperature difference along thickness direction is the main factor that decides the deformation of metal sheet. Therefore, the peak temperatures on top and bottom surfaces and temperature difference along thickness direction of metal sheet are chosen as the evaluation factors. Figs.10-12 show the variations of peak temperature and temperature difference between nod Y₂ (50, 2, 40) and node Y₀ (50, 0, 40) affected by plasma arc power P, scanning speed v, and plasma arc diameter d, respectively.

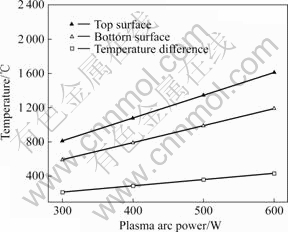
Fig.10 Effect of plasma arc power on peak temperature (v=   4 mm/s, d=4 mm)

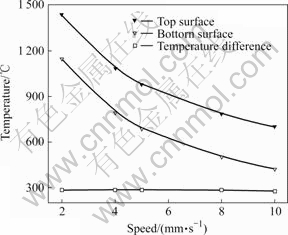
Fig.11 Effect of plasma arc scanning speed on peak temperature (P=400 W, d=4 mm)

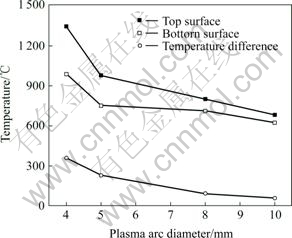
Fig.12 Effect of plasma arc diameter on peak temperature (P=500 W, v=4 mm/s)

From Fig.10, it can be seen that the peak temperature and temperature difference increase linearly with the increase of plasma arc power. The reason is that the power density irradiating on LCMS top surface increases with the increase of plasma arc power, and it takes time for heat to transfer from top surface to bottom surface. Consequently, the temperature of Y₂ rises faster than that of Y₀.

Fig.11 indicates the effect of plasma arc scanning speed on the peak temperature and temperature difference. With the increase of scanning speed, the energy absorption of LCMS reduces because of the short time heating from plasma arc. Therefore, the peak temperatures of Y₂ and Y₀ decrease when plasma arc scanning speed increases. Besides, there is no significant change of temperature difference between the two nodes with the variation of scanning speed.

Fig.12 shows the variations of peak temperature and temperature difference with plasma arc diameter. It can be seen that the peak temperature of Y₂ decreases faster than that of Y₀ with the increase of plasma arc diameter, accordingly, the temperature difference between the two nodes reduces. This is because that the power density irradiated by plasma arc decreases with the increase of plasma arc diameter.

For specified LCMS, the comprehensive analysis shows that the forming efficiency can be improved by properly increasing plasma arc power and scanning speed, and decreasing plasma arc diameter under the condition that the material properties are not destructed.

5 Conclusions

A three-layer FEM model of FFUPA was developed, considering the characteristics of LCMS. The temperature field comparisons of LCMS (Q235A/1Cr13) with SLMS (Q235A) were performed through numerical simulation. The main conclusions are as follows:

1) The variations of temperature fields of LCMS and SLMS both include P stage, D stage and T stage, and D stage is the main stage of the metal sheet forming. Besides, the temperature difference of LCMS along thickness direction is smaller than that of SLMS, but the heat-affected zone of LCMS along X axis is wider than that of SLMS under the same process parameters.

2) The temperature difference along LCMS thickness direction increases linearly with the increasing of plasma arc power, and decreases when plasma arc diameter increases. However, there is no significant change of temperature difference with the variation of plasma arc scanning speed.

3) The comparisons of calculated values with experimental results show the robustness of the developed model, and the simulation results can provide reference for further stress analysis and forming control.

References

[1] KHODADAD MOTARJEMI A, KOCAK M, VENTZKE V. Mechanical and fracture characterization of a bi-material steel plate [J]. International Journal of Pressure Vessels and Piping, 2002, 79: 181-191.

[2] LI P J, CHEN Y M, MALE A T, ZHANG Y M. Flexible forming of sheet metal using a plasma arc [J]. Journal of Engineering Manufacture, 2000, 214: 117-125.

[3] MALE A T, PAN C, CHEN Y W, LI P J, ZHANG Y M. Processing effects in plasma forming of sheet metal [J]. Annals of the CIRP, 2000, 49(1): 213-216.

[4] PAN C X, CHEN Y W, MALE A T. Microstructural development in plasma jet forming of sheet steels [J]. Materials Science and Technology, 2002, 18: 1151-1155.

[5] MALE A T, CHEN Y W, PAN C, ZHANG Y M. Rapid prototyping of sheet metal components by plasma-jet forming [J]. Journal of Materials Processing Technology, 2003, 135: 340-346.

[6] XU Wei-ji, WANG Tao, FANG Jian-cheng, QU Hong-wei, LIU Fei. An experimental study on flexible forming of sheet metal using plasma arc [J]. China Mechanical Engineering, 2004, 15(23): 2146-2149. (in Chinese)

[7] XU W J, WANG T, FANG J C, QU H W, LIU F, ZHAO Z Y. A numerical simulation of temperature field in plasma-arc forming of sheet metal [J]. Journal of Materials Processing Technology, 2005, 164/165: 1644-1649.

[8] XU W J, FANG J C, PANG G B. An experimental study on 3D forming of sheet metal using plasma arc [J]. Materials Science Forum, 2005, 475/479: 3943-3946.

[9] XU W J, FANG J C, LIU F, WANG X Y, ZHAO Z Y. Application of neural network in plasma-arc flexible forming [J]. Key Engineering Materials, 2005, 291/292: 615-618.

[10] WU W B, XU W J, WANG Z Y, ZHOU J J. Technology and study on circular arc flexible forming of sheet metal using plasma arc [J]. Materials Science Forum, 2006, 532/533: 508-618.

[11] WU W B, XU W J, WANG Z Y, ZHOU J J. Analysis of edge effects on flexible forming of sheet metal using plasma arc [J]. International Journal of Manufacturing Technology and Management, 2008, 13(2): 254-264.

[12] WANG Yang, WANG Mao-lu, HU Xi, WU Xiao-feng. The experimental study on flexible forming of sheet metal using plasma arc [J]. Journal of Shanghai Jiaotong University, 2006, 40(10): 1694-1698. (in Chinese)

[13] WANG M L, YANG L J, WANG Y. Investigation on the mechanisms of flexible sheet metal forming using plasma arc [J]. Materials Science Forum, 2006, 532/533: 93-96.

[14] Editorial Board of Mechanical Engineering Handbook of Material Performance. Mechanical engineering handbook of material performance. Materials properties handbook [M]. Beijing: Mechanical Industry Publishing House, 1995. (in Chinese)

[15] ZENG Zheng-ming. Mechanical engineering material handbook [M]. Beijing: Mechanical Industry Publishing House, 2003. (in Chinese)

[16] CHEN D J, WU S C, LI M Q. Deformation behaviors of laser curve bending of sheet metals [J]. Journal of Materials Processing Technology, 2004, 148: 30-34.

Foundation item: Projects(50775019, 50675072) supported by the National Natural Science Foundation of China; Project(20062178) supported by the Natural Science Foundation of Liaoning Province, China

Corresponding author: WANG Xu-yue; Tel: +86-411-86929050; E-mail: wbzzd@dlut.edu.cn

(Edited by YANG You-ping)