Effects of different numerical algorithms on simulation of chemical dissolution-front instability in fluid-saturated porous rocks
来源期刊:中南大学学报(英文版)2018年第8期
论文作者:赵崇斌 Bruce HOBBS Alison ORD
文章页码:1966 - 1975
Key words:numerical algorithm; chemical dissolution; front instability; computational simulation; porous rocks
Abstract: Many scientific and engineering problems need to use numerical methods and algorithms to obtain computational simulation results because analytical solutions are seldom available for them. The chemical dissolution-front instability problem in fluid-saturated porous rocks is no exception. Since this kind of instability problem has both the conventional (i.e. trivial) and the unconventional (i.e. nontrivial) solutions, it is necessary to examine the effects of different numerical algorithms, which are used to solve chemical dissolution-front instability problems in fluid-saturated porous rocks. Toward this goal, two different numerical algorithms associated with the commonly-used finite element method are considered in this paper. In the first numerical algorithm, the porosity, pore-fluid pressure and acid/solute concentration are selected as basic variables, while in the second numerical algorithm, the porosity, velocity of pore-fluid flow and acid/solute concentration are selected as basic variables. The particular attention is paid to the effects of these two numerical algorithms on the computational simulation results of unstable chemical dissolution-front propagation in fluid-saturated porous rocks. The related computational simulation results have demonstrated that: 1) the first numerical algorithm associated with the porosity-pressure-concentration approach can realistically simulate the evolution processes of unstable chemical dissolution-front propagation in chemical dissolution systems. 2) The second numerical algorithm associated with the porosity-velocity-concentration approach fails to simulate the evolution processes of unstable chemical dissolution-front propagation. 3) The extra differential operation is the main source to result in the failure of the second numerical algorithm.
Cite this article as: ZHAO Chong-bin, Bruce HOBBS, Alison ORD. Effects of different numerical algorithms on simulation of chemical dissolution-front instability in fluid-saturated porous rocks [J]. Journal of Central South University, 2018, 25(8): 1966–1975. DOI: https://doi.org/10.1007/s11771-018-3887-4.

J. Cent. South Univ. (2018) 25: 1966-1975
DOI: https://doi.org/10.1007/s11771-018-3887-4
ZHAO Chong-bin(赵崇斌)1, Bruce HOBBS2, Alison ORD2
1. Computational Geosciences Research Centre, Central South University, Changsha 410083, China;
2. School of Earth and Environment, The University of Western Australia, Crawley, WA 6009, Australia
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract: Many scientific and engineering problems need to use numerical methods and algorithms to obtain computational simulation results because analytical solutions are seldom available for them. The chemical dissolution-front instability problem in fluid-saturated porous rocks is no exception. Since this kind of instability problem has both the conventional (i.e. trivial) and the unconventional (i.e. nontrivial) solutions, it is necessary to examine the effects of different numerical algorithms, which are used to solve chemical dissolution-front instability problems in fluid-saturated porous rocks. Toward this goal, two different numerical algorithms associated with the commonly-used finite element method are considered in this paper. In the first numerical algorithm, the porosity, pore-fluid pressure and acid/solute concentration are selected as basic variables, while in the second numerical algorithm, the porosity, velocity of pore-fluid flow and acid/solute concentration are selected as basic variables. The particular attention is paid to the effects of these two numerical algorithms on the computational simulation results of unstable chemical dissolution-front propagation in fluid-saturated porous rocks. The related computational simulation results have demonstrated that: 1) the first numerical algorithm associated with the porosity-pressure-concentration approach can realistically simulate the evolution processes of unstable chemical dissolution-front propagation in chemical dissolution systems. 2) The second numerical algorithm associated with the porosity-velocity-concentration approach fails to simulate the evolution processes of unstable chemical dissolution-front propagation. 3) The extra differential operation is the main source to result in the failure of the second numerical algorithm.
Key words: numerical algorithm; chemical dissolution; front instability; computational simulation; porous rocks
Cite this article as: ZHAO Chong-bin, Bruce HOBBS, Alison ORD. Effects of different numerical algorithms on simulation of chemical dissolution-front instability in fluid-saturated porous rocks [J]. Journal of Central South University, 2018, 25(8): 1966–1975. DOI: https://doi.org/10.1007/s11771-018-3887-4.
1 Introduction
Instability of chemical dissolution fronts in fluid-saturated porous media has attracted ever-increasing attention in a wide range of scientific and engineering communities [1–10]. The main forces to drive the continuing study of the chemical dissolution-front instability can be described as follows. First, ever-increasing demand on the consumption of natural minerals requires us to find large mineral resources in the deep Earth, so that we cannot help but understand the controlling dynamic mechanisms of ore-forming processes in a much better way. Since pore-fluid flow is the main carrier to transport minerals from the lower crust into the upper crust of the Earth, the chemical dissolution-front instability, which can create the preferential flow channels in porous rocks, may become one of the controlling dynamic mechanisms of ore-forming processes within the crust of the Earth [11]. Second, ever-increasing demand on the consumption of energy resources requires us to increase the production of crude oils from oil reservoirs that are located in the deep Earth, so that we should develop innovative technologies through better understanding the behaviors of acidization dissolution-front instability in fluid-saturated carbonate rocks [12–17]. Third, CO2 sequestration in the deep geological strata is an effective method to reduce the green house effect. However, CO2 may react with water to form carbonic acid (i.e. H2CO3). This acid can further dissolve the dissolvable minerals of porous rocks, so that chemical dissolution fronts may be formed in the deep geological strata. If the resulting chemical dissolution fronts are unstable, they may create the preferential flow channels in the porous rocks. Once such preferential flow channels penetrate the deep geological strata, the stored CO2 may leak from the deep geological strata into underground water systems, leading to the contamination of the underground water [18–20]. Therefore, from the geoenvironmental point of view, the study of the chemical dissolution-front instability is also an important topic in the field of hydrogeology.
Many scientific and engineering problems need to use numerical methods and algorithms to obtain computational simulation results because analytical solutions are seldom available for them. The chemical dissolution-front instability problem in fluid-saturated porous rocks is no exception. Since this kind of instability problem has both the conventional (i.e. trivial) solution and the unconventional (i.e. nontrivial) solution, it is necessary to examine the effects of different numerical algorithms on the computational simulation results of chemical dissolution-front instability problems. Currently, there are two different algorithms for dealing with chemical dissolution-front instability problems in fluid- saturated porous rocks. In the first numerical algorithm, the porosity, pore-fluid pressure and acid/solute concentration are selected as basic variables, so that it is labeled the φ–p–C approach algorithm. However, in the second numerical algorithm, the porosity, velocity of pore-fluid flow and acid/solute concentration are selected as basic variables, so that it is labeled the φ–u–C approach algorithm. Compared with the φ–u–C approach algorithm, the φ–p–C approach algorithm has a smaller number of independent variables in the governing partial differential equations. This means that the φ–p–C approach algorithm is computationally superior to the φ–u–C approach algorithm in dealing with chemical dissolution-front propagation problems in fluid-saturated porous rocks.
Although both the φ–p–C approach algorithm and the φ–u–C approach algorithm can produce the same computational simulation results for a chemical dissolution-front propagation problem when the chemical dissolution system is in a subcritical state, no research has been conducted to examine the overall behavior of the φ–u–C approach algorithm when it is used to simulate chemical dissolution-front propagation in supercritical chemical dissolution systems. Therefore, it is natural to fill this gap by conducting such research. The outcome of this study will answer the following realistic question: how can different numerical algorithms affect the computational simulation results of a chemical dissolution front propagation problem in fluid- saturated rocks when the chemical dissolution system is in a supercritical state?
2 Brief description of φ–p–C approach algorithm
In order to examine the differences between the φ–p–C approach algorithm and the φ–u–C approach algorithm, it is necessary to review the original governing partial differential equations, on which both the algorithms are based. For a two- dimensional chemical dissolution-front instability problem in a fluid-saturated porous rock, the original governing partial differential equations can be described as follows [9, 10]:
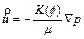 (1)
(1)
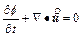 (2)
(2)
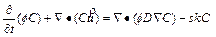 (3)
(3)
 (4)
(4)
where 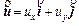 is the Darcy velocity vector within the porous rock; p and C are, respectively, the pore-fluid pressure and the acid/solute concentration (with a unit of moles per pore-fluid volume); μ is the dynamic viscosity of the pore fluid; f is the porosity of the porous rock; D is the diffusivity/ dispersivity of the acid/solute; K(f) is the permeability of the porous rock; χ is the stoichiometric coefficient of the porous rock; k is the rate constant with a unit of m/s; s is the reactive surface area per unit volume of the dissolvable mineral; ρs is the molar density (i.e. moles per volume) of the porous rock.
is the Darcy velocity vector within the porous rock; p and C are, respectively, the pore-fluid pressure and the acid/solute concentration (with a unit of moles per pore-fluid volume); μ is the dynamic viscosity of the pore fluid; f is the porosity of the porous rock; D is the diffusivity/ dispersivity of the acid/solute; K(f) is the permeability of the porous rock; χ is the stoichiometric coefficient of the porous rock; k is the rate constant with a unit of m/s; s is the reactive surface area per unit volume of the dissolvable mineral; ρs is the molar density (i.e. moles per volume) of the porous rock.
It needs to be pointed out that in several situations, such as pore-fluid flow in a horizontal plane or isothermal pore-fluid flow in a vertical plane, gravity effects can be safely omitted in Darcy’s law (i.e. Eq. (1)). Since the isothermal pore-fluid flow is considered in this study, this is the reason why gravity effects were ignored in Eq. (1).
In the φ–p–C approach algorithm, the basic idea is to select the porosity, pore-fluid pressure and acid/solute concentration as three fundamental variables in the governing partial differential equations. This can be done by simply substituting Eq. (1) into Eqs. (2) and (3) to obtain the following equations:
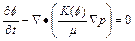 (5)
(5)
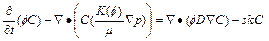 (6)
(6)
Consequently, Eqs. (4) to (6) become the corresponding governing partial differential equations that are considered in the φ–p–C approach algorithm. It should be pointed out that only simple algebraic substitution operations are carried out in the process of deriving these governing partial differential equations for the two-dimensional chemical dissolution-front instability problem in the fluid-saturated porous rock.
Based on the φ–p–C approach algorithm,Eqs. (4) to (6) can be turned into the corresponding dimensionless forms through carrying out a series of algebraic substitution operations. As a result, the finite difference dimensionless equations (with respect to time) for the two-dimensional chemical dissolution-front instability problem in the fluid-saturated porous rock can be expressed as follows:
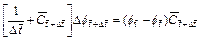 (7)
(7)

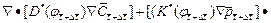
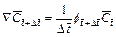 (8)
(8)
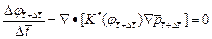 (9)
(9)
where 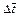 is the dimensionless time-step length;
is the dimensionless time-step length; 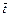 and
and 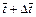 are the dimensionless time at the previous time-step and current time-step respectively;
are the dimensionless time at the previous time-step and current time-step respectively; 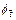 is the porosity at the previous time-step;
is the porosity at the previous time-step; 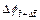 is the porosity increment at the current time-step; f0 is the initial porosity of the porous rock; ff is the final porosity of the porous rock in the completely dissolved region of the dissolvable mineral; γa is the acid dissolution capacity number;
is the porosity increment at the current time-step; f0 is the initial porosity of the porous rock; ff is the final porosity of the porous rock in the completely dissolved region of the dissolvable mineral; γa is the acid dissolution capacity number; 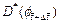 is the dimensionless effective diffusivity/dispersivity of the acid at the current time-step;
is the dimensionless effective diffusivity/dispersivity of the acid at the current time-step;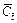 and
and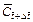 are the dimensionless concentration of the acid at the previous time-step and current time-step respectively;
are the dimensionless concentration of the acid at the previous time-step and current time-step respectively;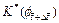 is the dimensionless permeability of the porous rock at the current time-step;
is the dimensionless permeability of the porous rock at the current time-step;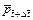 is the dimensionless pore-fluid pressure at the current time-step.
is the dimensionless pore-fluid pressure at the current time-step.
By means of the finite element method, Eqs. (7) to (9) can be converted into the corresponding finite element equations for the chemical dissolution-front instability problem in a fluid-saturated porous rock. After these finite element equations are solved, the computational simulation results can be obtained [8–10].
3 Brief description of φ–u–C approach algorithm
In this section, we consider the same original governing partial-differential equations as those expressed in Eqs. (1) to (4). Since the porosity, velocity of pore-fluid flow and acid/solute concentration are selected as three fundamental variables in the governing partial differential equations, it is necessary to eliminate the pore-fluid pressure from Eq.(2). Mathematically, the following two equations associated with the x-direction and y-direction components of the pore-fluid velocity vector exist through appropriate differential operations:
 (10)
(10)
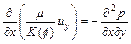 (11)
(11)
where ux and uy are the x-direction and y-direction components of the pore-fluid velocity in the fluid-saturated porous rocks respectively.
If the dynamic viscosity of the pore fluid is treated as a constant, we can eliminate the pore- fluid pressure from Eqs. (10) and (11) to obtain the following equation:
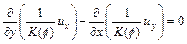 (12)
(12)
Through conducting several mathematical manipulations, Eq. (12) can be rewritten in the following form:
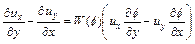 (13)
(13)
where
 (14)
(14)
From the computational point of view, Eq. (13) is ill-posed because it may result in an ill- conditional stiffness matrix in the finite element method. Therefore, it is desirable to improve the computational behavior of this equation through carrying out further differential operations below. Toward this goal, differentiation of both the left-hand side and right-hand side of Eq. (13) with respect to y yields the following equation:

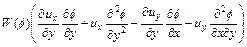 (15)
(15)
Substituting Eq. (15) into Eq. (2) (with appropriate differentiation with respect to x) leads to the following equation:
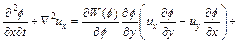
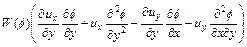 (16)
(16)
Similarly, Eq. (13) can be also rewritten mathematically in the flowing equivalent form:
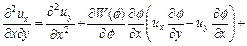
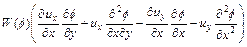 (17)
(17)
Substituting Eq. (17) into Eq. (2) (with appropriate differentiation with respect to y) yields the following equation:
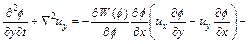
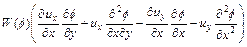 (18)
(18)
Up to now, we have turned Eqs. (2) and (12) into Eqs. (16) and (18), which have much better computational behavior when the finite element method is used. Consequently, in terms of using the φ–u–C approach algorithm, Eqs. (3), (4), (16) and (18) become the governing partial differential equations for the two-dimensional chemical dissolution-front instability problem in a fluid- saturated porous rock.
By following similar procedures as those used in Section 2, we can derive the finite difference dimensionless equations (with respect to time) for Eqs. (3), (4), (16) and (18) as follows:
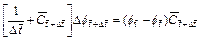 (19)
(19)

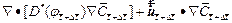
 (20)
(20)
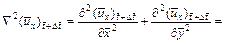
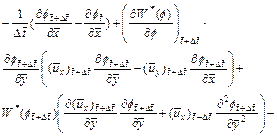
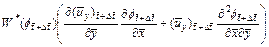 (21)
(21)
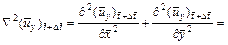
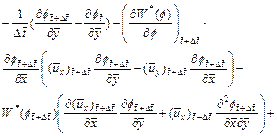
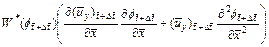 (22)
(22)
where 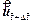 is the dimensionless velocity vector of the pore-fluid flow at the current time-step;
is the dimensionless velocity vector of the pore-fluid flow at the current time-step; 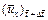 is the x-direction component of the dimensionless velocity vector of the pore-fluid flow at the current time-step;
is the x-direction component of the dimensionless velocity vector of the pore-fluid flow at the current time-step;  is the y-direction component of the dimensionless velocity vector of the pore-fluid flow at the current time-step;
is the y-direction component of the dimensionless velocity vector of the pore-fluid flow at the current time-step; 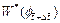 is the dimensionless form of the function (defined in Eq. (14)) at the current time-step;
is the dimensionless form of the function (defined in Eq. (14)) at the current time-step; 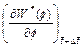 is the first derivative of
is the first derivative of 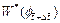 with respect to f at the current time-step. Other quantities have the same meanings as those defined previously.
with respect to f at the current time-step. Other quantities have the same meanings as those defined previously.
Finally, the resulting finite difference dimensionless equations (i.e. Eqs. (19) to (22)) can be also solved through using the finite element method to discretize the spatial domain of the two- dimensional chemical dissolution-front instability problem in a fluid-saturated porous rock [8–10].
4 Computational simulation results using both φ–p–C approach algorithm and φ–u–C approach algorithm
As a typical example of chemical dissolution- front instability problem, an acidization dissolution system, in which carbonate rocks are dissolved by the injected acid, is considered in this section. To investigate the effects of different numerical algorithms on the acidization dissolution-front instability, both the φ–p–C approach algorithm and the φ–u–C approach algorithm are used to simulate the same acidization dissolution system in the fluid-saturated carbonate rock. In order to carry out the forthcoming computational simulations, we need to determine several functions involved in the dimensionless governing equations of the chemical dissolution-front instability problem. The dimensionless effective diffusivity/dispersivity of the acid is assumed as follows:
 (23)
(23)
where ff is the final porosity of the carbonate rock in the completely dissolved region of the dissolvable mineral.
On the other hand, the Kozeny–Carman formula [21] is used to express the porosity– permeability relationship in the computational simulation. This leads to the following two equations:
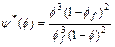 (24)
(24)
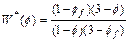 (25)
(25)
Figure 1 shows the computational model for simulating the acidization dissolution-front instability problem in the fluid-saturated carbonate rock. In this figure, the dimensionless width (i.e. 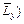 and dimensionless length (i.e.
and dimensionless length (i.e.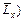 of the computational domain are equal to 100 and 200 respectively. This computational domain is discretized into 19701 four-node square elements with 20000 nodal points in total. Both the top and the bottom boundaries of the computational domain are assumed to be impermeable for both the acid concentration and the pore-fluid flow. If the acid is injected from the far field (that is out of the computational domain), a time-dependent dimensionless acid concentration boundary condition (i.e.
of the computational domain are equal to 100 and 200 respectively. This computational domain is discretized into 19701 four-node square elements with 20000 nodal points in total. Both the top and the bottom boundaries of the computational domain are assumed to be impermeable for both the acid concentration and the pore-fluid flow. If the acid is injected from the far field (that is out of the computational domain), a time-dependent dimensionless acid concentration boundary condition (i.e. 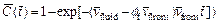 needs to be applied on the left boundary of the computational domain, where
needs to be applied on the left boundary of the computational domain, where 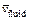 is the dimensionless velocity of the injected pore-fluid flow (in the x direction) and
is the dimensionless velocity of the injected pore-fluid flow (in the x direction) and 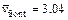 is the dimensionless propagation speed of the acidization dissolution front when the acidization dissolution system is in a subcritical state [9, 10]. The initial porosity is equal to 0.1 (i.e. f0=0.1) and the initial dimensionless acid concentration is equal to zero (
is the dimensionless propagation speed of the acidization dissolution front when the acidization dissolution system is in a subcritical state [9, 10]. The initial porosity is equal to 0.1 (i.e. f0=0.1) and the initial dimensionless acid concentration is equal to zero ( ) in the computational domain. The final porosity (i.e. ff), which is equal to 0.2, is applied on the left boundary of the computational domain. Since the rock deformation is usually ignored in the chemical dissolution-front instability problem, the stress state of the fluid-saturated carbonate rock is not required in the computational model.
) in the computational domain. The final porosity (i.e. ff), which is equal to 0.2, is applied on the left boundary of the computational domain. Since the rock deformation is usually ignored in the chemical dissolution-front instability problem, the stress state of the fluid-saturated carbonate rock is not required in the computational model.

Figure 1 Geometry and boundary conditions of acidization dissolution problem in a fluid-saturated carbonate rock
In the case of using the φ–p–C approach algorithm, 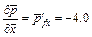 is applied on the left boundary of the computational domain, while in the case of using the φ–u–C approach algorithm,
is applied on the left boundary of the computational domain, while in the case of using the φ–u–C approach algorithm,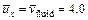 is applied on the left boundary of the computational domain. This means that the Zhao number of the acidization dissolution system is equal to 4.0 in the computational model. The acid dissolution capacity number is equal to 0.76, while the dimensionless time-step length is equal to 0.2 for all the forthcoming computational simulations. A small perturbation of 20% of the initial porosity (i.e. f0=0.1) is applied to the initial porosity field before running the computational model. The initial condition of the dimensionless acid concentration is equal to zero in the whole computational domain. In addition, a dimensionless pore-fluid pressure (i.e.
is applied on the left boundary of the computational domain. This means that the Zhao number of the acidization dissolution system is equal to 4.0 in the computational model. The acid dissolution capacity number is equal to 0.76, while the dimensionless time-step length is equal to 0.2 for all the forthcoming computational simulations. A small perturbation of 20% of the initial porosity (i.e. f0=0.1) is applied to the initial porosity field before running the computational model. The initial condition of the dimensionless acid concentration is equal to zero in the whole computational domain. In addition, a dimensionless pore-fluid pressure (i.e.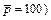 is applied on the right boundary of the computational domain.
is applied on the right boundary of the computational domain.
Figure 2 shows the simulation results of the acidization dissolution-front propagation in the fluid-saturated carbonate rock in the case of using the φ–p–C approach algorithm, while Figure 3 shows the simulation results of the acidization dissolution-front propagation in the fluid-saturated carbonate rock in the case of using the φ–u–C approach algorithm. Note that the porosity front is commonly used to represent the acidization dissolution front in the fluid-saturated carbonate rock. From the computational simulation results (shown in Figure 2), it is clearly observed that in the case of using the φ–p–C approach algorithm, the acidization dissolution front gradually evolves from a planar shape (at the early stage of the computational simulation) into a finger-like shape (at the later stage of the computational simulation). This phenomenon agrees very well with the theoretical expectation. From the theoretical analysis in the previous study [9, 10], the critical Zhao number (associated with the fundamental mode) of this acidization dissolution system is equal to 1.77. Since the Zhao number of the acidization dissolution system is equal to 4.0, which is greater than the corresponding critical Zhao number, the acidization dissolution front is unstable when it propagates in the acidization dissolution system, so that it can evolve from a simple shape at the early stage of the computational simulation into a complicated shape at the later stage of the computational simulation.

Figure 2 Simulation results of acidization dissolution-front propagation in fluid-saturated carbonate rock by using φ–p–C approach algorithm (Porosity):

Figure 3 Simulation results of acidization dissolution-front propagation in fluid-saturated carbonate rock by using the φ–u–C approach algorithm (Porosity):
However, from the computational simulation results (shown in Figure 3), it can be observed that in the case of using the φ–u–C approach algorithm, the acidization dissolution front almost does not change its shape during its propagation in the computational simulation model. This means that the computational simulation results obtained from using the φ–u–C approach algorithm are totally different, not only from those obtained from using the φ–p–C approach algorithm, but also from the theoretical expectation. The main reason to cause such a difference is that in the process of deriving the φ–u–C approach algorithm, several differential operations were used to improve the convergence behavior of the φ–u–C approach algorithm. Since each differential operation may enable the stiffness matrix of the acidization dissolution system to become stiffer, the corresponding acidization dissolution system, which is represented by the stiffer stiffness matrix, becomes more stable. This indicates that the use of the φ–u–C approach algorithm can stabilize the acidization dissolution system, so that it is difficult for the acidization dissolution front to evolve from a simple shape at the early stage of the computational simulation into a complicated shape at the later stage of the computational simulation. Therefore, it may be concluded that the φ–u–C approach algorithm is not suitable for dealing with the chemical dissolution-front propagation problem in supercritical chemical dissolution systems.
Figure 4 shows the simulated streamline results for the acidization dissolution-front propagation problem in the fluid-saturated carbonate rock in the case of using the φ–p–C approach algorithm, while Figure 5 shows the simulated streamline results for the same acidization dissolution-front propagation problem in the case of using the φ–u–C approach algorithm. Since the finger-like dissolution front can provide preferential flow channels in the fluid-saturated carbonate rock, there are several flow-focusing zones, which are characterized by the denser distribution of streamlines in the computational model. This phenomenon can be clearly observed from the computational simulation results obtained in the case of using the φ–p–C approach algorithm, especially at the later stage of the computational simulation. However, such a phenomenon does not exist in the computational simulation results when they are obtained in the case of using the φ–u–C approach algorithm. This further demonstrates that the φ–u–C approach algorithm is not suitable for dealing with the chemical dissolution-front propagation problem in supercritical chemical dissolution systems.
It is noted that although only one typical example is used to demonstrate the weakness of using the φ–u–C approach algorithm for dealing with the chemical dissolution-front propagation problem in supercritical chemical dissolution systems, the previous and existing theoretical study [10] can also support the conclusion drawn from using this typical example.
5 Conclusions
In order to investigate the effects of different numerical algorithms on the computational simulation of chemical dissolution-front instability problems in fluid-saturated porous rocks, both the φ–p–C approach algorithm and the φ–u–C approach algorithm have been employed, in this paper, to simulate the acidization dissolution-front propagation in fluid-saturated carbonate rocks when the acidization dissolution system is in a supercritical state. The related computational simulation results have demonstrated that: 1) the φ–p–C approach algorithm can realistically simulate the evolution processes of unstable chemical dissolution-front propagation in supercritical chemical dissolution systems. 2) The φ–u–C approach algorithm fails to simulate the evolution processes of unstable chemical dissolution-front propagation in supercritical chemical dissolution systems. 3) The extra differential operation is the main source to result in the failure of the φ–u–C approach algorithm. Therefore, precaution should be taken when we select the numerical algorithms for dealing with chemical dissolution-front instability problems in fluid-saturated porous rocks, especially for supercritical chemical dissolution systems.

Figure 4 Simulation results of acidization dissolution-front propagation in fluid-saturated carbonate rock by using φ–p–C approach algorithm (Streamline):

Figure 5 Simulation results of acidization dissolution-front propagation in fluid-saturated carbonate rock by using φ–u–C approach algorithm (Streamline):
References
[1] CHADAM J, HOFF D, MERINO E, ORTOLEVA P, SEN A. Reactive infiltration instabilities [J]. IMA Journal of Applied Mathematics, 1986, 36: 207–221.
[2] CHADAM J, ORTOLEVA P, SEN A. A weekly nonlinear stability analysis of the reactive infiltration interface [J]. IMA Journal of Applied Mathematics, 1988, 48: 1362–1378.
[3] ORMOND A, ORTOLEVA P. Numerical modeling of reaction-induced cavities in a porous rock [J]. Journal of Geophysical Research, 2000, 105: 16737–16747.
[4] ORTOLEVA P, CHADAM J, MERINO E, SEN A. Geochemical self-organization II: The reactive-infiltration instability [J]. American Journal of Science, 1987, 287: 1008–1040.
[5] CHEN J S, LIU C W. Numerical simulation of the evolution of aquifer porosity and species concentrations during reactive transport [J]. Computers and Geosciences, 2002, 28: 485–499.
[6] CHEN J S, LIU C W, LAI G X, NI C F. Effects of mechanical dispersion on the morphological evolution of a chemical dissolution front in a fluid-saturated porous medium [J]. Journal of Hydrology, 2009, 373: 96–102.
[7] LAI K H, CHEN J S, LIU C W, YANG S H. Effect of permeability-porosity functions on simulated morphological evolution of a chemical dissolution front in a fluid-saturated porous medium [J]. Hydrological Processes, 2014, 28: 16–24.
[8] ZHAO C, HOBBS B E, HORNBY P, ORD A, PENG S, LIU L. Theoretical and numerical analyses of chemical- dissolution front instability in fluid-saturated porous rocks [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 32: 1107–1130.
[9] ZHAO C. Physical and chemical dissolution front instability in porous media: theoretical analyses and computational simulations [M]. Berlin: Springer, 2014: 354.
[10] ZHAO C, HOBBS B E, ORD A. A new alternative approach for investigating acidization dissolution front propagation in fluid-saturated rocks [J]. Science China: Technological Sciences, 2017, 60: 1197–1210.
[11] ZHAO C, SCHAUBS P, HOBBS B E. Effects of porosity heterogeneity on chemical dissolution-front instability in fluid-saturated rocks [J]. Journal of Central South University, 2017, 24: 720–725.
[12] COHEN C E, DING D, QUINTARD M, BAZIN B. From pore scale to wellbore scale: impact of geometry on wormhole growth in carbonate acidization [J]. Chemical Engineering Science, 2008, 63: 3088–3099.
[13] GOLFIER F, ZARCONE C, BAZIN B, LENORMAND R, LASSEUX D, QUINTARD M. On the ability of a Darcy-scale model to capture wormhole formation during the dissolution of a porous medium [J]. Journal of Fluid Mechanics, 2002, 457: 213–254.
[14] HINCH E J, BHATT B S. Stability of an acid front moving through porous rock [J]. Journal of Fluid Mechanics, 1990, 212: 279–288.
[15] KALIA N, BALAKOTAIAH V. Modeling and analysis of wormhole formation in reactive dissolution in carbonate rocks [J]. Chemical Engineering Science, 2007, 62: 919–928.
[16] KALIA N, BALAKOTAIAH V. Effect of medium heterogeneities on reactive dissolution of carbonates [J]. Chemical Engineering Science, 2009, 64: 376–390.
[17] SHERWOOD J D. Stability of a plane reaction front in a porous medium [J]. Chemical Engineering Science, 1987, 42: 1823–1829.
[18] GUNTER W D, PERKINS E H, MCCANN T J. Aquifer disposal of CO2-rich gases: Reaction design for added capacity [J]. Energy Conversion and Management, 1993, 34: 941–948.
[19] BACHU S, SHAW J. Evaluation of the CO2 sequestration capacity in Alberta’s oil and gas reservoirs at depletion and the effect of underlying aquifers [J]. Petroleum Technology, 2003, 42: 51–61.
[20] DALKHAA C, SHEVALIER M, NIGHTINGALE M, MAYER B. 2-D reactive transport modeling of the fate of CO2 injected into a saline aquifer in the Wabamun Lake Area, Alberta, Canada [J]. Applied Geochemistry, 2013, 38: 10–23.
[21] BEAR J. Dynamics of fluids in porous media [M]. Amsterdam: Elsevier, 1972: 636.
(Edited by YANG Hua)
中文导读
不同数值算法对模拟饱水孔隙岩石中化学溶解面非稳定性的影响
摘要:鉴于求得解析解的困难,需要采用数值方法和算法得到大量科学和工程问题的计算模拟结果。这对求解饱水孔隙岩石中化学溶解面非稳定性问题而言也不例外。由于这类非稳定性问题可具有常规解和非常规解,很有必要探讨不同数值算法对模拟饱水孔隙岩石中化学溶解面非稳定性的影响。因此,本文考虑了与常用有限元相关的2种不同数值算法。在第1种数值算法中,孔隙率、孔隙流体压力和酸液浓度被选为基本变量。在第2种数值算法中,孔隙率、孔隙流体流速和酸液浓度被选为基本变量。相关的计算模拟结果表明:(1) 第1种数值算法可真实地模拟非稳定化学溶解面在化学溶解系统中传播时的演化过程;(2) 第2种数值算法不能模拟非稳定化学溶解面在化学溶解系统中传播时的演化过程;(3) 过度的数学微分运算是导致第2种数值算法失效的主要原因。
关键词:数值算法;化学溶解;溶解面非稳定性;计算模拟;孔隙岩石
Foundation item: Project(11272359) supported by the National Natural Science Foundation of China
Received date: 2017-03-27; Accepted date: 2017-09-24
Corresponding author: ZHAO Chong-bin, Professor; Tel: +86–731–88830028; E-mail: chongbin.zhao@iinet.net.au; ORCID: 0000- 0001-7093-2282

