J. Cent. South Univ. (2019) 26: 2418-2431

DOI: https://doi.org/10.1007/s11771-019-4184-6

Demodulation spectrum analysis for multi-fault diagnosis of rolling bearing via chirplet path pursuit

LIU Dong-dong(刘东东), CHENG Wei-dong(程卫东), WEN Wei-gang(温伟刚)

School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University,Beijing 100004, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: The vibration signals of multi-fault rolling bearings under nonstationary conditions are characterized by intricate modulation features, making it difficult to identify the fault characteristic frequency. To remove the time-varying behavior caused by speed fluctuation, the phase function of target component is necessary. However, the frequency components induced by different faults interfere with each other. More importantly, the complex sideband clusters around the characteristic frequency further hinder the spectrum interpretation. As such, we propose a demodulation spectrum analysis method for multi-fault bearing detection via chirplet path pursuit. First, the envelope signal is obtained by applying Hilbert transform to the raw signal. Second, the characteristic frequency is extracted via chirplet path pursuit, and the other underlying components are calculated by the characteristic coefficient. Then, the energy factors of all components are determined according to the time-varying behavior of instantaneous frequency. Next, the final demodulated signal is obtained by iteratively applying generalized demodulation with tunable E-factor and then the band pass filter is designed to separate the demodulated component. Finally, the fault pattern can be identified by matching the prominent peaks in the demodulation spectrum with the theoretical characteristic frequencies. The method is validated by simulated and experimental signals.

Key words: rolling bearing; demodulation spectrum; multi-fault detection; nonstationary; chirplet path pursuit

Cite this article as: LIU Dong-dong, CHENG Wei-dong, WEN Wei-gang. Demodulation spectrum analysis for multi-fault diagnosis of rolling bearing via chirplet path pursuit [J]. Journal of Central South University, 2019, 26(9): 2418-2431. DOI: https://doi.org/10.1007/s11771-019-4184-6.

1 Introduction

Rolling bearings are widely used in the rotating machinery for their unique advantages of high bearing capacity and low friction coefficient. However, they are particularly vulnerable to fault, because of the rough and long-term working conditions. The faults in bearing may cause serious damage to the entire mechanical system. Therefore, it is of great significance to detect the bearing fault to avoid costly breakdown. To pinpoint the fault pattern, many effective methods, such as envelope analysis [1, 2], time-frequency spectrum [3, 4], ensemble empirical mode decomposition [5], and spectral kurtosis analysis [6, 7], are developed. However, the overwhelming majority are proposed to reveal the mono-fault characteristic. Because of the intricate modulation features and the nonstationary operating conditions, the fault diagnosis of multi-fault bearings is still a challenge.

To date, some multi-fault detection methods have been developed. YU et al [8] proposed morphological component analysis to detect the gear and bearing faults in gearboxes. PURUSHOTHAM et al [9] utilized discrete wavelet transform to effectively detect multiple faults in ball bearing. TENG et al [10] identified the weak bearing features contaminated by intensive noise via complex wavelet transform. CHEN et al [11] employed multi-kemel support vector machine to diagnose complex fault in roller bearing. HE et al [12] developed optimization criteria for adaptive redundant multiwavelet packet to reveal compound faults in gearbox. JIANG et al [13] applied the multiwavelet packet to improve the ensemble empirical mode decomposition for multi-fault diagnosis of rotating machinery. LI et al [14] developed the wavelet autoregressive and principal component analysis for gear multi-fault diagnosis. In addition to the detection methods, dynamic models [15, 16] have been derived to provide a theoretical guide for multi-fault detection. These contributions have enriched the literature for multi- fault detection. Nevertheless, the effectiveness of most methods is depended on the stationary assumption.

Bearing vibration signals, under time-varying rotating speed, feature more complex amplitude modulation and frequency modulation characteristics, thus making it difficult to identify the faults based on the conventional Fourier representation. Order tracking [17-22] is one of the most effective tools to eliminate the influence of speed fluctuation. YANG et al [18] utilized order tracking and local mean decomposition to extract bearing fault features under variable speed condition. LI et al [19] employed sparse decomposition and order tracking to detect gearbox fault under nonstationary condition. To avoid the installation of equipment, the instantaneous frequency estimation technique is proposed. ZHAO et al [20] proposed a chirplet based method to extract a certain harmonic of rotating frequency. WANG et al [21] extracted the bearing characteristic frequency from the time-frequency representation for demodulating and resampling the bearing signal. ZHAO et al [22] employed empirical mode decomposition soft-thresholding denoising method to filter the bearing signal and then extracted the instantaneous frequency from the envelope time-frequency representation. SHI et al [23] adopted windowed fractal dimension and time-frequency method to extracted bearing fault characteristic frequency. However, order tracking entails low computational efficiency [24] and envelope deformation [25]. The instantaneous frequency estimation technique based on phase demodulation [26, 27] is subjected to the constraint of limited speed fluctuation. Another time- frequency representation based approach [28] is limited by the time-frequency resolution.

Due to the modulation features of bearing signals, the rotating frequency does exist in the envelope signal. However, the magnitude is so low, even overwhelmed by interference noise, that cannot be estimated directly in the vibration signal [29]. High resolution time-frequency methods, jointing the peak search method, can also be employed to extract the instantaneous frequency. However, for multi-fault bearing signals, the characteristic frequency components induced by different parts of rolling bearing interfere with each other. The trajectories of different frequency components on the time-frequency plane are very close to each other, which hinders the effective detection of the characteristic frequency. Therefore, the commonly used methods cannot be used to detect a continuous instantaneous frequency from the vibration signal of multi-fault rolling bearing. Through our extensive literature search, no research has been reported on the multi-fault bearing detection under nonstationary conditions without the measured rotating speed information severed as a reference.

Recently, CANDES et al [30] proposed chirplet path pursuit to detect the nonstationary behaviors of highly noisy oscillatory signal. The method is implemented by chaining a series of chirplets together to approximate the instantaneous frequency. Compared to peak search method, chirplet path pursuit is more robust than noise. More importantly, according to the connecting principle, the frequency offset and slope at the junctures of adjacent chirplets in the selected group are small. Therefore, the instantaneous frequency extracted by chirplet path pursuit is continuous and free from frequency mutation. Considering the nonstationary features and the interactions of different frequency components, the unique property of chirplet path pursuit is fully exploited in approximating the characteristic frequency of multi-fault bearing signals under nonstationary conditions.

Based on the detected characteristic frequency, it is necessary to restore the periodicity of the signal to meet the requirement of Fourier transform. Due to the convolution property of Fourier transform, bearing signals exhibit complex sideband spectrum structures, which hinder the effective identification of characteristic frequency. To improve the time- frequency representation, generalized demodulation (GD) [31] is proposed, which can convert the curvilinear instantaneous frequency to constant frequency for wavelet transform. Inspired by the merits of GD, it is further adopted for frequency representation. However, the demodulation precision is far from satisfactory. According to the time-varying behavior of bearing signals, the accuracy can be enhanced by changing the energy concentration location. Therefore, generalized demodulation with tunable energy factor (E-factor) (GDTEF) approach is developed [32], which is more robust to the running condition and background noise. The idea is to convert the energy of nonstationary frequency component to the corresponding E-factor, where the precision is relatively higher.

Motivated by the above considerations, the enhanced demodulation spectrum analysis for multi-fault detection of rolling bearing via chirplet path pursuit is proposed. First, the envelope signal is obtained by applying Hilbert transform to the raw signal. Second, the characteristic frequency is extracted via chirplet path pursuit, and the other underlying components are calculated by the characteristic coefficient. Then, the E-factors of all components are determined according to the time-varying behavior of instantaneous frequency. Next, the final demodulated signal is obtained by iteratively applying GDTEF to the signal and then the band pass filter is designed to separate the demodulated component. Finally, the fault pattern can be identified by matching the prominent peaks in the demodulation spectrum with the theoretical characteristic frequencies.

Hereafter, this paper is organized as follows. In Section 2, we propose the demodulation spectrum analysis for multi-fault bearing detection via chirplet path pursuit. In Section 3, the proposed demodulation spectrum analysis is illustrated by the numerical simulated bearing signals. In Section 4, the method is further validated by the experimental signal. The conclusions are drawn in Section 5.

2 Proposed rolling bearing multi-fault detection method

To identify the bearing fault feature, it is necessary to comprehend the constituent frequency components and their variation characteristics of bearing signals under nonstationary conditions. When a rolling bearing has a fault, the fault point will strike its matching rolling element, resulting in a series of impulses. These impulses contain abundant fault information, including the fault location and the rotating frequency. Therefore, the repetition frequency of the impulses is called fault characteristic frequency. For a specific rolling bearing, the value of fault characteristic frequency can be derived by geometric parameters of the bearing and the rotating frequency.

Identifying the characteristic frequencies, including the fault characteristic frequency, the modulation rotating frequency and their harmonics, can reveal the fault signature. However, under nonstationary conditions, these components exhibit a time-varying behavior, which complicates the effective identification to a certain extent. Due to the modulation features, there are complex sideband clusters around resonance frequency in the Fourier spectrum as well as the time-frequency spectrum (illustrated in Figure 1(a)), thus making the representations of raw signal, especially the multi-fault bearing signal, cannot reveal the fault signature.

Amplitude demodulation is the most commonly used method to avoid the intricate sidebands. However, the envelope frequency spectrum or time-frequency representation (illustrated in Figure 1(b)) still involves some sidebands around fault characteristic frequency. More importantly, when the rotating speed fluctuates, the energy of the fault characteristic frequency (F_fc) no longer concentrates in a constant frequency value, but distributes in a certain range (Cf_rmin≤F_fc≤Cf_rmax, where C is the fault characteristic coefficient, determined by bearing geometric parameter and the defect location, f_rmin and f_rmax represent the minimum and the maximum rotating frequencies respectively), which hinders the effective identification of fault pattern.

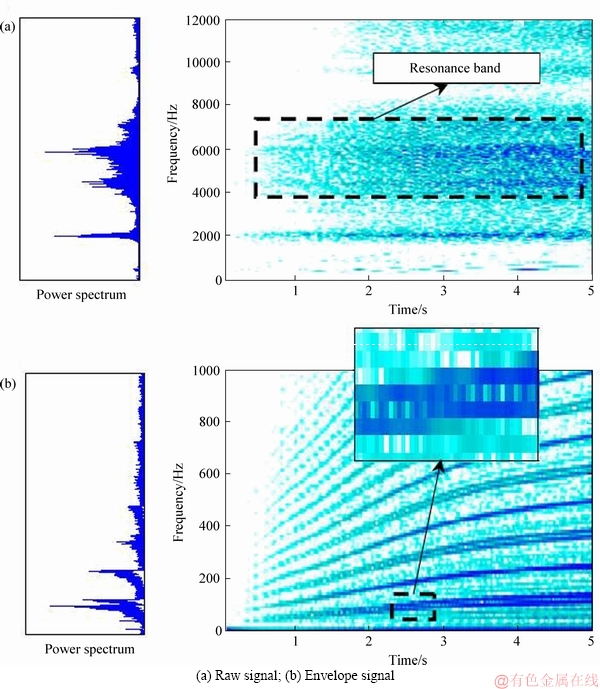
Figure 1 Time-frequency spectra:

2.1 Chirplet path pursuit

To pinpoint the characteristic frequency components in a faithful frequency representation of the nonstationary signal, it is highly necessary to extract the instantaneous frequency for estimating the corresponding phase. Chirplet path pursuit [30] is a quite effective approach to identifying the instantaneous frequency of nonstationary signal. The algorithm is implemented by connecting a series of chirplet atoms whose instantaneous frequencies are linear with time to approximate the instantaneous frequency of the nonstationary signal.

For a signal 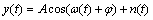(where A demotes the amplitude, ω(t) is the instantaneous phase, φ is the initial phase, n(t) is the noise), if φ(t) is a continuous and derivable function, the instantaneous frequency of y(t) can be approximated by connecting a series of atoms with the instantaneous frequency linear to time. These chirplet atoms are selected from a chirplet dictionary defined by

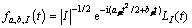             (1)

where I denotes the dyadic interval, I=[kT2^-j, (k+1)T2^-j], j is the scale coefficient, 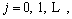log₂N-1; T is the sample time, 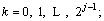a_u and b_u are the slope and offset parameters, which are determined by the scale j and the prior information of target object. The value of a_ut+b_u must be less than f_s/2 (f_s is the sampling frequency) to satisfy the sampling theorem. L_I(t) is a rectangular window function, if 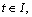L_I(t)=1, if 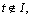L_I(t)=0. I ^-1/2 is a normalization factor, leading to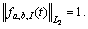

According to the phase of chirplet atom a_ut²+b_ut, the instantaneous frequency of a chirplet is linear to time and equals a_ut+b_u. The principle of chirplet path pursuit is to find a best way to link the chirplet atoms to approximate the instantaneous frequency of y(t).

In the dyadic interval, the atom group of selecting to link should be most relevant to the signal y(t) to best approximate the instantaneous frequency of y(t). That means that the atoms, in the dyadic interval I, should have the maximum correlation coefficient β_I.

                   (2)

where <·> demotes the inner product operator. The corresponding component d_I(t) of the maximum coefficient β_I can be calculated as:

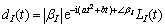                 (3)

The procedure of the algorithm can be summarized as follows.

1) Determine the atom group most relevant to the signal y(t) in the dyadic interval I, and then approximate the component by the corresponding signal d_I(t) of the maximum correlation coefficient.

2) Construct the signal d_I(t) with the same time span and the largest energy among all the possible paths based on the best path method.

Given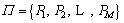is a set containing all the elements to form the possible paths to construct the signal, the path 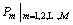must cover the time span L with no overlap. The energy of signal x(t) can be calculated by

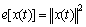                           (4)

To approximate the signal y(t), the constructing signal d(t) should satisfy

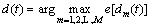                  (5)

Based on the above illustration, it can be observed that the chirplet path pursuit is implemented by connecting a selected group of chirplet atoms to approximate the instantaneous frequency of the nonstationary signal. According to the best path connecting method, the frequency offset and slope at the junctures of adjacent chirplets in the selected group are small. Therefore, the extracted frequency is continuous and free from frequency mutation. In the multi-fault bearing vibration, the characteristic frequencies induced by different faults interfere with each other. To address this issue, the merit of chirplet path pursuit is fully exploited in extracting the instantaneous characteristic frequency from the bearing vibration signal to estimate the relevant phase.

2.2 Generalized demodulation with tunable E-factor

Generalized demodulation [31] can be employed to demodulate the nonstationary signal identifying the frequency content. However, the method is sensitive to the phase of target frequency especially the initial frequency. To overcome the unsatisfied demodulation precision, the GDTEF [32] is proposed.

For a signal x(t), f(t) is the instantaneous frequency of x(t), according the time-varing behavior of f(t), the E-factor is set to f_e(f_min(t)≤f_e≤f_max(t)), where t_e is the time of f_e. The signal x(t) is constructed by E-factor as:

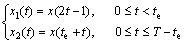              (6)

where T is the sampling time. The instantaneous frequencies of x₁(t) and x₂(t) are calculated f₁(t) and f₂(t) respectively based on the frequency f(t) and E-factor f_e.

The generalized Fourier transform of x₁(t) is defined as S_1G(f):

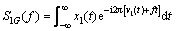               (7)

Correspondingly, the inverse generalized Fourier transform can be obtained as:

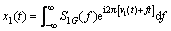
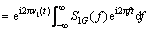               (8)

If the generalized Fourier transform 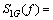, then 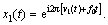This means that the energy of x₁(t) will be concentrated to a constant f₀ by operating the appropriate generalized Fourier transform.

If the calculated instantaneous frequency of x₁(t) is 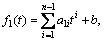then f_e is assigned to b approximately according to the time-varying behavior of the signal 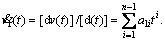The phase of the generalized transform of x₁(t) can be obtained by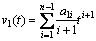via integrating 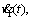where a_1i (i=1, 2, …, n) denotes the polynomial coefficient calculated by f₁(t)=f(2t-1) (0≤te).

Then the demodulated signal 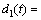is obtained by demodulating x₁(t) based on v₁(t).

According to the instantaneous frequency of the signal x₂(t), the demodulated signal of x₂(t) can be derived by the same approach, then .

Finally, the demodulated signal of x(t) can be determined by d₁(t) and d₂(t) as:

               (9)

2.3 Rolling bearing multi-fault detection via proposed method

The vibration signals of multi-fault bearing consist of several nonstationary components whose time-varying behavior and interactive modulation reflect the running condition. Efficient and robust detection method will help us better describe the underlying bearing state. In order to estimate the phase of the target component for demodulation, chirplet path pursuit is applied to the envelope due to its unique merits in detecting nonstationary signals. The method avoids the interference of the characteristic frequencies induced by different fault points, extracting a continuous yet accurate instantaneous frequency.

Based on the estimated phase, we further exploit the properties of GDTEF in converting the energy of relevant characteristic frequencies, i.e., outer race fault characteristic frequency, inner race fault characteristic frequency, modulation rotating frequency, as well as their harmonics, to their corresponding E-factors for satisfying the requirement of Fourier transform. However, in terms of the multi-fault bearing signal, iterating each demodulated component is subjected to interference components as well as the accumulated noise. To better describe the characteristic frequency content, the band pass filter around the center frequency E-factor is designed to separate each demodulated component.

In general, the larger the magnitude of one instantaneous frequency is, the higher the estimating precision via chirplet path pursuit will be. Therefore, the E-factor is automatically set to the maximum frequency value of the target component. The procedure is detailed as below:

1) Apply Hilbert transform to the raw signal to obtain the envelope signal for demodulation.

2) Extract the fault characteristic frequency via chirplet path pursuit, and then calculate the other components via the characteristic coefficient.

3) Determine the E-factors of all characteristic frequency components according to the time- varying behavior of the vibration signal.

4) Obtain the final demodulated signal by iteratively applying GDTEF to the envelope signal and then design the band pass filter with the central frequency of E-factor to separate the demodulated component.

5) Identify the fault pattern by matching the dominant peaks in the demodulated spectrum with the theoretical characteristic frequencies of the bearing.

3 Simulation evaluation

In this section, the numerically simulated bearing vibration signals are analyzed to illustrate the effectiveness of the proposed method. To fully describe the modulation feature, the amplitude modulation by shaft rotating speed is added to the simulated model of rolling bearing in Ref. [28].

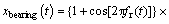
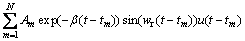 (10)

where f_r(t) is the bearing rotating speed; N is the impulses number induced by bearing defect; A_m is the magnitude of the mth impulse; β is damping characteristic; u(t) is a unit step function; w_r is high resonance frequency of the mechanical part excited by bearing fault; t_m is occurrence time of the mth impulse.

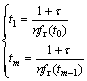, m=2, 3, …, N              (11)

where τ is the slippage coefficient of rolling elements, which varies from 0.01 to 0.02 and n is the number of impulse per rotation.

The simulated model of multi-fault bearing is constructed as:

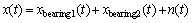            (12)

where 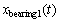denotes the vibration induced by one bearing defect; 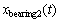is the waveform generated by the other defect; n(t) is the Gaussian noise to mimic the background noise interference. The detailed parameters are listed in Table 1.

Table 1 Parameters of simulated signal

The rotating frequency is set to f_r(t)= -15(t-1.9)²+60 to mimic a time-variant running condition. The minimum and the maximum rotating frequencies are 5.85 Hz at t=0 s and 60 Hz at t=1.9 s respectively. To research the interference of different defects rather than the noise, the Gaussian noise is firstly added to the model with a relatively high signal-to-noise ratio (SNR) of 10 dB.Figure 2(a) shows the waveform of the simulated vibration. From this figure, it can be observed that the change rule of the amplitude is roughly consistent with the trend of rotating frequency. Figure 2(b) shows the frequency spectrum of the raw signal. The energy of the simulated signal is mainly distributed in vicinity of the resonance frequency. Figure 2(c) shows the time-frequency spectrum of the envelope. Figure 2(d) shows the instantaneous fault characteristic frequency (IFCF) extracted by applying peak search to the time-frequency representation. Although a frequency trend relevent to the rotational speed is revealed, the trend is interfered by the adjacent charactristic frequency components. Hence, the interference of characristic frequencies induced by different faults hunders the detection of instantaneous frequency using peak search method. Figure 2(e) shows the envelope signal. The IFCF trend estimated by applying chirplet path pursuit to the envelope is shown in Figure 2(f). The trend is consistent with the outer race fault characterist frequency with a high accurancy.

Figure 2(g) shows the demodulation spectrum by iteratively applying GD to the signal guided by chirplet path pursuit, in which although some peaks appear, their locations are far from the theoretical characteristic frequencies (where the corresponding theoretical values of relevant components are marked by dotted lines with different colors to distinguish the diverse components). Figure 2(h) shows the demodulation spectrum via the proposed method, in which some prominent peaks appear at the locations associated with outer race fault characteristic frequency F_fc0, inner race fault characteristic frequency F_fci, rotational speed f_r, as well as their harmonics. This proves that the proposed method can pinpoint the fault characteristic frequencies of multi-fault bearing with the chirplet path pursuit served as a basis, and then identify the fault pattern.

To evaluate the anti-noise ability of the method, the simulated signals under different SNR values are constructed. The demodulated spectra under the SNR of 0 dB, -5 dB and -10 dB are shown in Figure 3. In the demodulated spectra via the proposed method, some prominent peaks are revealed at outer race fault characteristic frequency F_fc0, inner race fault characteristic frequency F_fci, rotating frequency f_r, as well as their harmonics. Although the amplitudes of demodulated frequencies under different noise levels vary slightly, the demodulation precisions have nearly unchanged. However, though some peaks appear in the spectra via the traditional method, these peaks deviate from the theoretical frequencies and are surrounded or even overwhelmed by the interfering noise. This confirms the noise robustness of the proposed method.

4 Experimental evaluation

In this section, the effectiveness of the proposed method is validated using the experimental signal measured by a vibration test rig. The experimental setup and the tested bearing are shown in Figure 4. The vibration signals are collected by an accelerometer mounted on the top of bearing support casing extremely close to the bearing. The sampling rate is set to 24000 Hz.An encoder is mounted at the drive end to measure the corresponding rotating speed. To mimic the bearing faults, the manually cutting defects are introduced to the inner and outer races of the tested bearing. The rotating frequency increases from 13.1 to 56.2 Hz with an approximate parabola pattern. The data is collected for 5 s. The detailed parameters of the tested bearing are listed in Table 2.

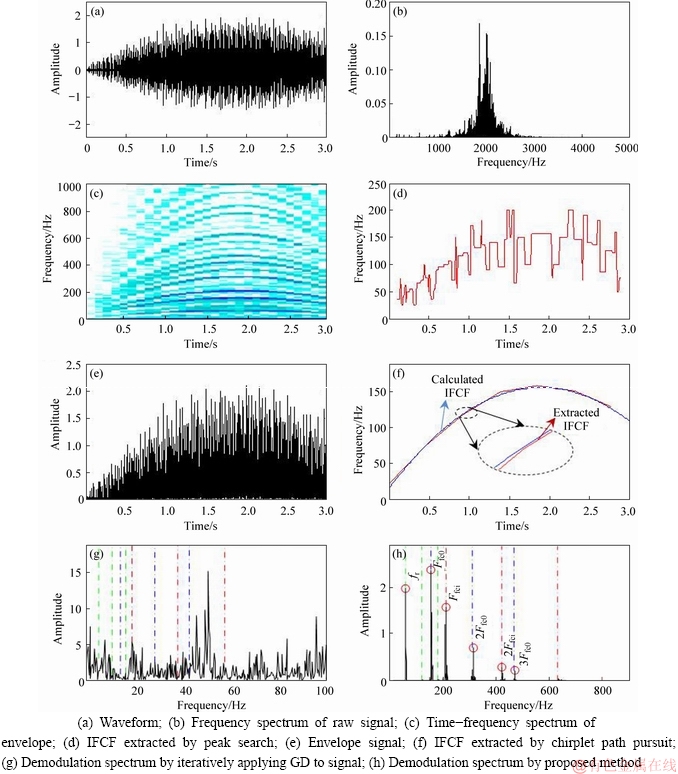
Figure 2 Simulated case:

Figures 5(a) and (b) show the waveform and its corresponding shaft rotating speed. Figure 5(c) shows the envelope time-frequency representation obtained by applying short time Fourier transform to the envelope. In the spectrum, although clear trends approximately proportional to the rotating frequency are revealed, they cannot provide sufficient evidence of bearing fault, not to mention the multi-fault. The rotor unbalance or manufacturing error may produce such modulation frequency components. The IFCF extracted by applying chirplet path pursuit to the envelope (illustrated in Figure 5(d)) is shown in Figure 5(e). It can be observed that the change trend is approximately consistent with the IFCF calculated by measured rotating frequency.

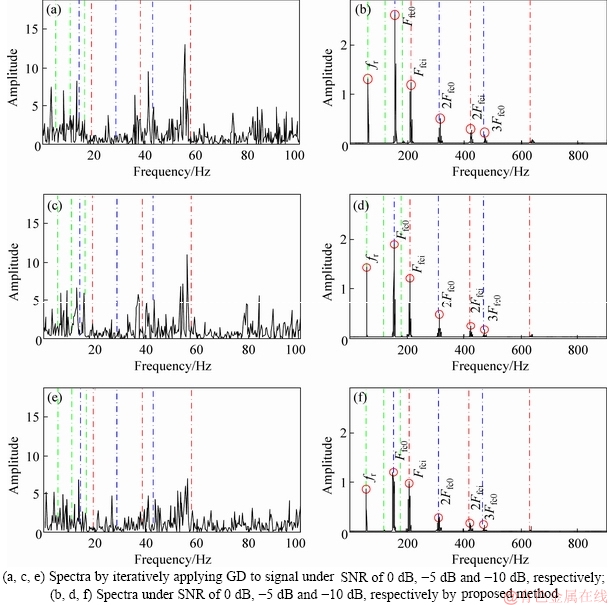
Figure 3 Demodulation spectra under different noise levels:

Unlike the E-factor configuration method in the simulated signal, the E-factor cannot be set to the maximum value of target instantaneous frequency, considering the fitting error in the endpoint of the frequency trend line. The E-factors of different components are set to the instantaneous frequency values at time t=4.5 s. Figure 5(f) shows the demodulation spectrum via the proposed method, in which some prominent peaks clearly appear at outer race fault characteristic frequency F_fc0, inner race fault characteristic frequency F_cfi, modulation rotating frequency f_r, as well as their harmonics. This further demonstrates the effectiveness of the proposed method in precisely pinpointing the characteristic frequency components of multi-fault bearing.

To validate the superiority of the proposed method, the experimental signal is also analyzed by other commonly used demodulation methods. Figure 6(a) shows the IFCF extracted by peak search method from the envelope time-frequency representation. Although the extracted instantaneous frequency exhibits a regular change rule, it cannot be utilized to accurately estimate the phase function due to the random variation in the low frequency region as well as the unpredictable rotating frequency trend in factual application.

Figure 4 Experimental setup (a), fault bearing (b) and defect (c)

Table 2 Parameters of rolling element bearing

Figure 6(b) shows the demodulation spectrum obtained by applying GD to the vibration signal guided by the peak search based IFCF. It can be observed that no prominent peak appears as expect. Figure 6(c) shows the demodulation spectrum generated by iteratively adopting GD to the signal with the phase functions of the peak search based IFCF and the characteristic coefficients of the test bearing.From this figure, no obvious peak is revealed. Figures 6(d) and (e) show the spectrums by utilizing GD and iteratively applying GD to the signal guided by the chirplet path pursuit. From Figure 6(d), it can be found that one peak is revealed, however, the location is far from the calculated value. In Figure 6(e), several peaks are found, however, the frequency values are deviated from the theoretical characteristic frequencies and the peaks are surrounded with noise. Hence, the traditional method failed in pinpointing the fault pattern, even guided by the chirplet path pursuit. Figure 6(f) shows the spectrum via GDTEF. From this figure, although one peak accurately appears at its theoretical location, the multi-fault cannot be indicated by the only one peak. The comparison results confirm the superiority of the proposed method.

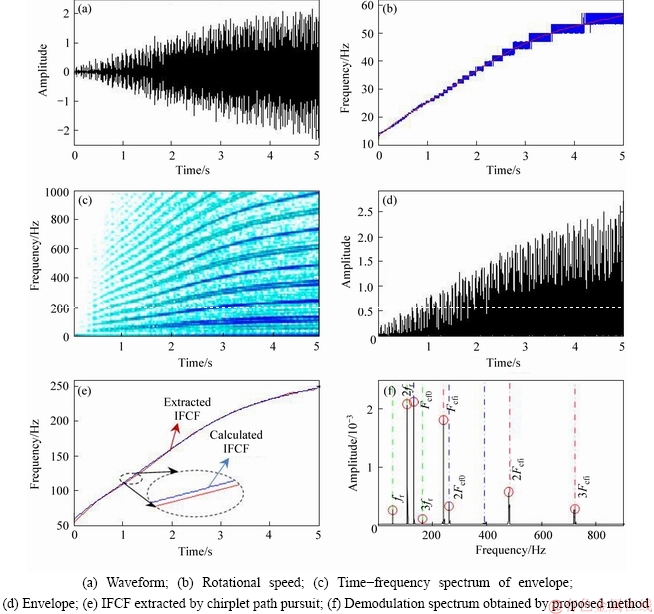
Figure 5 Experimental case:

5 Conclusions

Considering the time-varying behavior and the complex sideband structures of multi-fault bearing signals under nonstationary conditions, the enhanced demodulation spectrum analysis method for bearing fault detection via chirplet path pursuit is proposed. The characteristic frequency can be accurately extracted free from the interferences of different faults, by exploiting the unique merits of chirplet path pursuit. The complex sidebands can be effectively avoided by the enhanced demodulation spectrum, which simplifies the characteristic frequency identification. The method is validated by simulated and experimental data. The results show that it gives a faithful and accurate rendering of the frequency representation of the nonstationary signal, and therefore it is easily applied to bearing fault detection.

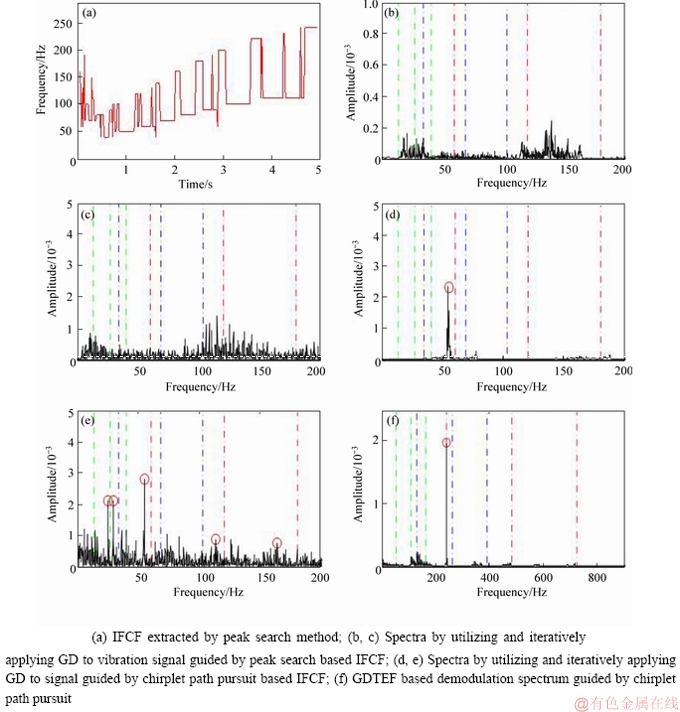
Figure 6 Comparison results:

References

[1] GUO Yu, LIU Ting-wei, NA Jing, FUNG Rong-fong. Envelope order tracking for fault detection in rolling element bearings [J]. Journal of Sound and Vibration, 2012, 331(25): 5644-5654. DOI: 10.1016/j.jsv. 2012.07.026.

[2] XIANG Jia-wei, ZHONG Yong-teng, GAO Hai-feng. Rolling element bearing fault detection using PPCA and spectral kurtosis [J]. Measurement, 2015, 75: 180-191. DOI: 10.1016/j.measurement. 2015.07.045.

[3] FENG Zhi-peng, CHEN Xiao-wang, WANG Tian-yang. Time-varying demodulation analysis for rolling bearing fault diagnosis under variable speed conditions [J]. Journal of Sound and Vibration, 2017, 400: 71-85. DOI: 10.1016/j.jsv.2017.03.037.

[4] FENG Zhi-peng, LIANG Ming, CHU Fu-lei. Recent advances in time-frequency analysis methods for machinery fault diagnosis: A review with application examples [J]. Mechanical Systems and Signal Processing, 2013, 38(1): 165-205. DOI: 10.1016/j.ymssp.2013.01. 017.

[5] WANG Chun-sheng, SHA Chun-yang, SU Mei, HU Yu-kun. An algorithm to remove noise from locomotive bearing vibration signal based on self-adaptive EEMD filter [J]. Journal of Central South University, 2017, 24(2): 478-488. DOI: 10.1007/s11771-017-3450-8.

[6] Antoni J, Randall R B. The spectral kurtosis application to the vibratory surveillance and diagnostics of rotating machines [J]. Mechanical Systems and Signal Processing, 2006, 20(2): 308-331. DOI: 10.1016/j. ymssp.2004.09.002.

[7] WANG Yan-xue, XIANG Jia-wei, RICHARD M, LIANG Ming. Spectral kurtosis for fault detection, diagnosis and prognostics of rotating machines: A review with applications [J]. Mechanical Systems and Signal Processing, 2016, 66-67: 679-698. DOI: 10.1016/j.ymssp. 2015.04.039.

[8] YU De-jie, WANG Min, CHENG Xiang-min. A method for the compound fault diagnosis of gearboxes based on morphological component analysis [J]. Measurement, 2016, 91: 519-531. DOI: 10.1016/j.measurement.2016.05.087.

[9] PURUSHOTHAM V, NARAYANAN S, PRASAD S A N. Multi-fault diagnosis of rolling bearing elements using wavelet analysis and hidden Markov model based fault recognition [J]. NDT and E International, 2005, 38(8): 654-664. DOI: 10.1016/j.ndteint.2005.04 003.

[10] TENG Wei, DING Xian, ZHANG Xiao-long, LIU Yi-bing, MA Zhi-yong. Multi-fault detection and failure analysis of wind turbine gearbox using complex wavelet transform [J]. Renewable Energy, 2016, 93: 591-598. DOI: 10.1016/ j.renene.2016.03.025.

[11] CHEN Fa-fa, Tang Bao-ping, Song Tao, Li Li. Multi-fault diagnosis study on roller bearing based on multi-kernel support vector machine with chaotic particle swarm optimization [J]. Measurement, 2014, 47(1): 576-590. DOI: 10.1016/j.measurement.2013.08.021.

[12] HE Shui-long, CHEN Jing-long, ZHOU Zi-tong, ZI Yan-yang, WANG Yan-xue, WANG Xiao-dong. Multifractal entropy based adaptive multiwavelet construction and its application for mechanical compound-fault diagnosis [J]. Mechanical Systems and Signal Processing, 2016, 76-77: 742-758. DOI: 10.1016/j.ymssp.2016.02. 061.

[13] JIANG Hong-kai, LI Cheng-liang, LI Hua-xing. An improved EEMD with multiwavelet packet for rotating machinery multi-fault diagnosis [J]. Mechanical Systems and Signal Processing, 2013, 36(2): 225-239. DOI: 10.1016/ j.ymssp. 2012.12.010.

[14] Li Zhi-xiong, Yan Xin-ping, Yuan Cheng-qing, Peng Zhong-xiao, Li Li. Virtual prototype and experimental research on gear multi-fault diagnosis using wavelet- autoregressive model and principal component analysis method [J]. Mechanical Systems and Signal Processing, 2011, 25(7): 2589-2607. DOI: 10.1016/j.ymssp. 2011.02. 017.

[15] Patel V N, Tandon N, Pandey R K. A dynamic model for vibration studies of deep groove ball bearings considering single and multiple defects in races [J]. Journal of Tribology, 2010, 132(4): 041101. DOI: 10.1115/1.4002333.

[16] Cao Hong-rui, Niu Lin-kai, He Zheng-jia. Method for vibration response simulation and sensor placement optimization of a machine tool spindle system with a bearing defect [J]. Sensors, 2012, 12(7): 8732-8754. DOI: 10. 3390/s120708732.

[17] Wang Tian-yang, Liang Ming, LI Jian-yong, Cheng Wei-dong, Li Chuan. Bearing fault diagnosis under unknown variable speed via gear noise cancellation and rotational order sideband identification [J]. Mechanical Systems and Signal Processing, 2015, 62-63: 30-53. DOI: 10.1016/ j.ymssp.2015.03.005.

[18] Yang Yu, Wang Huan-huan, Cheng Jun-sheng, Zhang Kang. A fault diagnosis approach for roller bearing based on VPMCD under;variable speed condition [J]. Measurement, 2013, 46(8): 2306-2312. DOI: 10.1016/j.measurement.2013. 03.023.

[19] Li Yong-zhuo, Ding Kang, He Guo-lin, Jiao Xin-tao. Non-stationary vibration feature extraction method based on sparse decomposition and order tracking for gearbox fault diagnosis [J]. Measurement, 2018, 124: 453-469. DOI: 10.1016/j.measurement.2018. 04.063.

[20] Zhao Ming, Lin Jing, Wang Xiu-feng, Lei Ya-guo, Cao Jun-yi. A tacho-less order tracking technique for large speed variations [J]. Mechanical Systems and Signal Processing, 2013, 40(1): 76-90. DOI: 10.1016/j.ymssp.2013.03.024.

[21] Wang Yi, Xu Guang-hua, Luo Ai-ling, Liang Lin, Jiang Kuo-sheng. An online tacholess order tracking technique based on generalized demodulation for rolling bearing fault detection [J]. Journal of Sound and Vibration, 2016, 367(14): 233-249. DOI: 10.1016/j.jsv.2015.12.041.

[22] Zhao De-zun, Li Jian-yong, Cheng Wei-dong, Wang Tian-yang, Wen Wei-gang. Rolling element bearing instantaneous rotational frequency estimation based on EMD soft-thresholding denoising and instantaneous fault characteristic frequency [J]. Journal of Central South University, 2016, 23(7): 1682-1689. DOI: 10.1007/s11771- 016-3222-x.

[23] Shi Juan-juan, Liang Ming, Guan Yun-peng. Bearing fault diagnosis under variable rotational speed via the joint application of windowed fractal dimension transform and generalized demodulation: A method free from prefiltering and resampling [J]. Mechanical Systems and Signal Processing, 2016, 68-69(6): 15-33. DOI: 10.1016/j.ymssp. 2015. 08.019.

[24] Feng Zhi-peng, Chen Xiao-wang, Liang Ming. Joint envelope and frequency order spectrum analysis based on iterative generalized demodulation for planetary gearbox fault diagnosis under nonstationary conditions [J]. Mechanical Systems and Signal Processing, 2016, 76-77: 242-264. DOI: 10.1016/j.ymssp.2016.02. 047.

[25] Cheng Wei-dong, Gao R X, Wang Jin-jiang, Wang Tian-yang, Wen Wei-gang, Li Jian-yong. Envelope deformation in computed order tracking and error in order analysis [J]. Mechanical Systems and Signal Processing, 2014, 48(1, 2): 92-102. DOI: 10.1016/j. ymssp.2014.03.004.

[26] Combet F, Zimroz R. A new method for the estimation of the instantaneous speed relative fluctuation in a vibration signal based on the short time scale transform [J]. Mechanical Systems and Signal Processing, 2009, 23(4): 1382-1397. DOI: 10.1016/j.ymssp.2008.07. 001.

[27] Urbanek J, Barszcz T, Antoni J. A two-step procedure for estimation of instantaneous rotational speed with large fluctuations [J]. Mechanical Systems and Signal Processing, 2013, 38(1): 96-102. DOI: 10.1016/j.ymssp. 2012.05.009.

[28] Wang Tian-yang, Liang Ming, Li Jian-yong, Cheng Wei-dong. Rolling element bearing fault diagnosis via fault characteristic order (FCO) analysis [J]. Mechanical Systems and Signal Processing, 2014, 45(1): 139-153. DOI: 10.1016/ j.ymssp.2013.11.011.

[29] LIU Dong-dong, CHENG Wei-dong, WEN Wei-gang. Rolling bearing fault diagnosis via ConceFT-based time-frequency reconfiguration order spectrum analysis [J]. IEEE Access, 2018, 6(1): 1-13. DOI: 10.1109/ACCESS. 2018.2877711.

[30] CandES E J, Charlton P R, Helgason H. Detecting highly oscillatory signals by chirplet path pursuit [J]. Applied and Computational Harmonic Analysis, 2008, 24(1): 14-40. DOI: 10.1016/j.acha.2007.04.003.

[31] Olhede S, Walden A T. A generalized demodulation approach to time-frequency projections for multicomponent signals [J]. Proceedings Mathematical Physical and Engineering Sciences, 2005, 461(2059): 2159-2179. DOI: 10.1098/rspa. 2005.1455.

[32] LIU Dong-dong, Cheng Wei-dong, Wen Wei-gang. Generalized demodulation with tunable E-Factor for rolling bearing diagnosis under time-varying rotational speed [J]. Journal of Sound and Vibration, 2018, 430(15): 59-74. DOI: 10.1016/j.jsv.2018.05.026.

(Edited by FANG Jing-hua)

中文导读

基于线调频小波路径追踪的多故障轴承解调频谱分析

摘要：由于非平稳工况下多故障轴承复杂调制特征的影响，使得识别故障特征频率十分困难。为了消除振动信号时变工况影响，必须获得特征频率的相位函数。然而，多故障的特征频率之间互相干扰，影响了瞬时频的提取。因此，本文提出一种基于线调频小波路径追踪的多故障轴承改进解调频谱分析方法。对原始信号进行Hilbert变换得到包络信号；使用线调频小波路径追踪算法从包络信号提取特征频率，并且根据特征系数计算其他特征频率；根据振动信号的时变特征计算各成分的能量因子；迭代使用能量因子可调广义解调算法和带通滤波器获得解调信号；对解调信号进行频谱分析，识别轴承特征频率。仿真和试验信号的分析验证了该算法的有效性。

关键词：滚动轴承；解调频谱；多故障检测；非平稳；线调频小波路径追踪

Foundation item: Project(2018YJS137) supported by the Fundamental Research Funds for the Central Universities, China; Project(51275030) supported by the National Natural Science Foundation of China

Received date: 2018-07-01; Accepted date: 2018-11-13

Corresponding author: CHENG Wei-dong, PhD, Professor; Tel: +86-10-51687004; E-mail: wdcheng@bjtu.edu.cn; ORCID: 0000-0001- 5085-4758