H_∞ control of networked control system with packet dropouts and its application on simulation platform with NS2

WANG Qing-feng(王庆凤)¹, CHEN Hong(陈虹)², WANG Hong-bo(王红波)¹

(1. College of Electronic Science and Engineering, Jilin University, Changchun 130012, China;

2. Department of Control Science and Engineering, Jilin University, Changchun 130025, China)

Abstract: The problem of data packet dropouts induced by communication channel in networked control systems (NCS) was studied. NCS with packet dropouts was modeled as Markov jump linear system (MJLS) and the H_∞ control techniques of NCS were established based upon the bounded real lemma of MJLS. The state feedback controller was computed by a necessary and sufficient linear matrix inequality condition. Using the software NS2 to simulate real network performance, we designed and implemented a new real-time simulation platform for NCS. An experiment was carried out on the platform and the simulations have demonstrated the effectiveness of the proposed approach.

Key words: networked control system; data packet dropout; H_∞ control; Markov jump linear system; NS2

CLC number: TP273            Document code: A            Article ID: 1672-7207(2011)S1-0380-06

1 Introduction

Recently, much attention has been paid to the study of stability analysis and control design of networked control systems^[1-2], due to their low cost, reduced mass and power requirements, simple installation and maintenance, and high reliability. Packet dropout is one of the most important and special issues of networked control systems (NCS). Some results have been available. In Refs.[1, 3], NCS with packet dropouts are modeled as asynchronous switched systems. The approach replaces the true switched system with an “averaged” system and then studies the stability property. In Ref.[4] packet dropout process is modeled as an arbitrary but finite switching signal. This enables them to apply the results from switched systems to stabilize NCS. With packet dropout rate known and constant, NCS is formulated as a Markov jump system with two operation modes^[5]. A dynamic output feedback controller design method was proposed such that NCS is mean square stable and has H_∞ gain as a function of packet dropout below a certain value. However, in the framework considered above, the controller is directly connected to the actuator. A general framework was considered in Ref.[6], where both sampling signals and control commands are transmitted through the network and may be dropped during the transmissions. The linear quadratic Gaussian control problem was studied based on dynamic programming approach. In Ref.[7], the stability conditions of networked control systems with Markov packet dropout process are established via a packet dropout dependent Lyapunov approach. However, the H_∞ performance is not considered.

Simulations and experiments are necessary to invalidate the networked control schemes. The existent simulation platforms^[8-9] have some disadvantages in flexibility or validity. They can only perform parts of network performance or/and cannot simulate various network topologies.

In this work, we consider the stabilization and H_∞ control problem of NCS. The packet dropout process is considered as Markov packet dropout process. With a freedom matrix introduced, the stabilizing controller design techniques can be constructed in terms of linear matrix inequalities (LMIs). The H_∞ control techniques of NCS are established based upon the bounded real lemma of MJLS and the state feedback controller is computed by a necessary and sufficient linear matrix inequality condition. Finally, using the software NS2 to simulate real network performance, we designed and implemented a real-time simulation platform for NCS. An experiment was carried out and the simulations have demonstrated the effectiveness of the proposed approach.

2 Problem description

An NCS with packet dropout consists of a discrete-time system and a discrete-time controller:

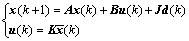       (1)

where x(k)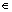Rⁿ, u(k)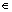R^m are the state vector and the input vector, respectively; d(k) is the disturbance vector; K is the state feedback gain matrix to be designed;  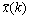is the input of the controller. Both sampling signals and control commands are transmitted through the network. The sampler is clock driven, the controller and zero- order holder are event driven and the data are transmitted in a single packet at each time step. The data packets may be dropped during the transmissions when node failures or message collisions happen.

Only when both sampling signal and control command are transmitted successfully, we can say that the data from sampler to zero-order holder is not dropped. So, assume that data packets are transmitted at sparse steps k_i (i=1, 2, …), the quantity of data packet dropout 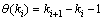 between two successful data transmission steps takes values in the finite state space

Ω={0, 1, 2, …, N}, where 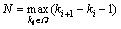 is the

maximum packet drop-out upper bound.

From the viewpoint of the zero-order hold, the control input is

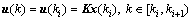
Suppose that the disturbance does not vary between two successful transitions, i.e.

.

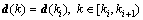With data packet containing the state measurement transmitted in a stochastic distribution described as above, the plant can be modeled as the following iteratively:

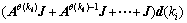      (2)

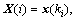
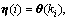
Define 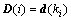and

,

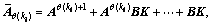
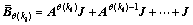then we have

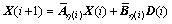        (3)

The system performance output is given as

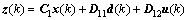       (4)

then we have

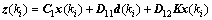     (5)

Define Z(i)=z(k_i), we have

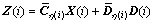          (6)

where 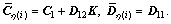 To establish contact with jump linear system, the matrices of closed NCS are denoted with the subscript η(i) although  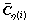and 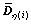 are definite and constant.

So, the closed NCS with Markov packet dropout process can be modeled as the following stochastic system:

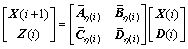      (7)

The state matrices are functions of a discrete-time Markov chain taking values in a finite set Ω={0, 1, 2, …, N}. Plants of this form are called discrete-time Markov jump linear systems^[10].

3 Stabilization of NCS

We consider the general jump linear system

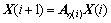            (8)

The Markov integer jump parameter η(i)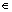Ω and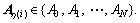 

Below, we present necessary and sufficient matrix inequality conditions on mean square stable of the system (8).

Lemma 1: NCS (8) is mean square stable if and only if there exist symmetric positive matrices Q_i, i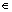Ω such that

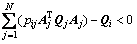
holds for all i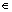Ω.

However, finding a constant state feedback controller for discrete-time Markov jump linear systems with a non-accessible jumping parameter is a difficult problem. With a freedom matrix G introduced, we will develop sufficient conditions on the stabilization of the NCS.

Lemma 2^[7]: The system (8) is mean square stable if there exist matrices Q_i>0 and a matrix G for i=0, 1, …, N satisfying the following conditions:

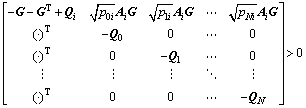(9)

where (·)^T denote entries  which  can  be  inferred  from the symmetry of the matrix.

The introduction of the freedom matrix G enables one to write stability conditions which are less conservative due to the presence of the extra degree of freedom. We will look for a constant state  feedback gain K such that  the NCS (1)  is  mean  square  stable  for  data  packet dropout  governed  by a Markov chain .

Theorem 1: Considering discrete-time system (1), there exists a state-feedback controller K, over network with Markov packet dropout process, such that NCS (1) is mean square stable if there exist symmetric positive matrices Q_i, i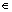Ω, G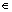R^n×n, and Y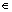R^m×n, satisfying the coupled LMIs:

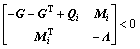          (10)

for all i, j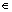Ω, where

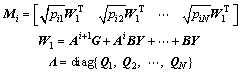
The controller is given by K=YG^-1.

Proof: Using the definition of Eq.(2), Schur complementary and the change of variable Y=KG,  Eq.(10) is direct corollary of Eq.(9).

4 H_∞ controller design

Consider the following Markov Jump Linear system, denoted P

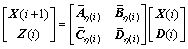      (11)

The Markov chain has transition probability p_ij= Pr(η(k+1)=j|η(k)=i), which is subjected to the restrictions

p_ij≥0 and 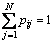 for any i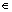Ω. The plant initial

conditions are given by specifying X₀, θ₀.

Assume that P is a mean square stable system. Let X(0)=X₀ and define the H_∞ norm, denoted as

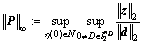         (12)

where l₂ is defined as the space of square assumable (stochastic) sequences. The H_∞ norm is defined as the maximum input-output gain with the appropriately defined 2 norms.

In this section, we consider NCS with Markov packet dropout process satisfies p_ij=p_j, i.e. that the packet is transmitted successfully or not at the time j is independent of that at the previous instance.

Lemma 3 (Bounded Real Lemma)^[10]: Assume p_ij= p_j for all i, j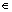Ω and the system P is weakly controllable. System P is mean square stable and ||P||_∞<γ, if and only if there exist a symmetric matrices G>0 that satisfy:

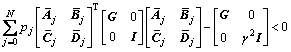  (13)

We will apply Lemma 3 to derive an LMI condition for controller synthesis.

Theorem 2: Assume p_ij=p_j for all i, j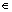Ω and the system is weakly controllable. System P is mean square stable and ||P||_∞<γ, if and only if there exist a symmetric matrix Z>0 and a matrix Q that satisfy:

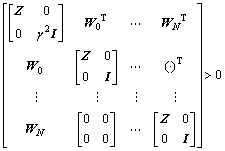  (14)

where

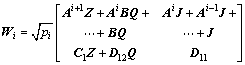  (15)

The controller is given by K=QZ^-1.

Proof: Let Z=G^-1 and multiply equation above on

the left and right by  Since definiteness is

invariant under congruence transformations, Eq.(13) is equivalent to:

Use the Schur complement lemma to convert this inequality into the following equivalent condition:

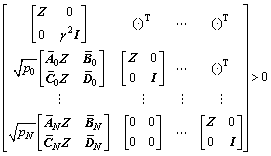        (16)

This is a bilinear matrix inequality since it is linear in the controller parameters (for a fixed scaling matrix) or in Z (for fixed controller matrices). With the matrices 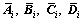defined before for NCS with Markov packet dropout process and the change of variable Q=KZ, we have the theorem 2.

5 Simulation platform based on NS2

Using network simulation software NS2 to simulate the real network performance, we designed and realized a real-time simulation platform for networked control systems. The framework of our simulation platform is shown in Fig.1 with four blocks which are Matlab/ Simulink plant and controller block, Matlab data interface block, Java network interface block and network simulation block. We use Matlab to simulate the real time control system and NS2 to simulate the real network. The communication between NS2 and Matlab is realized by Java application. Combined with the virtues of NS2 and Matlab, the platform realizes the co-simulation of control system and network. And also the platform can simulate various network performances veritably, and provide the simulating and experiment condition for the study of the stability and performance of NCS.

The platform can simulate various network performances veritably, for example, the network topology can be described with parameters as shown in Fig.2. The data from the plant can be transmitted to the controller through network. Running for 30 min on the platform of NCS with the sampling time of 0.1 s, the network performance of packet dropout and delay are obtained. The time delays are not zero, but 94.51% are less than 0.03 s. After data processing, we have the maximum packet dropout upper bound N=8, and P= [0.632 7, 0.209 1, 0.093 4, 0.037 8, 0.016 1, 0.007 4, 0.002 5, 0.008, 0.000 3], which means that 38.77% of the packets  can  be  lost  during  the  network transmissions.

6 Simulation example

Considering the cart and inverted pendulum problem^[11], the state variables are 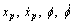, After linearization under equilibrium point (f=0), we have the continuous linear equation:

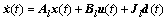
Take the sampling time h=0.1 s and we have the discrete model as Eq.(1). Take K₁=[0.400 5, 9.825 1, 25.447 8, 4.821 9], the closed point to point system is stable. However, for the closed loop control system through network with the state feedback controller A+BK₁ and initial skewing angle of 6.7°, the system outputs are shown in Fig.3. It is obvious that even though the performance of network is not great, the system is unstable in a short time.

Applying Theorem 1, we obtain a networked controller K₂=[0.335 4, 10.522 3, 33.782 0, 5.255 0]. Impose a disturbance d=5sint to the system with zero initial condition and Applying Theorem 2, we obtain a networked H_∞ controller K₃=[1.686 2, 11.754 9, 37.125 7, 5.825 5]. The outputs responses are shown in Fig.4 and Fig.5, from which we can see that the system has good performance with the designed H_∞ state feedback controller.

The obtained results are derived based on the assumption that the disturbance does not vary between two successful transmissions. The interval between two successful transmissions is the new sampling time for discrete closed NCS with packet dropout. It is reasonable to hold each value for one sample interval while controller designing.

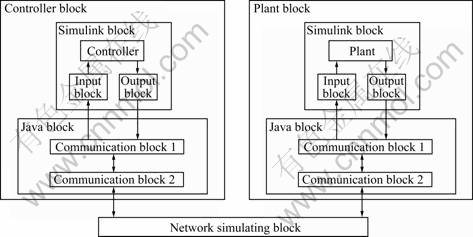
Fig.1 Framework of simulation platform

Fig.2 Network topology

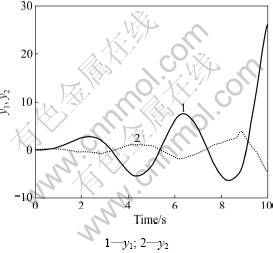
Fig.3 System outputs when using controller K₁

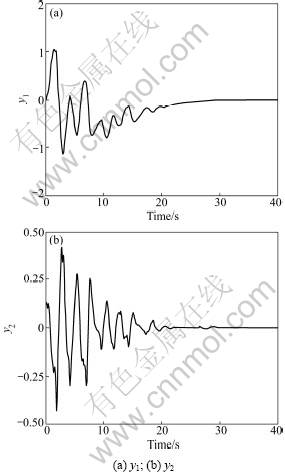
Fig.4 System outputs using controller K₂

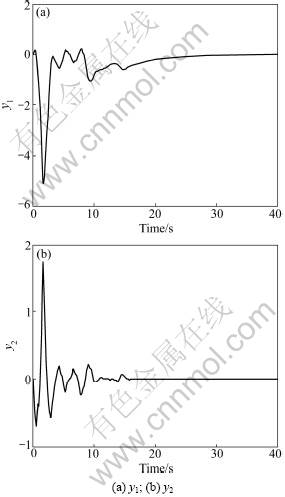
Fig.5 System outputs using controller K₃

7 Conclusions

We have investigated mean square stabilization of a class of networked control system with data packet dropout induced by network channels. With a freedom matrix introduced, we develop sufficient conditions on the stabilization of the NCS. Networked control system performance is measured via an H_∞ norm and the state feedback controller is computed by a necessary and sufficient LMIs condition. A new simulation platform designed and implemented based on NS2 can simulate various network performance veritably and effectively. The results are applied to an inverted pendulum system and simulations demonstrate the proposed method works well.

References

[1] Zhang W, Branicky M S, Phillips S M. Stability of networked control systems[J]. IEEE Control Systems Magazine, 2001, 21(1): 84-99.

[2] Goodwin G C, Silva E I, Quevedo D E. Analysis and design of networked control systems using the additive noise model methodology A[J]. Asian Journal of Control, 2010, 12(4): 443-459.

[3] Qiang L, Micheal D L. Power spectral analysis of networked control systems with data dropouts[J]. IEEE Transactions on Automatic Control, 2004, 49(6): 955-959.

[4] Yu M, Wang L, Chu T, et al. Stabilization of networked control systems with data packet dropout and network delays via switching system approach[C]//Proceedings of the 43rd IEEE Conference on Decision and Control. 2004: 3539-3544.

[5] Seiler P, Sengupta R. An H_∞ approach to networked control [J]. IEEE Transactions on Automatic Control, 2005, 50(3): 354-364.

[6] Fang X, Wang J. Stochastic observer-based guaranteed cost control for networked control systems with packet dropouts[J]. IET Control Theory and Applications, 2008, 2(11): 980-989.

[7] Xiong J L, Lam J. Stabilization of linear systems over networks with bounded packet loss [J]. Automatica, 2007, 43(26): 80-87.

[8] Ma X H, Wei Z, Xie J Y. Simulation platform of networked control systems based on canbus[J]. Journal of System Simulation, 2005, 17(1): 100-103.

[9] Yuan G, Cong S, Chen Q G, et al. Design of the simulation platform for networked control systems based on DTHMM[C]//Proceedings of the 8th World Congress on Intelligent Control and Automation (WCICA). 2010: 4400-4406.

[10] Seiler P, Raja S. A bounded real lemma for jump systems[J]. IEEE Transactions on Automatic Control, 2009, 48(9): 1651-1654.

[11] WANG Qing-feng, CHEN Hong. H_∞ control of networked control system with long time delay[C]//Proceedings of the 7th World Congress on Intelligent Control and Automation. China: Chong-qing, 2008: 5453-5456.

(Edited by YANG Bing)

Received date: 2011-04-15; Accepted date: 2011-06-15

Foundation item: Project(450060445138) supported by Fundamental Research Funds for the Central Universities in China; Project(60725311) supported by the National Natural Science Foundation of China for Distinguished Young Scholar

Corresponding author: WANG Qing-feng, PhD; Tel: +86-13756628334; E-mail: wangqf@jlu.edu.cn