J. Cent. South Univ. Technol. (2011) 18: 1161-1168

DOI: 10.1007/s11771-011-0818-z

Consensus and formation control of discrete-time multi-agent systems

WANG Jing(王婧), NIAN Xiao-hong(年晓红), WANG Hai-bo(王海波)

School of Information Science and Engineering, Central South University, Changsha 410083, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: Consensus problems for discrete-time multi-agent systems were focused on. In order to design effective consensus protocols, which were aimed at ensuring that the concerned states of agents converged to a common value, a new consensus protocol for general discrete-time multi-agent system was proposed based on Lyapunov stability theory. For discrete-time multi-agent systems with desired trajectory, trajectory tracking and formation control problems were studied. The main idea of trajectory tracking problems was to design trajectory controller such that each agent tracked desired trajectory. For a type of formation problem with fixed formation structure, the formation structure set was introduced. According to the formation structure set, each agent can track its individual desired trajectory. Finally, simulations were provided to demonstrate the effectiveness of the theoretical results. The numerical results show that the states of agents converge to zero with consensus protocol, which is said to achieve a consensus asymptotically. In addition, through designing appropriate trajectory controllers, the simulation results show that agents converge to the desired trajectory asymptotically and can form different formations.

Key words: multi-agent system; consensus; trajectory tracking; formation

1 Introduction

Multi-agent systems have broad applications in many areas including cooperative control of unmanned air vehicles (UAVs), flocking, distributed sensor networks, attitude alignment of clusters of satellites, and congestion control in communication networks. Specially, in the military field, natural extensions to multi-agent systems are the traditional trajectory tracking and formation control [1-2].

Consensus problem is a comprehensive interdisciplinary subject, including control theory, mathematics, biology, physics, computer science, robotics, artificial intelligence and so on. In networked multi-agent systems, “consensus” means to reach an agreement regarding a certain quantity of interest that depends on the states of all agents. A “consensus protocol” is an interaction rule that specifies the information exchange between an agent and all of its neighbors on the network [3-5]. In the past few years, consensus problems of multi-agent systems have been developed very fast and several research topics have been addressed, such as finite-time consensus [6-7], networks with switching topologies and fixed topologies [8-10], formation [1-2], and asynchronous consensus  [11-13].

Numerous approaches to the consensus problem of multi-agent systems have been reported. For example, based on the frequency-domain analysis, TIAN et al [14-16] have studied the consensus problems for first-order and second-order multi-agent systems with diverse input delays and communication delays. Utilizing the concept of cross-coupling approach, the basic idea of Ref.[17] is that a team of mobile robots track each individual’s desired trajectory while synchronizing motions among the robots to keep relative kinematics relationship for maintaining the desired, and perhaps time-varying formation. The work in Ref.[18] focuses on consensus problem for networks of dynamic agents with fixed and switching topologies mainly relying on algebraic graph theory. In Ref.[19], the synchronization problem has been investigated for an array of coupled complex discrete-time networks with the simultaneous presence of both the discrete and distributed time delays, in which a more general sector-like nonlinear function is employed to describe the nonlinearities existing in the network. Up to now, in most of the existing work on consensus problem, low-dimensional (generally N=1 or  2) multi-agent systems have been studied. However, low-dimensional systems are impractical in many practical situations.

As an important theoretical preparation for the development of the main results, consensus theory is another interesting topic in decentralized control [3,6,18]. One main research issue in consensus problems is how to design effective consensus protocols, which are distributed interaction rules among agents and are aimed at ensuring that the concerned states of agents converge to a common value [3,6]. The typical discrete-time consensus protocol provided by JADBABAIE et al [20] is a simplified Vicsek model [21]. Later, REN et al [22-23] have extended it to the case with switching directed interaction topologies and proved that if the union of the interaction topologies has a spanning tree frequently enough as the system evolves, the information consensus can be achieved asympototically. Then, It is established [24] that consensus problems are solvable under the same topology conditions as the typical ones [20], without the requirement that agents always get their own instantaneous state information.

In this work, consensus problems for general discrete-time multi-agent systems were considered. The approach can be applied to both low-dimension and high-dimension multi-agent systems. Consensus, trajectory tracking and formation control of discrete-time multi-agent systems were mainly studied. The analysis relied on several tools such as Lyapunov stability theory, matrix theory, and control theory. First, a connection was established between the multi-agent systems and the information flow of directed graph. Based on the Lyapunov stability theory, the stability of multi-agent systems with the presented consensus protocols was analyzed. Then, consensus protocols were designed via linear matrix inequality (LMI) and bilinear matrix inequality (BMI) methods [25]. Second, assuming that multi-agent systems achieved consensus asymptotically, trajectory controllers were introduced. Each agent could track desired trajectory through trajectory controller. Last, a type of formation problems with fixed formation structure was studied. According to the formation structure set, each agent can track its individual’s desired trajectory. With the different formation structure sets, the agents can be in different formations. To verify the effectiveness of our theoretical results, simulations were performed.

2 Problem formulation

Let G=(V, ε, A) be a weighted digraph (or directed graph) of order n with the set of nodes V={v₁, …, v_n}, set of edges ε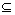v×v, and a weighted adjacency matrix A=[a_ij] with nonnegative adjacency elements a_ij. The node indexes belong to a finite index set ⊥={1, 2, …, n}. An edge of G is denoted by ε_ij=(v_i, v_j)ε. The set of neighbors of node v_i is denoted by N_i={v_jV:(v_i, v_j)ε}. Let x_iR^N denote the value of node v_i. We refer to G_x= (G, x) with x=(x₁, …, x_n)^T as a network (or a algebraic graph) with value x_iR^n×N and topology (or information flow) G. The value of a node might represent physical quantities including attitude, position, temperature, voltage and so on.

In the multi-agent systems with n agents, each agent can be considered as a node in a digraph, and the information flow between two agents can be regarded as a direct path between the nodes. Thus, the interconnection topology in the multi-agent systems can be described by a digraph G=(V, ε, A).

Let x_iR^N denote the state of agent i and suppose that the dynamics of agent i is described by the following discrete-time equation:

                              (1)

where A_iR^N×N denote the known self-loop matrix of agent i. u_iR^m×N is a state feedback, called protocol, to be designed.

Definition 1: Multi-agent system (Eq.(1)) is said to achieve a consensus asymptotically, if there exists consensus protocol u_i, such that

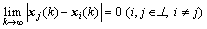
3 Consensus of multi-agent system

3.1 Consensus of multi-agent system

The consensus protocols that solve agreement problems for the multi-agent system are presented as

    (2)

where K_ijR^m×N are constant matrices to be designed. Then, the design problem of consensus protocols is transformed to solve gain matrix K_ij.

With consensus protocols (Eq.(2)), the closed-loop system of system is given by

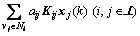                     (3)

For simplicity, let x=[x₁, x₂, …, x_n]^TR^n×N. Then, Eq.(3) can be rewritten as a vector form:

                                                          (4)

where

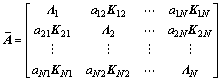
Theorem 1: Suppose that the communication topology G has a spanning tree. Under consensus protocols, the multi-agent system achieves a consensus asymptotically if there exist positive definite matrices P_ii (i), and matrices P_ij (j, iij (i, j), such that the following matrix inequalities hold:

Δ

                         (5)

Δ

                                 (6)

where

Proof: Consider the multi-agent system under consensus protocols, which is a multi-agent system. Choose a Lyapunov function:

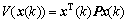
Define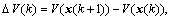 then along the solution of system, we have

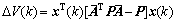
If the inequality holds

                                                             (7)

system achieves a consensus asymptotically. From the standard Schur complements, inequation (7) is equivalent to

                                            (8)

Pre-multiplying and post-multiplying by a positive definite block-diag matrix Diag[P, I], it follows that

                                             (9)

If K and P are replaced by their block-matrices in inequation (9), inequation (6) follows.

3.2 Algorithm of consensus protocol

Next, the design problem of consensus protocols is considered. From Theorem 1, the design problem of consensus protocols can be formulated as following problem with inequation constraints.

Problem 1:

This is a feasible problem of the LMI and BMI. If there exists a feasible solution of Problem 1, the multi-agent system achieves a consensus asymptotically. Since matrix inequation (6) is a BMI with variables P_ij and K_ij, if K_ij (or P_ij) is fixed, BMI can be formulated as LMI in matrix variables P_ij (or K_ij). Thus, the LMI toolbox can be used to calculate the feasible solution of these LMIs. Therefore, an obvious approach for solving Problem 1 is given by the following algorithm.

Algorithm 1:

1) Initialization: Let l=0, and give the initial values .

2) Repeat: Let l=l+1. By solving problem

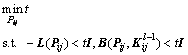
the solution  is obtained. Substitute them into problem

to obtain the solution 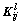 and denotes

3) Inequations 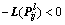 and  hold.

So far, a unified framework for analysis of convergence of consensus algorithms for directed networks with fixed topology in discrete-time has been presented. In this approach, gain matrix K_ij can be easily obtained through the selection of initial values.

4 Trajectory tracking of multi-agent systems

The basic idea is to design trajectory controllers d_i(k)R^N  for each agent to guarantee that the trajectory of each agent converges to desired trajectory asymptotically. Now, trajectory controllers d_i(k) are added to the consensus protocols. Then, the protocols are

        (10)

where d_i(k) is trajectory controllers to be designed.

Then, the multi-agent system is given as

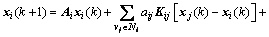
                                          (11)

Based on Theorem 1, suppose that the multi-agent system has achieved a consensus asymptotically. From Section 3, writing the closed-loop system of system in the vector form, we have got Eq.(4). Then, with Eqs.(4) and (11), multi-agent system can be written in the vector form as

                                       (12)

where .

For given trajectory f(k), suppose that system has achieved a consensus asymptotically and f(k) is bounded. Therefore, f(k) can be regarded as a special solution of system:

Let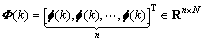

Utilizing Eq.(12), we have

                                           (13)

Then, trajectory controllers d_i(k) can be determined by

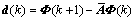                                  (14)

Theorem 2: Suppose that the communication topology G has a spanning tree. If the multi-agent system under consensus protocol has achieved a consensus asymptotically, then the agents in the system under trajectory controllers d_i(k) converge to the desired trajectory f(k) asymptotically, i.e.

                                (15)

where f(k) is bounded.

Proof: With multi-agent system, following equation is achieved by subtracting Eq.(13) from Eq.(12):

                                               (16)

where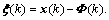

It is obvious that Eq.(16) is independent to trajectory controllers d_i(k). From Theorem 1, we know  is stable. Then, it is concluded that following equation holds:

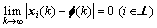
So, from Theorem 2, we can make the multi-agent system track any desired trajectory through designing appropriate trajectory controllers.

5 Formation control of multi-agent systems

A type of basic formation control problem is considered. First, define a formation structure set:

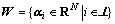
where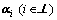is a constant vector.

Structure set W determines the formation of multi-agent. With the difference of structure set W, we can achieve different formations. For example, if formation of three agents with N=2 is equilateral triangle, the formation structure set can be given as

where a, b determine the desired position of agent 1 and r is the edge length of equilateral triangle.

Theorem 3: Suppose that the communication topology G has a spanning tree. If the multi-agent system under consensus protocol has achieved a consensus asymptotically, then each agent in the system under trajectory controllers d_i(k) converge to its individual desired trajectory f(k)+α_i asymptotically, i.e.

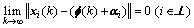              (17)

where α_i=W.

Proof: In fact, formation for multi-agent system with structure set W can be considered as a trajectory tracking problem where the desired trajectory for each agent is  When system has achieved a consensus asymptotically,  can be regarded as a special solution for system and f(k) is bounded. Denoteand 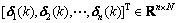. We have the following equation:

                                             (18)

Considering multi-agent system, following equation is achieved by subtracting Eq.(18) from Eq.(12):

where .

Then, the following equation is easily obtained:

6 Numerical examples

The simulation results are presented to illustrate the discrete-time consensus algorithm, trajectory tracking and formation. A multi-agent system with three agents is considered. The simulations are done for N=2 and 3.

Example 1: Consider the multi-agent system composed of three agents with the following parameters:

                                 (19)

where

With consensus protocol, assume that the weights of the edges are:Then, u_i(k)=

where K_ij are

real row vectors to be determined. Obviously, A₁, A₂ and A₃ are not all stable here. The initial values of state variables are

Let the initial values of K_ij be

By using Algorithm 1, feasible solutions are obtained as

 

With the parameters and the initial states chosen above, the agents in the system achieve a consensus asymptotically, as shown in Fig.1.

Example 2: Consider the multi-agent system of three agents with the same interconnection topology as Example 1, which is described by the following equation:

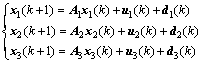                      (20)

Fig.1 2D positions of agents with consensus controllers

For simplicity, the same A_i is chose as given in Example 1. The initial values of state variables are

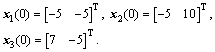
From Theorem 1 and Example 1, the system has achieved a consensus asymptotically. A desired trajectory f(k) is given as a ellipse, where

From Theorem 2, the agents in Eq.(20) converge to the desired trajectory asymptotically, as shown in Fig.2.

Fig.2 2D positions of agents with trajectory synchronous

Example 3: Consider the multi-agent system of three agents with the same interconnection topology as Example 2, which is described by Eq.(20). From Example 1, the system has achieved a consensus asymptotically. Let f(k) still be an ellipse, where

The initial values of state variables are

For example, from Theorem 3, when formation structure set

the agents in Eq.(20) are in formation and converge to their desired trajectory  asymptotically, as shown in Fig.3.

Fig.3 2D positions of agents with formation controllers

Example 4: Consider the multi-agent system composed of three agents with the following parameters:

                              (21)

where

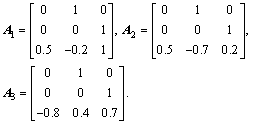
With consensus protocol, assume that the weights of the edges are  Then,

where K_ij are real row vectors to be determined. Obviously, A₁, A₂ and A₃ are not all stable here. The initial values of state variables are

Let the initial values of K_ij be

By using Algorithm 1, a feasible solution is obtained as

With the parameters and the initial states chosen above, the agents in the system achieve a consensus asymptotically, as shown in Fig.4. From Fig.4, we can see that x_i(k) converges to zero, that is to say, the agents achieve a consensus asymptotically.

Example 5: Consider the multi-agent system of three agents with the same interconnection topology as Example 4, which is described by the following equation:

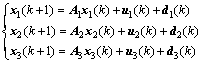                      (22)

Fig.4 State variables of agents with consensus controllers:    (a) Agent I; (b) Agent II; (c) Agent III

For simplicity, the same A_i is chosen as given in Example 4. The initial values of state variables are

From Theorem 1 and Example 4, the system has achieved a consensus asymptotically. We give desired trajectory f(k) as a helix line, where

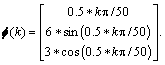
From Theorem 2, the agents in Eq.(22) converge to the desired trajectory asymptotically, as shown in Fig.5.

Example 6: Consider the multi-agent system of three agents with the same interconnection topology as Example 5, which is described by Eq.(22). From Example 4, the system has achieved a consensus asymptotically. Let f(k) be a curve, where

Fig.5 3D positions of agents with trajectory synchronous

For example, from Theorem 3, when formation structure set

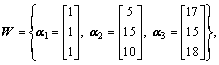
the agents in Eq.(22) are in formation and converge to their desired trajectory  asymptotically, as shown in Fig.6.

Fig.6 3D positions of agents with formation controllers

7 Conclusions

1) The consensus problems for discrete-time multi- agent systems are considered. Based on the Lyapunov stability theory, a new consensus protocol for general discrete-time multi-agent system is proposed.

2) The design problem of consensus protocols can be formulated as a feasible problem with LMI and BMI constraints, and the problem can be easily solved with the alternate algorithm. Furthermore, the design of trajectory controllers is proposed. With trajectory controllers, each agent can track individual desired trajectory. With different formation structure sets, agents can be in different formations.

3) The approach can be applied to both low- dimension and high-dimension multi-agent systems. Therefore, it is more realistic.

References

[1] EGERSTEDT M, HU Xiao-ming. Formation constrained multi-agent control [J]. IEEE Transactions on Robotics and Automation, 2001, 17(6): 947-951.

[2] LIN Zhi-yun, FRANCIS B, MAGGIORE M. Necessary and sufficient graphical conditions for formation control of unicycles [J]. IEEE Transactions on Automatic Control, 2005, 50(1): 121-127.

[3] OLFATI SABER R, FAX J A, MURRAY R M. Consensus and cooperation in networked multi-agent systems [J]. Proceedings of the IEEE, 2007, 95(1): 215-233.

[4] BENEDIKTSSON J A, SWAIN P H. Consensus theoretic classification methods [J]. IEEE Transactions Systems, Man, Cybernetics, 1992, 22(4): 688-704.

[5] OLFATI SABER R, MURRAY R M. Consensus protocols for networks of dynamic agents [C]// Proceedings of the American Control Conference. Denver, Colorado, 2003: 951-956.

[6] XIAO Feng, WANG Long, CHEN Jie, GAO Yan-ping. Finite-time formation control for multi-agent systems [J]. Automatica, 2009, 45: 2605-2611.

[7] XIAO Feng, WANG Long, JIA Ying-min. Fast information sharing in networks of autonomous agents [C]// Proceedings of 2008 American Control Conference. Seattle, 2008: 4388-4393.

[8] XIE Guang-ming, LIU Hui-yang, WANG Long, JIA Ying-min. Consensus in networked multi-agent systems via sampled control: Fixed topology case [C]// Proceedings of 2009 American Control Conference. St. Louis, 2009: 3902-3907.

[9] XIE Guang-ming, LIU Hui-yang, WANG Long, JIA Ying-min. Consensus in networked multi-agent systems via sampled control: Switching topology case [C]// Proceedings of 2009 American Control Conference. St. Louis, 2009: 4525-4530.

[10] LIU Bo, CHU Tian-guang, WANG Long, Xie Guang-ming. Controllability of a leader-follower dynamic network with switching topology [J]. IEEE Transactions on Automatic Control, 2008, 53(4): 1009-1013.

[11] LI Zhong-kui, DUAN Zhi-sheng, HUANG Lin. Leader-follower consensus of multi-agent systems [C]// Proceedings of 2009 American Control Conference. St. Louis, 2009: 3256-3261.

[12] LIN Zhi-yun, BROUCKE M, FRANCIS B. Local control strategies for groups of mobile autonomous agents [J]. IEEE Transactions on Automatic Control, 2004, 49(4): 622-629.

[13] YANG Peng, FREEMAN R A, LYNCH K M. Multi-agent coordination by decentralized estimation and control [J]. IEEE Transactions on Automatic Control, 2008, 53(11): 2480-2496.

[14] TIAN Yu-ping, LIU Cheng-lin. Robust consensus of multi-agent systems with diverse input delays and asymmetric interconnection perturbations [J]. Automatica, 2009, 45: 1347-1353.

[15] TIAN Yu-ping, LIU Cheng-lin. Consensus of multi-agent systems with diverse input and communication delays [J]. IEEE Transactions on Automatic Control, 2008, 53(9): 2122-2128.

[16] TIAN Yu-ping. Stability analysis and design of the second-order congestion control for networks with heterogeneous delays [J]. IEEE/ACM Transactions on Networking, 2005, 13(5): 1082-1093.

[17] SUN Dong, WANG Can, SHANG Wen, FENG Guang. A synchronization approach to trajectory tracking of multiple mobile robots while maintaining time-varying formations [J]. IEEE Transactions on Robotics, 2009, 25(5): 1074-1086.

[18] OLFATI SABER R, MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays [J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1520-1533.

[19] LIU Yu-rong, WANG Zi-dong, LIANG Jin-ling, LIU Xiao-hui. Synchronization and state estimation for discrete-time complex networks with distributed delays [J]. IEEE Transactions on Systems, Man and Cybernetics-Part B: Cybernetics, 2008, 38(5): 1314-1325.

[20] JADBABAIE A, LIN J, MORSE A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules [J]. IEEE Transactions on Automatic Control, 2003, 48(9): 988-1001.

[21] VICSEK T, CZIROK A, JACOB E B, COHEN I, SHOCHET O. Novel type of phase transitions in a system of self-driven particles [J]. Physical Review Letters, 1995, 75(6): 1226-1229.

[22] REN Wei, BEARD R W. Consensus seeking in multiagent systems under dynamically changing interaction topologies [J]. IEEE Transactions on Automatic Control, 2005, 50(5): 655-661.

[23] CAO Yong-can, REN Wei, LI Yan. Distributed discrete-time coordinated tracking with a time-varying reference state and limited communication [J]. Automatica, 2009, 45: 1299-1305.

[24] XIAO Feng, WANG Long. Consensus protocols for discrete-time multi-agent systems with time-varying delays [J]. Automatica, 2008, 44: 2577-2582.

[25] NIAN Xiao-hong, CAO Li. BMI approach to the interconnected stability and cooperative control of linear systems [J]. Acta Automatica Sinica, 2008, 34(4): 438-444.

(Edited by YANG Bing)

Foundation item: Projects(60474029, 60774045, 60604005) supported by the National Natural Science Foundation of China; Project supported by the Graduate Degree Thesis Innovation Foundation of Central South University, China

Received date: 2010-05-14; Accepted date: 2010-07-05

Corresponding author: NIAN Xiao-hong, Professor, PhD; Tel: +86-13549668182; E-mail: xhnian@mail.csu.edu.cn