Numerical simulation of liquid desiccant evaporator driven by heat pump
来源期刊:中南大学学报(英文版)2019年第8期
论文作者:牛润萍 陈潇义 王紫叶 匡大庆
文章页码:2197 - 2213
Key words:heat pump; condensation heat; discrete phase model (DPM); liquid desiccant evaporator; numerical simulation
Abstract: The standard k-? turbulence model and discrete phase model (DPM) were used to simulate the heat and mass transfer in a liquid-desiccant evaporator driven by a heat pump using FLUENT software, and the temperature field and velocity field in the device were obtained. The performance of the liquid-desiccant evaporator was studied as the concentration of the inlet solution varied between 21% and 30% and the pipe wall temperature between 30 and 50 °C. Results show that the humidification rate and the humidification efficiency increased with the inlet air temperature, the solution flow rate, the solution temperature, and the pipe wall temperature. The humidification rate and humidification efficiency decreased with increasing moisture content in inlet air and the concentration of inlet solution. The humidification rate increased substantially but the humidification efficiency decreased as the inlet air flow rate increased. The error between the simulations and experimental results is acceptable, meaning that our model can provide a theoretical basis for optimizing the performance of a humidifying evaporator.
Cite this article as: NIU Run-ping, CHEN Xiao-yi, WANG Zi-ye, KUANG Da-qing. Numerical simulation of liquid desiccant evaporator driven by heat pump [J]. Journal of Central South University, 2019, 26(8): 2197-2213. DOI: https://doi.org/10.1007/s11771-019-4166-8.

ARTICLE
J. Cent. South Univ. (2019) 26: 2197-2213
DOI: https://doi.org/10.1007/s11771-019-4166-8
NIU Run-ping(牛润萍), CHEN Xiao-yi(陈潇义), WANG Zi-ye(王紫叶), KUANG Da-qing(匡大庆)
School of Environment and Energy Engineering, Beijing University of Civil Engineering and Architecture,Beijing 100044, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: The standard k-ε turbulence model and discrete phase model (DPM) were used to simulate the heat and mass transfer in a liquid-desiccant evaporator driven by a heat pump using FLUENT software, and the temperature field and velocity field in the device were obtained. The performance of the liquid-desiccant evaporator was studied as the concentration of the inlet solution varied between 21% and 30% and the pipe wall temperature between 30 and 50 °C. Results show that the humidification rate and the humidification efficiency increased with the inlet air temperature, the solution flow rate, the solution temperature, and the pipe wall temperature. The humidification rate and humidification efficiency decreased with increasing moisture content in inlet air and the concentration of inlet solution. The humidification rate increased substantially but the humidification efficiency decreased as the inlet air flow rate increased. The error between the simulations and experimental results is acceptable, meaning that our model can provide a theoretical basis for optimizing the performance of a humidifying evaporator.
Key words: heat pump; condensation heat; discrete phase model (DPM); liquid desiccant evaporator; numerical simulation
Cite this article as: NIU Run-ping, CHEN Xiao-yi, WANG Zi-ye, KUANG Da-qing. Numerical simulation of liquid desiccant evaporator driven by heat pump [J]. Journal of Central South University, 2019, 26(8): 2197-2213. DOI: https://doi.org/10.1007/s11771-019-4166-8.
1 Introduction
Air humidity and temperature both affect the indoor environment of living, working, and industrial production spaces. Winter and spring in areas of temperate continental climate (such as northern China) are the driest seasons of the year. The use of air conditioning and heating equipment can cause the indoor air to be even drier, creating an environment that can easily cause illness and affect human health [1]. Most indoor air conditioners currently in use are vapor-compression-type air conditioners. In winter, vapor-compression air conditioners cannot humidify indoor air. Vapor- compression air conditioning uses condensation dehumidification, and the surface moistened by the condensed water can easily harbor bacteria. Conventional air conditioners control air humidity by freezing dehumidification to regulate the dew point temperature of the air. They then reheat the air after dehumidification according to the relative humidity required [2]. Conventional air- conditioning systems sacrifice the control of humidity to better control temperature. Reheating air after cooling and dehumidification results in unnecessary energy consumption [3]. An air- conditioning system that can ensure the regulation of indoor humidity as well as temperature would benefit the environment through energy savings and significantly improve the quality of life in northern China.
Liquid-desiccant air conditioning systems have the potential to meet the above requirements. These systems have many advantages such as the ability to use low-grade energy, low energy consumption, and environmental protection among others [4-7]. The principle of heating and humidifying air in winter is the same as in summer. An external heat source is used to heat the solution until its temperature and water vapor pressure are higher than those of the air. After a series of heat and mass transfer operations, the solution is concentrated and regenerated, and the air is heated and humidified [8]. In summer, dilute solution is concentrated and regenerated to obtain a higher concentration solution for air dehumidification.
There is a substantial body of research on dehumidification and regeneration technology. ZENG et al [9] developed a heat-pump-driven dehumidification air conditioning system to carry out an experimental study on the regeneration of low-concentration LiCl solution using condensation heat. They found that increasing the flow rates and temperatures of the air solution increases the regeneration volume. LIU et al [10] simulated and conducted experiments on cross-flow regenerators using lithium bromide solution. Their calculated total thermal efficiency and regeneration efficiency differed from the experimental results by less than 15%, suggesting that their numerical model is accurate and reliable. WANG [11] studied the effect of solution and air inlet parameters on LiCl solution regeneration using a countercurrent packed column. ZHOU et al [12] studied three regeneration methods: solar photothermal regeneration, solar photovoltaic regeneration, and solar photovoltaic/ thermal (PV/T) regeneration. Their simulations showed that the concentration difference between the regenerator inlet and outlet was the greatest for LiBr solution, while the LiCl solution had the strongest dehumidifying effect after regeneration. LI et al [13] set up an experimental platform for regenerating the solution by boiling at low pressure and developed a mathematical model to analyze the effects of different operating conditions on the performance of the solution regeneration device. HUANG et al [14] developed a mathematical model to simulate the heat and mass transfer processes and solution regeneration in a crossflow solution regenerator. Their simulations results are basically consistent with the experimental results and the deviation is less than 5%, which proves that their heat and mass transfer model is reliable.
The research described above mainly applies to dehumidifying air in summer by regenerating the dehumidification solution, but there is little research on the heating and humidification of air by the solution in winter. LIU et al [15] reported that a fresh air unit with full heat recovery has a coefficient of performance in winter that is high enough to solve the problem of fresh air heating and humidification. KE et al [16] set up a liquid- desiccant fresh air unit driven by a heat pump and studied its heating and humidifying performance under winter working conditions. They found that the heating and humidifying performance of the fresh air unit increased with the temperature of the inlet solution but worsened as the concentration of the solution increased. NIU et al [17] developed a solution humidification air conditioning system and tested it under winter working conditions. They found that increasing the solution mass flow and the temperature and moisture content of the inlet air improved the performance of the liquid-desiccant air-conditioning system.
In this work, we used the discrete phase model (DPM) in the FLUENT software package to simulate the heat and mass transfer in a liquid- desiccant evaporator and determine the influence of the inlet solution and air parameters on the heating and humidifying performance of the evaporator under winter conditions. We compared the simulation results with experimental results to ensure the accuracy of the simulation. We also characterized the humidification performance of the liquid-desiccant evaporator using the humidification capacity and humidification efficiency as indexes, and provide a theoretical basis for the optimal design of the liquid desiccant evaporator.
2 Liquid-desiccant evaporator
2.1 Experimental setup
A heat pump driven liquid-desiccant air conditioning system was developed for this study. This system couples the evaporator and condenser of a traditional compression refrigeration system with the dehumidifier and regenerator of a liquid-desiccant air conditioning system. The dehumidifier and evaporator are in the form of an evaporative condenser.
A four-way reversing valve is used to convert the dehumidifier evaporator used for summer operation into the heating and humidifying device for winter operation. When the system is running in winter, fresh air is heated and humidified in the liquid-desiccant evaporator. The main components of the liquid-desiccant evaporator are a fan, a water collector, a sprinkling device, a circulating pump, a heat transfer coil, and a water tank. A schematic diagram of the structure of liquid desiccant evaporator is shown in Figure 1.
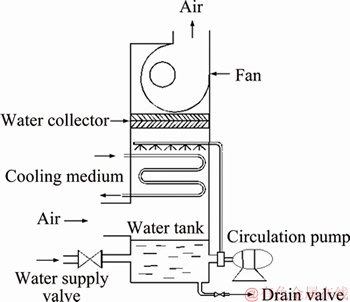
Figure 1 Schematic diagram of humidifying evaporator structure
2.2 Working principles
The mixed system consisting of the liquid desiccant system and the heat-pump-driven compression refrigeration system is more complex. In the refrigerant circulation process under winter conditions, the refrigerant is compressed by the compressor into high-temperature and high- pressure superheated refrigerant vapor that is then sent to the coil pipe of the liquid desiccant evaporator (condenser) for indirect heat transfer to the solution and air outside the pipe. The heat in the refrigerant is discharged to heat and evaporate the solution, and the refrigerant is then transformed into a high-temperature and high-pressure liquid that enters the heat transfer coil of the regenerative evaporative condenser (evaporator) and absorbs heat from the solution and air outside the wall of the pipe. This cycle completes the humidification process of the liquid-desiccant evaporator under winter conditions.
During winter operation, the regenerative evaporative condenser is converted into an endothermic component using a four-way reversing valve. The liquid desiccant evaporator is used as the heat-releasing component for heating and humidifying indoor air. When the condenser becomes an evaporator, solution is sprayed to prevent the evaporator from frosting. Lithium chloride solution, because of its low crystallization temperature, can be used for air treatment in low-temperature environments and to prevent instability in the heat supply caused by outdoor frost.
3 Numerical simulation
3.1 Mathematical model
A 1:1 numerical model of the whole liquid- desiccant evaporator was developed using FLUENT soft ware, and discrete phase numerical simulations were carried out. The pipe wall temperature was set to a fixed value of 35°C because condensation heat was used as the heat source. The multiphase flow model was used for numerical simulation, and the internal flow field of the equipment under specific operating conditions was obtained.
The main multiphase flow models in Fluent are the VOF model, the mixture model, the Euler model, and the DPM model [18, 19]. The VOF, mixture, and Euler models are all continuous models. The VOF model is suitable for the calculation of layered flow and free surface flow, while the mixture model and the Euler model are more suitable for flow problems with volume concentrations higher than 10%. The DPM model is a discrete phase model that tracks the trajectory of particles in the flow field and selects whether the coupling between continuous phase and discrete phase can be carried out. To solve the multiphase flow model, the continuous phase is calculated by solving the governing equations of the flow field, and the trajectory of particles in the flow field is calculated using the discrete phase model [20]. Because of the complex heat and mass transfer process between the air and the solution in the solution humidification evaporator, the DPM model was chosen to model the humidification evaporator by coupling the continuous phase with the discrete phase.
The Euler method was used to solve the Navier-Stokes equations for the flow field of continuous phase gas. Discrete phase flow field parameters are used to calculate the trajectory of droplet particles by the Lagrangian method [21].
Continuous phase equation: The equations for modeling the continuous phase include the mass, momentum, and energy conservation equations.
Mass conservation equation:
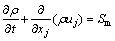 (1)
(1)
where Sm is any custom source term that is part of the mass of a continuous phase.
Momentum conservation equation:
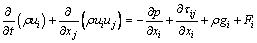 (2)
(2)
where Fi contains related source items; τij is the stress tensor; and P represents pressure.
Turbulence model: standard k-ε model [22].
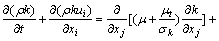
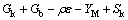 (3)
(3)
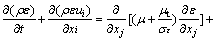
 (4)
(4)
where Gk and Gb represent the production of turbulent kinetic energy, caused by the average velocity gradient and Buoyancy force; YM is caused by pulsation and expansion in compressible turbulence; C1ε, C2ε and C3ε are empirical constants; σk and σε correspond to the turbulent kinetic energy and the dissipation rate, respectively; and Sk and Sε are user-defined source items.
Component conservation equation: For the solution of component transport processes that do not involve chemical reactions, an unresponsive component transport model can be used. This model can be solved for the spatial-temporal distribution of each component in the process of convection and diffusion based on the law of conservation of mass for each component.
 (5)
(5)
where cs is the component mass fraction; ρcs is the mass concentration of the component; and Ds is the diffusion coefficient of the component.
Discrete phase equation: The discrete phase consists of spherical droplets distributed in the air that constitutes the continuous phase. The flow in the discrete phase was calculated by the Lagrange method to obtain the droplet velocity, motion trajectory, and other quantities. The continuous and discrete phases influence each other, and their coupling interaction was also calculated. The droplet particles were assumed to be ideal spheres, and the volume fraction of the particle phase was generally kept below 10%. With no interaction, no collision, and no aggregation between particles, the particle trajectories were calculated for a single particle. By solving the droplet trajectory equation and other auxiliary equations, the position and velocity of the droplet at any time were obtained [23].
The trajectories of droplets affected by turbulent air were calculated using the stochastic droplet tracing method, with the air velocity selected randomly from a Gaussian distribution. The velocity of liquid droplet movement in LiCl solution was obtained by analyzing the force between the air and the fluid. The droplet trajectory equation can be expressed as follows:
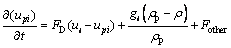 (6)
(6)
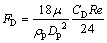 (7)
(7)
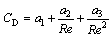 (8)
(8)
where ui is the continuous phase velocity; upi is the droplet velocity; μ is the molecular viscosity of the fluid; ρ is the continuous phase density; ρp is the droplet density; Dp is the droplet diameter; Re is the Reynolds number of the droplets; Fother is an additional acceleration (force/unit particle mass) term; FD is the drag force per unit particle mass; and a1, a2 and a3 are constants that apply to smooth spherical droplets [24].
Mass consumption:
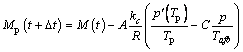 (9)
(9)
Heat balance: The evaporation of droplets is affected by two main factors: the vapor on the surface of the droplet and the vapor pressure on the air surface. The pressure gradient between the two factors determines the diffusion rate of the droplet into the gas phase.
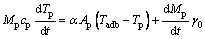 (10)
(10)
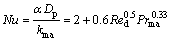 (11)
(11)
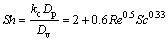 (12)
(12)
where α is the droplet surface heat transfer coefficient, W/(m2·K); kma is the thermal conductivity of the air, W/(m2·K); Nu is the Nusselt number; Pr is the Prandtl number; Dv is the binary diffusion rate of solution vapor, m2/s; Sh is the Sherwood number; Sc is the Schmidt number.
The heat and mass transfer and kinetic energy of a particle may change during its trajectory, but the initial values of the parameters governing the interaction with the continuous phase were used in the calculations on the continuous phase to determine the coupling and interaction between the two phases.
Mass equation:
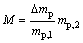 (13)
(13)
Energy equation:
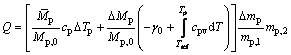 (14)
(14)
Momentum equation:
 (15)
(15)
where Δmp is the quality change of solution droplets in the body, kg; mp,1 is the mass of initial solution droplets, kg; mp,2 is mass flow at nozzle outlet, kg/s; 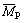 is the average droplet mass in the body, kg; ΔTp is the temperature change of solution droplets in the body, K; Cpv is the specific heat capacity of solution vapor, J/(kg·K); Tp is the temperature in K at which the solution droplets flow out of the control body.
is the average droplet mass in the body, kg; ΔTp is the temperature change of solution droplets in the body, K; Cpv is the specific heat capacity of solution vapor, J/(kg·K); Tp is the temperature in K at which the solution droplets flow out of the control body.
The continuous phase is air, and the discrete phase is composed of spherical droplets distributed in the continuous phase. The discrete phase calculation was done using the coupling discrete phase solution method, and the default SIMPLE algorithm in Fluent was used to solve the control equation. Momentum interpolation calculations used the second order upwind scheme, and turbulence characteristics were calculated using a first order upwind interpolation scheme [25].
3.2 Description of simulated geometry
A 1:1 simplified three-dimensional model of a working liquid-desiccant evaporator was created using the Fluent software package. As shown in Figure 2(a), the dimensions of the model were 495 mm×495 mm×700 mm. The nozzle was 200 mm from the first row of bundles and directed downward. The heat transfer coil was constructed of a snake-shaped pipe with a diameter of 16 mm and a transverse spacing of 35 mm. It was arranged in a forked row at an angle of 60° with nine pipes in the first rows and ten pipes in the second rows. Two sides of the bottom of the box had grid inlets at an angle of 150° from vertical. The height of the inlet grid was 150 mm, and the distance from the bottom end was 70 mm. The actual equipment was completely symmetrical, so only half the actual evaporator was modeled to shorten the computation time while maintaining the accuracy of the analysis. In previous work on the discretization of each grid, mesh generation was performed to divide the continuous space into finite meshes. The meshing method plays a decisive role in the quality of the meshes, which affects the results and accuracy of subsequent simulations [26]. We used the meshing module of Workbench to perform unstructured meshing of the computational area of the model. The whole mesh was generated automatically with local mesh refined around the coil specifically. The total number of mesh points was 5.919 million. A schematic of the model after meshing is shown in Figure 2(b).
The model jet source and boundary conditions were then set. The jet source of the model was a solid-cone nozzle with spray at the top center of the box (the highest point on the y axis). The droplet was sprayed downward in the y-direction using a random orbit model. The spray angle was 100°, the number of particles in the spray was 200, and the number of continuous phase iterations per DPM was 300 [27]. The initial velocity of the droplet was 2 m/s, the internal diameter of the nozzle was 15 mm, and the average diameter of the spray droplet was 0.5 mm. The material parameters of the spray liquid including temperature, flow rate, density, specific heat, latent heat, vaporization temperature, etc., were assigned based on the simulation parameters.
Figure 2 Numerical simulation model:
A symmetric boundary condition was used at the symmetrical interface. The outer layer of the inlet window was an air inlet, which was set as a velocity inlet. The air outlet at the top of the equipment was set as a pressure outlet (standard atmospheric pressure). The middle pipe bundle area and the box body were wall surfaces. The pipe bundle area material was set to carbon steel, and the default no-slip wall boundary condition was chosen.
An adiabatic boundary condition was applied around the model, and the thickness of the pipe wall was ignored. The contact coil of droplet flow and the surrounding wall were reflective, the tangential coefficient was 1, and the normal direction was 0.1.
In the process of numerical simulation, the relaxation factor for the energy equation was set to 0.8, and the default values were used for the other parameters. The calculation converged when the residual z-velocity was less than or equal to ×10-3 or the amount of each index satisfying any point in the calculation domain became stable.
4 Results and discussion
The flow field distribution in the solution regenerator was analyzed under a set of reference operating conditions. We then studied how changes in the operating parameters affected the outlet air and solution parameters and the humidification performance. Table 1 shows the range of inlet parameters selected for simulation. The inlet air speed was derived from the inlet air volume and the rest of the spray solution parameters are described in Section 3.2.
4.1 Spatial distribution analysis
We analyzed the xy plane at z=247.5, the yz plane at x=247.5, and the distribution of air outlet surface and spray droplets.
1) Distribution of velocity, pressure, temperature, and moisture content on xy surface at z=247.5
Figure 3(a) shows that the velocity of air was higher under the pipe bundle and that there was a partial eddy current near the wall of the box. The air velocity at the center of the eddy current was higher than in the surrounding area. Figure 3(b) shows that the total air pressure decreased gradually from the bottom to the top, and was higher under the pipe bundle and that the transverse pressure distribution decreased gradually from center to outside, being higher at the outlet than at the outer side because of the dense spray droplets at the center. Figure 3(c) shows that the air temperature increased because the air absorbed heat from the wall of the pipe bundle. The temperature of the air in the central part of the pipe bundle area was lower than that on both sides. This was because the temperature of the spray solution here was 17 °C, which was significantly lower than the temperature of the pipe wall (40 °C). Figure 3(d) indicates that the moisture content distribution was generally higher in the middle section of the pipe bundle, while the moisture content near the air outlet of the tank was higher than in the central portion. This was caused by the spray droplets being more densely distributed near the center, where the greater contact between the air and the droplets increased the mass transfer between them.
Table 1 Range of simulated parameters

2) Distribution of velocity, pressure, temperature, moisture content on symmetric yz surface at x=247.5
Figure 4(a) indicates that the velocity of air was the highest when it passed through the inlet grid. The fluid velocity was the highest above the water tank, and gradually decreased from the bottom of the box to the top. The total air pressure field distribution in Figure 4(b) shows that the pressure was the highest at the inlet window. As the air slowly enters the tank, the pressure distribution in the tank is even. Figure 4(c) shows that the air temperature near the pipe wall was also high. This occurred because the air formed a high-speed flow around the coil gap that enhanced the heat and mass transfer between the water droplets and the air. The air temperature in the upper central part of the bundle was lower than the temperature of the two sides.
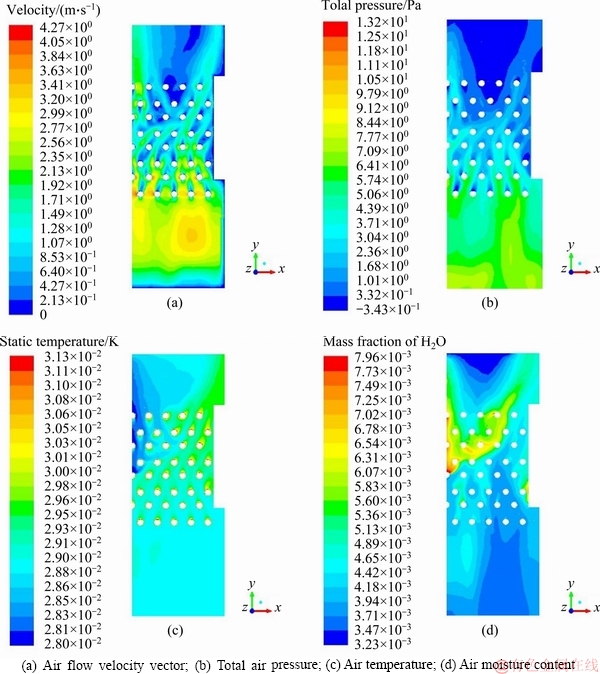
Figure 3 Simulated nephogram with different parameters on xy surface:
Figure 4(d) shows that the highest moisture content occurred in the upper central part of the bundle and in the vortex area below the bundle, where the droplets were dense and the mass transfer between the air and droplets was more efficient. Water vapor accumulated and moisture content increased because of a vortex, which indicated that latent heat transfer was more intense. The moisture content near the air outlet at both sides of the box was higher than that in the central part.
3) Distribution map of air velocity, pressure, temperature and moisture content at outlet
Figure 5 shows that the distributions of velocity, temperature, and moisture content at the air outlet were consistent with those at the outlet of z (247.5) and the symmetric plane. More specifically, the velocity distribution vector graph in Figure5(a) shows that the overall distribution was relatively uniform. However, an increase in velocity from the outside to the inside was observed, resulting in a higher velocity at the innermost parts of the region. The air velocity at the upper and lower sides of the exit (i.e. the direction of the x axis) was higher than in the z direction. This was mainly caused by the air grid inlet shown in the upper and lower edges of the figure (i.e., in the x-direction). Figure 5(b) indicates that the air pressure decreased gradually inwards: the external pressure was higher than the interior pressure, and the innermost pressure was the lowest. Figure 5(c) shows that the air temperature gradually decreased from outside to inside. The moisture content distribution of the air in Figure 5(c) decreased from the outside to the inside, and the air moisture content on both sides of the outlet was higher than in the z-direction.
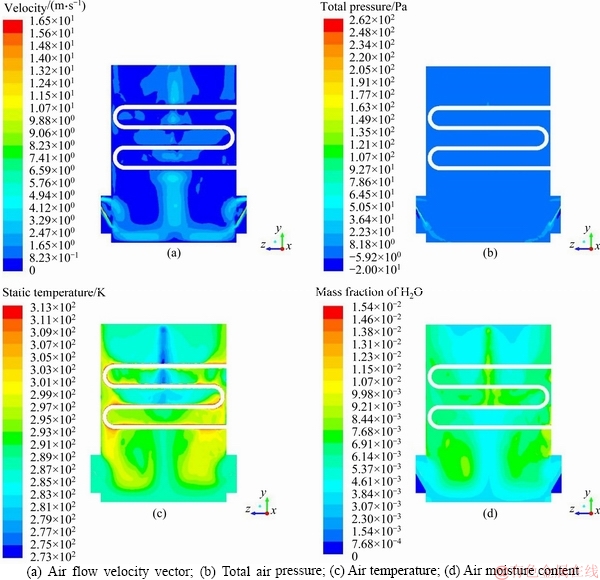
Figure 4 Simulated nephogram with different parameters on yz surface:
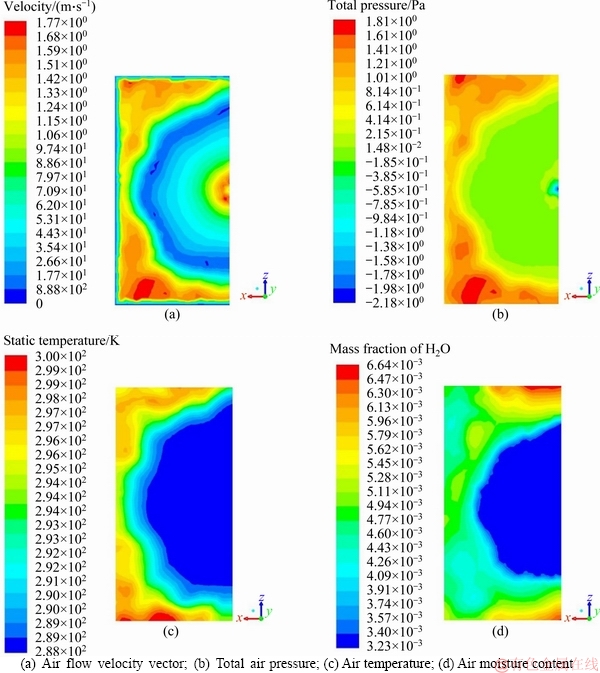
Figure 5 Simulated nephogram with different parameters on outlet surface:
4) Velocity, temperature and mass distribution of spray solution
Figure 6 shows the changes in spray properties after the droplets were ejected from the nozzle. The spray had a typical conical distribution and did not reach the pipe bundle area. The direction of droplet motion depended on its initial position. After reaching the pipe bundle area, the air flowed in a crossed manner, and collided and was reflected by the pipe bundle. The distribution was relatively disordered.
The droplet velocity field distribution diagram in Figure 6(a) shows that the droplet velocity increased gradually from the top to the bottom, and that there were obvious changes in direction and velocity at the coil pipe and pipe wall. The change in velocity affected the intensity and depth of heat and mass transfer between the droplets, the air, and the pipe wall. Figure 6(b) indicates that with the droplets moving from the top to the bottom, the temperature changed gradually. Heat absorption was strongest in the upper part of the box and decreased from the top to the bottom, dropping particularly sharply at the air inlet. The temperature of the droplets decreased after passing through the vent due to heat and mass transfer with the lower- temperature air at the inlet. The higher-temperature droplets transmitted sensible and latent heat to the air, causing their temperature to drop rapidly. The droplet mass distribution in Figure 6(c) shows that the droplet mass decreased gradually from the top to the bottom, which indicates that the effect of the solution on latent heat transfer between the air and the solution was increasing.
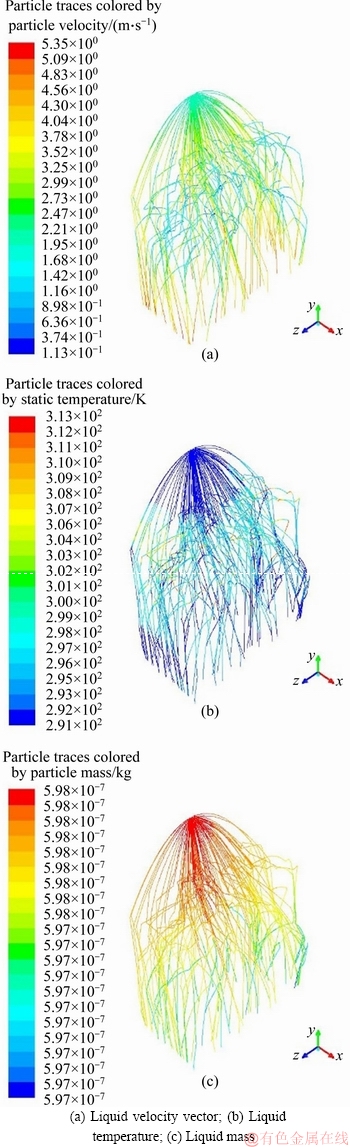
Figure 6 Simulated nephogram with different parameters of spray solution:
4.2 Univariate analysis
4.2.1 Inlet air mass flow rate
Figure 7 shows the outlet parameters, humidification capacity, and humidification efficiency of the solution and air as a function of the inlet air mass flow. Figure 7(a) indicates that the air temperature and outlet air moisture content decreased as air flow increased. Figure 7(b) shows that the temperature of outlet solution decreased, while the outlet solution concentration increased with increased air flow rate. Figure 7(c) shows that increased air mass flow increased humidification capacity but decreased humidification efficiency.
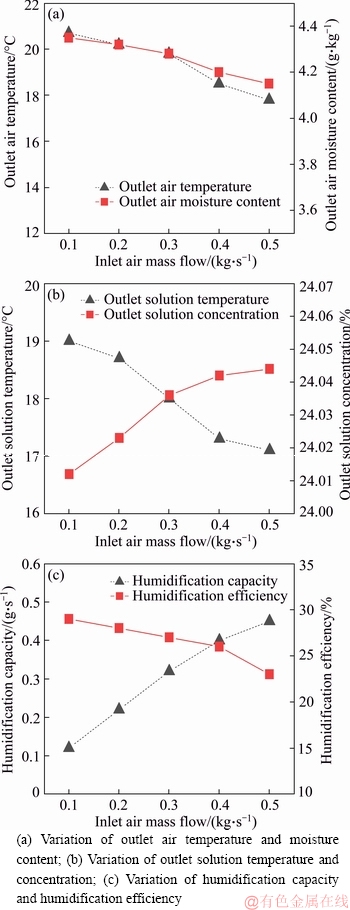
Figure 7 Influence of inlet air mass flow:
4.2.2 Mass flow of inlet solution
Figure 8 shows that the outlet air temperature,moisture content, solution temperature, solution concentration, humidification capacity, and humidification efficiency increased as the solution flow rate increased. This behavior was observed in both simulations and experiments. Because the simulated droplet particles were sprayed with random orbits, the distribution of particles between pipes cannot be perfectly uniform. Figure 8(b) indicates that the outlet temperature of the solution was a smooth rising curve, and that the experimental data did not first increase and then decrease. As the flow rate of spray solution increased, the heat transfer between the solution and the pipe wall increased, and the solution temperature also increased. Figure 8(a) shows that the moisture content of the air outlet increased with increasing solution flow rate.
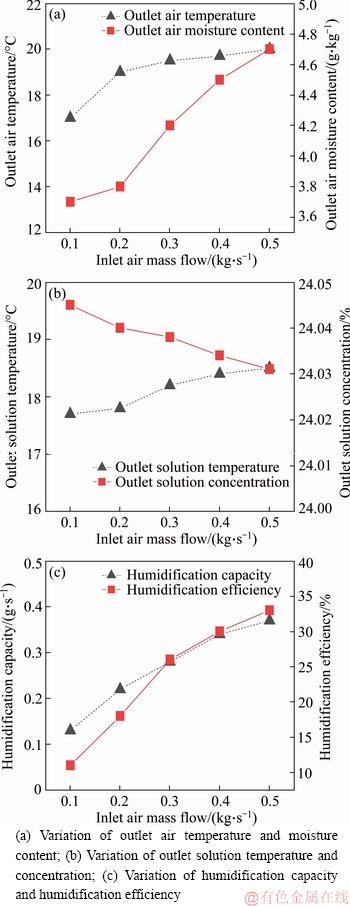
Figure 8 Influence of inlet solution mass flow:
4.2.3 Inlet air temperature
Figures 9(a) to (c) show that for both simulations and experiments, the outlet air temperature, moisture content, solution temperature, solution concentration, humidification capacity, and humidification efficiency increased as the inlet air temperature increased. The simulation showed a slow increase, indicating that increasing the inlet air temperature has a low impact on the humidification performance of the system. If the inlet air temperature were higher than the solution temperature, the air could transfer heat to the solution, leading to better humidification performance.
4.2.4 Inlet air moisture content
Figure 10 shows that the outlet air temperature, moisture content, solution temperature and solution concentration increased with the inlet air moisture content. Figure 10(c) shows that the humidification capacity and humidification efficiency decreased with increasing inlet air moisture content. As the moisture content of the inlet air increases, the decrease in humidification efficiency became larger. However, this unfavorable trend slowed down when moisture content became higher.
4.2.5 Temperature of inlet solution
Figure 11 shows that the outlet air temperature, moisture content, solution temperature, and solution concentration increased with the inlet solution temperature, while the humidification capacity and humidification efficiency decreased as the inlet solution temperature increased. The simulation results from Figures 11(a) and (c) indicate that the heating and humidifying performance of the system can be improved by raising the temperature of the inlet solution.
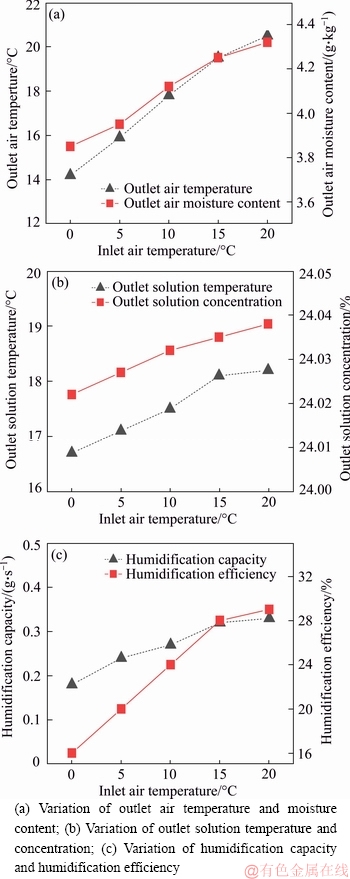
Figure 9 Influence of inlet air temperature:
4.2.6 Concentration of inlet solution
Figures 12 (a) and (b) show that the outlet air temperature and the solution concentration increased with increasing inlet solution concentration. Figures 12 (a) and (c) show that the moisture content, humidification capacity, and humidification efficiency of the system decreased as the inlet solution concentration increased.

Figure 10 Influence of inlet air moisture content:
Table 2 shows a comparison of simulated water and 21% lithium chloride solution outlet parameters. The temperature of the outlet solution was lower when the spray solution was water rather than lithium chloride solution. However, the humidification efficiency of the water was lower than that of the lithium chloride solution. This was mainly due to the fact that the equivalent moisture content of water was relatively large.
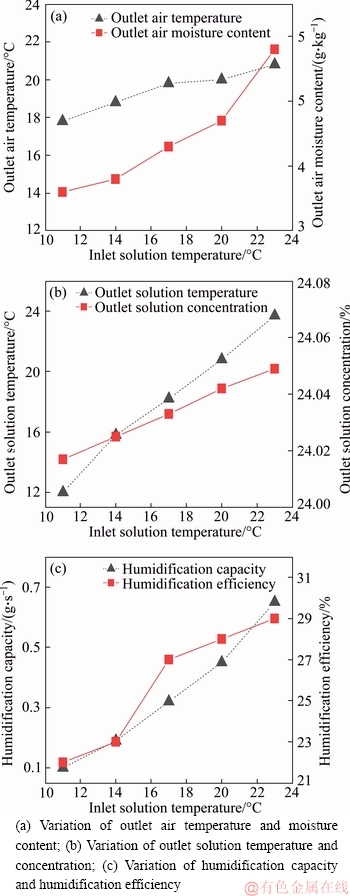
Figure 11 Influence of inlet solution temperature:
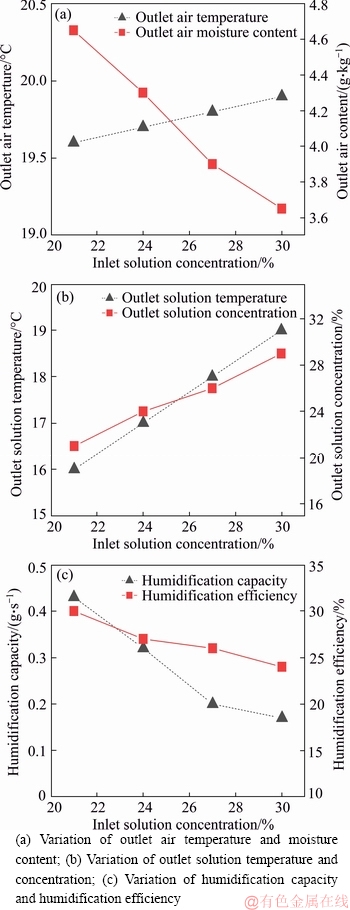
Figure 12 Influence of inlet solution concentration:
Table 2 Comparison of exit parameters between lithium chloride solution and water

4.2.7 Pipe wall temperature
Figure 13 shows that the outlet air temperature, moisture content, solution temperature, solution concentration, humidification capacity, and humidification efficiency increased as the pipe temperature increased. At a constant air flow rate, the humidification increases with the pipe wall temperature because of the greater difference in moisture content between the air inlet and outlet. The outlet concentration of the solution may also increase with the wall temperature because of the constant flow rate of the solution and the increase in the humidification capacity.
Figure 13(c) shows that the humidification efficiency increased from 6.81% to 87.44% when the pipe wall temperature increased from 30 °C to 50 °C. Increasing the pipe wall temperature increases the condensation heat of the system, which further increases the refrigerating capacity. In addition, improving the coefficient of performance of evaporator and condenser in a heat pump system is beneficial to improve the humidification performance of the system.
5 Simulation and experiment comparison
We verified the accuracy and applicability of the model by comparing the simulation results with reliable experimental data.
As shown in Figure 14, the error in the simulation outlet air temperature was relatively larger than the errors in other quantities. The maximum error in the outlet air temperature was 14.68%, while the errors in moisture content of outlet air, solution temperature, and solution concentration error were within ±10%. The causes of the errors are as follows:
1) The simulated results were the averaged values of the parameters of the outlet air interface and the liquid droplets. In the experiments, the location of the instrument for collecting the exit parameters was slightly different from the outlet position of the model.
2) The influence of the upper nozzle demister, the pressure drop of the flow field, and the temperature was not taken into account in the model. Limitations in the fluent software meant that the nozzle had to be treated as solid, rather than the spiral nozzle used in practice.
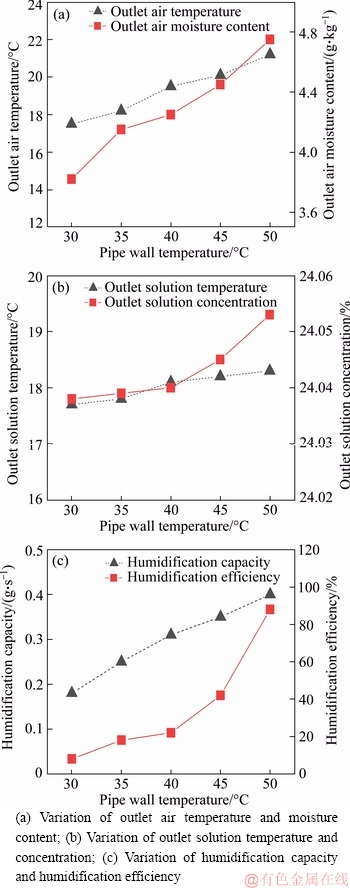
Figure 13 Influence of pipe wall temperature:
3) In the numerical simulation, the setting of particle boundary conditions and the selection of parameters for the behavior of droplet particles touching the wall make part of the air directly contact with the pipe wall to transfer heat. The uniformity of the droplet spray and the wetting degree of the heating surface in the numerical simulations were slightly different from those in the experiment tests.

Figure 14 Comparisons between simulation results and experimental results:
6 Conclusions
In this work, the standard turbulence model and discrete phase model (DPM) in the FLUENT software package were used to simulate the heat and mass transfer in a humidification evaporator and obtain the velocity and temperature fields in the device. The numerical simulation results provide a theoretical basis for predicting and optimizing the performance of the equipment. The main results are summarized below.
1) The influence of factors such as the inlet air temperature and moisture content was studied through simulation. The simulated values of the temperature of the outlet air, the temperature of the outlet solution, and the humidification increased slowly compared with the experimental values. This indicated that the higher the inlet air temperature, the better the humidification performance of the system. The higher the inlet air moisture content, the worse the humidification performance of the system.
2) When the pipe wall temperature increased from 30 °C to 50 °C, the humidification efficiency increased from 6.81% to 87.44%. Improving the coefficient of performance of evaporator and condenser in a heat pump system is beneficial to improve the heating and humidification performance of the system.
3) The error in the predicted outlet air temperature was less than 15%, and the errors in outlet air moisture content and solution temperature were within 10%.
4) The numerical model that we have developed can predict the performance of the equipment under various operating conditions and is suitable for research on this kind of equipment. It can be used to achieve the performance prediction of the humidifying evaporator, which has great benefit in saving money and improving the analysis accuracy.
Nomenclature
A
Surface area, m3
a1, a2, a3
Constants in drag coefficient calculation
C1ε, C2ε, C3ε
Empirical constants
Cs
Volume concentration of component s
Ds
Diffusion coefficient of component s
Dp
Droplet diameter
Dv
Binary diffusion rate of solution vapor, m2/s
FD
Drag force per unit mass, m/s2
Fother
Other forces
Fi
Contains related source items for other models
Gk
Turbulent kinetic energy caused by average velocity gradient
Gb
Turbulent kinetic energy caused by buoyancy
kma
Thermal conductivity of the air, W/(m2·K)
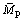
Average mass of droplets, kg
mp,0
Initial mass of droplets, kg
p
Pressure, Pa
Nu
Nusselt number
Pr
Prandtl number
Re
Reynolds number
Sm
Custom source item
Sh
Sherwood number
Sc
Schmidt number
ΔTp
Droplet temperature leaving the control body, K
ui
Air velocity, m/s
upi
Droplet velocity, m/s
Greek symbols
τij
Stress tensor
ρ
Density, kg/m3
μ
Aerodynamic viscosity, Pa·s
α
Droplet surface heat transfer coefficient, W/(m2·K)
Abbreviation
LiBr
Lithium bromide
LiCl
Lithium chloride
DPM
Discrete phase model
VOF
Volume of fluid
References
[1] JIANG Yi, LI Zhen, CHEN Xiao-yang, LIU Xiao-hua. Liquid dehumidification air conditioning system and its application [J]. HVAC, 2004, 34(11): 88-96. (in Chinese)
[2] LI Yuan-xi, HUANG He, YANG Yong-feng, TU Ai-min. Performance experiment of plate evaporative condenser [J]. Refrigeration and Air-Conditioning, 2011, 11(4): 43-48. (in Chinese)
[3] DING Yun-fei, DING Jing, YANG Xiao-xi. Liquid desiccant cooling air-conditioning system and its progress [J]. Fluid Machinery, 2004, 32(6): 43-47. (in Chinese)
[4] SU Wei, ZHANG Xiao-song. Thermodynamic analysis of a compression absorption refrigeration air-conditioning system coupled with liquid desiccant dehumidification [J]. Applied Thermal Engineering, 2017, 115( 25): 575-585.
[5] WANG Ling-shi, XIAO Fu, ZHANG Xue-jun. An experimental study on the dehumidification performance of a counter flow liquid desiccant dehumidifier [J]. International Journal of Refrigeration, 2016, 70(10) : 289-301.
[6] ELHELW M. Performance evaluation for solar liquid desiccant air dehumidification system [J]. Alexandria Engineering Journal, 2016, 55(2): 933-940.
[7] ZHANG Lun, LIU Xiao-hua, JIANG Jing-jing, JIANG Yi. Energy calculation and analysis of a dehumidification system using liquid desiccant [J]. Energy and Buildings, 2014, 69(2): 318-328.
[8] CHANG Xiao-min, LIU Xiao-hua, XIE Xiao-yun, JIANG Yi. Winter performance analysis on a liquid desiccant fresh air handling unit driven by heat source [J]. HVAC, 2007, 37(12): 106-110. (in Chinese)
[9] ZENG Tai-ye, ZHANG Xiao-song, CHEN Yao. Experimental investigation for low-concentration liquid desiccant regeneration with utilization of condensation heat [J]. Journal of Refrigeration, 2018, 39(1): 76-82. (in Chinese)
[10] LIU Xiao-hua, JIANG Yi, CHANG Xiao-min, YI Xiao-qin. Heat and mass transfer performance analysis of cross-flow regenerators in a liquid desiccant air conditioning system [J]. HVAC, 2005, 35(12): 10-15. (in Chinese)
[11] WANG Min. Study on the performance of regenerator for liquid desiccant air Conditioning system [D]. Tianjin: Tianjin University of commerce, 2014. (in Chinese)
[12] ZHOU Jun-ming, ZHANG Xiao-song, SUN Bo. Solar liquid dehumidification air conditioning system regeneration technology and energy analysis research progress [J]. Journal of Refrigeration, 2019, 40(2): 154-160. (in Chinese)
[13] LI Da, LIANG Cai-hua, JIANG Dong-hai. Research on performance of heat source tower heat pump low pressure boiling liquid regeneration device [J]. Chinese Journal of Refrigeration, 2017, 37(2): 25-31. (in Chinese)
[14] HUANG Zhi-jia, LI Yao-guo, YIN yan-yan. Numerical simulsation of heat and mass transfer Process in liquid regenerator [J]. Journal of Chemical Industry and Engineering, 2008, 59(2): 159-162. (in Chinese)
[15] LIU Xiao-hua, LI Zhen, JIANG Yi. Liquid desiccant total heat exchanger and heatpump combined fresh air handling units [J]. HVAC, 2004, 34(11): 98-102. (in Chinese)
[16] KE Rui, HUANG Zhi-jia, LUO Liang, et al. experimental study on winter performance of liquid desiccant fresh air handling unit driven by heat pump [J]. Refrigeration and Air-Conditioning, 2018, 18(9): 42-46. (in Chinese)
[17] NIU Run-ping, MENG Fu-qiang, WANG Zi-ye, WANG Shi-zheng. Analysis of influence factors on humidification characteristics of liquid desiccant air-conditioning system in winter [J]. Journal of Shenyang Jianzhu University (Natural Science), 2018, 34(3): 543-549. (in Chinese)
[18] JIANG Fan, HUANG Peng. fluent advanced application and case analysis [M]. Beijing: Tsinghua University Press, 2007: 167-196. (in Chinese)
[19] YU Yong, ZHANG Jun-ming. Introduction to fluent and advanced tutorials [M]. Beijing: Beijing Institute of Technology Publishing House, 2008: 167-196. (in Chinese)
[20] ZHANG Tan. Experimental study and simulation on performance of solar liquid desiccant regenerator [D]. Inner Mongolia University of Science & Technology, 2015. (in Chinese)
[21] TIAN Fu-jun. The principle and application of CFD software for fluid computional dynamics analysis [M]. Beijing: Tsinghua University press, 2004: 16-23. (in Chinese)
[22] ZHANG Fu-ren, ZHANG Hui, ZHUANG Chun-long. CFD numerical simulation of dispersion law of indoor gas leakage based on weather conditions [J]. Journal of Central South University of Technology, 2009, 16(s1): 62-67.
[23] KARAGOZ I, KAYA F. CFD Investigation of the flow and heat transfer characteristics in a tangential inlet cyclone [J]. International Communications in Heat and Mass Transfer, 2007, 34: 1119-1126.
[24] WANG Wei-fan. Numerical simulation of mechanical ventilation crossflow cooling tower [D]. Ji'nan: Shandong University, 2007. (in Chinese)
[25] MORSI S A, ALEXANDER A J. An investigation of particle trajectories in two-phase flow systems [J]. Fluid Mech, 1972, 55(2): 193-208.
[26] WANG Ling-yun, HUANG Hong-hui, RAE W. West. Impeller modeling and analysis based on UG NX/KF and Fluent [J]. Journal of Central South University, 2012, 19: 3430-3434.
[27] WAN Fang-fang. Numerical simulation and optimization of evaporative condenser [D]. Zhengzhou: Zhengzhou University, 2010. (in Chinese)
(Edited by YANG Hua)
中文导读
热泵驱动调湿式蒸发器的数值模拟
摘要:对冬季工况下热泵驱动的调湿式蒸发器加湿性能进行研究。采用标准k-ε湍流模型和离散相模型,利用FLUENT软件对热泵驱动的溶液调湿式蒸发器的传热传质过程进行数值模拟,得到装置内的温度场和速度场等分布。分别对进口溶液浓度(21%,30%)和管壁温度(30 °C,50 °C)等情况下的调湿式蒸发器性能进行了研究。研究结果表明,随着进口空气温度、溶液流量、溶液温度和管壁温度的升高,加湿量和加湿效率均增大;随着进口空气含湿量和进口溶液浓度的升高,加湿量和加湿效率均减小;随着进口空气流量的升高,加湿量增大但加湿效率降低。将模拟与实验结果进行对比分析,误差在允许范围内,数值模型为调湿式蒸发器的性能优化提供了理论依据。
关键词:热泵;冷凝热;离散相模型(DPM); 调湿式蒸发器;数值模拟
Foundation item: Project(2016YFC0700100) supported by the National Key R&D Program of China; Project(JDJQ20160103) supported by Promotion of the Connotation Development Quota Project of Colleges and Universities-Outstanding Youth of Architectural University, China
Received date: 2019-04-29; Accepted date: 2019-07-17
Corresponding author: NIU Run-ping, PhD, Associate Professor; Tel: +86-13911607350; E-mail: niurunping@bucea.edu.cn; ORCID: 0000-0002-6512-2784

