模糊故障Petri网建模方法及其应用

黄敏，林啸，侯志文

(长沙理工大学 计算机与通信工程学院，湖南 长沙，410014)

摘要：为克服模糊Petri网和故障Petri网在模拟故障传播、诊断和推理过程中的不足，提出模糊故障Petri网的概念及其建模方法，分一因一果、一因多果、多因一果和竞争模式4种情况定义变迁发生的规则和后果，以此模拟系统的动态运行过程，反映故障传播的固有特性。将模糊故障Petri网的建模方法应用于故障推理与诊断，提出将正向推理和反向推理相结合，并给出相应的推理算法，用泵站机组压力不足的实例加以验证。研究结果表明：该方法既能模拟故障传播过程，又能进行模糊推理，实用性强。

关键词：模糊故障Petri网；正向推理；反向推理

中图分类号：TP391             文献标志码：A         文章编号：1672-7207(2013)01-0208-08

Modeling method of fuzzy fault Petri nets and its application

HUANG Min, LIN Xiao, HOU Zhiwen

(College of Computer and Communication Engineering, Changsha University of Science and Technology, Changsha 410014, China)

Abstract: In order to overcome the shortcomings of simulating fault spreading, diagnosis and reasoning in fuzzy Petri nets and fault Petri nets, the concept and modeling method of fuzzy fault Petri nets ware put forward. The transition rules and consequences were defined from four types, i.e, one cause and one effect, one cause and several effects, several causes and one effect, competition pattern, to simulate the dynamic running process and reflect the inherent characteristics of the fault spreading. By applying the modeling method of fuzzy fault Petri nets in fault reasoning and diagnosis, the thought of combining the forward reasoning and backward reasoning was proposed, and corresponding algorithm was given. This method was verified by the example of insufficient pressure of hydraulic system. The results show that the forward reasoning can simulate the process of fault spreading, and backward reasoning can carry out fuzzy reasoning perfectly, and so the method is practical.

Key words: fuzzy fault Petri nets; forward reasoning; backward reasoning

在进行故障诊断与推理过程中，往往存在很多不确定性。何新贵等^[1-7]提出模糊Petri网的建模方法，将Petri网与模糊技术相结合，提出许多不同形式的模糊Petri网；Loony等^[5]将1个模糊标识连接到1个place，对其中具有不确定性的token数进行分析，由系统外赋予确定性。刘心等^[6]对基于模糊Petri网的时间推理模型进行了讨论，将1个模糊标识连接到每个标识的place，place的模糊集给出其特征。韩光臣等^[7]运用模糊产生式规则进行推理，并提出了“与模式”、“或模式”的推理方法，反映了一定的客观性。这些方法虽然都统称为模糊Petri网，但目前还没有统一的定义，且内涵不相同，故障传播的固有特性得不到体现，如A故障导致B故障，在没有得到修复之前A故障并不会消失；而在模糊Petri网的运行规则中，A到B间的变迁发生后，A中的托肯会传到B中，给人造成A的故障传给B后就消失的错觉。李厦等^[8-9]提出故障Petri网的建模方法，通过增加变迁时间标签集合来记录故障传播路径，较好地体现了故障传播的固有特性，但很难根据已经发生的目标故障进行反向推理以寻找故障源。为此，本文作者综合故障Petri网和模糊Petri网的优点，提出模糊故障Petri网(Fuzzy Fault Petri Net，简称FFPN)的概念，并对其建模方法和应用进行研究。

1  模糊故障Petri网的概念

定义1 模糊故障Petri网定义为1个7元组(P,T,F; w,d,T_s,m₀)。其中：

(1) P={p₁，p₂，…，p_n}表示有限库所集合，且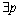∈P:^·p=0∧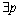∈P:p^·=0。^·p=0表示系统的初始条件，是系统运行前通过观察、测量或试验得到的，即原发性异常征兆，也就是潜在故障源；p^·=0表示系统产生的最终结果，即表现的目标故障。

(2) T={t₁，t₂，…，t_n}表示有限变迁集合，即部件的状态变化或行为动作，且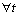∈T:|^·t|≥1∧|t^·|≥1。

(3) F 为流关系集合，dom(F)∪cod(F)= P∪T。其中：dom(F)={x|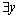：(x,y)∈F}，cod(F)={x|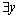：(y,x)∈F}分别为F的定义域和值域。

(4) w: F∈(0,1]，当p∈^·t时，w(p,t)表示库所p对变迁t成立的支持度，即变迁的输入权值，简写为w_I；当t∈p^·时，w(t,p)表示变迁t对库所p成立的支持度，即变迁的输出权值，简写为w_O；m(p)则表示库所p成立的可信度；w_I×m(p)表示库所p对变迁t的实际可信度。

(5) d: T∈(0,1]，表示变迁t对各个前提条件的实际支持度的最低要求,也就是变迁t的发生必须满足条件：

w_I×m(p)≥d(t)              (1)

(6) T_s(Translated Set)为已经发生过的变迁集合，初始时该集合为空，t_j发生后，

T_s= T_s +{t_j}                (2)

该集合标识故障的传播路径，同时可以防止变迁的反复发生，即同一故障发生后，在没有修复之前不会反复发生。因为变迁t发生后，只在后集库所中增加托肯，前集中的托肯不会消失，按照传统Petri网理论，该变迁t将会反复发生，这不符合实际情况。增加T_s 后，变迁t能否发生必须满足条件：

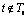                   (3)

(7) M₀={m₀(p₁),m₀(p₂),…,m₀(p_n)}∈(0,1]，称为初始可信度，一般通过历史数据、观察、测量、专家系统等途径获得。

2  模糊故障Petri网的建模方法

模糊故障Petri网的建模方法包括2个方面：一是根据系统的逻辑关系建立基本的Petri网模型，二是根据变迁发生规则来模拟系统的动态运行过程。基本的Petri网模型见文献[8]，本文对定义变迁发生规则进行重点研究。

模糊故障Petri网的变迁发生规则应该能够反映故障信息传播的固有特点，在故障传播过程中，有一因一果、多因一果、一因多果、竞争模式和多因多果共5种传播模式，涉及合成模糊产生式规则，即在模糊产生式规则中的前提或结论部分包含连接词“与”、“或”。本文采用MYCIN系统^[9]中基于可信度的方法，基本思想是合取式的真值取各子式真值的最小值，析取式的真值取各子式真值的最大值。此方法在专家系统中应用广泛^[10-16]。

在5种故障传播模式中，多因多果模式没有确定的结论产生，不能进行演绎推理，在知识库中不允许出现，因此，本文不给出定义。以下分4种模式来定义变迁发生的条件和后果。

2.1  一因一果模式

这种模式的产生式规则是：IF p₁(m₁,w₁) THEN(d) p₂(w₂, m₂)，如图1所示。

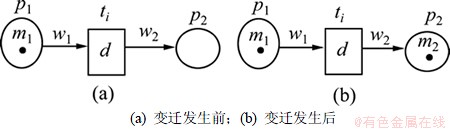
图1  一因一果模式的模糊故障Petri网表示

Fig.1  FFPN show of one cause and one effect pattern

定义2 变迁发生条件。在当前标识M下，变迁t_i有发生权，必须同时满足式(1)和(3)。

定义3 变迁发生后果。在此，先定义函数：

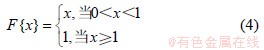
在当前标识M下，变迁t_i发生后，执行式(2)，且

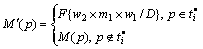       (5)

2.2  多因一果模式

产生式规则是：IF p₁(m₁,w₁) AND p₂(m₂, w₂) AND…AND p_i(m_i,w_i)THEN(d) p_k(w_k, m_k)，即^·t={p₁, p₂, …, p_i}，t^·={p_k}，如图2所示。

定义4 变迁发生条件。在当前标识M下，变迁t_i有发生权，须满足式(3)外，还要满足：

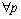∈^·t_i，min(m₁×w₁, m₂×w₂，…，m_i×w_i)≥d     (6)

定义5 变迁发生后果。变迁t_i发生后，执行式(2)。

    (7)

F{x}的取值与式(4)的相同。

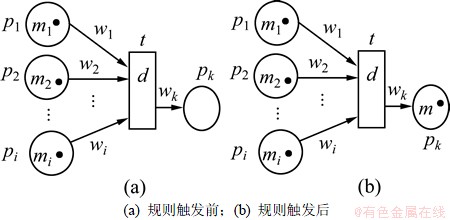
图2  多因一果模式的模糊故障Petri网表示

Fig.2  FFPN show of several causes and one effect pattern

2.3  一因多果模式

产生式规则是：IF p_j(m_j,w_j) THEN(d) p₁(m₁,w₁) AND p₂(m₂,w₂) AND …AND p_i(m_i,w_i)，即^·t={p_j}, t^·={p₁，p₂，…，p_i}，如图3所示。

这种模式的变迁发生条件与一因一果模式的变迁发生条件是相同的。

定义6 变迁发生后果。变迁t_i发生后，执行式(2)。

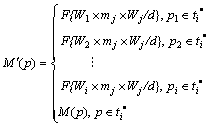      (8)

F{x}的取值与式(4)的相同。

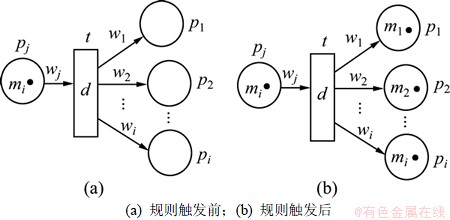
图3  一因多果模式的模糊故障Petri网表示

Fig.3  FFPN show of one cause and several effect patter

2.4  竞争模式模式

产生式规则是：IF p₁(m₁,w₁) OR p₂(m₂,w₂) OR …OR p_i(m_i,w_i) THEN(d₁,d₂,…,d_i) p_k(w_1k, w_2k,…,w_ik;m_k)，即t₁^·= t₂^·=…= t_i^·={p_k}，如图4所示。

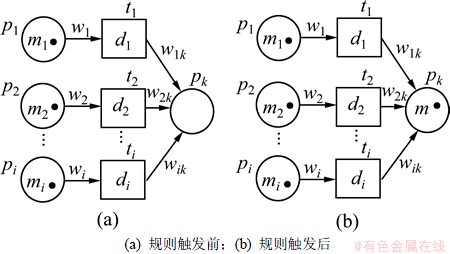
图4  竞争模式的模糊故障Petri网表示

Fig.4  FFPN show of competition pattern

这种模式的变迁发生条件与一因一果模式的变迁发生条件是相同的。

定义7 变迁发生后果。变迁T_i发生后，执行式(2)。

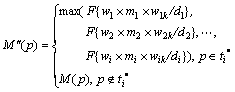      (9)

其中：F{x}的取值与式(4)的相同。

3  模糊故障Petri网的应用研究

模糊故障Petri网的实践意义在于故障推理与诊断。在故障诊断过程中，使用的推理方法一般有正向推理和反向推理。其中正向推理是根据已知条件推导可能产生的故障结果，用于监测信息比较完备的在线故障监测和诊断问题；反向推理是根据已经产生的故障结果来推导原因，以寻找故障源，需进行模糊推理，用于监测信息不太充分的离线故障诊断。使用模糊故障Petri网进行故障推理与诊断时，将正向推理和反向推理相结合，先用正向推理推导可能产生的故障，并对该环节采取措施加以防范，变“定期检修、被动维修”为“主动维护”；一旦出现故障，用反向模糊推理来寻找故障源，若正、反向推理的结论吻合，则说明诊断有效；若两者不吻合，则需要修改库所和变迁的可信度、阈值或权值，不断调整直到两者吻合为止，如图5所示。

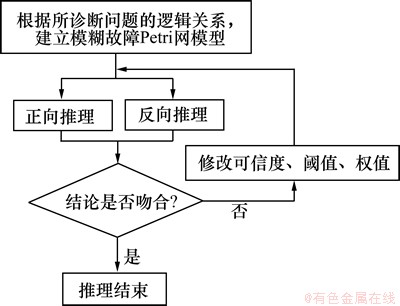
图5  模糊故障Petri网的诊断推理流程

Fig.5  Diagnosis reasoning process of FFPN

调整库所和变迁的可信度、阈值、权值的目的是为下一次诊断与推理作准备。因为这些值都是根据历史数据、观察等人为设定的，不一定符合每个阶段的实际情况，只有符合实际，推理才是有意义的。

3.1  正向推理算法

Step 1：根据所要诊断问题的逻辑关系，建立模糊故障Petri网模型。一些复杂系统的网模型可能比较庞大，可利用面向对象或高级Petri网技术进行化简。

Step 2：写出对应故障征兆和目标故障的初始库所和目标库所。

Step 3：确定模糊故障Petri网的初始标识M₀，通过观察、历史数据等确定各库所和变迁的初始可信度、权值和阈值；令T_s=φ。

Step 4：在当前标识M下，按一因一果、一因多果、多因一果和竞争模式4种情况计算有发生权的变迁t_i的发生后果，并插入T_s集合，即T_s=T_s+{t_i}。

Step 5：重复Step 4，直到没有变迁发生，即到达目标状态，判断其可信度是否大于等于阈值：若是，则说明该故障会发生；否则，系统正常。

Step 6：检查T_s集合，若相邻变迁之间有连接关系，则说明故障是连续传播的；否则，故障有多条传播路径，有多个目标状态。推理结束。

3.2  反向推理算法

由于反向推理是根据已经产生的故障结果来推导故障源，所以，会涉及回溯等概念。

定义8 设t_a为一变迁，p_i,p_j和p_k为3个库所，若p_i∈^·t_a，p_j∈t_a^·，则p_i称为p_j的立即回溯关联库所；若p_i是p_j的立即回溯关联库所，且p_j是p_k的立即回溯关联库所，则称p_i是p_k的回溯关联库所；若p_i∈^·t_a且p_k∈^·t_a，则称p_i和p_k为变迁t_a的邻近库所。包含p_i的立即回溯关联库所的集合称为p_i的立即回溯关联库所集合，表示为IHS(p_i)，包含p_i的回溯关联库所的集合称为p_i的回溯关联库所集合，表示为HS(p_i)。

反向推理算法步骤如下。

Step 1：初始目标库所(p_j, IHS(p_j), m(p_j))是1个终止节点。其中: p_j是目标库所，^· p_j=t_j，IHS(p_j)是目标库所p_j的立即回溯关联库所集合。设m(p_j)=1，表示故障已发生。

Step 2：按照变迁发生概率从大到小选择非终止节点(p_i, IHS(p_i),—)，“—”表示可信度未知。若IHS(p_i)=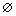，则标注此节点为终止节点。对每个终止节点，根据计算所得的可信度来判断是否与实际情况相符，若相符，则推理合法，终止节点变为(p_s,Ф,y_s)，推理结束；若不相符，则调整各变迁的权值和阈值以及库所的可信度，并按以下4种模式中的一种继续反向推理：

(1) 一因一果模式。如图6(a)所示，IHS(p_b)=p_a，节点(p_b, IHS(p_b), m(p_b))成为(p_a, IHS(p_a),m(p_a))，其中m(p_a)=F{[m(p_b)×d]/(w_pt×w_tp)}。初始时，m(p_b)=1, w_pt∈ (0,1], d∈(0,1], w_tp∈(0,1]，F{x}的计算与式(4)的相同。

(2) 多因一果模式。如图6(b)所示，IHS(p_z)= {p₁,p₂,…,p_n}，节点(p_z, IHS(p_z), m(p_z))成为(p₁, IHS(p₁), m(p₁)),(p₂, IHS(p₂),m(p₂)),…,(p_n,IHS(p_n),m(p_n))。其中：m(p₁)=F{[m(p_z)×d]/(w_p1t×w_tp)},m(p₂)=F{[m(p_z)×d]/ (w_p2t×w_tp)},…, m(p_n)=F{[m(p_z)×d]/(w_pn×w_tp)}。初始时，

m(p_z)=1, F{x}的计算与式(4)的相同。

(3) 一因多果模式。如图6(c)所示，节点(p₁, IHS(p₁),m(p₁)),(p₂, IHS(p₂),m(p₂)),…,(p_n, IHS(p_n),m(p_n))成为(p_a, IHS(p_a),m(p_a))。其中：m(p_a)= min(F{[m(p₁)×d]/ (w_pat×w_tp1)}，F{[m(p₂)×d]/(w_{pa t}×w_tp2)},…, F{[m(p_n)×d]/ (w_pat×w_tpn)})。初始时，m(p₁)= m(p₂)=…= m(p_n)=1。

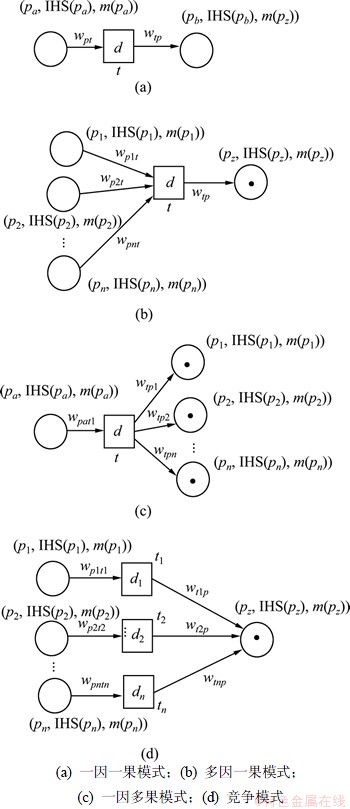
图6  反向推理的4种模式

Fig.6  Four kinds of pattern of backward reasonings

(4) 竞争模式。如图6(d)所示，则IHS(p_z)= {p₁,p₂,…,p_n}，节点(p_z, IHS(p_z), m(p_z))成为(p₁, IHS(p₁), m(p₁)), (p₂, IHS(p₂), m(p₂)), …, (p_n, IHS(p_n), m(p_n))。其中：m(p₁)=F{[m(p_z)×d]/(w_p1t1×w_t1p)}, m(p₂)=F{[m(p_z)×d]/ (w_p2t2×w_t2p)},…, m(p_n)= F{[m(p_z)×d]/(w_pntn×w_tnp)}。初始时，m(p_z) =1。F{x}的计算与式(4)的相同。继续往前推理时，应优先取m最大的分支。

在推理过程中，若要调整库所和变迁的可信度、权值、阈值，则需要判断当前值与目标值，当库所可信度的当前值大于目标值时，需根据实际情况增大变迁的输入、输出权值或缩小变迁的阈值。

4  应用实例及分析

液压系统在各种机械设备中得到广泛使用，会经常出现一些故障，如启动故障、启动时不能充满水、压力和流量不足、动力机超载、轴承发热、不正常响声、振动和噪声、填料密封过热和泄漏等^[8]。引起这些故障的原因很多, 这些原因和故障之间又相互影响，有时甚至互相循环，使得故障诊断十分复杂；另一方面，不同的工作状态也会影响液压系统的故障状态。在调试安装阶段，安装位置、相互配合之间的故障占主要部分；进入正常工作状态后，其他故障成为主要原因。根据该设备工作的逻辑关系和历史数据，得到如图7所示的某液压系统的模糊故障Petri网模型，其中库所的含义、初始可信度以及变迁的含义、初始权值和阈值见表1。

现假设该设备运转良好，没有发生故障，根据表1中的历史数据进行正向推理，即图7所示模型从左往右推。过程如下。

Step 1：t₁₁与t₁₂是竞争关系，由定义2，t₁₁有发生权，t₁₂没有发生权，p₆的可信度来自于t₁₁；由定义3，m(p₆)=0.63。T_s={t₁₁}。

Step 2：t₆，t₇，t₈和t₉这4个存在竞争关系，由定义2可知t₆和t₉没有发生权，t₇和t₈有发生权；由定义7可知：m(p₁)=max(m(p₇)×w_p7t7×w_t7p1/d₇, m(p₈)× w_p8t8×w_t8p1/d₈)=max(0.77,0.80)=0.80, T_s={t₁₁,t₈}。

Step 3：t₁₀是一因一果关系，由定义2可知t₁₀没有发生权，p₅的可信度为0，后继的t₅没有发生权。

Step 4：t₁，t₂，t₃和t₄是竞争关系，由定义2可知，t₄没有发生权，m(p₀)=max(m(p₁)×w_p1t1×w_t1p0/d₁, m(p₂)× w_p2t2×w_t2p0/d₂, (p₃)×w_p3t3×w_t3p0/d₃)=max(0.96, 0.89, 0.70)= 0.96；T_s={t₁₁,t₈,t₁}。

Step 5：p₀已是终止节点，推理结束。

正向推理的结论是：p₀中的故障是由p₈→ t₈→p₁→t₁产生的，并且要防范t₁₁。

推理过程如图8所示，图中有箭头穿进库所的，代表该库所中的值来自于箭头对应的变迁，即一组竞争变迁中箭头对应的变迁最有可能发生。

现假设p₀产生故障，采用反向推理来寻找故障源，推理过程如下。

Step 1：p₀已经产生故障，即m(p₀)=1。

Step 2：t₁，t₂，t₃，t₄和t₅是竞争关系，由3.2节中Step 2的竞争模式计算p₁，p₂，p₃，p₄和p₅的可信度：m(p₁)=0.84，m(p₂)=0.81，m(p₃)=0.99，m(p₄)=0.78，m(p₅)=0.82。

表1  图7中库所和变迁的含义及其初始可信度和权值

Table 1  Concept of place and transition, their initial credibility and weights in Fig.7

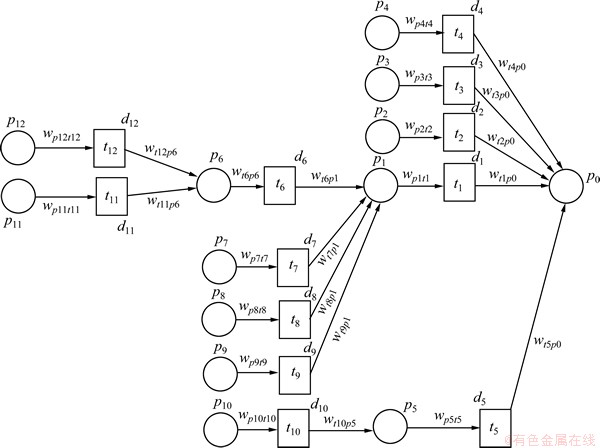
图7  某液压泵站机组的模糊故障Petri网模型

Fig.7  FFPN model of a hydraulic pump station

Step 3：可信度最大的p₃可能是故障源，通过检查，故障源不在这里，且与正向推理的结论不相符，需调整表1中的初始可信度、阈值或权值。

Step 4：由于p₃的可信度比实际的大，需增大t₃的输入和输出权值，现分别调整为0.85和0.88，此时，m(p₃)= 0.76，取p₁，p₂，p₃和p₄中可信度最大的p₁分支继续往回推。

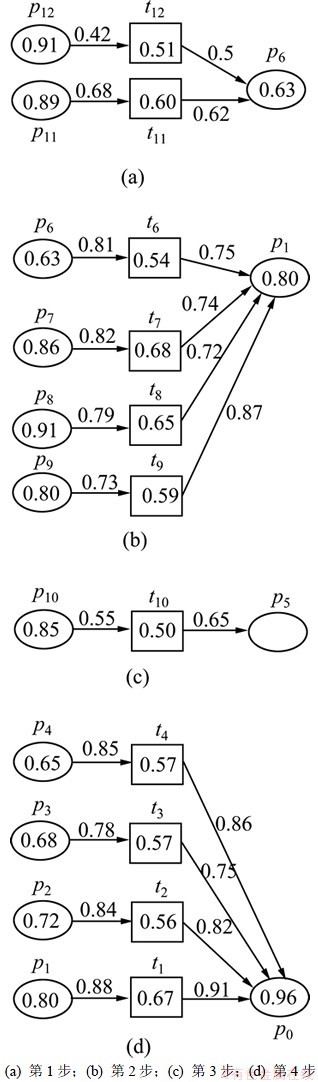
图8  实例的正向推理过程

Fig.8  Forward reasoning processes of an example

Step 5：p₁由t₆，t₇，t₈和t₉变迁的竞争而获得，计算得m(p₆)=0.75，m(p₇)=0.94，m(p₈)=0.96，m(p₉)= 0.78。可信度最大的是p₈，已是终止节点，通过实际检查，故障源就在这里，推理结束。

反向推理的结论是：p₀故障来自于p₈，与正向推理相符。

5  结论

(1) 为准确描述故障传播的固有特性，且便于根据故障信息定位故障源，提出模糊故障Petri网的概念是7元组(P,T,F; w,d, T_s,M₀)。

(2) 分一因一果、多因一果、一因多果和竞争模式4种情况分别定义变迁发生的条件和结果，其中基本条件是：W_I×m≥d,后果的共性是只改变后集库所的可信度，其他库所保持不变。

(3) 将模糊故障Petri网的理论应用于故障诊断，正向推理和反向推理相结合，正向推理用于记录故障的传播过程，反向推理用于根据已经发生的故障定位故障源。并提出算法步骤，调整库所和变迁的可信度、阈值、权值的方法，应用于液压泵站机组轴向柱塞泵压力不足的实例中，证明了这种故障诊断方法的正确性和可靠性。

(4) 下一步的研究工作是将模糊故障Petri网的建模方法和推理方法开发成软件工具，使其应用更加方便、快捷。

参考文献：

[1] 何新贵. 模糊Petri网[J]. 计算机学报, 1994, 17(12): 946-950.

HE Xingui. Fuzzy Petri nets[J]. Chinese Journal of Computes, 1994, 17(12): 946-950.

[2] 董玉梅, 张立臣. 模糊时间Petri网及扩展的模糊时间Petri网[J]. 计算机科学, 2005, 32(11): 241-246.

DONG Yumei, ZHANG Lichen. Fuzzy-timing Petri nets and extended fuzzy-timing Petri nets[J]. Scientific Journal of Computer Science, 2005, 32(11): 241-246.

[3] 韩光臣, 孙树栋, 司书宾, 等. 基于模糊概率Petri网系统的故障诊断仿真研究[J]. 计算机集成制造系, 2006, 12(4): 520-525.

HAN Guangchen, SUN Shudong, SI Shubin, et al. Research on fault diagnosis simulation based on Petri nets system[J]. Computer Integrated Manufacturing Systems, 2006, 12(4): 520-525.

[4] GAO Mei-mei, ZHOU Meng-chu, HUANG Xiao-guang, et al. Fuzzy reasoning Petri nets[J]. IEEE Transactions on Systems, 2003, 33(3): 341-323.

[5] Loony C G. Fuzzy Petri net for rule-based decision making[J]. IEEE Transactions on System Man, Cybren, System, Man and Cybernetics, 1988, 18(1): 178-183.

[6] 刘心, 印桂生, 张磊. 一种面向对象模糊Petri网建模方法的研究[J]. 计算机应用研究, 2009, 26(11): 4060-4062.

LIU Xin, YIN Guisheng, ZHANG Lei. Research on modeling method of object-oriented fuzzy Petri nets[J]. Application Research of Computers, 2009, 26(11): 4060-4062.

[7] 韩光臣, 孙树栋, 司书宾, 等. 复杂系统故障传播与故障分析模型研究[J]. 计算机集成制造系统, 2005, 11(6): 794-798.

HAN Guangchen, SUN Shudong, SI Shubin, et al. Research on model of fault diagnosis and propagation in complex system[J]. Computer Integrated Manufacturing Systems, 2005, 11(6): 794-798.

[8] 李厦. 基于Petri网的故障诊断技术研究及其在液压系统中的应用[D]. 上海: 同济大学机械工程学院, 2006: 64-67.

LI Sha. Petri nets-based fault diagnosis techniques with applications to hydraulic system[D]. Shanghai: Tongji University. College of Mechanical Engineering, 2006: 64-67.

[9] 叶俊. 基于Petri Net的故障诊断理论研究及其在磁浮列车上的应用[D]. 长沙: 国防科技大学机电工程与自动化学院, 2005: 9-13.

YE Jun. Fault diagnosis theory research based on petri nets and its applications to maglev train[D]. Changsha: National University of Defense Technology. College of Mechanical Engineering and Automation, 2005: 9-13.

[10] 袁崇义. Petri网原理与应用[M]. 北京: 电子工业出版社, 2005: 12-22.

YUAN Chongyi. Petri net principle and application[M]. Beijing: Press of Electronics Industry, 2005: 12-22.

[11] 刘海荣, 刘金琨. 基于MYCIN不精确推理的专家系统C++程序设计[J]. 计算机工程与设计, 2001, 22(2): 47-51.

LIU Hairong, LIU Jinkun. Expert system C++ program design based on MYCIN inexact inference[J]. Computer Engineering and Design, 2001, 22(2): 47-51.

[12] 范贵生, 虞慧群, 陈丽琼, 等. 基于Petri网的服务组合故障诊断与处理[J]. 软件学报, 2010, 21(2): 231-247.

FAN Guisheng, YU Huiqun, CHEN Liqiong, et al. Fault diagnosis and handling for service composition based on petri nets[J]. Journal of Software, 2010, 21(2): 231-247.

[13] 苏春, 沈戈, 许映秋. 基于随机故障Petri网的液压系统可靠性建模与分析[J]. 液压与气动, 2006, 29(6): 29-31.

SU Chun, SHEN Ge, XU Yingqiu. Hydraulic system reliability modeling and analysis based on stochastic failure Petri net[J]. Hydraulic and Pneumatic, 2006, 29(6): 29-31.

[14] 化建宁. 故障Petri网及其在机械设备剩余寿命预测中的应用[D]. 保定: 河北农业大学机电工程学院, 2001: 35-45.

HUA Jianning. Fault Petri net and its application in the remained life prediction of machinery[D]. Baoding: Agricultural University of Hebei. College of Mechanical and Electrical Engineering, 2001: 35-45.

[15] 包玉剑. 基于加权模糊Petri网的输电网故障诊断方法研究[D]. 成都: 西南交通大学电气工程学院, 2009: 35-39.

BAO Yujian. The fault diagnosis method of power transmission system using weight fuzzy Petri net[D]. Chengdu: Southwest Jiaotong University. College of Electrical Engineering, 2009: 35-39.

[16] 黄敏, 魏伟. 一种有时间约束的复杂Petri网建模方法研究[J]. 中南大学学报: 自然科学版, 2012, 43(3): 1027-1032.

HUANG Min, WEI Wei. One modeling method research of complex Petri nets with timing constraint[J]. Journal of Central South University: Science and Technology, 2012, 43(3): 1027-1032.

(编辑  陈灿华)

收稿日期：2012-02-08；修回日期：2012-04-22

基金项目：湖南省科技计划项目(2011GK3113)

通信作者：黄敏(1968-)，女，重庆人，副教授，硕士研究生导师，从事Petri网理论及其应用研究；电话：13548718081；E-mail:huangmin_09@yahoo.com.cn