
J. Cent. South Univ. (2018) 25: 1958-1965
DOI: https://doi.org/10.1007/s11771-018-3886-5
Fatigue life evaluation on key components of high-speed railway catenary system
QI Guang-feng(戚广枫), XIAO Xiao-hui(肖晓晖), ZHAO Hui(赵慧), CHEN Jian-fang(陈建芳)
School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract: The fatigue load spectrum and operation life evaluation of key components in the catenary system under the high speed train running condition were investigated. Firstly, based on the catenary model and pantograph model, the couple dynamic equations of pantograph–catenary were built with the Lagrange’s method; then the dynamic contact force was obtained by the Newmark method at the train speeds of 250, 280 and 300 km/h, respectively. Secondly, the finite element model (FEM) of one anchor section’s catenary was built to analyze its transient response under the contact force as train running; then the loading time history of messenger wire base, steady arm, registration tube, oblique cantilever, and straight cantilever were extracted. Finally, the key components’ fatigue spectrum was carried out by the rain-flow counting method, and operation life was estimated in consideration of such coefficients, such as stress concentration, shape and dimension, surface treatment. The results show that the fatigue life of the catenary system reduces with the increasing of train speed; specifically, the evaluated fatigue life of the steady arm is shorter than other components.
Key words: fatigue spectrum; fatigue life evaluation; pantograph–catenary’s contact force; high-speed railway
Cite this article as: QI Guang-feng, XIAO Xiao-hui, ZHAO Hui, CHEN Jian-fang. Fatigue life evaluation on key components of high-speed railway catenary system [J]. Journal of Central South University, 2018, 25(8): 1958–1965. DOI: https://doi.org/10.1007/s11771-018-3886-5.
1 Introduction
The catenary system, whose role is to supply power to electric high-speed locomotive, is erected along the railway on field and has no standby but bears long-term dynamic load such as natural wind and the pantograph–catenary contact force during the process of train running. So, fatigue is one of the main failure modes. Meanwhile, the failure statistical data of the railway traction power system show that the suspension system, steady arm, and supporting device are all liable to fatigue failure [1, 2]. However, recently the failure evaluation available on the catenary focuses on its suspension system [3–6] and little attention has been paid to the steady arm and supporting device.
The credibility of fatigue evaluation depends upon the fatigue model (object), fatigue evaluation method, and determination of dynamic load. Specific to the determination of fatigue model and dynamic load of the catenary system, VINAYAGALINGAM [7] and SEO et al [8] built the model of catenary with the Euler–Bernoulli beam elements; SONG et al [9, 10] established a catenary model using nonlinear cable and truss elements. MORRIS et al [11] used the pantograph as 2-DOF mass-spring-damp model and simplified the catenary as concentrated mass point; ZHANG et al [12] and MEI [13] built the FEM of catenary, calculated the contact force by simulating pantograph-catenary system, and obtained the dynamic response of contact wire unit by assuming the contact force as the external load of the catenary model; ARNOLD et al [14, 15] proposed a descriptor form that subsumed a certain class of mechanical systems with constraints under the term partial differential-algebraic equation (PDAE); JIMENEZ-OCTAVIO et al [16] adopted a moving mesh algorithm integrated into a general finite element method which demonstrated flexibility and advantages against traditional meshing techniques. CHENG [17] developed a model of the simple chain/simple catenary with the Lagrange’s equation; and then calculated the contact force with the pantograph–catenary coupling model. QI et al [18] assumed the pantograph–catenary contact force equivalent to a constant force by reference to analytical data of the pantograph–catenary experiment.
The researches mentioned above were limited on analyzing the pantograph–catenary coupling contact force, or using the contact force as the external load for dynamic response analysis of catenary system. But little research has been done with respect to the fatigue of catenary system based on the dynamic performance of pantograph– catenary system, especially for the high-speed railway catenary.
Specific to the fatigue and residual life evaluation, MAI et al [3] took the extended finite element method to study the fatigue crack growth of contact wire; BI et al [19] analyzed the fatigue life of contact wire based on the rain-flow counting method; PENG [20] adopted the simplified load spectrum method to estimate the fatigue life of contact wire only taking the maximum and minimum values of stress spectrum. To sum up, the researches mainly focus on the fatigue life analysis of contact wire, rather than that of steady arm or supporting device.
Above all, the mathematical models of catenary have been built and only used to analyze the coupled current-receiving quality or system dynamic response; while researches on fatigue mainly focused on the fatigue of contact wire.
Therefore, this paper deduced the dynamic equation of pantograph–catenary coupled system with Lagrange’s equation to obtain the contact force time history, which was then loaded to the finite element model of catenary. Then the fatigue load spectra of those key components of the catenary system under train running conditions were carried out using rain-flow counting method. At the speeds of 250, 280 and 300 km/h, the fatigue life of high-speed railway catenary system was evaluated considering pantograph–catenary coupled dynamic effect.
2 Contact force calculation based on pantograph–catenary coupled model
2.1 Model of catenary system
The catenary system is composed of contact wire, support wire, dropper, supporter, and steady arm. The simple catenary model of 3 spans in one section is shown in Figure 1, where SA and SB are the tensions of contact wire and support wire, respectively; ρA and ρB are the linear densities of contact wire and support wire, respectively; kTi is the equivalent stiffness of the ith supporter; mATi and mBTiare the equivalent masses of the ith supporter and steady arm, respectively; kDiand mDiare the ith equivalent stiffness and half equivalent mass of the dropper; p and w are the numbers of droppers and supports, respectively; L is the length of one section.
As the support wire and contact wire are connected with the fixed ball joint at each terminal of one section, both their displacements and bending moments are zero and the displacement of support wire [21] and contact wire are expressed as:
 (1)
(1)
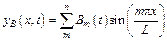 (2)
(2)
where Am and Bm are the mth amplitudes of contact wire and support wire.

Figure 1 Model of a 3-span simple catenary system
2.2 Model of pantograph
The pantograph is simplified to a 2-DOF spring-mass model as shown in Figure 2.
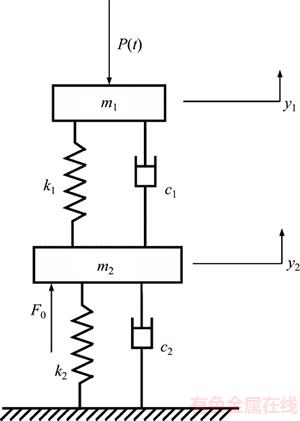
Figure 2 Model of pantograph
The dynamic equations of pantograph are:
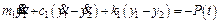 (3)
(3)
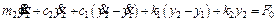 (4)
(4)
where m1, c1 and k1 are the equivalent mass, damping, and stiffness of pantograph panhead, respectively; m2, c2 and k2 are the equivalent mass, damping, and stiffness of pantograph frame, respectively; y1, 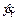 and
and 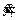 are the displacement, velocity, and acceleration of pantograph panhead, respectively; y2,
are the displacement, velocity, and acceleration of pantograph panhead, respectively; y2, 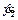 and
and 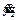 are the displacement, velocity, and acceleration of pantograph frame, respectively; P(t) is the dynamic contact force between catenary and pantograph; F0 is the static uplift force of the pantograph.
are the displacement, velocity, and acceleration of pantograph frame, respectively; P(t) is the dynamic contact force between catenary and pantograph; F0 is the static uplift force of the pantograph.
2.3 Coupled dynamic model of pantograph– catenary system
The dynamic equations of the pantograph- catenary system are deduced based on Lagrange method. The generalized coordinates of the pantograph–catenary system include Am, Bm, y1 and y2, regardless of the damping of catenary. So, the external forces of entire pantograph–catenary system only include the damping force of pantograph and the uplift force of pantograph frame.
For catenary, if the order of modal reduction is N, the generalized DOFs of catenary will be 2N. With the additional 2-DOF on pantograph panhead and frame, the generalized DOFs of entire pantograph–catenary system are 2N+2. The dynamic equilibrium equation of pantograph– catenary system in matrix form is expressed:
 (5)
(5)
where Y, 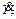
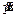 are generalized displacement matrix, velocity matrix, acceleration matrix; F is the force matrix; M, C and K are the mass matrix, damping matrix and stiffness matrix, respectively.
are generalized displacement matrix, velocity matrix, acceleration matrix; F is the force matrix; M, C and K are the mass matrix, damping matrix and stiffness matrix, respectively.
The dynamic contact force between catenary and pantograph P(t) is calculated by the displacements of pantograph panhead and catenary [22]:
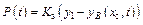 (6)
(6)
where Ks is the contact stiffness; yB(xc, t) is the displacement of catenary on contact point when pantograph moves to xc.
When the pantograph moves along the contact wire, the stiffness matrix of pantograph–catenary system changes constantly. So, the differential equation of pantograph–catenary system belongs to second-order change coefficient differential equation. And the equation can be solved by Newmark method, then the contact force can be calculated in each sampling time using Eq. (6).
3 Load spectrum and fatigue life evaluation
3.1 Load spectrum
The load spectra of components are obtained by taking following steps of transient response analysis of catenary’s model, extraction of load-time history and rain-flow counting.
Firstly, the finite element method is used to perform the transient response of the catenary system. The cantilever structure is simplified as a model constituted by beam element, pipe element and link element [20]. The cantilever pedestal is coupled with the brace and modeled as beam element, such components as the insulator chains; cantilever and registration tube are modeled as pipe element considering their structural stressing characteristic; the registration support is modeled as the bar element due to both ends’ hinging and only bear axial tensile stress; the support wire, contact wire and dropper are simulated with the bar element. Take the contact force obtained through solving the coupling equation of pantograph–catenary onto such model as the external load and perform transient response analysis on the catenary system by taking the Full method.
Then, the stress–time history corresponding to those key components as steady arm/registration tube, cantilever, etc. can be extracted as the corresponding loading history and then be counted using the rain-flow counting method to obtain the stress amplitude, stress mean value and their corresponding stress cycle number. To form the standard load spectrum, the stress cycle is converted through the Goodman line [23] to obtain zero mean equivalent stress value:
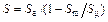 (7)
(7)
where S is the zero mean stress amplitude; Sa is the stress amplitude; Sm is the stress average; and Sμ is the material ultimate strength.
3.2 Fatigue life evaluation
On the basis of the above load spectrum, the fatigue life of the key components can be evaluated via the finite life design method. First, the stress and strain of dangerous zone under pantograph– catenary coupled load is calculated by using Pro/E and ANSYS. Then the fatigue loads are amended considering comprehensive factors such as stress concentration coefficient kt, shape and dimension coefficient ε, and surface treatment coefficient βs1.
According to the reliability evaluation of the catenary system [1], the reliabilities of the catenary supporting and positioning devices are 0.98 and 0.95, respectively. With reference to the P-S-N curve of their corresponding materials, the damages to components caused by the stress cycle are accumulated based on Miner linear fatigue cumulative damage rule [23]:
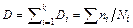 (8)
(8)
Comparing to the standard load spectrum under typical train operation condition, the fatigue life can be expressed with the times of train travelling.
4 Results analysis
Take one anchor section of catenary system of the high-speed railway from Wuhan to Guangzhou in China to perform evaluation, of which the specific parameters are listed in Table 1. The contact force versus pantograph position was obtained by solving catenary–pantograph coupled dynamic equations using Newmark method under the train speed of 250, 280 and 300 km/h. Figure 3 shows the contact force curve versus pantograph position.
Table 1 Specific parameters of catenary and pantograph
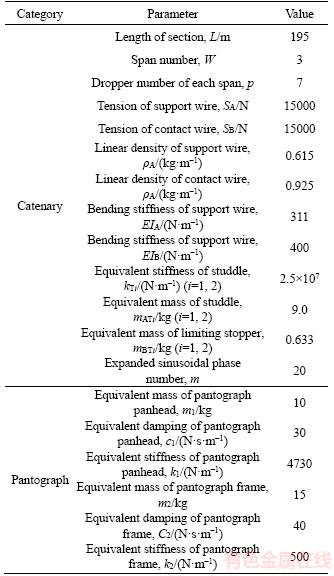
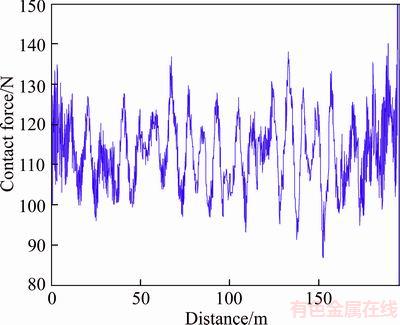
Figure 3 Contact force versus pantograph position at train speed of 250 km/h
According to the field running failure report and stress statistics of dynamic response simulation, we choose five key components of the catenary, i.e., messenger wire base, steady arm, registration tube, oblique cantilever and straight cantilever, which all follow the railway industry standards [24]. The loading–time history of steady arm and registration tube under three sets of train speed conditions is shown in Figure 4.
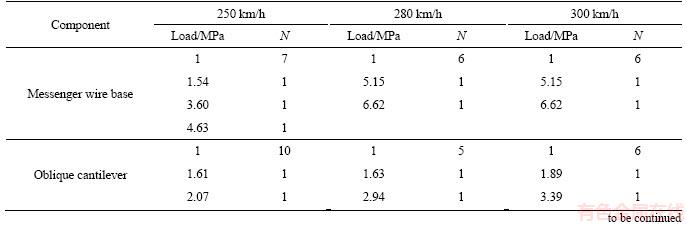
Parts of the load statistical histograms are shown in Figure 5. According to Goodman linear model, the zero mean loads were obtained. Removing those zero frequency combinations after counting statistics, the fatigue load statistics data are listed in Table 2.
The fatigue life was calculated after static stress analysis of steady arm or registration tube. Results of the allowed running times for each components of the registration device are shown in Table 3.
The rules of those key parts fatigue life are analyzed as follows:
1) The fatigue life of the key part of catenary dramatically declines with the increase of train running speed.
2) The rank of fatigue life of key parts from long to short is: messenger wire base, straight cantilever, oblique cantilever, and registration tube and steady arm.
3) When the train speed reaches 300 km/h, the fatigue life of steady arm reduces to 7.23×105 times,which is about half that of registration tube, and about one third of the cantilevers.
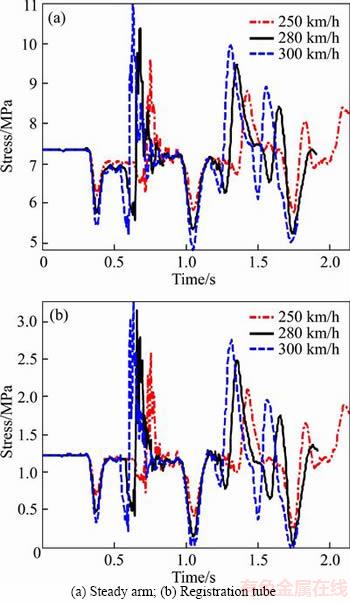
Figure 4 Loading–time history under three sets of train speed conditions:
5 Conclusions
1) The coupled model of catenary–pantograph has been built to acquire the contact force, which was loaded to perform the transient response analysis of catenary system; The dynamic time history of the key parts of the catenary system was extracted and then counted with rain-flow method and Goodman line to form their standard fatigue load spectrum.
2) According to the theory of structural fatigue damage, the fatigue life of those key parts has been evaluated considering the materials P-S-N curves and comprehensive coefficients such as stress concentration coefficient, shape and dimension coefficient, and surface treatment coefficient.
3) The evaluation results show that the fatigue life of the key part of catenary dramatically declines with the increase of train running speed. It is recommended that the design of support cantilever and steady arm should be revised.
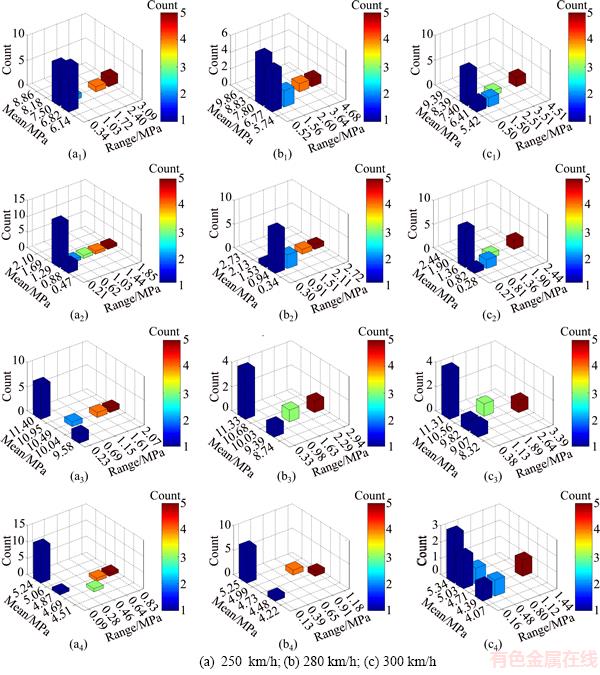
Figure 5 Histogram using rain-flow counting method for registration tube (a1, b1, c1), steady arm (a2, b2, c2), oblique cantilever (a3, b3, c3) and straight cantilever (a4, b4, c4) under three sets of train speed conditions:
Table 2 Load spectrum of key components
Continued
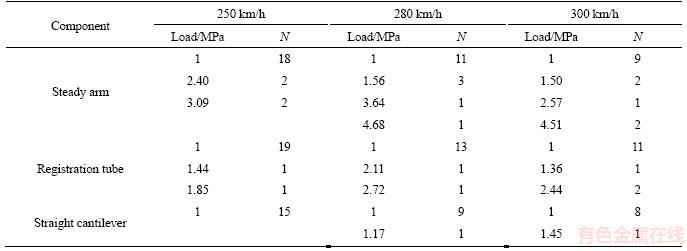
Table 3 Fatigue life of key parts

References
[1] QI Guang-feng. RAMS of high speed railway catenary system [M]. Beijing: Southwest Jiaotong University Press, 2012: 111–118. (in Chinese)
[2] SONG Xiao-dong, FU Yan-bing, CHEN Zhi-ya, LIU Heng-bin. Environmental impact evaluation for high-speed railway [J]. Journal of Central South University, 2014, 21(6): 2366–2371.
[3] MAI S H, NGUYEN-TAJAN M L, VERRIER A, ETIENNE B. Fatigue crack growth in the contact wire of railway catenary [C]// 13th International Conference on Fracture. Beijing, China: ICF, 2013: 16–21.
[4] JEAN P M, NGUYEN-TAJAN M L, HABIBOU M, SONG Dong-lin, ZHOU Ning. Fatigue analysis of catenary contact wire for high speed trains [C]// 9th World Congress on Railway Research. Lille, France, 2011: 1–11.
[5] WANG Xiao-yang, ZHANG Wei-hua, LI Rui-ping, SONG Dong-li, ZHOU Ning. Fatigue life prediction of elastic stitched catenary based on nominal method [J]. Computer Aided Engineering, 2014, 23(6): 8–11. (in Chinese)
[6] BI Ji-hong, REN Hong-peng. The fatigue analysis on the elastic chain flexible suspension catenary system based on rain-flow counting [J]. Journal of Railway Science and Engineering, 2012, 9(1): 61–67. (in Chinese)
[7] VINAYAGALINGAM T. Computer evaluation of controlled pantographs for current collection from simple catenary overhead equipment at high speed [J]. Journal of Dynamic Systems Measurement and Control, 1983, 105(4): 287–294.
[8] SEO J H, KIM S W, JUNG I H, PARH T W, MOK J Y, KIM Y G, GHAI J B. Dynamic analysis of a pantograph-catenary system using absolute nodal coordinates [J]. Vehicle System Dynamics, 2006, 44(8): 615–630.
[9] SONG Y, LIU Z, WANG H, LU X, ZHANG J. Nonlinear modelling of high-speed catenary based on analytical expressions of cable and truss elements [J]. Vehicle System Dynamics, 2015, 53(10): 1455–1479.
[10] SONG Y, LIU Z, WANG H, LU X, ZHANG J. Nonlinear analysis of wind-induced vibration of high-speed railway catenary and its influence on pantograph–catenary interaction [J]. Vehicle System Dynamics, 2016, 54(6): 723–747.
[11] MORRIS R B. The application of an analogue computer to a problem of pantograph and overhead line dynamics [J]. Proceedings of the Institution of Mechanical Engineers, 1964, 179(25): 782–808.
[12] ZHANG Wei-hua, LIU Yi, MEI Gui-ming. Evaluation of the coupled dynamical response of a pantograph-catenary system contact force and stress [J]. Vehicle System Dynamics, 2006, 44(8): 645–658.
[13] MEI Gui-ming. The dynamic study of pantograph/catenary system [D]. China: Southwest Jiaotong University, 2010. (in Chinese)
[14] ARNOLD M, SIMEON B. Coupling DAEs and PDEs for simulation the interaction of pantograph and catenary [J]. Mathematical and Computer Modelling of Dynamical Systems, 2000, 6(2): 129–144.
[15] ARNOLD M, SIMEON B. Pantograph and catenary dynamics: A benchmark problem and its numerical solution [J]. Applied Numerical Mathematics, 2000, 34: 345–362.
[16] JIMENEZ-OCTAVIO J R, CARNICERO A, SANCHEZ- REBOLLO C, SUCH M. A moving mesh method to deal with cable structures subjected to moving loads and its application to the catenary-pantograph dynamic interaction [J]. Journal of Sound and Vibration, 2015, 349: 216–229.
[17] CHENG Wei. Research on the current-collecting traits of electrified railway’s pathograph-catenary system [D]. China: Southwest Jiaotong University, 2007. (in Chinese)
[18] QI Guang-feng, CHEN Jian-fang, XIAO Xiao-hui, SONG Yun-chao. Fatigue load spectrum of key parts of high-speed railway catenary [J]. Journal of the China Railway Society, 2015, 37(10): 48–53. (in Chinese)
[19] BI Ji-hong, CHEN Hua-li, REN Hong-peng. Analysis on fatigue life of contact wire based on rain-flow counting method [J]. Journal of the China Railway Society, 2012, 34(6): 35–39. (in Chinese)
[20] PENG Zai-heng. Using TCL/TK designs the intefaces of pantograph-catenary coupling system and fatigue analysis [D]. China: Tianjin University, 2010. (in Chinese)
[21] ZHANG Wei-hua, SHENG Zhi-yun. The dynamic study of the catenary system [J]. Journal of the China Railway Society, 1992, 13(4): 26–33. (in Chinese)
[22] ZHOU Ning, ZHANG Wei-hua. Investigation on dynamic performance and parameter optimization design of pantograph and catenary system [J]. Finite Elements in Analysis and Design, 2011, 47: 288–295.
[23] CHEN Chuan-yao. Fatigue and fracture [M]. Whuhan: Huazhong University of Science and Technology Press, 2002: 3–33. (in Chinese)
[24] TB/T 2075.1–2075.23-2010. The railway industry standard of the People’s Republic of China [S]. (in Chinese)
(Edited by YANG Hua)
中文导读
高铁接触网关键零部件的疲劳寿命分析
摘要:本文研究了高速铁路接触网系统关键零部件在高速行车工况下的疲劳载荷谱和运行寿命。首先,基于受电弓模型与接触网模型,采用Lagrange法建立弓–网耦合动力学模型;采用Newmark法计算在250, 280 和300 km/h 3种行车速度下相应的动态接触力。其次,建立一个锚段内接触网的有限元模型,在行车工况的动态接触力作用下,计算接触网系统的瞬态响应;提取承力索、定位器、定位管、斜腕臂、直腕臂的载荷时间历程。最后,采用雨流计数法,统计得到关键零件的疲劳载荷谱,并考虑零件的应力集中系数、形状与尺寸系数、表面处理系数,进行寿命评估。结果表明:随着运行车速的提高,接触网的疲劳寿命会下降,其中定位器的疲劳寿命最短。
关键词:疲劳载荷谱;疲劳寿命评估;弓–网接触力;高速铁路
Foundation item: Project(51175383) supported by the National Natural Science Foundation of China (NSF)
Received date: 2016-03-30; Accepted date: 2016-06-06
Corresponding author: XIAO Xiao-hui, PhD, Professor; Tel: +86-27-68772247; E-mail: xhxiao@whu.edu.cn; ORCID: 0000-0002- 8212-2452