用于研究纤维尾砂胶结充填材料单轴压缩性能的新型人工智能模型
来源期刊:中国有色金属学报(英文版)2021年第4期
论文作者:喻智 史秀志 陈新 周健 齐冲冲 陈秋松 饶帝军
文章页码:1087 - 1102
关键词:纤维尾砂胶结充填材料;单轴抗压强度;预测;极限学习机;樽海鞘算法
Key words:fiber-reinforced cemented paste backfill; unconfined compressive strength; prediction; extreme learning machine; salp swarm algorithm
摘 要:为降低纤维尾砂胶结充填材料单轴压缩强度数据的获取难度,综合分析常规充填材料参数与纤维参数对其单轴压缩性能的影响,结合元启发式算法(樽海鞘算法, SSA)与极限学习机技术(ELM),提出一种新型人工智能模型(SSA-ELM)。为检验模型可靠性,开展720组不同灰砂质量比、固体质量浓度、纤维含量、纤维长度和养护时间的纤维尾砂胶结充填材料单轴抗压实验以建立充填材料强度性能数据库。研究结果表明,训练好的SSA-ELM模型能够准确地预测纤维尾砂胶结充填材料的单轴压缩强度,其性能优于ANN、SVR和ELM方法;纤维含量和纤维长度对纤维尾砂胶结充填材料单轴压缩性能具有重要影响。
Abstract: To reduce the difficulty of obtaining the unconfined compressive strength (UCS) value of fiber-reinforced cemented paste backfill (CPB) and analyze the comprehensive impact of conventional and fiber variables on the compressive property, a new artificial intelligence model was proposed by combining a newly invented meta-heuristics algorithm (salp swarm algorithm, SSA) and extreme learning machine (ELM) technology. Aiming to test the reliability of that model, 720 UCS tests with different cement-to-tailing mass ratio, solid mass concentration, fiber content, fiber length, and curing time were carried out, and a strength evaluation database was collected. The obtained results show that the optimized SSA-ELM model can accurately predict the uniaxial compressive strength of the fiber-reinforced CPB, and the model performance of SSA-ELM model is better than ANN, SVR and ELM models. Variable sensitivity analysis indicates that fiber content and fiber length have a significant effect on the UCS of fiber-reinforced CPB.
Trans. Nonferrous Met. Soc. China 31(2021) 1087-1102
Zhi YU, Xiu-zhi SHI, Xin CHEN, Jian ZHOU, Chong-chong QI, Qiu-song CHEN, Di-jun RAO
School of Resources and Safety Engineering, Central South University, Changsha 410083, China
Received 15 March 2020; accepted 28 January 2021
Abstract: To reduce the difficulty of obtaining the unconfined compressive strength (UCS) value of fiber-reinforced cemented paste backfill (CPB) and analyze the comprehensive impact of conventional and fiber variables on the compressive property, a new artificial intelligence model was proposed by combining a newly invented meta-heuristics algorithm (salp swarm algorithm, SSA) and extreme learning machine (ELM) technology. Aiming to test the reliability of that model, 720 UCS tests with different cement-to-tailing mass ratio, solid mass concentration, fiber content, fiber length, and curing time were carried out, and a strength evaluation database was collected. The obtained results show that the optimized SSA-ELM model can accurately predict the uniaxial compressive strength of the fiber-reinforced CPB, and the model performance of SSA-ELM model is better than ANN, SVR and ELM models. Variable sensitivity analysis indicates that fiber content and fiber length have a significant effect on the UCS of fiber-reinforced CPB.
Key words: fiber-reinforced cemented paste backfill; unconfined compressive strength; prediction; extreme learning machine; salp swarm algorithm
1 Introduction
Cemented paste backfill (CPB) is a composite material consisting of tailings, binder, water and possible additives [1]. It has been widely accepted by mining companies worldwide because of its potential safety and environmental and financial benefits [1-4]. These advantages of CPB are dependent on its bearing ability to maintain the stability of the underground structure of the mine, and this bearing ability is determined by the mechanical properties of the CPB. In previous studies [5-8], to further reinforce the mechanical properties of CPB, adding high-performance fiber materials as additives for CPB preparation was proposed and studied by a few experts, and it has been illustrated to be an effective method to improve the tensile and compressive strengths of CPB in some successful cases. This is because the fibers play the role of flexible connection in the CPB, which promotes the CPB to form a more compact structural performance. The disordered distribution of fibers in the CPB can provide resistance to compression failure, tensile failure and shear failure. The fiber-reinforced CPB shows excellent tenacity, and promotes the CPB to maintain good integrity after being damaged by external force. However, in the field of concrete, it is generally accepted that adding fiber can significantly improve the tensile capacity of concrete, but it is not helpful to improve the compressive capacity [9,10]. This may be related to the difference in raw material compositions between concrete and CPB. The main aggregate of CPB is tailings, which are fundamentally different from building materials in composition and grain size. The usage of cement in CPB is much less than that in concrete due to the low mechanical properties and material cost requirements. Thus, the influence of fiber on the properties of CPB is quite different from that of concrete.
Unconfined compressive strength (UCS) is usually used to evaluate the performance of composite and rock materials [5,11,12]. According to the study of ERCIKDI et al [13] and KOOHESTANI et al [14], the bearing ability of CPB is usually estimated by UCS, so only the compressive properties of the fiber-reinforced CPB were investigated in this study. Normally, the UCS value of the CPB can be determined by experimental tests, which are simple and economical test methods. However, much investment is still needed in experiments and tests to further explore the reinforcement mechanism of fibers and establish the relationship model between the UCS and fiber parameters. Before that, many experiments were carried out to study the impact of various parameters on the strength of CPB, such as cement content, concentration, and curing time in previous studies [15-17]. Therefore, it is valuable to drive the search for efficient, accurate and low-cost methods for the strength evaluation of fiber-reinforced CPB.
One method that is often used to predict the UCS of the CPB by researchers includes establishing an empirical formula for describing the relationship between the strength and influencing parameters of the CPB. For example, a single-factor or multifactor fitting relationship is established between the UCS and concentration, and the cement-to-tailing mass ratio [18,19]. CHEN et al [20] proposed a fitting estimation equation between the UCS and fiber parameter reinforcement index. These empirical formulas often have high prediction accuracy under specific experimental conditions, but they are difficult to generalize. In addition, the empirical formula is based on the experiment and UCS test, and it is difficult to avoid destruction of the CPB specimen and the consumption of materials and costs. To avoid UCS tests to determine the strength of CPB, experts have proposed the utilization of ultrasonic pulse velocity (UPV) nondestructive method [21-23]. The propagation velocity of the shear wave in the CPB can effectively reflect the compactness of the CPB. By establishing a relationship between the UCS and the shear wave velocity, the strength of the CPB can be predicted. Although it is a nondestructive and efficient laboratory test method, reliable testing equipment and general prediction equations related to the UCS and UPV still need further development.
In addition to the above methods, the performance of predicting the UCS of the CPB based on its influencing variables using intelligent models has been tested in some studies [24-29]. For example, OREJARENA and FALL [24] developed an artificial neural network (ANN) to analyze the mechanical properties of CPB under sulfate attack and simulate the effect of input variables on UCS. The obtained results show that the predictive UCS values agree well with the experimental values. QI et al [25] utilized the genetic algorithm (GA) to select the optimal hyperparameters of gradient boosting machine (GBM) technology and obtained high accuracy of predictive performance. Additionally, a software program, namely, intelligent mining for backfill, was developed for CPB design in this study. LU et al [26] combined the gradient boosting regression tree (GBRT) and the particle swarm algorithm (PSO) to predict the UCS value based on an enlarged database and achieved satisfactory results. QI et al [27] tested the predictive performance of a hybrid PSO-ANN model by using 396 CPB specimens and found that the optimal ANN model is a quite accurate tool to predict CPB strength. In addition, some studies applied the artificial intelligence (AI) technology to CPB properties, such as the initial settling rate [28] and pressure drop [29]. Although AI technology was applied in the mechanical property analysis of CPB, the extreme learning method (ELM) was not tested in previous studies. Additionally, the mechanical properties of fiber-reinforced CPB are quite different from those of normal CPB materials. In addition, a predictive model is not suitable for all problems and the solutions of all field sites according to the famous No Free Lunch theorem. Therefore, the study of new machine learning technology in analyzing the UCS of fiber-reinforced CPB is quite meaningful for the development of CPB.
As mentioned above, it is believed that there are few studies on the strength evaluation of fiber-reinforced CPB by intelligent models that can reduce the waste of materials and costs caused by experiments and tests. Therefore, a new and high-precision predictive model of the SSA-ELM (salp swarm algorithm and extreme learning machine) model was proposed and utilized to predict the UCS of fiber-reinforced CPB in the present work. Compared to previous studies, the comprehensive effect of the cement-to-tailing mass ratio (CR), solid mass concentration (SMC), fiber content (FC), fiber length (FL), and curing time (CT) on the UCS value of fiber-reinforced CPB was discussed sufficiently.
2 Experimental
2.1 Measurement of material properties
2.1.1 Tailings, binder and water
The tailings used to prepare the CPB were provided by a well-known lead and zinc production base, the Fankou Lead-Zinc Mine. More than 50000 t of fine-grained tailings are produced every year, and it is difficult to effectively use these tailings. The particle size distribution, chemical composition, and mineralogical compositions of the tailings were tested by LS particle size analysis, X-ray fluorescence spectrometry (XRF), and X-ray diffraction (XRD). Figure 1 indicates that the particle size of 47.15% particles in the tailings is smaller than 20 μm. Moreover, the XRD patterns and the physical and major chemical compositions of the tailings are shown in Fig. 2 and Table 1. After reviewing China’s Common Portland Cement Standard [30], Portland cement P.O 42.5R was selected as the binder in the fiber-reinforced CPB design. Its particle size distribution and basic physical properties are also presented in Fig. 1 and Table 1, respectively. Additionally, tap water was selected to mix the cement, fiber, and tailings.

Fig. 1 Particle size distribution of materials (Test instrument: MLS13320, Beckman, USA)
Table 1 Physical properties of materials (Test instrument: ZSX Primusll II, Rigaku Corporation, Japan)
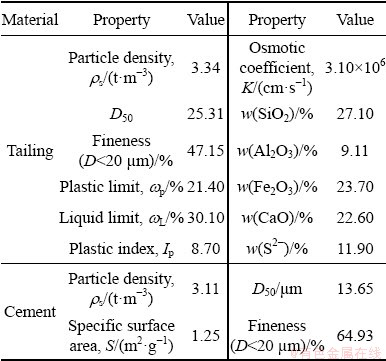
Fig. 2 XRD pattern of tailings (Test instrument: Ultima IV, Rigaku Corporation, Japan)
2.1.2 Polypropylene fiber
To improve the strength of fiber-reinforced CPB, polypropylene (PP) fiber was selected due to its high fracture strength and elastic modulus. The production technology of PP fibers is mature and the material source is wide. As shown in Fig. 3, the PP fiber used is white, short rod-shaped, and monofilament materials, and the SEM image shows that it has a smooth surface structure. The molecular formula of PP fiber is  , and carbon is the main ingredient of PP fiber, which is also tested by EDS. Moreover, PP fibers have good dispersion and can be evenly distributed in the slurry, which ensures that the fiber-added slurry still has good workability.
, and carbon is the main ingredient of PP fiber, which is also tested by EDS. Moreover, PP fibers have good dispersion and can be evenly distributed in the slurry, which ensures that the fiber-added slurry still has good workability.

Fig. 3 Monofilament polypropylene fiber (a), its test results of SEM (b) and EDS (c) (The fiber was treated by spray-gold, which led to high gold content in EDS tests)
2.2 UCS dataset preparation
A large number of UCS experiments were performed to develop the strength evaluation database in this study. Firstly, the CPB raw materials including tailings, PP fibers, cement, and water, were mixed in a mortar mixer for approximately 10 min to produce the fresh slurry. Then, the slurry was poured into cylindrical plastic molds with 50 mm in diameter and 100 mm in height, and the specimens were cured in a curing box with a temperature of (22±1) °C and a relative humidity of 90%. In this work, PP fiber was used as the CPB additive material, and the effects of fiber content and fiber length on the compressive strength were taken as the key research contents. Additionally, the influences of cement-to-tailing mass ratio, solid mass concentration, and curing time on the compressive strength were studied in this work because these factors have been illustrated to have an obvious effect on the strength of fiber-reinforced CPB [15-17]. Therefore, based on engineering experience and trial tests, different levels of these five factors were chosen according to the following scheme. Cement-to-tailing mass ratio: 1:4, 1:5, 1:6, 1:7, 1:8, 1:10, 1:12, and 1:14; solid mass concentration: 56, 58, 60, 62, 64, and 66 wt.%; curing time: 3, 7, 28, and 56 d; fiber content: 0, 0.5, 1.0, 1.5, 2.0, 3.0, and 4.0 kg/m3; fiber length: 3, 6, 9, and 12 mm. Three replicates of each CPB material proportion and a total of 720 CPB specimens were prepared, and the mean UCS values were used as the dataset for intelligent prediction. When the CPB was cured to the required ages, the UCS of the CPB was tested by a computer-controlled fully automatic pressure testing machine with a constant displacement rate of 0.2 mm/min. As shown in Fig. 4, the input variable dataset, distribution, and box plots are plotted, and it is easy to find that there are some outliers in the box plot. For the convenience of calculation, the cement-to-tailing mass ratio values in Fig. 4 are converted into percentage values, which are 25%, 20%, 17%, 14%, 13%, 10%, 8% and 7%, respectively.
3 Intelligent techniques
3.1 Artificial neural network
As an important part of AI technology, artificial neural network (ANN) was inspired by human brain calculations and proposed by MCCULLOCH and PITTS in 1943 [31]. The ANN model was developed by using the training datasets, and then the experience learned from the training datasets was utilized to predict the testing datasets. An ANN model includes layers (input, hidden, and output layers) and neurons in these layers. After continuous research, some linking methods for connecting the neurons were proposed. Among these methods, the feed-forward back propagation (BP) is a typical procedure and has been widely applied in many areas [32]. Therefore, this method was selected to predict the UCS of CPB in this study. Limited by the article length, some introduction about the ANN model was not shown here, readers can found them in the previous study [33].
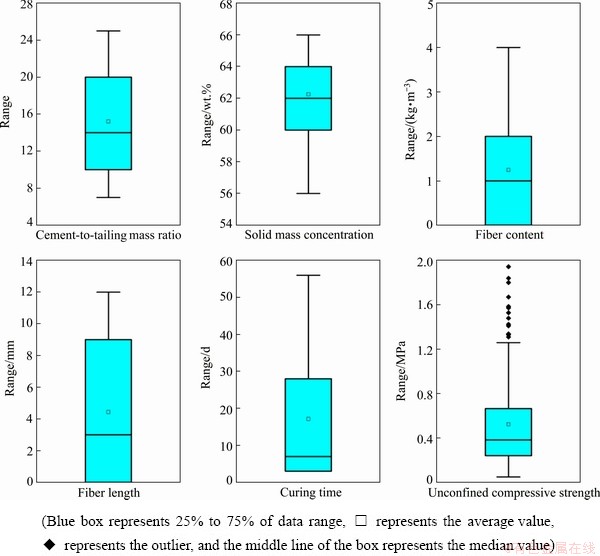
Fig. 4 Box plots of strength evaluation database
3.2 Support vector regression
Similar to ANNs, support vector machine (SVM) is also an important branch of AI technology [34]. This technology can be used to solve the regression problem and the classification problem, hence SVM can be divided into support vector regression (SVR) and support vector classification (SVC) according to the function of regression and classification. After reviewing previous studies, support vector regression has been utilized to predict the blast-induced rock movement [35,36], rockburst [37], the advance rate of a tunnel boring machine [38], the complicated flow behavior of alloys [39], and the rock fragmentation [40] with high prediction precision. Therefore, an SVR model was developed in this work and utilized to predict the UCS of CPB samples. For regression proposes, the Gaussian radial basis kernel function (RBF) verified by CHANG and LIN [41] was selected to transform the input datasets into a high-dimensional feature space.
3.3 Extreme learning machine
Extreme learning machine (ELM) is a famous feed-forward neural network algorithm and only one hidden layer can be found in this algorithm [42] (see Fig. 5). Compared to the traditional learning algorithm, the ELM can yield good generalization performance with less calculation time [43,44]. In this algorithm, the input weights and bias of hidden nodes were selected automatically using random methods, and only the output weights needed to be determined first [45].
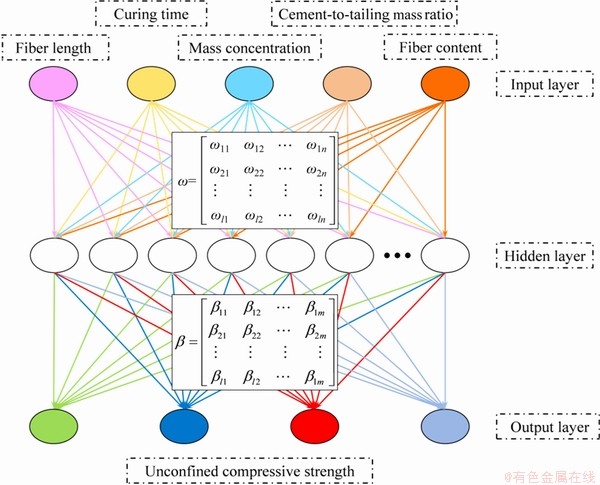
Fig. 5 ELM model structure
Using the input matrix X, output matrix Y, and neuron activation function g(x), the prediction results of input variable T can be expressed as follows [43]:
 (1)
(1)
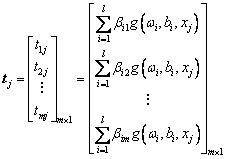 (2)
(2)
where ti is the ith predicted result; m is the number of output variables; Q is the number of samples; ωi is the weight between the ith input layer and hidden layer; bi is the bias of the hidden layer; and βi is the weight between the hidden layer and output layer; xj is the value of jth sample.
The prediction performance is the best when 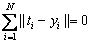 , where yi is actual value of the output variable for ith sample, which means that the ELM model can perfectly predict the training sample. The above equation can be transformed into the following equation by using a hidden layer output matrix H [42]:
, where yi is actual value of the output variable for ith sample, which means that the ELM model can perfectly predict the training sample. The above equation can be transformed into the following equation by using a hidden layer output matrix H [42]:
Hβ=T′ (3)
To calculate the bias matrix of hidden layer neurons b and the matrix of the input weights ω and β can be found by using a least-square process [42]:
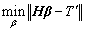 (4)
(4)
The result of the above equation is as follows:
β=H+T (5)
where H+ is the generalized Moore-Penrose inverse of H matrix.
3.4 Salp swarm algorithm
Salps are barrel-shaped, gelatinous zooplankton and regularly from large swarms (see Fig. 6). New research shows that salp plays a key role in marine food webs as the food source of many marine species [46]. Similar to jellyfish, salp moves by spraying water from the body [47]. There is a special behavior of salps in the deep ocean: the salp always comes from a swarm called the salp chain, and the leader salp in the salp chain can help the salp chain find the food source [48].
Fig. 6 Swarm behavior of slaps in deep ocean
Inspired by the natural behavior of salp swarms, the salp swarm algorithm was proposed by MIRJALILI et al [49] in 2017. In this model, salps in the salp chains were divided into two groups: leader salp and follower salps. The leader salp has the responsibility to guide the salp chains, and the follower salps will follow the leader salp during the moving process.
When that algorithm was utilized in solving optimization problems, the position of the food source means the optimal results of the problem, and the optimization performance is the best when the position of the food source matches the position of the leader salp.
The position of the leader salp can be obtained by using the following equation [49]:
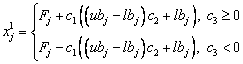 (6)
(6)
where 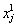 is the coordinate of leader salp; Fj is the position of the food resource; ubj and lbj are the upper bound and lower bound of the jth dimension, respectively; c1 is the parameter that can be used to balance the exploration and exploitation process; c2 and c3 are random numbers.
is the coordinate of leader salp; Fj is the position of the food resource; ubj and lbj are the upper bound and lower bound of the jth dimension, respectively; c1 is the parameter that can be used to balance the exploration and exploitation process; c2 and c3 are random numbers.
The position of the following salps in the salp chain can be expressed as follows:
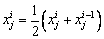 (7)
(7)
where i is the number greater than or equal to 2 and 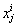 describes the position of the ith salp in dimension j. Equation (7) shows an iterative process for the calculation of
describes the position of the ith salp in dimension j. Equation (7) shows an iterative process for the calculation of 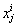 , and
, and 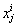 will be updated by averaging the values of
will be updated by averaging the values of 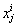 and
and 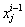 obtained in the above step.
obtained in the above step.
3.5 SSA-ELM model
The calculation procedure of the SSA-ELM model can be divided into the following six steps (Fig. 7).
(1) Establish the uniaxial compressive strength (UCS) database, which considers 5 input variables (cement-to-tailing mass ratio, solid mass concentration, fiber content, fiber length, curing time) and 1 output variable.
(2) Scale the input variables and output variable into -1 to 1.
(3) Randomly divide the database into training datasets and testing datasets with ratios of 80% and 20%, respectively [50].
(4) Use the SSA algorithm to select the optimal combination of weight values.
(5) Develop the optimal ELM model by using the optimal weight values.
(6) Predict the testing datasets and evaluate the prediction performance by using the correlation coefficient (R), root mean square error (RMSE), and variance account for (VAF).
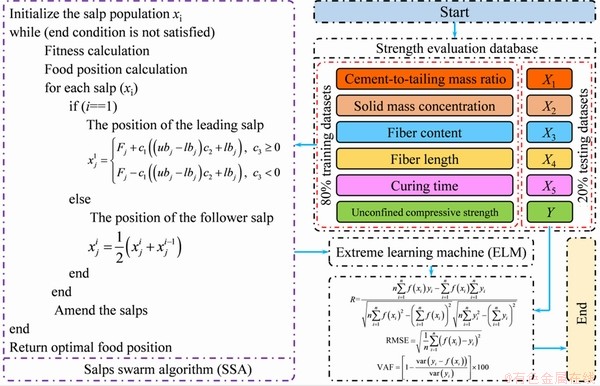
Fig. 7 Flowchart of SSA-ELM model
4 Results of intelligent models prediction
4.1 Performance metrics
To describe the prediction performance of the ANN model, SVR model, ELM model, and SSA-ELM model, three performance metrics including R, RMSE and VAF were selected in this work after reviewing the research of YU et al [51], ZHOU [52,53] and QI et al [54].
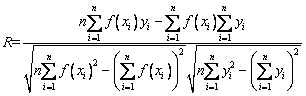 (8)
(8)
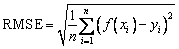 (9)
(9)
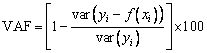 (10)
(10)
where n is the number of input datasets; yi is the ith actual UCS value; f(xi) is the ith predicted UCS value. For these prediction models, the prediction performance is the best when the RMSE, R, and VAF are 0, 1 and 100, respectively.
4.2 Predictive performance of ANN model
For predicting the UCS by using the ANN model, the number of hidden layers and the number of neurons (NON) in the hidden layer should be investigated first. So, a parameter investigation was carried out. Some previous studies [55-57] show that an ANN model with only one hidden layer can solve most of the engineering problems in many areas, and the ANN model with more hidden layers can be utilized in more complex issues. As suggested by HECHT-NIELSEN [58], NON should not exceed 2 times the input variables plus 1. Therefore, various ANN models with the number of hidden layers from 1 to 3 and the number of hidden neurons from 1 to 11 were developed and run 5 times to select the optimal value of the NON. During this process, the 10-fold cross-validation method was applied to evaluating the generalization performance and guiding the optimal ANN model selection. Then, the optimal number of hidden layers was found to be 3, and the number of hidden neurons of each hidden layer was 4, 10 and 8, respectively. After optimal ANN model development, the ANN model yielded a prediction performance of R=0.9286, RMSE=0.1486, and VAF=86.1491 for training datasets and R=0.9183, RMSE=0.1936, and VAF=83.6873 for testing datasets (see Fig. 8).
4.3 Predictive performance of SVR model
In the SVR model, the combination of two hyperparameters, including the penalty factor (C) and gamma in the RBF kernel (g), has a significant impact on the prediction performance. Hence, a grid-search method (GSM) was used to search for the optimal hyperparameter combination. In this work, 10.0 and -10.0 were selected as the upper and lower boundaries of the search scope, respectively. After searching, 1.5157 and 0.2500 were selected as the optimal values of C and g, and the optimal prediction performance was R=0.9163, RMSE=0.1664, and VAF=82.5737 for the training datasets and R=0.9138, RMSE=0.1936, and VAF=83.2272 for the testing datasets (see Fig. 9).
4.4 Predictive performance of ELM model
To develop the optimal ELM model, the number of hidden nodes should be investigated first. Hence, 200 ELM models with the number of hidden nodes from 1 to 200 were developed, run 5 times, and utilized to search for the optimal ELM model structure. Similar to the optimal ANN model selection process, the 10-fold cross-validation method was utilized to guide the optimal number of hidden nodes searching. As shown in Fig. 10, the minimum value of fitness was obtained when the number of hidden nodes was 36, so 36 was chosen after considering the generalization performance of the trained ELM model. Finally, the original ELM model has a prediction performance of R=0.9195, RMSE=0.1562, and VAF=84.5471 for training datasets, and R=0.9305, RMSE=0.1847, and VAF=85.6091 for the testing datasets (see Fig. 11).

Fig. 8 Predicted performance of ANN model
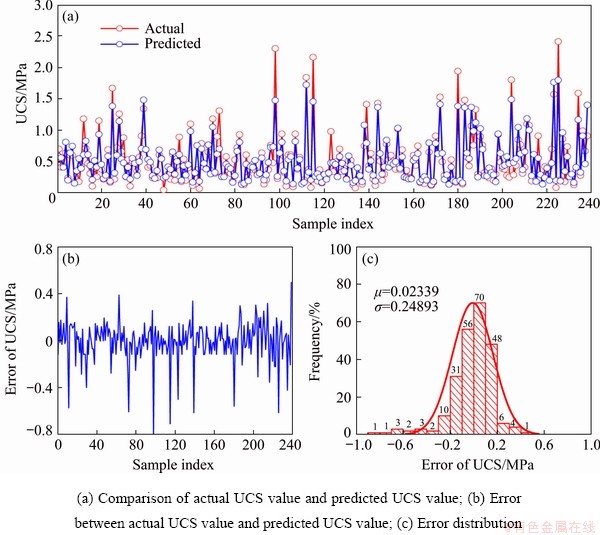
Fig. 9 Predicted performance of SVR model
4.5 Predictive performance of SSA-ELM model
In this study, the salp swarm algorithm (SSA) was used to select the optimal hyperparameters of the ELM model. Compared with the traditional ELM model, the SSA model can develop the ELM model with the optimal weight value rather than the randomly selected weight value. First, a parameter investigation of the hidden nodes in the hidden layer was conducted, and 200 ELM models with the number of hidden nodes from 1 to 200, number of salps in salp chain of 40 and maximum iteration of 400 were developed and run 5 times. The obtained results show that the optimal number of hidden nodes decreases from 36 to 14 after finding the optimal hyperparameters of the ELM model by using the 10-fold cross-validation method compared with the original ELM model as shown in Fig. 12.
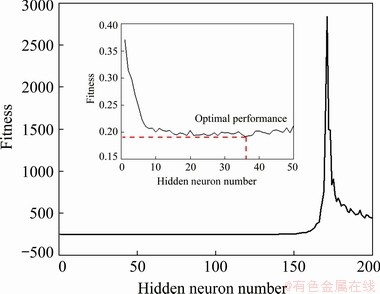
Fig. 10 Fitness of ELM model with various hidden nodes
To develop the optimal SSA-ELM model, the number of salps (NOS) in the salp chain and the maximum number of iterations should be investigated. Hence, a parameter study was carried out by establishing 9 SSA-ELM models with a maximum iteration of 1000 and NOS from 20 to 300 and running 5 times (see Fig. 13). As shown, there are no significant changes in these fitness curves after 800 iterations, and 150 was found to be the optimal NOS with the lowest RMSE value. However, the value of c1 is affected by the value of the maximum number of iterations, so 1000 and 150 were chosen to establish the final SSA-ELM model for predicting the UCS of CPB samples. After prediction, the R, RMSE, and VAF values of the training datasets were found to be 0.9392, 0.1364, and 88.2135, respectively, and the R, RMSE, and VAF values of the testing datasets were 0.9494, 0.1835, and 86.6022, respectively, for the best SSA-ELM model (see Fig. 14).
5 Discussion
5.1 Performance comparison
For the aims of performance comparison, the actual UCS, predicted UCS, the error of these two values are shown in Figs. 8, 9, 11 and 14. It is clear that the errors of the ANN, SVR, and ELM prediction results have a wider distribution range of -1.0 to 1.0, while the SSA-ELM model has a distribution range of -0.7 to 0.7. In addition to this phenomenon, the distribution parameter shows that the SSA-ELM has the minimum absolute value of center value (μ) and almost the minimum value of width value (σ), which means that the error of the actual value and the predicted value is smaller.
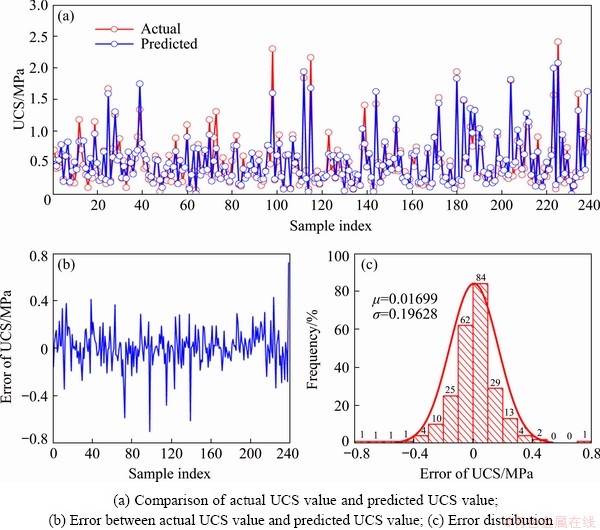
Fig. 11 Predicted performance of original ELM model
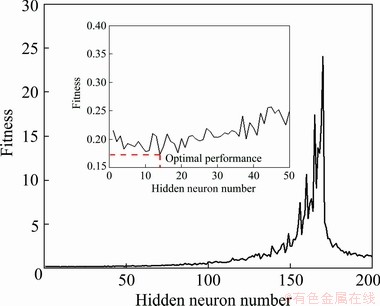
Fig. 12 Fitness of SSA-ELM model with various hidden nodes
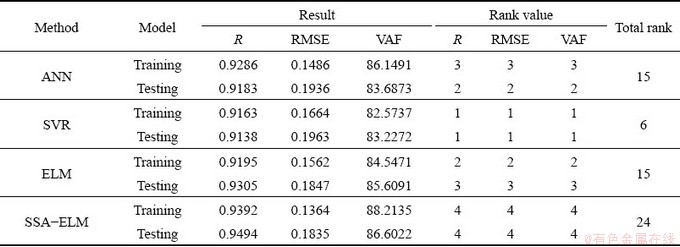
Moreover, a ranking method proposed by ZORLU et al [59] was utilized, as shown in Table 2. From the results of Table 2, the SSA-ELM model (R=0.9392, RMSE=0.1364, and VAF=88.2135 for training datasets, R=0.9494, RMSE=0.1835, and VAF=86.6022 for testing datasets, the total rank of 24) was found to be the most accurate prediction model.
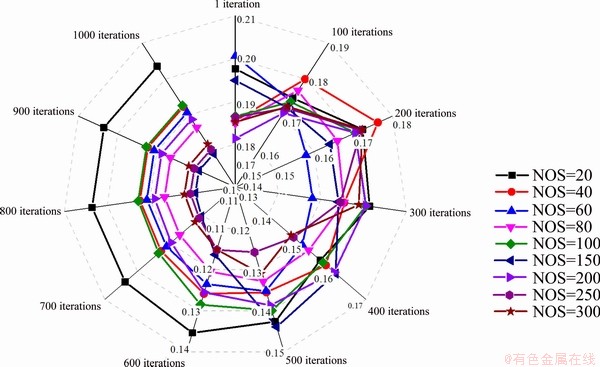
Fig. 13 Fitness curves of 9 SSA-ELM models with 1000 iterations and various number of salp (NOS) in salp chain
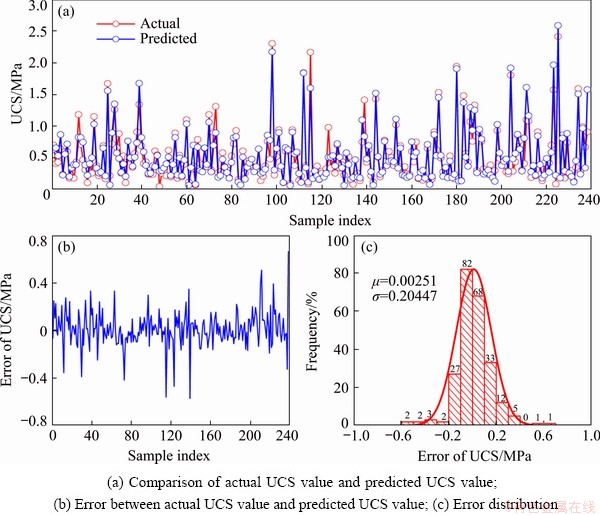
Fig. 14 Prediction performance of SSA-ELM model
Table 2 Performance indices of 4 prediction models
5.2 Sensitivity analysis
A sensitivity analysis was conducted in this work to analyze the relative importance of input variables for the UCS of fiber-reinforced CPB. For this aim, a simple but commonly used method, the cosine amplitude method [60], was utilized to evaluate the importance of each variable by using a value ranging from 0 to 1, where 0 means the least important and 1 means the most important. The results shown in Fig. 15 indicate that all influencing variables are important with a nonignorable importance score. The importance of the variables on the UCS increase is ranked as follows: cement-to-tailing mass ratio (CR, 0.9057) > solid mass concentration (SMC, 0.8604) > fiber content (FC, 0.7226) > fiber length (FL, 0.7051) > curing time (CT, 0.6989). The cement-to-tailing mass ratio and solid mass concentration are the main variables affecting the UCS of the CPB, which is common sense and agrees with the findings in previous studies [61,62]. Because sufficient tailings guarantee the formation of the CPB matrix, the hydration reaction of cement can effectively bind the loose tailings and lead to higher compressive strength of the CPB. In general, CPB prepared with higher cement-to-tailing mass ratio and solid mass concentration has a higher compressive strength [17]. Fiber can effectively affect the UCS of CPB, but it is not the critical variable compared to the cement-to-tailing mass ratio and solid mass concentration. Moreover, the effect of fiber content is more significant than that of fiber length. These conclusions have been reported in a previous study. Fiber can improve the UCS and toughness of CPB by its tensile properties, so that the integrity of CPB remains good after failure. The importance score of the curing time is 0.6989, which means that it is also a significant influencing variable for the UCS of the CPB. A large number of studies have shown that extending the curing time is conducive to the continuous improvement of the CPB strength [16,17]. However, it has also been reported that sulfur-containing tailings will restrict or even reduce the strength of CPB in the later stage of curing [7]. In addition, the obtained sensitivity analysis results are based on the developed strength evaluation database in this work, and more accurate sensitivity results can be found after enlarging the database.
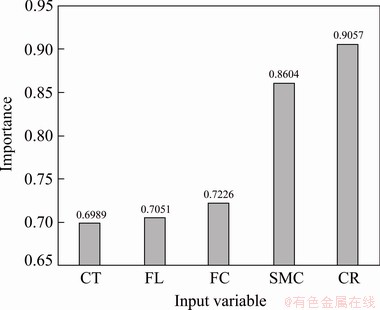
Fig. 15 Importance score of input variables
5.3 Superiority and limitations
After analysis, the proposed SSA-ELM model is an inexpensive, easy-to-use, high-precision and nondestructive method for the strength evaluation of fiber-reinforced CPB and can be utilized to guide fiber-reinforced CPB design in mining engineering. This study also helps to further understand the impact and importance of fiber on the strength of CPB, and the combined effects of fiber variables and conventional variables on the UCS of CPB. Compared to conventional mechanical tests, the UCS value of fiber-reinforced CPB material can be obtained by an accurate SSA-ELM model without unnecessary specimens, and UCS tests are required. Therefore, the proposed method in this work can significantly decrease the cost of CPB investigation. Additionally, the accuracy of the developed predictive model can be easily improved by enlarging the database. The procedure of developing a satisfactory SSA-ELM model has been described in detail in the present work, so it is much easier to develop a predictive model than to find a high-precision empirical equation for describing the relationship between the UCS value and influenced variables. Moreover, the SSA-ELM model is an open intelligent prediction model that can provide convenience for the prediction of the UCS of the CPB involving other fiber types and fiber variables in further research.
Although some achievements have been obtained in this study, all the variables affecting the UCS of CPB cannot be considered completely, and some limitations have also been found. The physical and chemical properties of tailings are considered to be able to significantly affect the strength of CPB, especially the particle size distribution. It is generally considered that tailings with a good grain size distribution are beneficial to improving the strength of CPB [63,64]. Moreover, the content of oxide in tailings also has a certain influence on the strength of backfill, and research shows that the silicon dioxide in tailings is good for the hydration reaction in CPB and further enhances the strength of CPB [5]. Taking the physical and chemical characteristics of tailings as variables, QI et al [25] established a UCS intelligent prediction model of CPB, and obtained good prediction accuracy. The existence of sulfate in tailings will reduce the strength of CPB because sulfate can undergo a chemical reaction in water, acidifying the slurry and forming sulfate radicals. Sulfate attacks can restrain C—S—H gelling generation and increase the secondary expandability production of ettringite and gypsum [65]. This kind of strength weakening usually occurs in the later stage of curing, because the hydration in CPB is almost finished at this stage, and the harm of sulfate erosion is gradually highlighted [66]. In addition, the hydration reaction in CPB is a process of quantitative and qualitative changes in active substances, and the change in curing temperature has a significant impact on the strength of the reaction. Studies have shown that as the curing temperature increases, the strength of CPB also increases [67]. Moreover, the curing time is also an important factor affecting the strength of CPB. It is also meaningful to study the strength characteristics of CPB after long-term curing [16]. In this study, the maximum curing time is only 56 d, which is not a complete analysis of the mechanical properties of fiber-reinforced CPB. Additionally, the pH values of the environment and more fiber variables, etc., also have an impact on the mechanical properties of fiber-reinforced CPB. Limited to the experiments, those variables were not considered in the CPB strength design and artificial intelligence model development. Therefore, more influential variables, such as particle size distribution, oxide content, sulfate content, curing temperature and pH, should be considered in the future investigation. Although SSA-ELM can provide the high-precision predictive performance of fiber-reinforced CPB strength evaluation, more artificial intelligence technologies such as random forest (RF), can be tried to solve this problem.
6 Conclusions
(1) A CPB database was established including 6 variables (fiber length, curing time, solid mass concentration, cement-to-tailing mass ratio, fiber content, and UCS) after 720 UCS tests. Among these variables, fiber length, curing time, solid mass concentration, cement-to-tailing mass ratio, and fiber content were inputted into the prediction model as the input variables, and UCS was outputted as the output variable.
(2) The SSA algorithm can significantly decrease the hidden neurons of the ELM model, which can effectively increase the calculation ability. Moreover, the prediction performance of ELM was improved after optimization by the SSA algorithm. Compared to the ANN, SVR, and ELM models, the SSA-ELM model can predict the UCS with higher prediction precision (R of 0.9392, RMSE of 0.1364, and VAF of 88.2135 for training datasets, R of 0.9494, RMSE of 0.1835, and VAF of 86.6022 for testing datasets).
(3) The sensitivity analysis indicates that the reinforcement effect of the fiber variables on the CPB strength is less significant than that of the cement-to-tailing mass ratio and solid mass concentration but more significant than that of the curing time. The importance scores of the fiber content and fiber length are 0.7226 and 0.7051, respectively.
(4) The SSA-ELM model is an inexpensive, easy-to-use, high-precision and nondestructive method for the strength evaluation of fiber-reinforced CPB and can be utilized to guide UCS design. This study also helps to further understand the combined effects of fiber variables and conventional variables on the UCS of CPB.
Acknowledgments
The authors are grateful for the financial supports from the National Natural Science Foundation of China (51874350, 41807259); the National Key Research and Development Program of China (2017YFC0602902); the Fundamental Research Funds for the Central Universities of Central South University of China (2018zzts217); the Innovation-Driven Project of Central South University of China (2020CX040).
References
[1] CHEN Qiu-song, ZHANG Qin-li, FOURIE A, CHEN Xin, QI Chong-chong. Experimental investigation on the strength characteristics of cement paste backfill in a similar stope model and its mechanism [J]. Construction and Building Materials, 2017, 154(15): 34-43.
[2] QI Chong-chong, FOURIE A. Cemented paste backfill for mineral tailings management: Review and future perspectives [J]. Minerals Engineering, 2019, 144: 106025.
[3] LIU Zhi-xiang, LAN Ming, XIAO Si-you, GUO Hu-qiang. Damage failure of cemented backfill and its reasonable match with rock mass [J]. Transactions of Nonferrous Metals Society of China, 2015, 25(3): 954-959.
[4] ZHANG Zong-guo, SHI Xiu-zhi, LIN Xue-fei. Parameter optimization and transportation characteristics of backfilling pipe network based on CFD [J]. The Chinese Journal of Nonferrous Metals, 2018, 29(10): 2411-2420. (in Chinese)
[5] CHEN Xin, SHI Xiu-zhi, ZHOU Jian, CHEN Qiu-song, LI En-ming, DU Xiang-hong. Compressive behavior and microstructural properties of tailings polypropylene fibre-reinforced cemented paste backfill [J]. Construction and Building Materials, 2018, 180: 211-221.
[6] CHEN Xin, SHI Xiu-zhi, ZHOU Jian, YU Zhi. Influence of polypropylene fiber reinforcement on tensile behavior and failure mode of tailings cemented paste backfill [J]. IEEE Access, 2019, 7: 69015-69026.
[7] CHEN Xin, SHI Xiu-zhi, ZHOU Jian, DU Xiang-hong, CHEN Qiu-song, QIU Xian-yang. Effect of overflow tailings properties on cemented paste backfill [J]. Journal of Environment Management, 2019, 235: 133-144.
[8] CHEN Qiu-song, SUN Shi-yuan, LIU Yi-kai, QI Chong- chong, ZHOU Hui-bo, ZHANG Qin-li. Experimental and numerical study on immobilization and leaching characteristics of fluoride from phosphogypsum based cemented paste backfill [J]. International Journal of Minerals Metallurgy and Materials, 2021. DOI: https://doi.org/ 10.1007/s12613-021-2274-6.
[9] KAYALI O, HAQUE M N, ZHU B. Some characteristics of high strength fiber reinforced lightweight aggregate concrete [J]. Cement and Concrete Composites, 2003, 25(2): 207-213.
[10] SONG P S, HWANG S. Mechanical properties of high- strength steel fiber-reinforced concrete [J]. Construction and Building Materials, 2004, 18: 669-673.
[11] ZHOU Ke-ping, BI Lin, LI Jie-lin, DENG Hong-wei, BIN Feng. Microscopic damage and dynamic mechanical properties of rock under freeze-thaw environment [J]. Transactions of Nonferrous Metals Society of China, 2015, 25(4): 1254-1261.
[12] YANG Yu-you, WANG Jian-qiang, DOU Hai-jun. Mechanical properties of anti-seepage grouting materials for heavy metal contaminated soil [J]. Transactions of Nonferrous Metals Society of China, 2014, 24(10): 3316-3323.
[13] ERCIKDI B, CIHANGIR F, KESIMAL A, DEVECI H, ALP I. Effect of natural pozzolans as mineral admixture on the performance of cemented-paste backfill of sulphide-rich tailings [J]. Waste Management and Research, 2010, 28(5): 430-435.
[14] KOOHESTANI B, KOUBAA A, BELEM T, BUSSIERE B, BOUZAHZAH H. Experimental investigation of mechanical and microstructural properties of cemented paste backfill containing maple-wood filler [J]. Construction and Building Materials, 2016, 121: 222-228.
[15] HE Yan, CHEN Qiu-song, QI Chong-chong, ZHANG Qin-li, XIAO Chong-chun. Lithium slag and fly ash-based binder for cemented fine tailings backfill [J]. Journal of Environment Management, 2019, 248: 109282.
[16] KESIMAL A, YILMAZ E, ERCIKDI B, ALP I, DEVECI H. Effect of properties of tailings and binder on the short-and long-term strength and stability of cemented paste backfill [J]. Materials Letters, 2005, 59(28): 3703-3709.
[17] DENG D Q, LIU L, YAO Z L, SONG K I I L, LAO D Z. A practice of ultra-fine tailings disposal as filling material in a gold mine [J]. Journal of Environment Management, 2017, 196: 100-109.
[18] FALL M, BENZAAZOUA M, OUELLET S. Experimental characterization of the influence of tailings fineness and density on the quality of cemented paste backfill [J]. Minerals Engineering, 2005, 18(1): 41-44.
[19] HANE I, BELEM T, BENZAAZOUA M, MAQSOUD A. Laboratory characterization of cemented tailings paste containing crushed waste rocks for improved compressive strength development [J]. Geotechnical and Geological Engineering, 2017, 35: 645-662.
[20] CHEN Xin, SHI Xiu-zhi, ZHANG Shu, CHEN Hui, ZHOU Jian, YU Zhi, HUANG Pei-sheng. Fiber-reinforced cemented paste backfill: The effect of fiber on strength properties and estimation of strength using nonlinear models [J]. Materials, 2020, 13(3): 718.
[21] YILMAZ T, ERCIKDI B. Predicting the uniaxial compressive strength of cemented paste backfill from ultrasonic pulse velocity test [J]. Nondestructive Testing and Evaluation, 2016, 31(3): 247-266.
[22] ERCIKDI B, YILMAZ T, KULEKCI G. Strength and ultrasonic properties of cemented paste backfill [J]. Ultrasonics, 2014, 54(1): 195-204.
[23] XU Wen-bin, TIAN Xi-chun, CAO Pei-wang. Assessment of hydration process and mechanical properties of cemented paste backfill by electrical resistivity measurement [J]. Nondestructive Testing and Evaluation, 2018, 33(2): 198-212.
[24] OREJARENA L, FALL M. The use of artificial neural networks to predict the effect of sulphate attack on the strength of cemented paste backfill [J]. Bulletin of Engineering Geology and the Environment, 2010, 69(4): 659-670.
[25] QI Chong-chong, CHEN Qiu-song, FOURIE A, ZHANG Qin-li. An intelligent modelling framework for mechanical properties of cemented paste backfill [J]. Minerals Engineering, 2018, 123: 16-27.
[26] LU Xiang, ZHOU Wei, DING Xiao-hua, SHI Xu-yang, LUAN Bo-yu, LI Ming. Ensemble learning regression for estimating unconfined compressive strength of cemented paste backfill [J]. IEEE Access, 2019, 7: 72125-72133.
[27] QI Chong-chong, FOURIE A, CHEN Qiu-song. Neural network and particle swarm optimization for predicting the unconfined compressive strength of cemented paste backfill [J]. Construction and Building Materials, 2018, 159: 473-478.
[28] QI Chong-chong, FOURIE A, CHEN Qiu-song, TANG Xiao-lin, ZHANG Qin-li, GAO Ru-gao. Data-driven modelling of the flocculation process on mineral processing tailings treatment [J]. Journal of Cleaner Production, 2018, 196: 505-516.
[29] QI Chong-chong, CHEN Qiu-song, DONG Xiang-jian, ZHANG Qin-li, YASEEN Z M. Pressure drops of fresh cemented paste backfills through coupled test loop experiments and machine learning techniques [J]. Powder Technology, 2020, 361: 748-758.
[30] GB 175—2007. China’s Common Portland Cement Standard [S]. Beijing: China National Standardization Management Committee, 2007. (in Chinese)
[31] MCCULLOCH W S, PITTS W. A logical calculus of the ideas immanent in nervous activity [J]. The Bulletin of Mathematical Biophysics, 1943, 5: 115-133.
[32] ZHOU Jian, KOOPIALIPOOR M, LI En-ming, ARMAGHANI D J. Prediction of rockburst risk in underground projects developing a neuro-bee intelligent system [J]. Bulletin of Engineering Geology and the Environment, 2020, 79(8): 4265-4279.
[33] SCHALKOFF R . Artificial neural networks (Vol.1) [M]. New York: McGraw-Hill, 1997.
[34] VAPNIK V. The nature of statistical learning theory [M]. New York: Springer, 1995.
[35] YU Zhi, SHI Xiu-zhi, ZHOU Jian, RAO Di-jun, CHEN Xin, DONG Wen-ming, MIAO Xiao-hu, IPANGELWA T. Feasibility of the indirect determination of blast-induced rock movement based on three new hybrid intelligent models [J]. Engineering with Computers, 2021, 37: 991-1006.
[36] YU Zhi, SHI Xiu-zhi, ZHOU Jian, CHEN Xin, MIAO Xiao-hu, TENG Bing, IPANGELWA T. Prediction of blast-induced rock movement during bench blasting: Use of gray wolf optimizer and support vector regression [J]. Natural Resources Research, 2020, 29: 843-865.
[37] ZHOU Jian, LI Xi-bing, MITRI S H. Evaluation method of rockburst: State-of-the-art literature review [J]. Tunnelling and Underground Space Technology, 2018, 81: 632-659.
[38] ZHOU Jian, QIU Yin-gui, ZHU Shuang-li, ARMAGHANI D J, LI Chuan-qi, NGUYEN H, YAGIZ S. Optimization of support vector machine through the use of metaheuristic algorithms in forecasting TBM advance rate [J]. Engineering Applications of Artificial Intelligence, 2021, 97: 104015.
[39] SHI Ze-yan, QUAN Guo-zheng, AN Chao, QIU Wei-yong, ZHANG Zhi-hua. Artificial intelligence model of complicated flow behaviors for Ti-13Nb-13Zr alloy and relevant applications [J]. Transactions of Nonferrous Metals Society of China, 2019, 29(10): 2090-2098.
[40] SHI Xiu-zhi, ZHOU Jian, WU Bang-biao, HUANG Dan, WEI Wei. Support vector machines approach to mean particle size of rock fragmentation due to bench blasting prediction [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(2): 432-441.
[41] CHANG C, LIN C J. LIBSVM: A library for support vector machines [M]. New York: ACM, 2011.
[42] HUANG Guang-bin, ZHU Qin-yu, SIEW C K. Extreme learning machine: Theory and applications [J]. Neurocomputing, 2006, 70(1-3): 489-501.
[43] GAO Jiu-wen, ZHANG Kai, LUO Min-xia, YIN Chun, LAI Xiao-ping. Extreme learning machine and adaptive sparse representation for image classification [J]. Neural Networks, 2016, 81: 91-102.
[44] CHATURVEDI I, RAGUSA E, GASTALDO P, ZUNINO R, CAMBRIA E. Bayesian network based extreme learning machine for subjectivity detection [J]. Journal of the Franklin Institute, 2018, 335(4): 1780-1797.
[45] ZENG Nian-yin, ZHANG Hong, LIU Wei-bo, LIANG Jin-ling, ALSAADI F E. A switching delayed PSO optimized extreme learning machine for short-term load forecasting [J]. Neurocomputing, 2017, 240: 175-182.
[46] HENSCHKE N, EVERETT J D, RICHARDSON A J, SUTHERS L M. Rethinking the role of salps in the ocean [J]. Trends in Ecology and Evolution, 2016, 31(9): 720-733.
[47] MADIN L P. Aspects of jet propulsion in salps [J]. Canadian Journal of Zoology, 1990, 68(4): 765-777.
[48] ANDERSON P A V, BONE Q. Communication between individuals in salp chains. II. Physiology [J]. Proceedings of the Royal Society of London (Series B): Biological Sciences, The Royal Society, 1980, 210(1181): 559-574.
[49] MIRJALILI S, GANDOMI A H, MIRJALILI S Z, SAREMI S, FARIS H, MIRJALILI S M. Salp swarm algorithm: A bio-inspired optimizer for engineering design problems [J]. Advances in Engineering Software, 2017, 114: 163-191.
[50] ARMAGHANI D J, SAFARI V, FAHIMIFAR A, AMIN M F M, MONJEZI M, MOHAMMADI M A. Uniaxial compressive strength prediction through a new technique based on gene expression programming [J]. Neural Computing and Applications, 2018, 30(11): 3523-3532.
[51] YU Zhi, SHI Xiu-zhi, ZHOU Jian, CHEN Xin, QIU Xian-yang. Effective assessment of blast-induced ground vibration using an optimized random forest model based on a harris hawks optimization algorithm [J]. Applied Sciences, 2020, 10(4): 1403.
[52] ZHOU Jian, QIU Yin-gui, ARMAGHANI D J, ZHANG Wen-gang, LI Chuan-qi, ZHU Shuang-li, TARINEJAD R. Predicting TBM penetration rate in hard rock condition: A comparative study among six XGB-based metaheuristic techniques [J]. Geoscience Frontiers, 2020, 12(3): 101091.
[53] ZHANG Hong, ZHOU Jian, ARMAGHANI D J, TAHIR M M, PHAM B T, HUYNH V V. A combination of feature selection and random forest techniques to solve a problem related to blast-induced ground vibration [J]. Applied Sciences, 2020, 10(3): 869.
[54] QI Chong-chong, CHEN Qiu-song, KIM S S. Integrated and intelligent design framework for cemented paste backfill: A combination of robust machine learning modelling and multi-objective optimization [J]. Minerals Engineering, 2020, 155: 106422.
[55] MOHAMAD E T, ARMAGHANI D J, MOMENI E, ABAD S V A N K. Prediction of the unconfined compressive strength of soft rocks: A PSO-based ANN approach [J]. Bulletin of Engineering Geology and the Environment, 2015, 74(3): 745-757.
[56] NGUYEN H, BUI X N, BUI H B, MAI N L. A comparative study of artificial neural networks in predicting blast-induced air-blast overpressure at Deo Nai open-pit coal mine, Vietnam [J]. Neural Computing and Applications, 2120, 32(8): 3939-3955.
[57] NGUYEN H, DREBENSTEDT C, BUI X N, BUI D T. Prediction of blast-induced ground vibration in an open-pit mine by a novel hybrid model based on clustering and artificial neural network [J]. Natural Resources Research, 2020, 29(2): 691-709.
[58] HECHT-NIELSEN R. Kolmogorov’s mapping neural network existence theorem [C]//Proceedings of the International Conference on Neural Networks. New York, 1987: 11-14.
[59] ZORLU K, GOKCEOGLU C, OCAKOGLU F, NEFESLIOGLU H A, ACIKALIN S. Prediction of uniaxial compressive strength of sandstones using petrography-based models [J]. Engineering Geology, 2008, 96(3-4): 141-158.
[60] YANG Y, ZHANG Q. A hierarchical analysis for rock engineering using artificial neural networks [J]. Rock Mechanics and Rock Engineering, 1997, 30(4): 207-222.
[61] FALL M, BENZAAZOUA M, SAA E G. Mix proportioning of underground cemented tailings backfill [J]. 2008, 23(1): 80-90.
[62] AMARATUNGA L M, YASCHYSHYN D N. Development of a high modulus paste fill using fine gold mill tailings [J]. Geotechnical and Geological Engineering, 1997, 15(3): 205-219.
[63] WANG Dao-lin, ZHANG Qin-li, CHEN Qiu-song, FENG Yan, XIAO Chong-chun. Temperature variation characteristics in flocculation settlement of tailings and its mechanism [J]. International Journal of Minerals, Metallurgy and Materials, 2020, 27(11): 1438-1448.
[64] CHEN Xin, SHI Xiu-zhi, ZHOU Jian, YU Zhi, HUANG Pei-sheng. Determination of mechanical, flowability, and microstructural properties of cemented tailings backfill containing rice straw [J]. Construction and Building Materials, 2020, 246: 118520.
[65] ERCIKDI B, CIHANGIR F, KESIMAL A, DEVECI H, ALP I. Utilization of industrial waste products as pozzolanic material in cemented paste backfill of high sulphide mill tailings [J]. Journal of Hazardous Materials, 2009, 168(2-3): 848-856.
[66] ERCIKDI B, BAKI H, IZKI M. Effect of desliming of sulphide-rich mill tailings on the long-term strength of cemented paste back fill [J]. Journal of Environment Management, 2013, 115: 5-13.
[67] FALL M, CELESTIN J C, POKHAREL M, TOURE M. A contribution to understanding the effects of curing temperature on the mechanical properties of mine cemented tailings back fill [J]. Engineering Geology, 2010, 114(3-4): 397-413.
喻 智, 史秀志, 陈 新, 周 健, 齐冲冲, 陈秋松, 饶帝军
中南大学 资源与安全工程学院,长沙 410083
摘 要:为降低纤维尾砂胶结充填材料单轴压缩强度数据的获取难度,综合分析常规充填材料参数与纤维参数对其单轴压缩性能的影响,结合元启发式算法(樽海鞘算法, SSA)与极限学习机技术(ELM),提出一种新型人工智能模型(SSA-ELM)。为检验模型可靠性,开展720组不同灰砂质量比、固体质量浓度、纤维含量、纤维长度和养护时间的纤维尾砂胶结充填材料单轴抗压实验以建立充填材料强度性能数据库。研究结果表明,训练好的SSA-ELM模型能够准确地预测纤维尾砂胶结充填材料的单轴压缩强度,其性能优于ANN、SVR和ELM方法;纤维含量和纤维长度对纤维尾砂胶结充填材料单轴压缩性能具有重要影响。
关键词:纤维尾砂胶结充填材料;单轴抗压强度;预测;极限学习机;樽海鞘算法
(Edited by Wei-ping CHEN)
Corresponding author: Xin CHEN; Tel: +86-15116336263; E-mail: chenxin_ck@csu.edu.cn
DOI: 10.1016/S1003-6326(21)65563-2
1003-6326/ 2021 The Nonferrous Metals Society of China. Published by Elsevier Ltd & Science Press
2021 The Nonferrous Metals Society of China. Published by Elsevier Ltd & Science Press

