J. Cent. South Univ. (2012) 19: 1615-1621

DOI: 10.1007/s11771-012-1184-1

Simulation of liquid-gas flow in

full-scale Caroussel oxidation ditch with surface aeration

LI Zhen-liang(李振亮)^1,2, GUO Li-sha(郭丽莎)³, ZHANG Dai-jun(张代钧)^{1, 4}, XU Dan-yu(许丹语)⁵

1. Department of Environmental Science, Chongqing University, Chongqing 400030, China;

2. Chongqing Education College, Chongqing 400067, China;

3. Department of Civil Engineering, Laval University, Québec G1V0A6, Canada;

4. Key Laboratory for the Resources Exploitation and Environmental Disaster Control Engineering in

Southwest China (Chongqing University), Ministry of Education, Chongqing 400030, China;

5. Tianjin Academy of Environmental Science, Tianjin 300191, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: A model for liquid-gas flow (MLGF), considering the free movement of liquid surface, was built to simulate the wastewater velocity field and gas distribution in a full-scale Caroussel oxidation ditch with surface aeration. It was calibrated and validated by field measurement data, and the calibrated parameters and sections were selected based on both model analysis and numerical computation. The simulated velocities of MLGF were compared to that of a model for wastewater-sludge flow (MWSF). The results show that the free liquid surface considered in MLGF improves the simulated velocity results of upper layer and surface. Moreover, distribution of gas volume fraction (GVF) simulated by MLGF was compared to dissolved oxygen (DO) measured in the oxidation ditch. It is shown that DO distribution is affected by many factors besides GVF distribution.

Key words: liquid-gas flow; computational fluid dynamics technique; oxidation ditch; surface free movement; gas volume fraction

1 Introduction

Dissolved oxygen (DO) distribution is a basis for modeling pollutant concentration fields and it is often related with velocity field and gas transfer. Usually, the gas transfer coefficient is described by Fick’s laws of diffusion which is tightly relevant with gas volume fraction (GVF) of oxygen [1]. Essentially, distribution of GVF is a source term when DO is computed. It could be treated as the distribution of oxygen when the wastewater is assumed to be pure water which means that no bioreations happen to consume or generate DO. Thus, a model for liquid-gas flow (MLGF) to simulate velocity field and gas distribution is very important and plays a fundamental roll in modelling DO distributions when taking bioreactions into account.

Computational fluid dynamics (CFD) is a useful tool to simulate and optimize reactors and there are various multiphase models. The models often used for liquid-gas flow simulation include volume of fraction (VOF) model, mixture model and Eulerian model [2]. VOF model was mainly suitable for modeling stratified flow and free-surface flow. Furthermore, mixture model developed from VOF model is available by defining a slip velocity to interpret the different flow velocities of different phases. Eulerian model is a more comprehensive model than the former two, and it needs to solve a set of conversation equations for each phase. The usage of Eulerian model relies on a clear grasp to movement rules among phases, e.g. the drag   coefficient [2].

Simulation for liquid-gas two-phase flow was wildly discussed in the field of bubble columns and deep aeration reactors [3-7], and the models were usually derived from Eulerian models, including Euler/Euler and Euler/Lagrange methods. In some Eulerian models of bubble columns and deep aeration reactors, the top surface was treated as a degasification condition which meant that merely gas can cross the top surface. This method is an excellent idea for those kinds of reactors, since the primary sources of oxygen are bubbles which float from bottom to top. However, it is not applicable for an oxygen ditch equipped with surface aerators because the oxygen is mainly introduced by liquid spray generated by rotation of aerator blades and is transferred from upper level to lower level. Besides, the degassing surface belongs to mobile wall condition, meaning that the surface is simplified as a solid mobile horizontal plane which can not be penetrated and its vertical movement is neglected. MOULLEC et al [4] reported that the mobile-wall surface will cause modeling errors at the surface and near areas. So, it is significant to model the free movement of liquid surface for an oxidation ditch with surface aeration.

In this work, wastewater and sludge were treated as a single liquid phase, named wastewater, and a model for liquid-gas flow (MLGF), considering the free movement of liquid surface, was built to simulate the wastewater velocity field and gas distribution in a full-scale Caroussel oxidation ditch with surface aeration. The simulated velocities were compared with the simulation results of the model for wastewater-sludge flow (MWSF) which adopted the mobile-wall surface and treated wastewater and sludge as two phases, separating their movements in vertical directions.

2 Experimental

2.1 Basic model

For those reactors like bubble columns and deep aeration reactors, gas transfer is mainly depended on bubbles whose movement rules and drag coefficient in the liquid have obtained deep investigations [8-11]. However, the drag coefficient of gas is seldom investigated for a full-scale oxygen ditch, especially for those which are equipped with surface aerators. So, Eulerian models are not suitable for the studied oxidation ditch in this work. Meanwhile, VOF cannot separate velocity field of liquid from gas which is a focus of this work. Thus, mixture model was selected as the basic model of MLGF and body force, and gravity and aeration were taken into account. In order to simulate the free movement of liquid surface, a gas layer was added above a wastewater layer, so the surface of wastewater layer could wave in vertical direction, not being a horizontal plane as in MWSF (described in detail in  Ref. [12]).

Continuity equation:

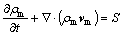                         (1)

Momentum conversation:

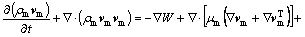
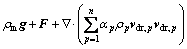          (2)

Turbulence models

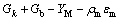                  (3)

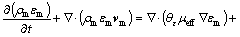
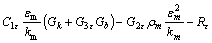       (4)

Volume fraction function of the second-phase flow:

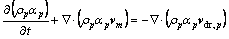        (5)

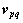where is connected with  through a function provided by software FLUENT 6.1.

Slip velocity:

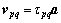                                  (6)

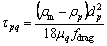                           (7)

where the slip velocity 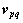 used in MWSF is the sludge settling velocity function [13].

2.2 Virtual model

The virtual geometrical model was built, as shown in Fig. 1, according to a full-scale Caroussel oxidation ditch of Fendu wastewater treatment plant (WWTP), Chongqing, China. There are four main straight ditches, each with a length of 61.7 m, a width of 3.5 m and an effective depth of 3.5 m. The virtual model of the oxidation ditch has a total height of 5 m, including a  3.5 m-high wastewater layer and a 1.5 m-high gas layer, each layer with an individual inlet.

Fig. 1 Geometrical model of oxidation ditch used in MLGF

Three surface aerators of down-umbrella type and two underwater low-speed impellers are located in the oxidation ditch. The diameter of aerators is 3.25 m, rotational speed is 32 r/min and aeration rate is 71-  107 kg(O₂)/h. Aerator R1 rotates clockwise while R2 and R3 rotate counterclockwise. The diameter of underwater impellers is 2.5 m, and the rotational speed is 42 r/min. Aerator R1 and R2 work all day but R3 adopts an alternate aeration, that is, R3 rests from 00:00 to 12:00 and then operates in an interval of 30 min from 12:00 to 24:00 every day. When the oxidation ditch is in an alternate aeration, the flow in gas layer changes furiously and is hard to be predicted, so this work only focused on the modeling under the comparatively stable flow field when R3 stops from 00:00 to 12:00.

Considering that the complicate structure of aerators and impellers would cause a lot of trouble for geometrical construction and numerical computation of model and since the modeling was focused on the stable situation, the surface aerators and underwater impellers were simplified respectively to truncated cones and thin columns.

The mesh of the studied oxidation ditch was also generated on GAMBIT, and in order to guarantee both computational accuracy and efficiency, different types of grids were used for different regions. The details of grids are listed in Table 1, and the total grid-element number of the whole model is counted to be 125 629.

Table 1 Grid element types of different areas in oxidation ditch

2.3 Boundary conditions

Once the model frame was illustrated and its mesh was output, the numerical computation of the model was carried out on FLUENT 6.3. The boundary conditions were defined as follows. Wastewater inlet was a “velocity-input” boundary whose influent velocity was 0.3 m/s and turbulence intensity was 0.04; gas inlet was also described as a “velocity-input” boundary with a velocity of 0.3 m/s and turbulence intensity of 1 (the default value of software); the type of outlet boundary was “outflow”; the top surface of gas layer was “pressure-input”; the aerators and impeller were defined by multiple frame of reference method, so the aerator/impeller was stationary relative to a rotating frame of reference which rotated at a speed of 3.3 rad/s for aerators and 4.4 rad/s for impeller; it was also important to set a y-direction velocity for the wastewater flow wrapping the underwater impellers, because the major function of impellers was to push the fluid to move along the direction of mainstream parallel to y axis in ditch N1 and N2 (Fig. 2), and the value for primary calculation was 0.5 m/s. Both body force and gravity were considered in the model. “Body force weighted” scheme was chosen for pressure interpolation, and “Simple” algorithm was chosen for pressure-velocity coupling.

2.4 Field measurement

Field measurement was done in Fendu WWTP to get necessary data for model calibration and validation. Fifteen monitor sections for velocity measurement were placed, as shown in Fig. 2. Except section S4 which had two monitor lines, others had five lines. Seven monitor points distributed evenly on each line, with an interval of 0.5 m.

Fig. 2 Oxidation ditch and its monitoring sections for velocity measurement

2.5 Model calibration

The model was calibrated by generalized likelihood uncertainty estimation (GLUE) with sampling method of Latin hypercube sampling (LHS). The parameters for model calibration were chosen mainly based on model analysis. The boundary conditions of inlets would affect the simulated velocity results. For the wastewater inlet, the influent velocity was measured in field but its turbulence intensity was not measured, so the turbulence intensity at wastewater inlet, I_w, needed calibration. For gas inlet, both influent velocity and turbulence intensity were unknown, but after several times of computation and comparison, it was discovered that the turbulence intensity had a more significant influence on the wastewater flow field, so the flow turbulence intensity at gas inlet, I_g, was also selected as a parameter for calibration. It was necessary to calibrate relevant parameters of aerator and impeller, because their structure and shape in the model were greatly simplified compared with the real entities. The aerators and impellers mainly made their effects on the fields through rotating and pushing fluid. Thus, rotational speed of aerator, r_a, was calibrated. However, for the impellers, the calibrated parameter was the y-direction velocity of the fluid surrounding the impeller, u_i, but not the rotational speed, because different from the aerators which influenced flow field by rotation, the primary function of impeller was to push the fluid forward. In sum, the calibration parameter subset was {I_w, I_g, r_a, u_i}.

3 Results and discussion

3.1 Results

The wastewater flow field under the stable condition when only R1 and R2 aerated was simulated by MLGF, and the results were compared with those simulated by MWSF. Figure 3 compares the average simulated velocities with the measured ones, and Table 2 lists the simulated errors. For S4, the average velocity of middle line, either simulated one or measured one, meant the average values of points on two monitor lines, while for the rest sections, the average velocity was the average of the middle monitor line.

It is shown, in Fig. 3 and Table 2, that the two models, MLGF and MWSF, yielded similar simulated errors with each other for the velocities on lower or middle layer, but for these on upper layer and top surface of wastewater flow, MLGF showed an obviously better result than MWSF. This might be due to the fact that the MLGF allowed the free movement of wastewater top surface, while MWSF treated the surface as a horizontal plane. The MLGF described the surface in a more accurate way and thus led to smaller errors. It should be noted that the velocimeter used in the field measurement could not distinguish the wastewater from sludge. Thus, the measured values and simulated values of MSWF were velocities of a mixture which combined both wastewater and sludge.

The gas distribution when only R1 and R2 aerated was also calculated by MLGF. The simulation results are shown in Fig. 4. The GVF of fluid near aerators was high, and the wastewater close to impellers also contained more volume of gas which might be attributed to the phenomenon that the impellers pushed and stirred nearby fluid which made the mass exchange more frequent and easier in vertical direction. GVF decreased with the depth, most of regions, except areas near wastewater inlet, aerators and impellers, holding a GVF of only 10% or less, and this fraction decreased to a much smaller value on the lower layer. Thus, it could be inferred   that DO of lower layer was mainly transferred with the flows from the upper layer. Along the direction of mainstream, GVF of middle and upper layers of inner ditches was high, due to the cooperation of aerators and impellers.

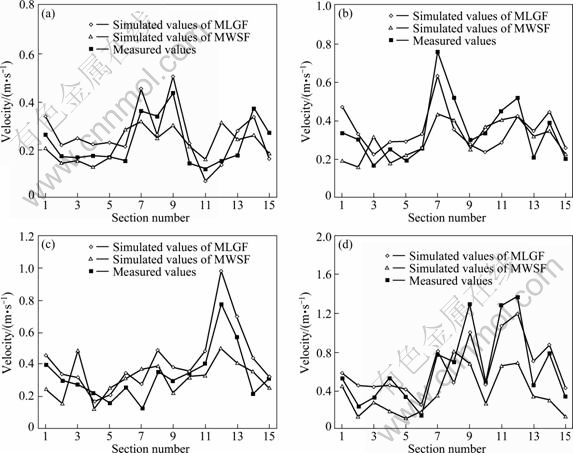
Fig. 3 Comparison of simulated velocities by two models and measured values at middle line of oxidation ditch: (a) Lower layer, z=0.5 m; (b) Middle layer, z=1.5 m; (c) Upper layer, z=3.0 m; (d) Surface, z=3.5 m

Table 2 Comparison of velocity simulated errors by two models at middle line of oxidation ditch

Fig. 4 Simulated gas distributions by MLGF: (a) Lower layer, z=0.5 m; (b) Middle layer, z=1.5 m; (c) Upper layer, z=3.0 m

The distribution of DO concentration in the oxidation ditch was also obtained during field measurement at Fendu WWTP. The monitor sections of DO were placed same with wastewater velocity. The measured DO distribution was compared with simulated GVF distribution in Fig. 5. It was shown that DO and GVF had a similar distribution. On the same monitor section, upper layer contained highest DO and GVF, followed by middle layer and then lower layer, and for each layer, the area from S8-S12, especially for the upper layer, had comparatively larger values of DO and GVF. One difference between the two kinds of distribution was that the GVF distribution lines were flatter with slighter fluctuations, indicating DO distribution was still affected by flow velocity, pollutant distributions, temperature field and other factors.

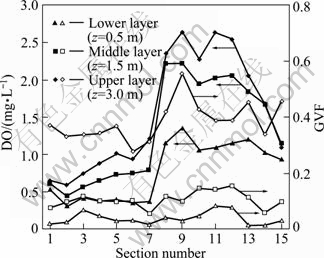
Fig. 5 Comparison of measured DO concentration and simulated GVF

3.2 Discussion

The velocity simulation results were not very satisfiable for the somewhat large errors which were generally higher than 20%. The reason was explained from two chief aspects, model simplification and field measurement. On one hand, aerators and impellers in model were simplified from their original shapes. Although the simulated results of flow field around the aerators and impellers were improved through parameter calibration, there were still some inevitable errors. For example, the simplified aerators cannot model the water spray and plunge which are the common phenomena in reality. On the other hand, plenty of eddies and other complicated flow structures existed in the oxidation ditch, not only challenging the accuracy of simulation, but also introducing difficulties for field velocity measurement. Besides, the rotating cup of velocimeter was intensively interfered, which also led to measurement errors.

The modeling method for liquid-gas flow, together with the calibration method proposed in this work, could be taken as an instruction to build hydrodynamic models of liquid-gas two-phase flow for oxidation ditches with surface aerations. GVF yielded from the MLGF is a crucial basis for simulation of DO, for it decides the DO flux and should significantly affect the distributions of DO and other components, e.g. chemical oxygen demand. In the hydrodynamics-bioreaction model proposed by ZHANG et al [14], which coupled MWSF with activated sludge model 2 (ASM2) through the advection- dispersion equations, the DO distribution adopted was obtained by field measurement, not by simulation methods, which limited the model application in practice. Nevertheless, velocity field and distribution of sludge and wastewater, in which the soluble components exit and most bioreactions happen, are also required for the simulation of DO and other component distributions in terms of a hydrodynamics-bioreaction model. MSWF separates sludge from wastewater and gives a result of velocity field of wastewater and sludge distribution, which are the advantages compared to MLGF, but it can not yield satisfiable results for upper layer and surface velocity, which makes its modelled values of upper layer and surface doubtful, while MLGF simulates GVF but cannot reflect the sludge distribution. It would be interesting to build a hydrodynamic model which combines the advantages of the two models. However, it is also found that the introduction of the third phase into the mixture model tends to computational divergence.

4 Conclusions

1) A MLGF is developed with aim at the simulation of liquid-gas two-phase flow in a full-scale Caroussel oxygen ditch with surface aeration. It is calibrated with the field measurement data and is used to model the wastewater velocity field and gas distribution of a full-scale Caroussel oxidation ditch with surface aeration.

2) The simulated velocities of MLGF are compared to that of MWSF. The velocity distribution from the two models shows similarities along the mainstream direction, and their simulated errors of velocities in the lower layer and middle layer are also comparable, but MLGF shows a better result for upper layer and surface, because MLGF considers the free movement of the interface between the two layers.

3) GVF distribution field simulated by MLGF is similar to the measured DO distribution, and shows flatter lines changing along the mainstream with fewer fluctuations, which indicates that the DO distribution is also affected by flow velocity, temperature, pollutant distribution and other factors. It has built an important basis to simulate DO and pollutant distributions in an oxidation ditch with surface aeration.

Nomenclature

References

[1] COCKX A, DO-QUANG Z, AUDIC J M, LIN? A, ROUSTAN M. Global and local mass transfer coefficients in waste water treatment process by computational fluid dynamics [J]. Chemical Engineering and Processing, 2001, 40(2): 187-194.

[2] FLUENT INCORPORATED. FLUENT 6.1 User’s guide [M]. Fluent Incorporated, 2003: 231-237.

[3] FAYOLLE Y, COCKX A, GILLOT S, ROUSTAN M, H?DUIT A. Oxygen transfer prediction in aeration tanks using CFD [J]. Chemical Engineering Science, 2007, 62(24): 7163-7171.

[4] MOULLEC Y L, POTIER O, GENTRIC C, LECLERC J P. Flow field and residence time distribution simulation of a cross-flow gas-liquid wastewater treatment reactor using CFD [J]. Chemical Engineering Science, 2008, 63(9): 2436-2449.

[5] OLMOS E, GENTRIC C, VIIAL C, MIDOUX N. Numerical simulation of multiphase flow in bubble column reactors: Influence of bubble coalescence and break-up [J]. Chemical Engineering Science, 2001, 56(21/22): 6359-6365.

[6] SPICKA P, DIAS M M, LOPES J C B. Gas–liquid flow in a 2D column: Comparison between experimental data and CFD modeling [J]. Chemical Engineering Science, 2001, 56(21/22): 6367-6383.

[7] VERMANDE S, SIMPSONA K, ESSEMIANIA K, FONADE C, MEINHOLD J. Impact of agitation and aeration on hydraulics and oxygen transfer in an aeration ditch: Local and global measurements [J]. Chemical Engineering Science, 2007, 62(9): 2545-2555.

[8] KRISHNA R, URSEANU M I, van BATEN J M, and ELLENBERGER J. Rise velocity of a swarm of large gas bubbles in liquids [J]. Chemical Engineering Science, 1999, 54(2): 171-183.

[9] PARKINSON L, SEDEV R, FORNASIERO D, RALSTON J. The terminal rise velocity of 10–100μm diameter bubbles in water [J]. Journal of Colloid and Interface Science, 2008, 322(1): 168-172.

[10] SIMONNET M, GENTRIC C, OLMOS E, MIDOUX N. Experimental determination of the drag coefficient in a swarm of bubbles [J]. Chemical Engineering Science, 2007, 62(3): 858-866.

[11] TALAIA M A R. Terminal Velocity of a Bubble Rise in a Liquid Column [C]// World Academy of Science, Engineering and Technology, 2007, 28: 264-268.

[12] GUO Li-sha. Wastewater-Sludge two-phase model and liquid-gas two-phase model of carrousel oxidation ditch [D]. Chongqing College of Resources and Environment Science: Chongqing University, 2010. (in Chinese)

[13] GUO Li-sha, ZHANG Dai-jun, XU Dan-yu, CHEN Yuan. An experimental study of low-concentration sludge settling velocity under turbulence condition [J]. Water Research, 2009, 43(9): 2383-2390.

[14] ZHANG Dai-jun, GUO Li-sha, XU Dan-yu, CHEN Yuan. Simulation of component distributions in a full-scale carrousel oxidation ditch: A model coupling sludge-wastewater two-phase turbulent hydrodynamics with bioreaction kinetics [J]. Environmental Engineering Science, 2010, 27(2): 159-168.

(Edited by HE Yun-bin)

Foundation item: Project supported by Visiting Scholar Foundation of Key Laboratory of the Resources Exploitation and Environmental Disaster Control Engineering in Southwest China (Chongqing University), Ministry of Education, China

Received date: 2011-07-26; Accepted date: 2011-11-14

Corresponding author: ZHANG Dai-jun, Professor, PhD; Tel: +86-23-65105875; E-mail: dzhang@cqu.edu.cn