Experiment and simulation of diffusion of micron-particle in porous ceramic vessel

LI Cai-ting(李彩亭)^{1, 2, *}, ZHANG Wei(张 巍)^{1, 2}, WEI Xian-xun(魏先勋)^{1, 2}, GAO Hong-liang(高宏亮)^{1, 2},

WEN Qing-bo(文青波)^{1, 2}, FAN Xiao-peng(樊小鹏)^{1, 2}, LIU Hai(刘 海)^{1, 2}, SHU Xin(舒 心)^{1, 2}, WEI Wei(魏 蔚)³

1. College of Environmental Science and Engineering, Hunan University, Changsha 410082, P.R.China;

2. Key Laboratory of Environmental Biology and Pollution Control of Ministry of Education,

Hunan University, Changsha 410082, China;

3. Guangzhou Hanhua Architects & Engineers Ltd., Guangzhou 510655, China

Received 113 Januaryuly 201009; accepted 46 JanuaryMay 2010

Abstract: The general behavior of micron-particles in the inner domain of porous ceramic vessel was simulated by computational fluid dynamics software in terms of sampling experimental data. The results show that there is an optimum porosity of 0.32 to get a higher efficiency and lower pressure drop during filtration. According to the results of simulation and experiment, it is evident that lower inlet velocity can maintain lower pressure drop and obtain higher collection efficiency and inlet concentration also has a crucial influence on the collection efficiency. The collection efficiency of equipment increases significantly with the increase of inlet concentration when the inlet concentration is less than 6.3 g/m³, but it gradually tends to be stable in the range of 97.3%-99.7% when the inlet concentration is over this concentration.

Key words: micron particle; ceramic vessel; pressure drop; porous medium

1 Introduction

Micron-particles of flue gas generated by industrial coal-fired boilers and kilns can do great damage to ecological environment and public health. Due to the complex behavior of micron-particles in different flow media, especially porous medium, many investigators[1-2] have pursued the turbulent and diffusion mechanisms and numerical simulations to explore non-steady thermal and mass-transfer problems of contaminant particles with microscopic motions. CHENG et al[3] discussed the measurement method of ultrafine particle concentration and size distribution in an iron foundry. SUN et al[4] observed fine particle aggregating behavior induced by high intensity condition. YANG et al[5] analyzed the damage of fine particles reinforced metal matrix composite by ultrasonic method.

Collecting fine dust particles by ceramic micro-pore filter is a crucial removal technique [U1] for industrial dust collection application. Nowadays, the porous medium filter is increasingly used [U2] in the dust collecting and desulfurization plants. COURY et al[6] researched capture and rebound of dust in granular bed gas filters by experimental data for the efficiency of filtration of gases in 1987. PODG?RSKI et al[7] reported theoretical and experimental studies on the deposition of stiff fibrous particles in granular bed filter. SMID et al[8] introduced an approach to remove the fine particles from high temperature and high pressure gas streams in 2004. HSIAU et al[9] presented the results of a study of the flow patterns in a quasi two-dimensional cross-flow moving granular bed with systems of louvers and sublouvers in 2008.

As an important dry-type dust-collecting device, its inner flow state directly affects many properties such as pressure drop, mass transfer in porous medium, convection and diffusion, and collection efficiency. Recently, some theoretical and numerical researches on the multiphase flow states in porous medium dust collecting device have been executed. SCHMIDT[10] investigated the influence of the interfacial drag on the pressure loss of combined liquid and vapor flow  through particulate porous media. KUKRETI and RAJAPAKSA[11] developed a numerical model for simulating two-phase flow through porous media. YUE and E[12] discussed numerical methods for linear and nonlinear transport equations with multiscale velocity fields.

On the basis of previous [U3] researches, this study mainly focuses on the procedure of mass transfer, convection and diffusion of nanoparticle aerosol through porous ceramic medium by using discrete particle model (DPM) and computational fluid dynamics (CFD) theory. Simultaneously, the corresponding characterization of carbon black and porous ceramic medium are presented. Finally, the experimental data are compared with the simulation results.

2 Theory and modeling

The incompressible Navier-Stokes (N-S) equations supplemented by computational fluid dynamics technology, some suitable turbulence models such as k—ε (Stand, RNG and Realizable) and Reynolds stress model (RSM) have provided theoretical basis for modeling the flow in porous ceramic vessel. The physical model consisting of inlet tube turbulence zone, dust hopper turbulence zone, porous laminar zone, clean gas turbulence zone and outlet tube turbulence zone is simulated by Euler-Lagrange discrete phase model because volume fraction of ultrafine particles is less than 10%. Moreover, the continuous phase in turbulence zone strictly satisfies N-S equation and discrete phase can use suitable discrete model.

2.1 Laminar flow

Since the velocity of mixture flow is very slow and the force is very small, the mixture flow (continuous phase and discrete phase) in porous laminar zone can be regarded as [U4] steady state Laminar flow. [U5]  Considering the effect of friction of ceramic pores, the N-S equation should be revised to present the process of the discrete phase flowing through porous ceramic medium. The discrete and continuous flow can be respectively calculated according to the movement equations of discrete phase and the momentum equation of phase continuous. The model can be simulated by using CFD method according to the fixed bed adsorption theory proposed by AUGIER et al[13] and the solving method of flow behavior and particle dispersivity of granular flow reported by JAFARI et al[14]:

                                    (1)

for continuity of continuous phase and

 (2)

for momentum.

where u_i is the fluid velocity in porous zone, is porosity, is fluid density, is flow distance in direction, u is velocity, t is time, is fluid dynamic viscosity and F is source item.

There are three assumptions [U6] in porous zone: a uniform velocity is assumed in the porous zone, no transition zone is generated at the gas-solid interfaces and no transversal slip occurs in pathlines direction.

2.2 Turbulent flow

Due to the mass conservation for all flows, the mass increment in a unit volume per unit time equals to the mass difference between the inlet and outlet of the unit volume. So, the continuity equation is

                            (3)

Eq.(3) is the general form of the mass conservation equation and is valid for incompressible flow. Due to no special phenomenon in turbulent flow such as phase transformation, the source is defined as zero.

Since all flow cases must satisfy momentum conservation law, that is, the Newton’s second law, so the momentum transfer equation of system is

              (4)

where i, j represent two different directions, p is pressure on a fluid micro element, F_i is the momentum source that includes two parts resulted by porous zone: the former is viscous resistance loss caused by Darcy’s percolation process and the latter is inertial resistance loss caused by the permeability of porous media. The formula of F_i is

                       (5)

where 1/α is viscous resistance coefficient and C₂ is inertial resistance coefficient.

To simply computation of coefficient 1/α and C₂, the porous ceramic media are regarded as homogenous.

The standard type of k—ε equation is based on the hypothesis of isotropic eddy-viscosity, which is modeled through the flow fields of the turbulent kinetic energy and the specific dissipation rate[15]. Considering the effect of turbulent swirl, [U7] low-Reynolds-number and near-wall region, the RNG k—ε model was derived using a rigorous statistical technique to enhance accuracy for swirling flows. In this work, RNG k—ε model is applied in all non-porous flow zones. The transport equations of RNG k—ε model are

               (6)

  (7)

                     (8)

where k is turbulent kinetic energy; ε is dissipation rate; μ_eff is effective viscosity; μ_t is turbulent viscosity; C_1ε and C_2ε are constants; α_k and α_ε are respectively the inverse effective Prandtl numbers for k and ε; η=S_k/ε; η₀=4.38, β=0.012; C_μ= 0.0845; S_k is user-defined source term.

In Eq.(7), the additional term R_ε makes model more responsive to the effects of rapid strain and streamline curvature than the standard k—ε model.

2.3 Discrete phase

The surface morphologies of carbon black particles were investigated by JSM-6700F field emission scanning electron microscope(FE-SEM). The typical crystallite of carbon black nanoparticles is shown in Fig.1. It is evident that the general carbon black particles appear as spherical crystallite micro-particles with the size of about 100 nm in standard state. The crystalline phases of supported samples in the fly-ash state were studied by X-ray diffractometry (XRD) (Fig.2). The chemical composition of compound phases was estimated according to the lattice parameter offset calculated by the angular position of the metal reflections using the Vegard’s law. Identification result of carbon black sample shows that the chemical composition is mainly composed of PbF₂, SiO₂, C₆₀, CaCO₃ and Al₂O₃. This result matches with microanalysis report of EDX test properly.

Fig.1 FE-SEM photograph for carbon black nanoparticles

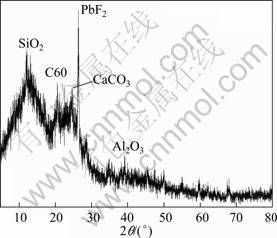
Fig.2 XRD of carbon black nanoparticles

In this work, we presumed that carbon black particles rebound back or deposit on the filter after colliding with the wall. The deposit processes satisfy particle erosion and accretion theory. According to statistical cumulative undersize distribution using 400 particle samples of 8 FE-SEM photographs, it shows that the carbon black nanoparticles obey Rosin-Rammer (R-R) distribution. The cumulative undersize distribution is

           (9)

where d_p is the measured carbon black equivalent diameter; n is the distribution exponent; `d<sub>p</sub> is carbon black equivalent mean diameter when G=0.632. The corresponding parameters in R-R distribution are obtained by experiment and interpolation: n=0.8263, `d_p =34.254 nm, the minimum equivalent diameter is 9.05 nm and the maximum equivalent diameter is 190.68 nm. The fitting curve of R-R distribution matches with experimental data properly, as shown in Fig.3.

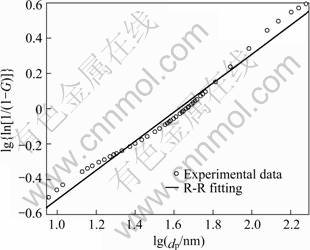
Fig.3 Rosin-Rammer fitting curve of carbon black nanoparticles

In the model, particles injection and air flow inlet lie on the same inlet surface. The discrete phase composed of carbon black nanoparticles has the specific motion equation. Due to the interaction between air and sub-micron particles in actual movements, the turbulent movement of air will improve or impede the motion of discrete phase in non-porous zones. Particle drag force from mixing and coupling process between continuous phase and discrete phase produces coupling movement velocity to interact each other. The motion equation of a spherical aerosol particle with consideration of the nonlinear drag force, Saffman Lift Force and the gravitational force is given as[16]

                    (10)

where u_p is the carbon black nanoparticles velocity; F_d is the drag force; F_L is the Saffman lift force; B_r is Brownian random and G is the gravity.

2.4 Physical characteristics of porous ceramic vessel

General speaking, there are several kinds of pore diameter series in adsorbent and the equivalent radius of every series has a certain range. According to the definition presented by DUBININ et al[17], the pore diameter can be divided into four ranges: the pore channel is defined as micropore (r_p<0.6-0.7 nm), sub-mesopore (0.6-0.7 nm < r_p < 1.5-1.6 nm), mesoproe (1.5-1.6 nm < r_p < 100-200 nm) and macropore (r_p > 100-200 nm).[U8]  The diffusion mechanism of particle pollutant is correlative with pore diameter, adsorbate concentration, pressure drive, temperature difference, etc. The diffusion [U9] in the porous media can be described by Fick’s Law[18].

The surface morphologies and chemical composition were tested by TEM-3010 high resolution transmission electronic microscope. The typical crystallite of ceramic material is shown in Fig.4. It is evident that the general ceramic particle appears to rough edge ellipsoidal crystallite particle with the size of about 1 μm in standard state. HUANG et al[19] developed an approach of quantitative measurement of porosity and pore size distribution, which is employed in the present study. By this way, we can take the logarithm of equivalent pore diameters and divide them into 20 levels.[U10]  With 80 fields in a single measure and 10 times of repeated measure, we could obtain the average value in the porous media with different porosities respectively. Identification result of ceramic material sample shows that the chemical composition is mainly composed    of Ca₂SiO₄, (KPO₃)₄?12H₂O, mullite, CoCl₂?6H₂O, W₂N (Fig.5).

Fig.4 TEM photograph for porous ceramic media absorbent

Fig.5 XRD patters of porous ceramic media

This model forms a closed domain by many porous ceramic media vessels and the basic work principle is similar to that of bag filter. Actually there are obvious differences from bag filter in the filtration mechanism. The work principle of bag filter is that the powder dusts are accumulated into prime layer on the bag surface by particles interception, inertia collision, electrostatic force and diffusion. Particularly the prime layer of bag filter becomes the main filtration layer[20]. Besides the efficacy of bag filter, many complex physical and chemical phenomena of ultrafine particle occur such as mass transfer, convection, diffusion and adsorption in the inner porous zones of porous ceramic media tubes. In this work, the physical transfer of aerosol contamination is mainly considered in the coupling process of carbon black and porous media by ignoring the influence of chemical reaction, which includes diffusion and adsorption. Mass diffusion coefficients are used to compute the diffusion flux of a chemical species in a laminar flow using Fick’s Law[21]：

                            (11)

where J_i is the diffusion flux of contaminant; ρ_c is the density of contaminant; D is the dynamic dispersivity  coefficient; C_i is the concentration of contaminant.

The channel size of porous ceramic media filtration material has a significant influence on diffusion mode of aerosol nanoparticles. When nanoparticles penetrate into macropore, the diffusion type appears to bulk diffusion since the channel diameter is far larger than mean free path of particles. When nanoparticles penetrate into mesopore of sub-mesopore, the diffusion type appears to Knudsen diffusion since the channel diameter is less than mean free path of particles. When nanoparticles penetrate into micropore, some particles are attached on the interior wall surface due to van der Waals force and some particles clog the micropores because the particle size exactly conforms to the pore size. The transport equation can be expressed as

           (12)

where U is velocity vector; K is the permeability of porous media.

The process described by Eq.(12) is inter-particle diffusion and mass transfer, that is, some nanoparticles are adsorbed from gas phase to adsorbent solid phase. D [U11] is composed of the sum of sub-micron particles dispersivity [U12] coefficient and mechanical dispersivity [U13] coefficient.

D = D_d + D^*                                (13)

where D_d is sub-micron particles dispersivity coefficient, D^* is mechanical dispersivity coefficient.

Dispersivity [U14] coefficient of sub-micron particles depends on contamination permeation velocity [U15] u in porous media, Pelect number and geometric characteristics of porous media.

                                  (14)

where u is the permeation velocity; d is the mean diameter of ceramic granular; Pe is the Pelect number.

The test results of metallographic microscope show that porous ceramic media property is stable and the pore size distribution of porous media satisfies Gaussian distribution. Consequently, the hypothesis of isotropy of porous media is applied and mechanical dispersivity tensor coefficient can be formulated as follows:

                 (15)

where D_T and D_L are respectively transversal dispersivity and longitudinal dispersivity, δ is Kronecker δ-function. DELGADO[22] studied the experimental methods and correlation coefficient of transversal dispersivity and longitudinal dispersivity in detail.

Additionally, the mass transfer process satisfies linear drive force (LDF) equation[13, 23]:

                             (16)

where q is the mass of contaminant deposited on porous media; q_i^* is the deposit mass of contaminant at equilibrium; q_i is the instantaneous deposit mass.

2.5 User define functions (UDFs)

As an essential supplementary of variable LDF and variable concentration of discrete phase, user define functions (UDFs) are important custom-defined forms of variable scalar because there is no variable drag force source provided for the coupling process of discrete phase and porous media zone and the contamination transfer-dispersivity-adsorption equation is not contained in the standard form of Fluent software. In this work, some coupled mixtures of carbon black nanoparticles and continuous phase flow into the macropore firstly; and the remains flow into mesopore and sub-mesopore after parts of them are absorbed by macropore, and then a small amount of mixture flows into micropore after parts of them are intercepted by mesopore and sub-mesopore; finally, the trace gaseous contaminants permeate into intra-particle zone after parts of them are absorbed and intercepted by micropore. The contamination adsorbates present parabolic distribution in the inner zone of adsorbent.[U16] 

The above process can be simplified by Gluckauf’s linear driving force model (LDFM) in UDFs, that is, the computation process is simplified greatly when LDFM is used as partial differential equation drive force model for material balance to make contamination particles diffuse onto adsorbent surface from continuous phase driven by concentration difference drive force ?q.

Function Define_Dpm_Source is used to define the source item of discrete phase equation, the general expression of which is

                              (17)

whereis dependent variable; S_c is the explicit part of the source term; S_k is the implicit part of the source term.

3 Results and discussion

3.1 Resistance characteristic of porous media

Fig.6 presents the relationship of system pressure drop and inlet velocity under different porosities. It is evident that the finer porosity in the calculation domain has more significant effect on the variation of curves while the effect of larger porosity is very weak. In this simulation, it is found that the porous media with φ=0.35 have the weakest effect and the porous media with φ=0.30 have the most effect under the operating conditions. At the inlet velocity of 4 m/s, the pressure loss decreases by 250 Pa while the porosity varies from 0.30 to 0.35. At the inlet velocity of 8 m/s, the pressure loss decreases by 600 Pa while the porosity varies from 0.30 to 0.35. If keeping the porosity as a constant, the P—V  presents parabolic curve regularly. Since the flow state belongs to low velocity range (u≤10 m/s), however, the tendency curve approaches linear law approximately. Fig.7 shows the comparison of tendency curve of pressure drop and collection efficiency with porosity. The perfect condition for dust-collecting device is low resistance and efficient dust-collecting performance in practical application. In fact, the two cases are contradictory: if the efficient dust-collecting performance is obtained, then the pressure drop is large and vice versa. So, we must seek an optimum porosity of pressure drop and collection efficiency for system. According to the two curves in Fig.7, it is found that the collection efficiency (η) can attach 99.3% and pressure drop of system is lower than  1 000 Pa when the porosity is 0.32, which exactly meets the requirements of practical operation. The pressure loss increases by 720 Pa with the porous media at the porosity of 0.32 when the inlet velocity varies from 4 to 9 m/s, as reported in Fig.8. Compared the experimental data with RNG k—ε simulation curve, the clustering tendency of data point near the simulation curve is observed distinctly, which shows that the RNG k—ε simulation results accord with the actual work.

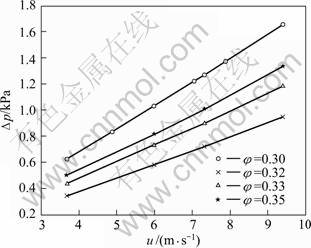
Fig.6 Relationship between pressure drop Δp and inlet velocity u corresponding to different porosities

Fig.7 Relationship of p and η with φ at inlet velocity of 7.325 m/s and inlet concentration of 4.5 g/m³

System pressure loss mostly comes from viscosity resistance and inertial resistance of porous media, friction pressure loss and local pressure loss of pipe. Resistance coefficients of various porous media are listed in Table 1 in terms of experimental ceramic vessels and derivation of Ergun’s equation. It is verified by simulation and experiment that pipe pressure loss is far less than resistance of porous media, that is, pipe pressure loss can be ignored comparatively. Thereby, system pressure loss is favorably induced as the theoretical parabolic curve formulation of porous media.

?p = au² + bu                               (18)

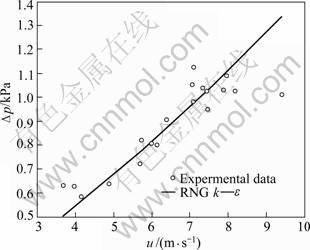
Fig.8 Comparison of experimental data and simulation curve of Δp—u with porosity of 0.32

Table 1 Resistance coefficients of various porous media

3.2 Frequency distribution of escaping dust particles

The experiments are performed for the porous media with porosity of 0.32 and mean pore diameter of 5.12μm and the dust samples have maximum equivalent of 190.68 nm and mean equivalent of 34.254 nm. Since the pore diameter of porous media is far larger than the free path of particles, the dust particles act as bulk diffusion inside the capillary tubes of porous media[24]. The main movements are inter-particles collisions and the accidents of particles-to-wall collisions belong to little probability. As a consequence, the corresponding modification for diffusion coefficient only need consider porosity φ and tortuosity factor τ. Then the modified diffusion coefficient is

                                 (19)

The removing principle of dust contamination using porous ceramic mainly depends on the collision and adhesion [U17] with complex tortuosity capillary channels and tubes. Since the particle size of 9.05-197.32 nm is far less than the pore size, the probabilities of capturing the carbonblack particles with any size are nearly equal. So, the frequency distribution of escaping particles basically remains 8-12% (Fig.9).

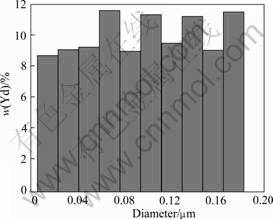
Fig.9 Frequency distribution histogram of escaping particles on outlet surface

3.3　Collection efficiency

Fig.10 illustrates the comparison of the collection efficiencies of simulations and experiments at three experimental velocities: 6.24 m/s, 7.33 m/s and 7.84 m/s. The result shows that the collection efficiency of simulation is coincident with the experimental data and it enhances with increasing the inlet concentration of aerosol contaminant. As shown in Fig.10, the experimental collection efficiency can reach 96.7%-98.02% and the theoretical collection efficiency computed by CFD can reach 97.3%-99.7% at C_in ≥ 6.3 g/m³ and it enhances obviously with decreasing the flow velocity.

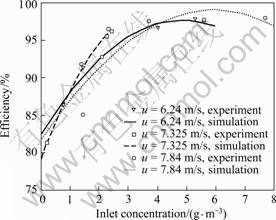
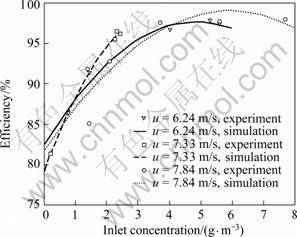
Fig.10 Collection efficiency comparison of simulations and experiments in three schemes

4 Conclusions

1) A numerical model of porous ceramic medium filter is implemented by experiment and CFD simulation in this study. It is found that the current porosity during the filtration of carbon black nanoparticles has enormous influence on the pressure drop and collection efficiency. The result shows that if the porosity is too small, the collection efficiency is high but the pressure loss will severely rises, and vice versa. This study indicates that the porosity of φ=0.32 is the optimum intersection point of pressure drop and collection efficiency.

2) The study proves that the method of separation and filtration of carbon black nanoparticles from flue flow is feasible by porous ceramic media with the porosity of micron size. From the analysis of escaping particles distribution and collection efficiency, the sensitivity of carbon black nanoparticles to pore diameter size is weak and to porosity φ or tortuosity factor τ is high.

3) The medium and low inlet gas velocity can get higher collection efficiency. In the low concentration range, collection efficiency increases quickly with the concentration rising. The efficiency curves gradually tend to be steady [U18] in the high concentration range.

References

[1] HUI Jing, XU Ting-xiang, ZHANG Li-te, GAO Tie-yu. Numerical calculation of gas flows in high temperature ceramic filters [J]. Journal of Xi’An Jiaotong University, 2009, 39(5): 463-467. (in Chinese)

[2] LI Hai-xia, JI Zhong-li, WU Xiao-lin, HE Qing-peng. Calculation of transient flow field in filter vessel containing three ceramic filters [J]. Chemical Industry and Engineering Progres, 2005, 24(8): 905-924. (in Chinese)

[3] CHENG Y H, CHAO Y C, WU C H, TSAI C J, UANG S N, SHIH T S. Measurements of ultrafine particle concentrations and size distribution in an iron foundry [J]. Journal of Hazardous Materials, 2008, 158: 124-130.

[4] SUN Wei, HU Yue-hua, DAI Jing-ping, LIU Run-qing. Observation of fine particle aggregating behavior induced by high intensity conditioning using high speed CCD [J]. Trans Nonferrous Met Soc China, 2006, 16(1): 198-202.

[5] YANG Zhi-guo, LONG Shi-guo. Damage analysis for particle reinforced metal matrix composite by ultrasonic method [J]. Trans Nonferrous Met Soc China, 2006, 16: s652-s655.

[6] COURY J R, THAMBIMUTHU K V, CLIFT R. Capture and rebound of dust in granular bed gas filters [J]. Powder Technology, 1987, 50(3): 253-265.

[7] PODG?RSKI A, ZHOU Y, BIBO H, MARIJNISSEN J. Theoretical and experimental study of fibrous aerosol particles deposition in a granular bed [J]. Journal of Aerosol Science, 1996, 27(1): 479-480.

[8] SMID J, PENG C Y, LEE H T, HSIAU S S. Hot gas granular moving bed filters for advanced power systems [J]. Filtration & Separation, 2004, 41(10): 32-35.

[9] HSIAU S S, SMID J, TSAI S A, TZENG C C, YU Y J. Flow of filter granules in moving granular beds with louvers and sublouvers [J]. Chemical Engineering and Processing, 2008, 47: 2084-2097.

[10] SCHMIDT W. Interfacial drag of two-phase flow in porous media [J]. International Journal of Multiphase Flow, 2007, 33: 638-657

[11] KUKRETI A R, RAJAPAKSA Y. A numerical model for simulating two-phase flow through porous media [J]. Applied Mathematical Modelling, 1989, 13(5): 268-281.

[12] YUE Xing-ye, E Wei-nan. Numerical methods for multiscale transport equations and application to two-phase porous media flow [J]. Journal of Computational Physics, 2005, 210: 656-675.

[13] AUGIER F, LAROCHE C, BREHON E. Application of computational fluid dynamics to fixed bed adsorption calculations: Effect of hydrodynamics at laboratory and industrial scale [J]. Separation and Purification Technology, 2008, 63(2): 466-474.

[14] JAFARI A, ZAMANKHAN P, MOUSAVI S M, PIETARINEN K. Modeling and CFD simulation of flow behavior and dispersivity through randomly packed bed reactors [J]. Chemical Engineering Journal, 2008, 144(3): 476-482.

[15] LI Shan-hong, LI Cai-ting, ZENG Guang-ming, LI Si-min, WANG Fei, WANG Da-yong, LU Pei. Simulation and experimental validation studies on a new type umbrella plate scrubber [J]. Separation and Purification Technology, 2008, 62(2): 323-329.

[16] ZERAI B, SAYLOR B Z, KADAMBI J R, OLIVER M J, MAZAHERI A R, AHMADI G, BROMHAL G S, SMITH D H. Flow characterization through a network cell using particle image velocimetry [J]. Transport in Porous Media, 2005, 60(2):135-250.

[17] DUBININ M M, NEIMARK A V, SERPINSKY V V. Impact of the adsorbate compressibility on the calculation of the micropore volume [J]. Carbon, 1993, 31(7): 1015-1018.

[18] LEHNER F K. On the validity of Fick’s law for transient diffusion through a porous medium [J]. Chemical Engineering Science, 1979, 34(6): 821-825.

[19] HUANG Z F, CHU S L, LIAO J Q, PU J Q, ZHEN L Z. Quantitative measurement of ceramic uranium dioxide porosity and pore distribution [J]. Journal of Central South University: Science and Technology, 2007, 38(3): 409-412. (in Chinese)

[20] LI X, CHAMBERS A J, HELSTROOM R. Analysis of the motion of mechanically shaken filter bags [J]. Filtration & Separation, 1993, 30(2): 151-159.

[21] MILD K H.The kinetics of diffusion between a spherical cell and a surrounding medium with different diffusion properties [J]. Bulletin of Mathematical Biology, 1971, 33(1): 1-156.

[22] DELGADO J M P Q. A critical review of dispersion in packed beds [J]. Heat and Mass Transfer, 2006, 42 (4): 279-310.

[23] WU Y X, WANG X, CHING C B. Computational fluid dynamics simulation of the adsorption separation of three components in high performance liquid chromatography [J]. Chromatographia, 2002, 55(7/8): 439-445.

[24] JACKSON R. On the limit of bulk diffusion control and high permeability in porous catalyst pellets [J]. Chemical Engineering Science, 1974, 29(6):1413-1419.

(Edited by LI Xiang-qun)

Foundation item: Project(50878080) supported by the National Natural Science Foundation of China; Project(K0902006-31) supported by the Key Scientific and Technological Special of Changsha City in China

Corresponding author: LI Cai-ting; Tel: +86-731-88649216; Fax: +86-731-88822829; E-mail: ctli3@yahoo.com, alvin_zw@126.com

DOI: 10.1016/S1003-6326(10)60655-3