J. Cent. South Univ. Technol. (2010) 17: 1247-1250
DOI: 10.1007/s11771-010-0627-9
Optimal design of V-type ultrasonic motor
JEONG S S, PARK C H, PARK T G
School of Mechatronics, Changwon National University, Changwon 641-773, Korea
? Central South University Press and Springer-Verlag Berlin Heidelberg 2010
Abstract: V-type ultrasonic linear motor fabricated using a simple punching technique was proposed to utilize as an actuator of small precision machine. The stator of the motor is composed of a thin elastic body and four ceramics attached to the upper and bottom areas of the body. The ceramics have each direction of polarization. When two harmonic voltages with a 90° phase difference are applied to the ceramics, symmetric and anti-symmetric displacements will generate at the tip to produce an elliptical motion. A finite element analysis (ATILA) was conducted to simulate the motion pattern for the contact tip of the stator. To develop a model that generates the maximum displacement at contact tip, the FEM program was used for various lengths. In addition, an optimal model was chosen by considering the magnitude and shape of the displacement according to changes in frequency. The maximum elliptical displacement is shown by W2L11 model, which has a ratio of ceramic width to length of 1:5.5. However, the displacement of the contact tip is reduced by the bucking phenomenon if the ratio is larger than 1:6.
Key words: ultrasonic motor; piezo-actuator; finite element method; optimal design; elliptical motion
1 Introduction
Ultrasonic motors have been continuously developed since the first invention in 1973 and many researches on the motors have been studied in Japan and USA. The characteristics of ultrasonic motor have various features, such as high torque at low speed, large power output per unit weight, and the possibility of precise positioning. The features caused to be possible to conduct the researches on the use as a zoom lens of cameras and actuators of precise x-y stage. Recently, there has been a rapid increase in demand for small motors for electronic appliances with the development of the industrial technology. The minimum size of an electromagnetic motor is generally limited to about 1 cm [1-4]. Since there are limits to the miniaturization of electromagnetic motors, ultrasonic motor is a viable alternative for small spaces. The motor should have an easy manufacturing process to overcome the limits of miniaturization [5-10].
Existing ultrasonic motors have excellent response speed, accuracy, and high efficiency. However, in practice, it is very difficult to use them as small motors due to their complicated structure and expensive cost [11-15]. V-type ultrasonic motors can be easily fabricated using the simple punching technology because the motor structure consists of 0.1 mm-thick ceramics
attached to a 0.1 mm-thick elastic body. In this work, a V-type ultrasonic motor that can be fabricated as a small and simple structure was proposed. For optimal design of the proposed V-type model, changes in the characteristics due to changes in length were analyzed by using the FEM program. Similarly, the model generating maximum elliptical displacement was chosen by analyzing the resonance mode according to changes in frequency, maximum displacement of the resonance point, and elliptical displacement of the resonance mode.
2 Structure of motor
Fig.1 shows the polarization direction and applied voltage of the ceramics and the shape of the V-type ultrasonic motor. The stator structure was composed of four ceramics, each polarized in a direction, which were attached to the upper and bottom areas of the thin elastic body. When two sinusoidal waves with a phase difference of 90? were applied, as shown in Fig.2, elliptical displacement will be generated at the contact tip for one cycle (t0-t3). Fig.3 shows the motion of the contact tip for one cycle. The motion of the stator was represented in detail with FEM [7-9]. The rotation direction of the rotor was determined through the motion of the contact tip. The inverse motion could apply the inverse phase of the applied voltage to the stator.
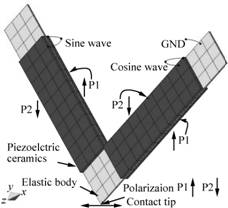
Fig.1 Structure of V-type ultrasonic motor
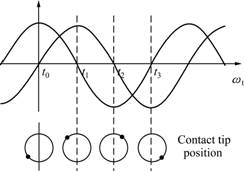
Fig.2 Schematic diagram of elliptical motions of contact tip

Fig.3 Schematic diagram of elliptical motion of contact tip for one cycle
3 FEM simulation
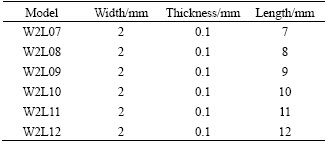
The finite element analysis program ATILA was used to simulate the characteristics of the stator. The motor is affected by the length of ceramics because the vibration mode is used as the longitudinal vibration mode of piezoelectric ceramics [1, 11]. The width and thickness of the ceramics were determined to be 2 and 0.1 mm, respectively. Six models were chosen by increasing the lengths of the ceramics in increments of 1 mm from 7 to 12 mm. The length of 7 mm wasdetermined to be the minimum length generating a vibration in the longitudinal vibration mode by the FEM program [4-8]. Table 1 shows names and sizes of the analyzed model.
Table 1 Names and sizes of analyzed model
Resonance modes were verified to be 20-200 kHz by using FEM. Resonance modes according to change in frequency are shown in Fig.4, where five resonance modes are represented. The resonance frequency decreases with the increase of ceramic length. In Fig.4, only the resonance characteristics of W2L07 model are represented because the six models all show the same modes.
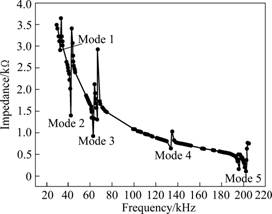
Fig.4 Impedance characteristics of W2L07 model (Resonance mode)
The vibration shapes of each mode were verified through modal analysis. Frequencies representing the vibration mode in the longitudinal vibration mode were analyzed by harmonic analysis. In the analysis results, elliptical displacements are generated in modes 2 and 3. The displacement magnitude of mode 1 is small. For modes 4 and 5, complex vibrations are generated. Therefore, the frequency ranges of modes 2 and 3 should be used for operation of the motor.
Fig.5 shows the displacement magnitudes of modes 2 and 3. The displacement of mode 3 is larger. In particular, the displacement of W2L11 model is larger than that of other models. The displacement shown in Fig.5 is not elliptical displacement that can be used for the ultrasonic motor but the displacement of resonance frequency. Elliptical displacements are generated at off-resonance out of the resonance frequency. Fig.6 shows the maximum elliptical displacement for each model. The off-resonance is slightly out of resonance frequency. The maximum elliptical displacement is found by verifying each frequency for the models, separately. In the results, W2L11 model has the largest elliptical displacement, which is proportional to the displacement magnitude of the resonance frequency. According to the vibration theory for the longitudinal vibration mode of ceramics, the displacement magnitude is proportional to length. However, the displacement at the contact tip will decrease due to the bucking phenomenon when the motor length is too long. When the ratio of the ceramic width to length becomes 1:5.5, the bucking phenomenon will increase.
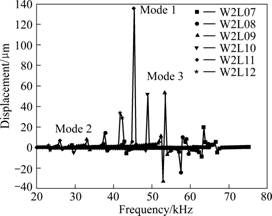
Fig.5 Displacement characteristics according to changes in frequency (Modes 2 and 3)

Fig.6 Comparison of maximum elliptical displacements in mode 3
W2L11 model representing maximum elliptical displacement was chosen as the optimal model; and the operation frequency fields of the ultrasonic motor were then determined by verifying displacements in the off-resonance fields. Fig.7 shows displacement changes of W2L11 near mode 3. After verifying the frequency fields, including above and below the resonance frequency, the maximum elliptical displacements are obtained to be close to the resonance frequency. Larger displacements are found at frequencies lower than the resonance frequency. When the frequency is not off-resonance, the magnitude of the displacement will decrease sharply. The speed and torque of the motor can increase depending on the increase in the elliptical displacement. According to the shapes of the elliptical displacement, the area contacting rotor changes. This should increase the torque of the ultrasonic motor due to the increase in both the contact area of the rotor and the magnitude of displacement. Fig.8 shows the off- resonance field near the resonance frequency. The frequency generating a minimum displacement of 1.5 μm is determined as the operation frequency field for the ultrasonic motor.
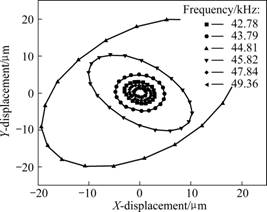
Fig.7 Displacement shapes of W2L11 model according to changes in frequency in mode 3
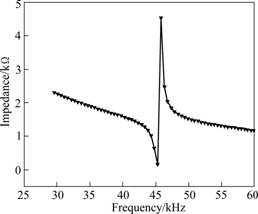
Fig. 8 Relationship between resonance and operation frequency fields of W2L11 model in mode 3
4 Conclusions
(1) A V-type ultrasonic linear motor is proposed. A finite element analysis (ATILA) is used to simulate the motion pattern of the contact tip of the stator.
(2) To determine a model that generates the maximum displacement at the contact tip, the FEM program is used to monitor changes in characteristics with changes in length. In addition, the optimal model is chosen by considering the magnitude and shape of displacement according to changes in frequency. When the ratio of the ceramic width to length is 1:5.5, the maximum elliptical displacement is shown by W2L11 model. However, the displacement of the contact tip will be reduced by the bucking phenomenon when the ratio is larger than 1:6. The maximum displacements are obtained at frequencies close to the resonance frequency. A frequency field of approximately 10 kHz generating up to 1.5 μm magnitude of displacement is determined to be the operation frequency field of the ultrasonic motor.
(3) Due to this definition of the operation frequency field, the motor can be controlled through frequency control. The proposed motor can be used as actuators for small precision instrument because of its simple structure and thin body.
References
[1] SASHIDA T. Trial construction and operation of an ultrasonic vibration driven motor [J]. Japanese Journal of Applied Physics, 1982, 21: 713-720.
[2] KO H P, KIM S S, BORODINAS S N, VASILJEV P E, KANG C Y, YOON S J. A novel tiny ultrasonic linear motor using the radial mode of a bimorph [J]. Sensor and Actuators A: Physical, 2006, 125(2): 477-481.
[3] PARK T G, KIM B J, KIM M H, UCHINO K. Characteristics of the first longitudinal-fourth bending mode linear ultrasonic motors[J]. Japanese Journal of Applied Physics, 2002, 41: 7139-7143.
[4] CHONG H H, PARK T G, KIM M H. A study on driving characteristics of the cross type ultrasonic rotary motor [J]. Journal of Electroceramics, 2006, 17(2): 561-564.
[5] SONG T H, RICHARD E, THOMAS R, CLIVE A, WES H. Piezoelectric properties in the perovskite BiScO3-PbTiO3- (Ba,Sr)TiO3 ternary system [J]. Japanese Journal of Applied Physics, 2003, 42: 5181-5184.
[6] KIM H W, DONG S, LAORATANAKUL P, UCHINO K, PARK T G. Novel method for driving the ultrasonic motor[J]. Institute of Electrical and Electronics Engineers, 2002, 49(10): 1356-1362.
[7] WANG X X, MURAKAMI K, SUGIYAMA O, KANEKO S. Piezoelectric properties, densification begavior and microstructural evolution of low temperature sintered PZT ceramics with sintering aids [J]. Journal of the European Ceramic Society, 2001, 21(10): 1367-1370.
[8] KO H P, KIM S S, KANG C Y, KIM H J, YOON S J. Optimization of a piezoelectric linear motor in terms of the contact parameters [J]. Materials Chemistry and Physics, 2005, 90(2): 322-326.
[9] HU H, FUDA Y, KATSUNO M, YOSHIDA T. A study on rectangular-bar-shaped multilayer transformer using length extensional vibration mode [J]. Japanese Journal of Applied Physics, 1999, 38(5): 3208-3212.
[10] MORITA T, KUROSAWA M K, HIGUCHI T, Cylindrical micro ultrasonic motor utilizing bulk lead zirconate titanate (PZT) [J]. Japanese Journal of Applied Physics, 1999, 38: 3347-3350.
[11] SAITO J, FRIEND J R, NAKAMURA K, UEHA S. Resonant mode design for noncontact ultrasonic motor with levitated rotor [J]. Japanese Journal of Applied Physics, 2005, 44: 4666-4668.
[12] KANDA T, MAKINO A, SUZUMORI K, MORITA T, KUROSAWA M K. A cylindrical micro ultrasonic motor using a micro-machined bulk piezoelectric transducer [J]. Sensor and Actuators A: Physical, 2006, 127: 131-138.
[13] HALL A, ALLAHVERDI M, AKDOGAN E K, SAFARI A. Development and electromechanical properties of multimaterial piezoelectric and electrostrictive PMN-PT monomorph actuators[J]. Journal of Electroceramics, 2005, 15(2): 143-150.
[14] KIM H W, PRIYA S, UCHINO K, NEWNHAM R E. Piezoelectric energy harvesting under high pre-stressed cyclic vibrations[J]. Journal of Electroceramics, 2005, 15(1): 27-34.
[15] RANDALLl C A, KELNBERGER A, YANG G Y, EITEL R E, SHROUT T R. High strain piezoelectric multilayer actuators—A material science and engineering challenge [J]. Journal of Electroceramics, 2005, 15(3): 177-191.
(Edited by CHEN Wei-ping)
Foundation item: Project supported by the Second Stage of Brain Korea 21 Project; Project(2009-0088570) supported by the National Research Foundation of Korea
Received date: 2010-06-29; Accepted date: 2010-09-22
Corresponding author: PARK T G, PhD, Professor; Tel: +82-55-2133631; E-mail: tgpark@changwon.ac.kr