文章编号：1004-0609(2009)10-1748-06

界面错配应力对铝合金粗化机制影响的微观相场模拟

马  锐，王永欣，陈  铮，苗海川，钟汉文，苗树芳

 (西北工业大学 凝固技术国家重点实验室，西安 710072)

摘  要：采用微观相场法研究铝基合金中界面错配应力对沉淀相粗化过程的影响。结果表明：界面错配应力为零时，粗化机制符合经典LSW机制；错配应力较大时，粗化机制是位向控制粗化机制，沉淀相颗粒沿弹性“软”方向规则分布；中等界面错配应力时，粗化机制为兼具位向控制和LSW机制的混合机制；界面错配应力促进沉淀相延弹性软方向生长；沉淀相的粗化过程和长大过程交叠进行。

关键词：铝合金；粗化机制；粗化速率；界面错配应力

中图分类号：TG146.2       文献标识码： A

Microscopic phase-field simulation of influence of interfacial mismatch stress on coarsening mechanism of aluminum alloy

MA Rui, WANG Yong-xin, CHEN Zheng, MIAO Hai-chuan, ZHONG Han-wen, MIAO Shu-fang

(State Key Laboratory of Solidification Processing, Northwestern Polytechnical University, Xi’an 710072, China)

Abstract: Influence of interface mismatch stress on precipitate coarsening process in aluminum alloys was investigated using a microscopic phase-field model. The results show that, when the interface mismatch stress is zero, the coarsening mechanism complies with the classic LSW theory. When the mismatch stress is large, the coarsening mechanism is orientation-controlled. The precipitate particles are distributed periodically along the elastic soft directions. At medium interface mismatch stress, the coarsening mechanism is mixed with both orientation-control and LSW mechanism. The interface mismatch stress promotes precipitate growing in elastic soft directions. The coarsening process and growth process of the precipitates overlap with each other in proceeding.

Key words: aluminum alloy; coarsening mechanism; coarsening rate; interfacial mismatch stress

合金沉淀过程中，由于沉淀相与母相之间晶格参数的差异而引起点阵错配，从而产生界面错配应力。界面能、界面错配应力及弹性各向异性因子决定了沉淀相的形貌和位向，使沉淀相在弹性应力作用下出现明显的位向性，尤其是对应共格、半共格界面时更容易引起沉淀相的定向生长和分布。沉淀相的位向性将导致合金性能各向异性，因而降低其韧性，提高缺口敏感性等。因此，研究界面错配应力影响下合金的沉淀过程是铝合金沉淀理论中的一个重要课题。

经典动力学理论将形核、长大和粗化作为独立的过程来处理，提出相应的动力学模型。经典的LSW粗化理论，对应于沉淀后期体积分数基本不发生变化的情况。实际上，依固溶体过饱和度不同，粗化可以伴随长大过程一起进行，甚至在形核阶段就开始。形核、长大和粗化过程必须看作是相互竞争和重叠的过程。LSW理论是基于球状孤立的沉淀颗粒建立的，该理论以及其在有限体积分数情况下的推广都假定粗化过程完全由相关界面能的释放来驱动^[1]，并未考虑界面错配应力的影响，因此，对存在点阵错配的粗化现象无法解释^[2]。本文作者采用的微观扩散方程可以应用于包括形核、长大和粗化在内的沉淀过程的所有阶段，自动将粗化作为伴随过程处理，同时考虑了界面错配应力的影响，使研究过程更加真实，因而与其它模型相比具有显著的优点。

有关界面错配应力对沉淀相颗粒形状及空间相关性的研究已有许多报道^[3-6]，但关于界面错配应力对铝合金粗化过程的研究报道较少。本文作者以二元铝基模型合金为例，探讨错配应力作用下沉淀相的粗化行为、错配应力的大小以应变能的参数表征，由不同大小的错配度计算得出。

1  理论模型

微观扩散方程实际为 Cahn-Hilliard 扩散方程的微观离散格点形式，它以原子占据晶格位置的几率为场变量来描述原子组态和相形貌。据 Onsager 扩散方程可知，几率的变化率与热力学驱动力成正比，即^[7]

式(1)为一确定方程，可直接用于描述相变中长大及粗化过程，添加一个热起伏噪声项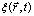后，使之也可用于模拟形核过程，即^[8]

式(2)为微观Langevin方程，一般经Fourier变换后，采用Euler方法在波矢空间中  求解。

离散格点形式的微观Langevin方程，无需预先设定沉淀相的结构，只需输入原子间相互作用势，计算机自动模拟可获得包括瞬时相在内的有序结构^[9]。同时考虑了沉淀相的粗化过程^[10-11]，克服传统粗化模型将第二相假设为由纯溶质原子构成，且两相界面明锐，以及第二相体积分数无限小等缺点，充分体现了形核、长大和粗化过程在时间上相互重叠、伴随等特点。

考虑界面错配应力，将式(1) Fourier变换后，得到其在倒易空间下的表达式为

在模拟过程中，对应变能，温度分别按式(6)进行约化，即

2  结果与讨论

在本模拟过程中取128×128个格点，溶质浓度x₀=14%，约化温度T^*=0.1，在每个方向上应用周期性边界条件。溶质原子在某一格点上出现的几率由灰度表示：完全黑色区域代表占位几率为0，完全白色代表占位几率为1，中间值用不同灰度表示。对微分方程(3)求解时取时间步长?t^*=0.001，约化的时间 t^*=n?t^*，其中n为迭代步数。

图1所示为界面错配应力为零时合金沉淀后期的组织演化图。从图1可以看出：沉淀相为球形，随机独立分布；在t^*=130时，颗粒大小不一，随着时间的延续，小颗粒消失，大颗粒长大，沉淀相颗粒数逐渐减少，尺寸不断增大；t^*=460时，颗粒的形状和颗粒间的相互分布特征仍然保持不变。这是因为忽略错配应力时，在相变驱动力中，界面能起主要作用，而球状颗粒的界面能最低。在沉淀相的演化过程中，可以清楚地观察到小颗粒溶解及大颗粒长大的现象，说明在不考虑错配应力的情况下，沉淀相的粗化机制为单纯的LSW机制。

图1  B^*=0时沉淀相粗化的组织演化图

Fig.1  Microstructure evolution of precipitates coarsening at B^*=0: (a) t^*=130, (b) t^*=260, (c) t^*=360, (d) t^*=460

图2所示为B^*=0时沉淀相颗粒半径的立方随时间的变化曲线。从图2中可以看出，粗化过程中，沉淀相平均半径的立方随时间的延长一直增大，且变化基本满足直线关系，说明不考虑界面错配应力时，沉淀相的粗化符合Ostwald熟化理论。

图2  B^*=0 时沉淀相颗粒半径的立方随时间的变化曲线

Fig.2  Changing curves of cube of average radius of precipitated particle with reduced time at B^*=0

图3所示为错配应力作用下B^*=0.849时合金沉淀后期的组织演化图。从图3可以看出，在考虑界面错配应力的条件下，沉淀相颗粒为椭片状，具有一定的方向性；在t^*=130时，沉淀相颗粒大小不一，随机分布；随着时间的持续，在t^*=460时，粗化基本完成，此时沉淀相颗粒沿着特定的方向排列，该特定方向称为弹性“软”方向，即[100]和[001]方向。铝基合金弹性各向异性因子为负值^[12]，界面错配应力在<100>方向上达到最小值，所以粗化完成后，沉淀相颗粒沿[100]和[001]方向规则排列。同时由图3可以发现，考虑错配应力时，合金的粗化过程并不是错配应力为零时单纯的大颗粒长大及小颗粒溶解的过程。在t^*=130时，图3(a)中标示的3个颗粒中最下面的颗粒最大，上排两个颗粒大小基本相当；在t^*=260(见图3(b))时，上排原来大小基本相等的两个颗粒中，左边的颗粒已经消失，右边的颗粒逐渐长大，尺寸已经大于正下方起初最大的颗粒；随着时间的延续，上面的颗粒继续长大，下面的颗粒逐渐减小，t^*=460(见图3(d))时完全消失，最终只有上面的颗粒单独存在。由图3(a)中3个颗粒的位置可以发现，上排右方的颗粒是处于弹性“软”方向上的，而其他两个颗粒则处于弹性“软”方向以外，所以在这组颗粒的粗化过程中，弹性“软”方向这一位置因素起了主要作用。这种现象与 Ostwald 熟化规律正好相反，称这种现象为应变诱发反向粗化^[13]。20世纪60年代，Khachaturyan 和Statalov基于能量最小原理预测过在一定条件下会出现这种反向粗化现象^[14]。JOHNSON等^[15]采用动力学方程在仅考虑两个粒子的条件下模拟得到过这种结论。由此可以看出，由合金沉淀过程产生的晶格错配引起的界面错配应力，对沉淀组织的形貌及颗粒的粗化行为有着显著的影响。错配应力作用下的粗化行为较为复杂，主要是因为弹性各向异性导致沉淀相并非球状，以及长程弹性交互作用使沉淀相产生强烈的空间关联，从而沿一定的晶体学方向排列。

图3  B^*=0.849及沉淀相粗化的组织演化图

Fig.3  Microstructure evolution of precipitates coarsening at B^*=0.849: (a) t^*=130; (b) t^*=260; (c) t^*=360; (d) t^*=460

由图3还可以发现，沉淀相颗粒的粗化具有择优取向：位于弹性“软”方向上的颗粒继续长大和粗化，位于弹性“软”方向外的颗粒逐渐消失，可以认为这是应变能弛豫的结果；而对位于同一行或列的颗粒而言，在界面能弛豫的驱动下小颗粒消失，大颗粒长大。综合以上情况可以认为，在应变能参数B^*=0.849时，沉淀相的粗化机制是由颗粒位向和LSW机制共同决定的混合机制。

图4所示为错配应力作用下，应变能参数B^*=1.687时合金沉淀后期的组织演化图。由图4可以看出，沉淀相椭片状的形貌比错配应力较小时更加明显。从图4(a)中可以看出，某些位置上相距较近的颗粒已经合并，尽管此时沉淀相颗粒仍然较小，但沉淀相长大和粗化在弹性“软”方向上的优先发展已经体现出来。在非弹性“软”方向上虽有部分沉淀相颗粒存在，但其尺寸相对于“软”方向上的颗粒来说比较小。由图4(a)和(b)可以看出，沉淀相颗粒在有利于生长的“软”方向上的粗化过程为非“软”方向上的颗粒消失，部分较近“软”方向上的颗粒合并，最终形成如图4(d)所示的沿[100]和[001]方向上的规则排列。综上所述，在应变能参数为1.687时，沉淀相的粗化过程为非“软”方向上的颗粒消失，部分较近“软”方向上的颗粒合并，其粗化机制主要以位向决定为主。

图4  B^*=1.687时沉淀相粗化的组织演化图

Fig.4  Microstructure evolution of precipitates coarsening B^*=1.687: (a) t^*=130; (b) t^*=260; (c) t^*=360; (d) t^*=460

图5所示为不同界面错配应力作用下沉淀相颗粒数目随时间的变化曲线。图中曲线上升阶段对应于沉淀相的形核过程，可以看出错配应力作用下，形核过程也受到一定的影响，随着错配应力的增大，形核过程有所加速，形核率有所提高，形核完成后颗粒数目增多。曲线下降阶段对应于沉淀相的粗化过程。粗化过程中，当错配应力为零时，曲线的下降速度最慢，粗化速率最小，这是由其单一的LSW粗化机制所决定的；随着错配应力的增大，曲线的下降速度加快，相同的时间步数下体系中所对应的颗粒数目减少，粗化速率加快，这是因为错配应力的存在使得沉淀相的粗化机制发生了改变，位向和LSW共同决定的混合机制更有利于粗化过程的进行，对粗化过程起到促进作用。错配应力越大，粗化速率越快。

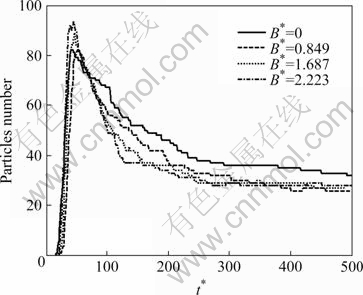
图5  不同界面错配应力作用下沉淀相颗粒数目随时间的变化曲线

Fig.5  Changing curves of particle number for precipitates of alloy at x₀=14% and different interfacial misfit stresses

图6所示为不同界面错配应力作用下，沉淀相体积分数随时间的变化曲线。由图6可看出，体积分数达到最大值后，4组曲线基本重叠在一起，在随后的过程中变化不大，说明体积分数受错配应力的影响较小。对比图5可以发现，当沉淀相体积分数不再变化时，颗粒数目却在急剧下降，这是因为沉淀相的粗化过程和长大过程交叠所致。

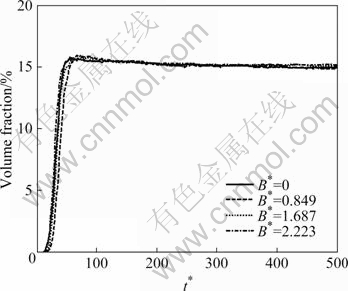
图6  不同界面错配应力作用下沉淀相体积分数随时间的变化曲线

Fig.6  Changing curves of volume fraction of precipitates with reduced time for alloys at different interfacial mismatch stresses

3  结论

1) 界面错配应力作用下，形核过程受到影响：随着错配应力增大，形核率有一定的提高，形核完成后，颗粒数目增多。

2) 界面错配应力为零时，沉淀相为随机独立分布的球状，其粗化机制为单一的LSW机制即颗粒溶解、大颗粒长大。

3) 考虑界面错配应力时，沉淀相为椭片状。错配应力作用下，粗化机制为位向和LSW共同决定的混合机制；随着错配应力的继续增大，粗化机制以位向决定为主；粗化完成后，颗粒沿[001]和[100]“软”方向规则排列。

4)界面错配应力作用时，两种机制共同作用的混合机制促进了粗化过程的进行，使粗化速率加快，错配应力越大，粗化速率越快；粗化过程和长大过程交叠进行。

REFERENCES

[1] CAHN R W, HAASEN P. 材料的相变[M]. 刘俊明, 译. 北京: 科学出版社, l998.
CAHN R W, HAASEN P. Phase transformation in materials[M]. LIU Jun-ming, transl. Beijing: Science Press, 1998.

[2] QIU Y Y. The effect of the lattice strains on the directional coarsening of γ′ precipitates in Ni-based alloy[J]. Journal of Alloys and Compounds, 1996, 232(1): 254-263.

[3] WEN Y H, CHEN L Q, HAZZLEDINE P M, WANG Y. A three-dimensional phase-field model for computer simulation of lamellar structure formation in γ TiAl intermetallic alloys[J]. Acta Materialia, 2001, 49: 2341-2353.

[4] 赵宇宏, 陈 铮, 刘 兵. 共格畸变影响沉淀相形貌的计算机研究[J]. 稀有金属, 2003, 27(1): 119-123.
ZHAO Yu-hong, CHEN Zheng, LIU Bing. Computer simulation of strain-induced morphological transformation of coherent precipitates[J]. Chinese Journal of Rare Metals, 2003, 27(1): 119-123.

[5] VAITHYANATHAN V, CHEN L Q. Coarsening of ordered intermetallic precipitates with coherency stress[J]. Acta Materialia, 2002, 50: 4061-4073.

[6] 卢艳丽, 陈 铮, 李永胜, 等. 包含共格畸变的立方合金沉淀机制的计算机模拟[J]. 稀有金属材料与工程, 2005, 34(8): 1205-1208.
LU Yan-li, CHEN Zheng, LI Yong-sheng, WANG Yong-xing, CHU Zhong. Computer simulation for the precipitation mechanism of the cubic alloy including coherent strain energy[J]. Rare Metal Materials and Engineering, 2005, 34(8): 1205-1208.

[7] KUPPER T, MASBAUN N. Simulation of particle growth and ostwald ripening via the cahn-hilliard equation[J]. Acta Materialia, 1993, 42: 1847-1858.

[8] PODURI R, CHEN L Q. Computer simulation of the kinetics of order-disorder and phase separation during precipitation of δ′(Al₃Li) in Al-Li alloys[J]. Acta Materialia, 1997, 45(1): 245-255.

[9] WANG Y, CHEN L Q, KHACHTURYAN A G. Kinetics of strain-induced morphological transformation in cubic alloys with a miscibility gap[J]. Acta Materialia, 1993, 14(1): 279-296.

[10] OKUDA H, OSAMURA K. Computer simulation of the kinetics of phase decomposition with the L1₂ type ordering in an Ising lattice system at low temperature[J]. Acta Materialia, 1994, 42: 1337-1343.

[11] PODURI R, CHEN L Q. Non-classical nucleation theory of ordered intermetallic precipitates application to the Al-Li alloy[J]. Acta Materialia, 1995, 44: 4253-4259.

[12] 魏齐龙, 陈 铮, 王永欣. T₁相(Al₂CuLi)对铝锂合金各向异性的贡献[J]. 有色金属, 2002, 54(3): 4-8.
WEI Qi-long, CHEN Zheng, WANG Yong-xin. Contribution of T₁ precipitate (Al₂Cu Li) to anisotropy in Al₂Li alloys[J]. Nonferrous Metals, 2002, 54(3): 4-8.

[13] 陈大钦, 郑子樵, 李世晨. 共格沉淀析出过程的模拟(Ⅰ)-微观结构演化[J]. 中国有色金属学报, 2005, 15(12): 1945-1952.
CHEN Da-qin, ZHEN Zi-qiao, LI Shi-chen. Simulation of precipitation process of coherent particles (Ⅰ)—microstructure evolution[J]. The Chinese Journal of Nonferrous Metals, 2005, 15(12): 1945-1952.

[14] LEE B C, PARK J K. Effect of the addition of Ag on the strengthening of Al₃Li phase in Al₂Li single crystals[J]. Acta Materialia, 1998, 46: 4181-4187.

[15] JOHNSON W C, ABINANDANAN T A, VOORHEES P W. The coarsening kinetics of two misfitting particles in an anisotropic crystal[J]. Acta Metall Mater, 1990, 38: 1349-1367.

(编辑 龙怀中)