J. Cent. South Univ. (2016) 23: 1486-1507

DOI: 10.1007/s11771-016-3201-2

Equivalent elastic compliance tensor for rock mass with multiple persistent joint sets: Exact derivation via modified crack tensor

CUI Jie(崔洁), JIANG Quan(江权), FENG Xia-ting(冯夏庭),

LI Shao-jun(李邵军), GAO Hong(高红), LI Shuai-jun(李帅军)

State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics,

Chinese Academy of Sciences, Wuhan 430071, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: Discontinuities constitute an integral part of rock mass and inherently affect its anisotropic deformation behavior. This work focuses on the equivalent elastic deformation of rock mass with multiple persistent joint sets. A new method based on the space geometric and mechanical properties of the modified crack tensor is proposed, providing an analytical solution for the equivalent elastic compliance tensor of rock mass. A series of experiments validate the capability of the compliance tensor to accurately represent the deformation of rock mass with multiple persistent joint sets, based on conditions set by the basic hypothesis. The spatially varying rules of the equivalent elastic parameters of rock mass with a single joint set are analyzed to reveal the universal law of the stratified rock mass.

Key words: equivalent elastic compliance tensor; crack tensor; multiple joint sets; rock mass

1 Introduction

Rock mass is a compound material that exists in specific geologic surroundings, including intact rocks and discontinuities, such as joints, fissures, and separations, forming a rather complex structure [1]. The existence of the discontinuity system makes the rock mass possess an obvious discontinuity, heterogeneity, and anisotropy [2], as shown in Fig. 1. In the first International Society for Rock Mechanics (ISRM) in 1966, Muller stated that “discontinuity and anisotropy are the most characteristic properties of the material rock and that the properties of jointed media depend much more upon the joints of the unit rock block system than upon the rock material” [3]. In response, BROWN stated in the 12th ISRM international congress “that does not mean to say that theoretical continuum mechanics in the fields of both elasticity and plasticity did not, and does not, have application to rock mechanics and rock engineering. But it does mean that answering Professor MULLER’s implicit question about the strength of a rock mass requires consideration of the mechanics of a discontinuum” [4]. The strong influence of discontinuities on the mechanical and hydraulic properties of rock mass is actually reflected on all types of engineering problems, such as the designs of tunnels, underground caverns, slopes, dams [5].

Currently, the treatment of the discontinuity system in numerical analyses can be classified into two categories. In the first category, the discontinuities are described explicitly if the amount of fractures in the analyzing domain is not large. This approach is represented mostly using the distinct element method (DEM) [6-9] and the discontinuous deformation analysis (DDA) [10-12], which concentrate on the blocks, discontinuities and their interaction. This method sacrifices the problem size since representations of individual blocks and fractures are costly in terms of computer memory and speed. Therefore, despite the popularity of the “discrete approach”, its applicability in solving practical problems still maintains a challenging task [13]. In addition, in areas where the rock mass contains an extremely large number of fractures compared to the engineering domain, it is impractical and impossible to mode every fracture. Furthermore, the mechanical behavior of the rock mass seems to be continuous or pseudo-continuous. Therefore, the equivalent continuum method is often adopted that assumes the global behavior of the rock mass can be described by the principles of continuum mechanics [14-16]. This method combines the deformation properties of fractures and intact rock in the form of parameters to establish an equivalent model for efficiently calculating and analyzing the deformation characteristics of the entire rock mass.

Fig. 1 Rock mass with discontinuities

In the continuum approach, the equivalent elastic mechanical parameters of the fractured rock mass constitute important input parameters for all analyses of the rock mass deformation behavior. Considerable efforts have been expended in the past for determining the equivalent elastic mechanical properties. The determination methods can be classified into field tests, empirical relationships, analytical methods, and numerical methods [17]. Field test is the most direct way to obtain the equivalent elastic parameters, but it is costly and often involves uncertainty errors related to the effects of hidden factures, control of boundary conditions, equipment, test site preparation, blasting damage, and interpretation of results. These factors lead to test data of mechanical behavior of the rock mass with great inaccuracies and scatterness [18-20].

Empirical methods establish certain empirical relationships on the basis of the rock mass classification or based on the characterization results [20-23]. Although this method has gained extensive popularity for practical applications of engineering design, especially in tunneling [23-28], it often elicits estimates that are too conservative for property characterizations, largely because it makes use of categorized parameters based on case histories. The main shortcoming of this approach is that it lacks a proper mathematical platform to establish constitutive models and ensure that the associated properties will not violate the second law of thermodynamics. Furthermore, the anisotropy in the properties cannot be properly represented in tensor form that is a basic condition of continuum mechanics.

With the rapid growth of computing capacity, numerical methods are attracting more attention to determine individual properties, such as the strength or deformability of the fractured rock mass [13, 17, 29]. The numerical approach has a certain advantage, in that, the influence of an irregular fracture system geometry and complex constitutive models of intact rock and fractures can be directly included in the derivation of the equivalent mechanical properties of the rock mass. However, this method could not explicitly identify the interaction relations between the intact rock and the fractures.

An analytical method, being a traditional and classical method type for studying the equivalent deformation properties of rock mass, is characteristic for its compactness, clarity, and directness [30-35]. Although studies on analytical methods are always based on the model of the rock mass with regular fracture systems, and although they cannot consider the interaction between the fractures and the blocks divided by the fractures, it is a very suitable method for the rock mass with regular multiple joint sets [35]. In their turn, multiple joint sets play an important role in the stability of rock engineering, such as in the case of columnar jointed rock mass [36]. For other methods, a complete analytic expression for the equivalent elastic constitutive model of rock mass is the foundation of the extended analysis of its deformation properties under the combined action of rock and fractures. Therefore, the analytical expression of the constitutive model of elastic deformation of the rock mass has an important place among the methods employed the equivalent continuum approach. However, at present, the analytical solution of the equivalent elastic deformation parameters is always obtained in planar models or is mainly fastened on the expression of the equivalent elastic modulus [30-31, 34-35]. Thus far, no research has provided a complete analytical expression for the equivalent elastic compliance tensor of rock mass in three-dimensional space, which restricts the rounded analysis for the space changing rules of its equivalent elastic properties.

The deformation properties of rock mass in space are closely related to the distribution of joints, which control the anisotropy of rock mass deformation. Consequently, in order to quantitatively study the equivalent deformation properties of rock mass, the most important aspect is the accurate description of the spatial distribution of joints. The crack tensor, proposed by ODA in 1982 [37], is a quantitative comprehensive index describing the spatially varying geometric distribution of cracks in the form of a tensor [38-39]. It provides a theoretical basis for the determination of the spatially varying deformation properties of rock mass. After the formulation of this tensor, an elastic stress–strain relation is formulated in terms of the second-order and fourth-order crack tensors [37, 40-43] that make it possible to take into account explicitly the effect of joints on the elastic behavior of rock mass. Nevertheless, the current elastic constitutive model, which is built on the basis of finite-order crack tensors, cannot elicit an accurate analytical description for the elastic deformation behavior of the rock mass with a complex fracture system, and requires higher-order crack tensors [38]. Crack tensors of ranks higher than two are not directly related to a clear image of the crack geometry and need complex mathematical calculations, which are difficult to understand and applied to engineering practice. Since the crack tensor is limited to the description of the geometric properties of the fracture system, this constitutive model cannot be used for the rock mass that has several joint sets possessing different deformation characteristics.

This paper presents a detailed and accurate derivation of the modified crack tensor for the determination of the equivalent elastic compliance tensor of the rock mass with multiple persistent joint sets. First, the crack tensor for the multiple persistent joint sets is modified into a second-order form to describe the spatial properties of the rock mass, including its geometric and mechanical properties. Subsequently, based on the eigenvalues and eigenvectors of the modified crack tensor, the full and accurate equivalent elastic compliance tensor of the rock mass with multiple persistent joint sets is obtained based on the theoretical deduction in three-dimensional space. The precise verification for each component of the compliance tensor using three-dimension distinct element code (3DEC) showed excellent equivalency from discontinuum to continuum. Finally, a comprehensive analysis is pursued for the spatial changing rules of the equivalent elastic parameters of the rock mass with a single persistent joint set.

This research lays the groundwork for the analysis of the equivalent elastic deformation characteristics of rock mass and provides a new thought process and methodology for an in-depth research in rock mass constitutive theory.

2 Modified crack tensor

2.1 Classic crack tensor

In 1982, ODA proposed a symmetric crack tensor, F, with an even order, expressed by Eq. (1). In effect, this equation is the tensor representation of the spatially varying geometric distribution of the cracks in terms of the tensor product of the cracks’ orientation vectors.

              (1)

where ρ is the volume density of the cracks defined by ρ=m^(V)/V; m^(V) is the number of cracks whose centroids are located inside a volume V; r is the diameter of crack, whose shape is assumed to be equivalent to a thin disc; n is the unit direction vector of the crack; E(n, r) is the joint probability density function of n and r; and Ω is the entire solid angle (equal to 4π). If the information for each crack is known, Eq. (1) can be rewritten in the form as

                    (2)

where the superscript k represents the serial number of the cracks.

On the basis of statistical theory, the crack tensor combines the cracks density, size, and orientation through multiplication and tensor product to allow implementation of the decomposition of the geometric features in space. The crack tensor, as a comprehensively quantitative index that expresses the geometric distribution of cracks, provides an establishment for a more effective and complete analysis of the theory related to cracks in space [44-47].

2.2 Modified crack tensor

The spatial deformation properties of rock mass are closely related to the density, size, orientation, and deformation stiffness of the cracks. With the increase of crack density and size or the decrease of the deformation stiffness, it becomes easier for the rock mass to deform. Therefore, the crack tensor is modified based on its initial form reflecting only the geometric features of cracks, for the purpose of describing the characteristics of spatial deformation of the rock mass. The modified crack tensor, shown in Eq. (3), is established based on the deformation characteristics of the cracks. It is a second-order tensor that takes into consideration the factors of the cracks that affect the rock mass deformation.

                             (3)

where s^(k) is the area of the kth crack obtained through s^(k)=π(r^(k))²/4; and JF is the stiffness coefficient of the crack. If the stiffnesses k_n0 and k_s0 of any crack whose JF value is unity are taken to be the reference values, the JF values of other cracks are calculated based on the algorithm, JF=k_n/k_n0=k_s/k_s0, assuming that the stiffness ratio of the cracks is identical; E(n, r, JF) is the joint probability density function of n, r, and JF. JF^(k) is the stiffness coefficient of the kth crack.

It can be intuitively said that the detail of the geometry and deformation characteristics of the cracks can be better represented if the higher-rank tensors are considered. However, the second-order modified crack tensor is enough to describe the space geometry and deformation characteristics of the crack systems precisely with one crack set, and with two or three crack sets that are orthogonal to each other. More importantly, the modified crack tensors of ranks higher than two are not directly related to a clear image of the crack geometry in three-dimensional space. On the premise of making comprehensive consideration, the second-order modified crack tensor is adopted as the theoretical tool to allow the study of the elastic stress–strain relation of the rock mass with multiple persistent joint sets.

In the geological exploration stage of rock engineering, joints in rock mass are generally grouped according to their geometric characteristics for refining and simplifying the joint system [1, 48], which is conducive to preferably grasp and examine the joints controlling the deformation of the rock mass at the macro level. Therefore, in order to conveniently utilize the statistical results of preferred joints, the crack tensor is modified into the form expressed with joint sets. This is in accordance to the spatial distribution figure of multiple persistent joint sets in the columnar statistical area, as shown in Fig. 2. For multiple persistent joint sets, the modified crack tensor can be expressed in accordance to

                                 (4)

where q is the number of joint sets; p is the serial number of joint sets; N^(p) is the number of joints in the pth set; r ^(p) is the diameter of joints in the pth set; JF ^(p) is the stiffness coefficient of joints in the pth set; n^(p) is the unit direction vector of joints in the pth set; S(p) m is the spacing of joints in the pth set; λ^(p) is the angle between the normal vector of joints in the pth set and the scanning line; and L is the length of the scanning line.

2.3 Basic properties of modified crack tensor

Since the components of the modified crack tensor do not have an explicit meaning in three-dimensional space, the eigenvalues and eigenvectors are computed to orthogonalize the equivalent deformation properties of the cracks. The eigenvalues and eigenvectors possess the following properties:

1) The modified crack tensor is a symmetric tensor, Fm ij=Fm ji, and has three independent and mutually orthogonal eigenvectors. They are the principal directions of the deformation of cracks.

2) The zero-order tensor Fm 0, the first invariant of the modified crack tensor and the sum of eigenvalues of the modified crack tensor are equal, as shown by Eq. (5). Appendix A illustrates the mathematical proof. and the sum of and are associated with the spacing and the elastic stiffness of the cracks and are irrelevant to the orientation of the persistent cracks. They comprehensively elicit an expression to the holistic deformation ability of the cracks.

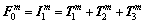                                            (5)

3) The eigenvectors of the modified crack tensor change with the orientation, size, spacing, and elastic stiffness. They equivalently orthogonalize the deformation properties of the cracks in the principal directions. The relative magnitude of the eigenvalues embodies the relative deformation ability of the cracks in the principal directions and the anisotropic degree of the equivalent elastic deformation of the rock mass. With the addition of the modified tensors of the multiple crack sets, the bias of the eigenvectors towards the principal directions is influenced by the comprehensive deformation properties of the multiple crack sets, which is indicative of the spatial deformation characteristics of the cracks.

Fig. 2 Multiple persistent joint sets in columnar statistical area

4) The eigenvector corresponding to the non-zero eigenvalue of the orientation tensor that is obtained by the tensor product of the orientation vector of a single crack set is identical to the orientation vector of the crack set, and the eigenvalue is equal to the squared length of orientation vector. When the orientation vector is expressed in a unit vector form, the eigenvalue is identical to the length of the orientation vector. Therefore, the eigenvalues and eigenvectors of the modified crack tensor of a single crack set can accurately describe the principal features of this crack set in a mathematical sense.

5) Similar to the stress tensor case, the invariant of the second deviatoric modified crack tensor reflects the deformation difference in the principal direction, namely, the invariant can embody the anisotropic degree of the spatial deformation ability of the cracks to some extent.

In order to accurately determine the analytic solution of the equivalent elastic compliance tensor of the rock mass with multiple persistent joint sets, the entire derivation process is based on the eigenvalues and eigenvectors of the modified crack tensor with a single crack set in terms of the properties of the modified crack tensor and its eigenvalues and eigenvectors mentioned above. The compliance tensor of the rock mass with multiple persistent crack sets is then obtained by means of the superposition principle.

3 Equivalent elastic compliance tensor of rock mass

Based on the definition of a modified crack tensor and in order to accurately analyze the analytical relation of the elastic stress and strain of the rock mass with multiple persistent joint sets, the following theoretical assumptions are introduced:

1) The intact rock is an isotropic linear elastic body.

2) The deformation of the joints adheres to the linear elastic constitutive relations.

3) The stiffness ratio of each joint set is equal.

4) The elastic deformation of the rock mass is a superposition deformation of the joints and the intact rock.

The eigenvectors and eigenvalues of the modified crack tensor of a single crack set, as described by Eq. (6) and Eq. (7), can exactly express the principal deformation orientations and the corresponding deformation abilities of the crack system in space. The establishment of the modified crack tensor is based on the spatial deformation characteristics of the cracks. Therefore, similar to the form of the elastic compliance tensor of the rock mass with three mutually orthogonal persistent cracks deduced by AMADEI and GOODMAN [49], the eigenvalues of the modified crack tensor are used to denote the equivalent elastic compliance tensor of the rock mass with a single crack set in the principal deformation directions, as denoted by Eq. (8).

                                                      (6)

                                              (7)

  (8)

where E, ν, and G are the elastic modulus, Poisson ratio and shear modulus of the intact rock, respectively. The symbols k_n0 and k_s0 are the normal and shear stiffnesses of the fiducial crack set, respectively; Tms 1, Tms 2, and Tms 3 are the three eigenvalues of the modified crack tensor of a single crack set; v₁, v₂, and v₃ are the three eigenvectors corresponding to the eigenvalues; is the equivalent elastic compliance tensor in the principal deformation direction and the corresponding stress and strain components of in matrix form are =[σ_xx', σ_yy', σ_zz', σ_yz', σ_xz', σ_xy']^T, =[ε_xx', ε_yy', ε_zz', ε_yz', ε_xz', ε_xy']^T. is defined in the local coordinate system composed by the three eigenvectors of the modified crack tensor. Therefore, it is indispensable to transform into the equivalent elastic compliance tensor D in the global coordinate system.

Suppose that oxyz represents the local coordinate system composed by the eigenvectors, and that OXYZ represents the global coordinate system. The stress and strain tensor are denoted by and in OXYZ, respectively, and in oxyz are denoted by and . The direction cosines of the X-axis along the x, y, and z axes are denoted by l₁, m₁, and n₁, respectively, the direction cosines of the Y-axis along the x, y, and z axes are denoted by l₂, m₂, and n₂, respectively, and the direction cosines of the Z-axis along the x, y, and z axes are denoted by l₃, m₃, and n₃, respectively. The congruent relationship between the eigenvectors v₁, v₂, v₃ and the base vectors e₁, e₂, e₃ of the global coordinate system is determined by the corresponding relation between the stress and strain components (associated to the base vectors) and the eigenvalues (related to the eigenvectors). From Eq. (8), v₁, v₂, v₃ respectively correspond to e₁, e₂, e₃. The conversion matrix R of the stress and strain tensors from the local into the global coordinate system could then be calculated using the direction cosines, as denoted by Eq. (9). The equivalent elastic compliance tensor of the rock mass with a single crack set in the global coordinate system is obtained by Eq. (10).

R= (9)

                                                                  (10)

Finally, according to the basic assumptions, the equivalent elastic compliance tensor of the rock mass with multiple persistent crack sets can be computed based on the superposition principle.

The specific rock mass model shown in Fig. 3 is introduced to calculate the analytic solution of the equivalent elastic compliance tensor of the rock mass with multiple persistent joint sets. In three-dimensional space, the X, Y, and Z axes represent the East, North, and up in geographical space, respectively. The normal vector n^(p) of the pth joint set is expressed with (cosα^(p), cosβ^(p), cosλ^(p)), in which α^(p), β^(p), and λ^(p) are the angles between n^(p) and X, Y, and Z axes, respectively, and within the range [0, 2π]. Figure 3 only shows the rock mass with the pth joint set, with a spacing normal stiffness k_n0 and shear stiffness k_s0, and a corresponding stiffness coefficient JF^(p) for the single joint set is equal to unity.

Fig. 3 Rock model with a single joint set in three-dimensional space

According to the analysis process of the equivalent elastic compliance tensor described above, the equivalent elastic compliance tensor of the rock mass with multiple persistent joint sets for the specific model can be deduced following these steps.

1) Calculate the modified crack tensor of the single joint set.

2) Compute the eigenvalues and eigenvectors of the modified crack tensor.

3) Establish the equivalent elastic compliance tensor in the principal deformation directions by substituting the eigenvalues into Eq. (8).

4) Calculate the transition and inverse matrices of the stress and strain tensors according to the corresponding relationship of the eigenvectors and the base vectors.

5) Obtain the equivalent elastic compliance tensor of the rock mass with a single joint set using Eq. (10).

6) Calculate the equivalent elastic compliance tensor of the rock mass with multiple persistent joint sets based on the superposition principle.

By substituting the specific parameters of the rock mass model into the derivation steps listed above, the analytic solution of the equivalent elastic compliance tensor of the rock mass with multiple persistent joint sets is obtained, as indicated by Eq. (11). The specific derivation process is listed in “Appendix B”. The equivalent elastic compliance tensor is symmetric when the shear strain components of the strain tensor are replaced by the engineering shear strains, thereby satisfying the second law of thermodynamics. It is indicative of the rationality of the derivation method and the result of the equivalent elastic compliance tensor on the basis of the modified crack tensor from the energy point of view.

 (11)

4 Verification of equivalent elastic compliance tensor

4.1 Verification of main components of compliance tensor with laboratory experiments

To investigate the deformation and strength anisotropy of the rock types Asan gneiss, Boryeong shale, and Yeoncheon schist, uniaxial compression tests have been conducted for the three kinds of rocks at different angles between the loading direction and the transverse isotropic plane [51]. The abstract model of the rocks is shown in Fig. 4.

The transverse isotropic plane is analogous to the joint plane defined under the basic assumptions. Based on Ref. [51], Table 1 summarizes the equivalent elastic modulus of the three types of rocks of the different experimental groups, shown in Fig. 5. They are used for the verification of the main components D_ii(i=1, 2, 3) of the compliance tensor, as expressed by Eq.(12).

             (12)

where θ is the angle between the normal vector of the isotropic plane and the direction of investigation of the elastic modulus in Fig. 5.

The average values of the elastic modulus of gneiss, shale, and schist in the directions θ=0°, 30°, 90° as the learning values are substituted into the Eq. (12) to calculate the values of E, S_mk_n, and S_mk_s. Based on Eq. (12) and given the known values of the parameters, the theory curves of the equivalent elastic modulus are obtained. The elastic modulus in the direction θ=15°, 45°, 60°, 75° as the testing values are compared with the corresponding theoretical values. The comparison results are shown in Fig. 5 and reveal that the equivalent elastic modulus can better describe the experiment data. This is a good verification outcome of the main components of the equivalent elastic compliance tensor with the experimental measures.

Fig. 4 Abstract model of Asan gneiss, Boryeong shale, and Yeoncheon schist rocks

Table 1 Elastic modulus of Asan gneiss, Boryeong shale, and Yeoncheon schist rock types

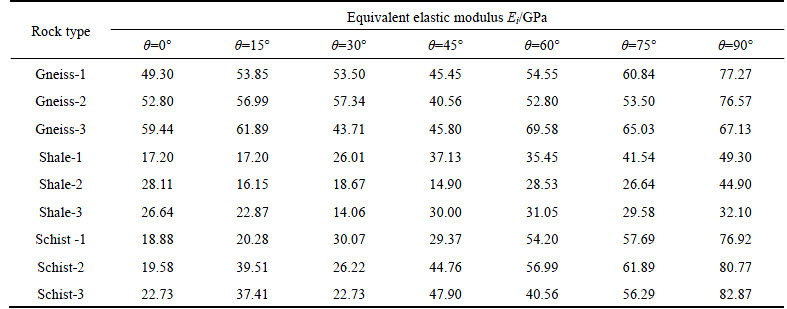
Fig. 5 Comparison between theoretical equivalent elastic modulus and experimental results for Asan gneiss (a), Boryeong shale (b), and Yeoncheon schist rocks (c)

Fig. 6 Numerical experiments for verification of equivalent elastic compliance tensor:

4.2 Numerical experiments modeling and verification by 3DEC

Owing to the limited loading technology of force and displacement, and the finite monitoring precision of laboratory experiments, it is arduous to reliably verify each component of the equivalent elastic compliance tensor through triaxial or shear tests. Therefore, the numerical experiment method with 3DEC is adopted for the verification [52-54]. 3DEC, as three-dimensional discrete element software, can expediently build a rock mass model with explicit multiple joint sets, and accurately simulate the deformation behavior of the intact rock and joints when the assumptions proposed above for the analytic derivation of the equivalent elastic compliance tensor are satisfied.

4.2.1 Numerical experimental schemes of 3DEC

In order to verify each component of the equivalent elastic compliance tensor, numerical experiments combining scheme 1 and scheme 2 are implemented to the rock block model [52]. Scheme 1 is set and used for the verification of the components relevant to normal stress components, and scheme 2 is set and used for the verification of components relevant to shear stress components.

In scheme 1, the rock block was first subjected to an isotropic compressive stress in the three perpendicular directions x, y, and z. The stress in the third direction was then increased by applying a constant velocity of 0.05 m/s, and the stresses of the other two boundaries remain constant, as shown in Fig. 6(a). This was repeated in each of the three perpendicular directions. Figure 6(b) explains scheme 2. The rock block was first subjected to an isotropic compressive stress in the three perpendicular directions x, y, and z. The rock block was then subjected to an increasing shear stress, as shown in Fig.6(b). On each block face eighty-one points are equally distributed to monitor the coordinate values and the stresses of each block face, as shown in Fig. 6(c).

During the loading process in schemes 1 and 2, coordinate values and stress components of the monitored points along the x, y, and z directions are recorded simultaneously on each face, in order to calculate each component of the equivalent compliance tensor of the block. The average coordinate values of the monitored points on the same face along the x, y, and z directions represent the coordinate values of each face in the corresponding directions. The symbolic representation for the coordinate values of each face in the x, y, and z directions are illustrated in Appendix C and the meaning of the symbols is shown in Fig. 7(b). This figure only depicts the deformation of a face in the x and z directions, when the applied loading is along the z direction. The other symbols can be comprehended using the same analogy.

The faces of the rock model are projected on each coordinate plane to allow the calculation of the equivalent strain components, as shown in Fig. 7(a). Because of the joints, the rock model will produce the superimposed deformation of the geometrical morphology exhibited in Fig. 7(b) and Fig. 7(c) [17], under the different loading conditions. According toFigs. 7(b) and (c) (the geometrical deformation forms of the other faces of the rock model can be comprehended based on the same analogy), the equivalent normal strain and shear strain components of the rock model are calculated using Eqs. (13a-c) and Eqs. (14a-c), respectively, on the basis of the average coordinate values of each face, as shown in Appendix C.

                              (13a)

                            (13b)

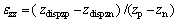                              (13c)

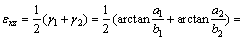
                               (14a)

                      (14b)

                            (14c)

Fig. 7 Schematic diagram of normal and shear strain evaluations:

4.2.2 Implementation of numerical experiments

According to schemes 1 and 2, numerical tests are carried out on three rock models cut by one set, two sets,and four sets of persistent joints, respectively. The specific parameters of the joints are shown in Table 2. The elastic modulus and Poisson’s ratio of the intact rock are 40 GPa and 0.25, respectively.

For the rock model with persistent joints, the ratio of the model size and the joint spacing is the main factor for controlling the spatial form of the rock mass. To eliminate the influences of the number of mesh units on the stability of the numerical results, the minimum ratio of the model size and joint spacing of the rock model is analyzed by changing the ratio of the model size and joint spacing of the single joint set in rock model 1. In this model, the joint spacing remains unchanged and the model size gradually increases. The numerical solutions of each component of the equivalent elastic compliance tensor are computed using numerical tests with the rock model at different sizes. The corresponding analytical solutions are calculated from Eq. (11). Figure 8 demonstrates the change rules of the deviations between the numerical and the analytical solutions of the main components at increasing ratios. The analyses results of Fig. 8 suggested that when a/S_m≥8, the fluctuation of the numerical solutions is well controlled in regard to the accuracy of the numerical calculation. The deviations are within 1% and meet the requirements of numerical validation. Hence, the size of the rock model for the numerical tests is determined to be 1.6 m×1.6 m×1.6 m when the joint spacing is 0.2 m.

4.2.3 Comparison of analytical and numerical solutions

The numerical and analytical solutions of the equivalent elastic compliance tensors of every rock model are calculated separately, and the results are shown in Table 3. Comparative analysis indicates that the numerical and analytical solutions are nearly identical. This is a favorable verification of the correctness and appropriateness of the analytical solutions and of the corresponding derivation of the equivalent elastic compliance tensor of the rock mass with multiple persistent joint sets. Meanwhile, the order of magnitude of the components relevant to the interaction and Chentsov coefficients in the compliance tensor is comparable to the main components, such as D₁₁, D₄₄, D₁₂. This illustrates that the influence of normal stresses on shear strains and the shear stresses on normal strains cannot be ignored for the analysis of the elastic deformation of rock mass when joints exist. The equivalent elastic compliance tensor presents the analytical solutions of the components relevant to the interaction and Chentsov coefficients, which provides the analytic foundation of a comprehensive and elaborate research of the equivalent elastic deformation properties of rock mass.

Table 2 Rock models and parameter values of joints used in numerical experiments

Fig. 8 Minimum ratio of model size and joint spacing of rock model analysis diagram

Table 3 Comparison of analytical and numerical solutions of equivalent elastic compliance tensor (Gray and blue histograms represent numerical and analytic solutions, respectively)

5 Analysis of properties of equivalent elastic parameters

The equivalent elastic properties of rock mass with multiple persistent joint sets are obviously anisotropic, which implies that the equivalent elastic parameters of the theoretical model are different in different directions. To account for the use of the superposition principle for the above theoretical derivation, it is necessary to determine the spatial change rules of the equivalent elastic parameters for the rock mass with a single joint set that forms the basis of the analysis of the spatial elastic properties of rock mass with additional joint sets. Accordingly, the pivotal equivalent elastic parameters, namely, the equivalent elastic modulus and equivalent Poisson’s ratio, and equivalent shear modulus, are systematically analyzed and discussed here. The general elastic constitutive equation for rock mass is shown in Eq. (15) [55].

 (15)

where E_x, E_y and E_z are the elastic modulus along the X, Y and Z directions, respectively; G_yz, G_xz and G_xy are the elastic shear modulus along the YZ, XZ and XY planes, respectively; ν_xy, ν_yx, ν_xz, ν_zx, ν_yz and ν_zy are the Poisson ratios; ν_ij represents the ratio of the normal strain along j direction and the normal strain along i direction considering the action of stress along the i direction. Moreover, η_x,yz, η_y,yz, η_z,yz, η_x,xz, η_y,xz, η_z,xz, η_x,xy, η_y,xy and η_z,xy are the interaction coefficients of the mutual influence of the first kind; η_i,jk represents the influence of the shear stress along the jk direction on the normal strain along the i direction; η_yz,x, η_yz,y, η_yz,z, η_xz,x, η_xz,y, η_xz,z, η_xy,x, η_xy,y and η_xy,z are the interaction coefficients of the mutual influence of the second kind; η_ij,k represents the influence of the normal stress along the k direction on the shear strain along the ij direction; μ_yz,xz, μ_yz,xy, μ_xz,yz, μ_xz,xy, μ_xy,yz and μ_xy,xz are the Chentsov coefficients; μ_ij,kl represents the influence of the shear stress along the kl direction on the shear strain along the ij direction.

The equivalent elastic modulus and equivalent Poisson's ratio can be expressed by Eqs. (16a-c) and Eqs. (17a-f), respectively, according to the general constitutive model shown in Eq. (15) and the equivalent elastic compliance tensor for the rock mass with a single joint set shown in Eq. (29). The analytical expressions for the equivalent shear modulus, interaction and Chentsov coefficients are included in Appendix D.

                     (16a)

                    (16b)

                      (16c)

                    (17a)

                    (17b)

                     (17c)

                     (17d)

                     (17e)

                     (17f)

For the sake of concise and clear expression of the spatial orientation of the joints, the normal vectors of joints are adopted. A single persistent joint set consists of two normal vectors in the opposite directions. For a complete analysis of the spatial performance of the change rules of the equivalent elastic parameters, the parameters of the rock mass are calculated in both of the opposite directions of the joints to show the deformation properties of the rock mass with a single joint set. The required parameter values are shown in Table 4. The controlling variables method is used to solve the spatial changing rules of the equivalent elastic parameters, according to the values listed in Table 4 where the values indicated in bold are the basic parameter values. The influences of the attributes of the intact rock and joints on the equivalent elastic parameters of the rock mass are investigated by means of changing the corresponding attribute values, while the basic parameters are assigned to the other attributes. When studying the influences of the elastic stiffness of joints on the equivalent elastic parameters, the stiffnesses are varied according to the stiffness ratios and the basic values of stiffnesses.

Figure 9 shows the changing rule of the equivalent elastic modulus along the Z direction based on the variation of the joint spatial orientation in spherical coordinates. It is obtained by substituting the basic parameters of Table 4 into Eq. (16c). The position vectors from the origin to the points on the curved surface determine the normal vectors of the joint sets, and the angles between the normal vector and the X, Y, Z axes are α, β, and λ, respectively. The color of the surface represents the magnitude of the equivalent elastic modulus. The joint orientations of four specific points on the curved surface are depicted in Fig. 9 in an effort to vividly illustrate the meaning and significance of the figure. Preliminary analysis indicates that the changing rules of the equivalent elastic parameters of the rock mass with a single joint set have a spatial symmetry. Therefore, the focus of the descriptions and discussions is placed on the changing rules in the first quadrant space. In addition, the equivalent elastic parameters in different directions, such as E_x, E_y, and E_z, are described by similar analytic expressions. Consequently, E_z, and ν_xy are chosen as the representative parameters for revealing the spatial changing rules of the equivalent elastic parameters of the rock mass.

Table 4 Parameter values of intact rock and joints

Fig. 9 Changing rules of E_z for illustration of spatial curved surface figure

5.1 Equivalent elastic modulus

According to Eq. (16c), the equivalent elastic modulus of the rock mass is related to the elastic modulus of the intact rock, spacing, normal stiffness, shear stiffness, and the orientation of joints. For example, the changing rules for E_z are shown in Figs. 10 and 11. Additionally, the detailed analysis of the influencing rules is described below.

Fig. 10 Spatial changing rules of E_z at different E and S_m values

Fig. 11 Spatial changing rules of E_z at different k_n and k_s values

1) The equivalent elastic modulus of the rock mass increases when E, S_m, k_n, and k_s increase. When the normal vector of the joints and the direction at which the equivalent elastic modulus is investigated are perpendicular to each other, the equivalent elastic modulus is identical to the elastic modulus of the intact rock which is the maximum equivalent elastic modulus and irrelevant to the properties of the joints.

2) The equivalent elastic modulus only changes with the orientation angle (α, β, or λ) between the normal vector of the joint set and the direction at which the equivalent elastic modulus is investigated, and is unrelated to any of the other angles.

3) The changing trend of the equivalent elastic modulus with the orientation angle is only related to the stiffness ratios of the joints. In the first quadrant, at decreasing stiffness ratios, the changing trend of the equivalent elastic modulus that decreases first and then increases turns into a gradual increase when the orientation angle increases. The entire spatial variation pattern changes from convex to concave. The stiffness ratio determines the orientation of the joints that corresponds to the minimum equivalent elastic modulus.

5.2 Equivalent Poisson ratio

According to Eq. (17b), the equivalent Poisson ratio of the rock mass is related to the Poisson’s ratio and the elastic modulus of the intact rock, spacing, normal stiffness, shear stiffness, and the orientation of the joints. In the case of ν_xy, for example, its changing rules are shown in Figs. 12 and 13. Correspondingly, the detailed analysis of the influencing rules is described as below.

Fig. 12 Spatial changing rules of ν_xy at different values of ν, E, and S_m

Fig. 13 Spatial changing rules of ν_xy at different k_n and k_s values

1) The equivalent Poisson ratio grows in direct proportion to ν increases.

2) The changing rules of the equivalent Poisson ratio with respect to E and S_m elicit a threshold effect with regard to the orientation angles in the plane under investigation. The critical value, arcsin{[ν/(1-ν)]·[k_s/ (k_n-k_s)]}^0.5, is achieved once the equivalent Poisson ratio becomes equal to the Poisson's ratio of the intact rock. When the angle between the normal vector and the coordinate axis in the plane under investigation is equal to the critical value, the equivalent Poisson's ratio remains unchanged as E and S_m vary. When the angle becomes larger than the critical value, the equivalent Poisson ratio increases with increase in E and decreases with increase in S_m. When it is less than the critical value, it decreases as E increases and increases as S_m increases.

3) The equivalent Poisson ratio increases with increasing k_n and decreases with increasing k_s. The changing rules of the equivalent Poisson ratio are only dependent on the stiffness ratio. In the plane under investigation, at a decreasing stiffness ratio, the changing trend of the equivalent Poisson ratio that increases first and then decreases turns into the trend that decreases first and then increases, when the orientation angle between the normal vector of the joint and the coordinate axis of the plane under investigation increases.

6 Discussions and conclusions

This work presents an analytical description in a systematic way for deriving the complete equivalent elastic properties of rock mass with multiple persistent joint sets, from the establishment of the modified crack tensor to the derivation of the equivalent elastic compliance tensor, the experimental verification, and finally, the analysis of the elastic properties of the elastic parameters. The main discussions and conclusions from the present study are summarized as follows:

1) The modified crack tensor provides a comprehensive consideration of the geometric characteristics (size, density, orientation) and the mechanical properties of joints to reflect the spatial elastic deformation of the multiple persistent joint sets.

The principal deformation direction and the corresponding deformability of a single joint set can be accurately formulated by the modified crack tensor. The modified crack tensor provides a new theoretical way to study the equivalent elastic compliance tensor of the rock mass with multiple persistent joint sets in three-dimensional space. Therefore, the equivalent elastic compliance tensor can be obtained based on the eigenvalues and the eigenvectors of the modified crack tensor with a single crack set. The compliance tensor presents the complete analytic solution of the equivalent elastic compliance tensor that contains the primary equivalent elastic parameters, such as elastic modulus, and Poisson’s ratio which many researchers focus on, and the interaction and Chentsov coefficients in the global coordinates. The symmetry of the equivalent compliance tensor and the verification results of laboratory and numerical experiments fully illustrate the rationality and validity of the equivalent compliance tensor. At the same time, it is more comprehensive and convenient to consider the geometric and mechanical properties of the cracks and to apply the modified crack tensor in the research of the constitutive theory of the rock mass, which provides new research ideas and methods.

2) The spatially dependent changing rules of the main equivalent elastic parameters of the rock mass with a single joint set reveal the universal law of the parameters of the stratified rock mass in accordance to the basic assumptions. The properties of the intact rock and the joints affect the equivalent deformation properties of the entire rock mass. The specific performance elicited is that the stiffness ratios of joint sets affect the changing trends and the extreme values of the equivalent elastic parameters with changes in the spatial orientation of the joint set. The absolute magnitude of the elastic modulus and Poisson ratio of the intact rock, and the spacing and elastic stiffness of joints, only exerts an influence on the magnitude of the equivalent elastic parameters, and does not change the trend with changes in the spatial orientation of joints.

3) The research provides the base form of the rock mass equivalent elastic parameters, which don't take into account the nonlinear deformation characteristics of the joints and the interaction between the joints. For the specific project, the extension research can be made base on the base form to meet more complex joint properties.

Appendix

Appendix A: The mathematical proof for Eq. (5)

               (18)

               (19)

Appendix B: The solution process for Eq. (11)

(1) The modified crack tensor of a single crack set is

(20)

(2) Compute the eigenvalues and eigenvectors of the modified crack tensor

a) The eigenvalues are represented by the following equation:

                                                    (21a)

                                                                    (21b)

                                                                     (21c)

b) The corresponding eigenvectors are given by the equations:

                    (22a)

          (22b)

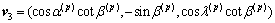 (22c)

(3) Establishing the equivalent elastic compliance tensor in the principal deformation directions is achieved by substituting the eigenvalues into Eq. (8)

      (23)

(4) Compute the transformation matrix and the inverse matrix of the stress and the strain tensors, according to the corresponding relation of the eigenvectors and the base vectors of the global coordinate system.

a) Base vectors of global coordinate system

                                       (24a)

                                       (24b)

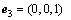                                       (24c)

b) Corresponding eigenvectors

                       (25a)

            (25b)

         (25c)

c) Direction cosines

                                 (26a)

                       (26b)

                         (26c)

                                (26d)

                                     (26e)

                               (26f)

                                  (26g)

                         (26h)

                            (27i)

d) Calculate the transformation matrix using Eq. (9)

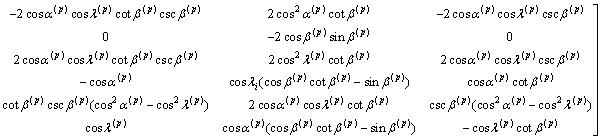(27)

e) Inverse the transformation matrix

               (28)

(5) Calculate the equivalent elastic compliance tensor of rock mass with a single joint set using Eq. (14)

(29)

(6) Calculate the equivalent elastic compliance tensor of the rock mass with multiple persistent joint sets, according to the superposition principle.

(30)

Appendix C: Symbol explanation for average coordinates for every face of the rock mass model

Appendix D: The analytic expressions of the equivalent shear modulus, interaction and Chentsov coefficients

Equivalent shear modulus

(31a)

(31b)

(31c)

Interaction coefficients

              (31a)

         (31b)

          (31c)

          (31d)

              (32e)

           (32f)

         (32g)

         (32h)

             (32i)

             (32a)

          (32b)

            (32c)

         (32d)

                (32e)

            (32f)

          (32g)

            (32h)

                 (32i)

Chentsov coefficients

(33a)

(33b)

(33c)

(33d)

(33e)

(33f)

References

[1] BRADY B H. Rock mechanics for underground mining [M]. New York: Springer, 2004.

[2] PRIEST S D. Discontinuity analysis for rock engineering [M]. New York: Springer, 1993.

[3] MLLER L. Address to the opening session[C]//Proc 1st Congr, Int. Soc. Rock Mech, 1967: 80-83.

[4] BROWN E T. Fifty years of the ISRM and associated progress in rock mechanics[C]//QIAN Q, ZHOU X Y, ed. Proc 12th ISRM Cong on ‘Rock Mechanics’. Beijing, China: International Society for Rock Mechanics, 2011: 29-45.

[5] EINSTEIN H H, VENEZIANO D, BAECHER G B, OREILLY K J. The effect of discontinuity persistence on rock slope stability[J]// International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, Pergamon, 1983, 20(5): 227-236.

[6] CUNDALL P A. A computer model for simulating progressive, large scale movements in blocky rock systems Proceedings of the international symposium on rock fractures[C]. International Society for Rock Mechanics, 1971: 1-12.

[7] CUNDALL P A. Formulation of a three-dimensional distinct element model—Part I. A scheme to detect and represent contacts in a system composed of many polyhedral blocks[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics, 1988, 25(3): 107-116.

[8] LEMOS J V, HART R D, CUNDALL P A. A generalized distinct element program for modelling jointed rock mass[C]//International Symposium on Fundamentals of Rock Joints. Bjokliden:[Lulea Tekniska Universitet]. 1985: 335-343.

[9] HART R, CUNDALL P A, LEMOS J. Formulation of a three-dimensional distinct element model—Part II. Mechanical calculations for motion and interaction of a system composed of many polyhedral blocks[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics, 1988, 25(3): 117-125.

[10] CUNDALL P A. Distinct element models of rock and soil structure[J]. Analytical and Computational Methods in Engineering Rock Mechanics, 1987, 4: 129-163.

[11] SHI G H. Discontinuous deformation analysis: A new numerical model for the statics and dynamics of deformable block structures[J]. Engineering Computations, 1992, 9(2): 157-168.

[12] JING L. Formulation of discontinuous deformation analysis (DDA)—An implicit discrete element model for block systems[J]. Engineering Geology, 1998, 49(3): 371-381.

[13] MIN K B, JING L. Numerical determination of the equivalent elastic compliance tensor for fractured rock masses using the distinct element method[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(6): 795-816.

[14] ESPOSITO C, MARTINO S, MUGNOZZA G S. Mountain slope deformations along thrust fronts in jointed limestone: An equivalent continuum modelling approach[J]. Geomorphology, 2007, 90(1): 55-72.

[15] AYDAN , JEONG G C, SEIKI T, AKAGI T. A comparative study on various approaches to model discontinuous rock mass as equivalent continuum[C]//The 2nd Int Conf on Mechanics of Jointed and Fractured Rock. Vienna: ICMJFR, 1995: 569-574.

[16] MIN K B. Fractured rock masses as equivalent continua-A Numerical Study[D]. Stockholm: Royal Institute of Technology (KTH), 2004.

[17] YANG J P, CHEN W Z, DAI Y H, YU H D. Numerical determination of elastic compliance tensor of fractured rock masses by finite element modeling[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 70: 474-482.

[18] BIENIAWSKI Z T. Determining rock mass deformability: experience from case histories[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics, 1978, 15(5): 237-247.

[19] PALMSTRM A, SINGH R. The deformation modulus of rock masses—Comparisons between in situ tests and indirect estimates[J]. Tunnelling and Underground Space Technology, 2001, 16(2): 115-131.

[20] HOEK E, DIEDERICHS M S. Empirical estimation of rock mass modulus[J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(2): 203-215.

[21] CAI M, KAISER P K, UNO H. Estimation of rock mass deformation modulus and strength of jointed hard rock masses using the GSI system[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(1): 3-19.

[22] SONMEZ H, GOKCEOGLU C, ULUSAY R. Indirect determination of the modulus of deformation of rock masses based on the GSI system[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(5): 849-857.

[23] BARTON N. Some new Q-value correlations to assist in site characterisation and tunnel design[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(2): 185-216.

[24] GENIS M, BASARIR H, OZARSLAN A, BILIR E, BALABAN E. Engineering geological appraisal of the rock masses and preliminary support design, Dorukhan Tunnel, Zonguldak, Turkey[J]. Engineering Geology, 2007, 92(1): 14-26.

[25] BIENIAWSKI Z T. Tunnel design by rock mass classifications[D]. Pennsylvania: Pennsylvania State Univ University Park Dept of Mineral Engineering, 1990.

[26] CARRANZA-TORRES C, FAIRHURST C. Application of the convergence-confinement method of tunnel design to rock masses that satisfy the Hoek-Brown failure criterion[J]. Tunnelling and Underground Space Technology, 2000, 15(2): 187-213.

[27] BARTON N, LIEN R, LUNDE J. Engineering classification of rock masses for the design of tunnel support[J]. Rock Mechanics, 1974, 6(4): 189-236.

[28] HOEK E, BROWN E T. Practical estimates of rock mass strength[J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(8): 1165-1186.

[29] BIDGOLI M N, ZHAO Z, JING L. Numerical evaluation of strength and deformability of fractured rocks[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2013, 5(6): 419-430.

[30] GERRARD C M. Equivalent elastic moduli of a rock mass consisting of orthorhombic layers[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics, 1982, 19(1): 9-14.

[31] SALAMON M D G. Elastic moduli of a stratified rock mass[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics, 1968, 5(6): 519-527.

[32] SINGH B. Continuum characterization of jointed rock masses: Part I—The constitutive equations[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics, 1973, 10(4): 311-335.

[33] FOSSUM A F. Effective elastic properties for a randomly jointed rock mass[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics, 1985, 22(6): 467-470.

[34] AMADEI B. Importance of anisotropy when estimating and measuring in situ stresses in rock[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics, 1996, 33(3): 293-325.

[35] GERRARD C M. Elastic models of rock masses having one, two and three sets of joints[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics, 1982, 19(1): 15-23.

[36] JIANG Q, FENG X T, HATZOR Y H, HAO X J, LI S J. Mechanical anisotropy of columnar jointed basalts: An example from the Baihetan hydropower station, China[J]. Engineering Geology, 2014, 175: 35-45.

[37] ODA M. Fabric tensor for discontinuous geological materials[J]. Soils and Foundations, 1982, 22(4): 96-108.

[38] ODA M. Similarity rule of crack geometry in statistically homogeneous rock masses[J]. Mechanics of Materials, 1984, 3(2): 119-129.

[39] ODA M. A stereological study on crack geometry of discontinuous rock masses[C]//Proceedings of the First International Symposian for Science on Form. Tokyo: KTK Scientific Publisher, 1986: 183-189.

[40] ODA M. A method for evaluating the effect of crack geometry on the mechanical behavior of cracked rock masses[J]. Mechanics of Materials, 1983, 2(2): 163-171.

[41] ODA M, SUZUKI K, MAESHIBU T. Elastic compliance for rock-like materials with random cracks[J]. Soils and Foundations, 1984, 24(3): 27-40.

[42] ODA M, YAMABE T, ISHIZUKA Y, KUMASAKA H, TADA H, KIMURA K. Elastic stress and strain in jointed rock masses by means of crack tensor analysis[J]. Rock Mechanics and Rock Engineering, 1993, 26(2): 89-112.

[43] ODA M, KATSUBE T, TAKEMURA T. Microcrack evolution and brittle failure of Inada granite in triaxial compression tests at 140 MPa[J]. Journal of Geophysical Research: Solid Earth (1978–2012), 2002, 107(B10): ECV 9-1-ECV 9-17.

[44] GUVANASEN V, CHAN T. Upscaling the thermohydromechanical properties of a fractured rock mass using a modified crack tensor theory[J]. Elsevier Geo-Engineering Book Series, 2004, 2: 251-256.

[45] GAO Z, ZHAO J, YAO Y. A generalized anisotropic failure criterion for geomaterials[J]. International Journal of Solids and Structures, 2010, 47(22): 3166-3185.

[46] PIETRUSZCZAK S, LYDZBA D, SHAO J F. Modelling of inherent anisotropy in sedimentary rocks[J]. International Journal of Solids and Structures, 2002, 39(3): 637-648.

[47] PIETRUSZCZAK S, MROZ Z. On failure criteria for anisotropic cohesive-frictional materials[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(5): 509-524.

[48] JAEGER J C, COOK N G W, ZIMMERMAN R. Fundamentals of rock mechanics[M]. John Wiley & Sons, 2009.

[49] AMADEI B, GOODMAN R E. A 3-D constitutive relation for fractured rock masses[C]//Proceedings of the International Symposium on the Mechanical Behavior of Structured Media. Part B, Amsterdam: Elsevier, 1981: 249-268.

[50] NOORIAN BIDGOLI M, JING L. Anisotropy of strength and deformability of fractured rocks[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2014, 6(2): 156-164.

[51] CHO J W, KIM H, JEON S, MIN K B. Deformation and strength anisotropy of Asan gneiss, Boryeong shale, and Yeoncheon schist[J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 50: 158-169.

[52] WU Q, KULATILAKE P. REV and its properties on fracture system and mechanical properties, and an orthotropic constitutive model for a jointed rock mass in a dam site in China[J]. Computers and Geotechnics, 2012, 43: 124-142.

[53] CHENG D X, PAN W, LIU D A, FEN S R, GUO H F, DING E B. 3DEC modeling of equivalent mechanical parameters in anchored jointed rock mass[J]. Rock and Soil Mechanics, 2006, 27(12): 2127-2132.

[54] DI S J, XU W Y, NING Y, WANG W, WU G Y. Macro-mechanical properties of columnar jointed basaltic rock masses[J]. Journal of Central South University of Technology, 2011, 18: 2143-2149.

[55] S G. Theory of elasticity of an anisotropic elastic body[M]. New York: Holden-Day, 1963.

(Edited by DENG Lü-xiang)

Foundation item: Projects(41172284, 51379202) supported by the National Natural Science Foundation of China; Project(2013CB036405) supported by the National Basic Research Program of China; Project(2013BAB02B01) supported by the National Key Technologies R&D Program of China

Received date: 2015-02-27; Accepted date: 2015-06-05

Corresponding author: JIANG Quan, PhD, Professor; Tel: +86-27-87198805; E-mail: qjiang@whrsm.ac.cn