J. Cent. South Univ. Technol. (2010) 17: 363-371
DOI: 10.1007/s11771-010-0054-y 
Adaptive predictive functional control based on Takagi-Sugeno model and its application to pH process
SU Cheng-li(苏成利), LI Ping(李平)
School of Information and Control Engineering, Liaoning Shihua University, Fushun 113001, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2010
Abstract: In order to obtain accurate prediction model and compensate for the influence of model mismatch on the control performance of the system and avoid solving nonlinear programming problem, an adaptive fuzzy predictive functional control (AFPFC) scheme for multivariable nonlinear systems was proposed. Firstly, multivariable nonlinear systems were described based on Takagi-Sugeno (T-S) fuzzy models; assuming that the antecedent parameters of T-S models were kept, the consequent parameters were identified on-line by using the weighted recursive least square (WRLS) method. Secondly, the identified T-S models were linearized to be time-varying state space model at each sampling instant. Finally, by using linear predictive control technique the analysis solution of the optimal control law of AFPFC was established. The application results for pH neutralization process show that the absolute error between the identified T-S model output and the process output is smaller than 0.015; the tracking ability of the proposed AFPFC is superior to that of non-AFPFC (NAFPFC) for pH process without disturbances, the overshoot of the effluent pH value of AFPFC with disturbances is decreased by 50% compared with that of NAFPFC; when the process parameters of AFPFC vary with time the integrated absolute error (IAE) performance index still retains to be less than 200 compared with that of NAFPFC.
Key words: Takagi-Sugeno (T-S) model; adaptive fuzzy predictive functional control (AFPFC); weighted recursive least square (WRLS); pH process
1 Introduction
Model predictive control (MPC), also referring to receding horizon control, deserves much research attention due to its design features of prediction and minimization of cost penalizing future deviations from an output reference trajectory. Many predictive control algorithms have also been presented in recent years [1], such as model algorithm control (MAC), dynamic matrix control (DMC), generalized predictive control (GPC) and predictive functional control (PFC). In these algorithms due to little computational burden and rapid control PFC has been widely applied in many engineering fields including industrial robots, chemical processes and radar tracking[2-3]. However, most controlled processes are inherently nonlinear in nature so that linear model cannot fit and predict the dynamic characteristics of nonlinear processes. Consequently, linear model predictive functional control (LPFC) may not always obtain satisfactory control results. Under such conditions, nonlinear model predictive functional control (NPFC) should be considered [4-5]. A strategy based on least squares support vector machine (LS-SVM) of nonlinear predictive functional control of recursive subspace model, was developed [6]. The prediction model of NPFC was Hammerstein model. Output function of nonlinear static link according to principle of LS-SVM was got, and linear dynamic link with model of recursive subspace was identified. ZHANG et al [7] used pseudo-partial derivative (PPD) to dynamically linearize a nonlinear system, and aggregation was applied to the predicted PPD, resulting in a model-free adaptive predictive control method for a nonlinear system. This method does not need nonlinear optimization, but only fits for weak nonlinear system.
T-S fuzzy models presented by Takagi and Sugeno, have got wide applications in system modeling and control since they can excellently express the dynamic characteristics of the complex nonlinear systems. Fuzzy predictive functional control (FPFC) based on T-S models has also become an attractive strategy in complex system control [8-10]. In Ref.[11] T-S models were used as the prediction model, and a single-variable fuzzy predictive functional control method was proposed and applied to a magnetic suspension system. Furthermore according to Ref.[11] a multi-variable fuzzy predictive functional control method was also given [12], and its stability was analyzed by using linear matrix inequality (LMI) [13]. But the above method can be used only under the condition that the number of the system input is equal to the system output, and that the influence of the model mismatch on the control performance of the system is not considered.
In this work, an adaptive fuzzy predictive functional control (AFPFC) method based on T-S models for multivariable nonlinear systems was proposed. Firstly, the antecedent parameters of T-S models were kept; the consequent parameters were identified by the weighted recursive least square (WRLS) method to compensate for the influence of model mismatch on the control performance. Secondly, T-S models were linearized to be state space model with time-varying parameters in each sampling instant; assuming that the basic function was step function the analysis solution of predictive control law was derived. Finally, the results for pH process were compared to show the effectiveness of the proposed AFPFC method.
T-S fuzzy model descriptions for multivariable nonlinear system
Consider a class of nonlinear systems which are approximated by a collection of coupled discrete-time fuzzy models of the input-output NARX (nonlinear autoregressive model with exogenous input) type
 l=1, 2, …, n (1)
l=1, 2, …, n (1)
where input vector  contains the current inputs, regression vector
contains the current inputs, regression vector 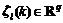 includes the current and lagged outputs and inputs
includes the current and lagged outputs and inputs
 (2a)
(2a)
 (2b)
(2b)
with
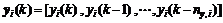
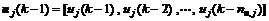
 ;
; 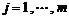
where ny, i and nu, j denote the orders of the ith output and the jth input, respectively; Rli denotes rule-based fuzzy models of T-S type [14]
Rli: IF  is
is  ,
, ,
, is Zli,q, u1(k) is Zli, q+1,
is Zli,q, u1(k) is Zli, q+1,  , um(k) is Zli, q+m, THEN
, um(k) is Zli, q+m, THEN
 (3)
(3)
i=1, 2, …, Kl; l=1, 2, …, n
where Zli is the antecedent fuzzy set of the lth output and the ith rule,  and
and  are the vectors containing the consequent parameters,
are the vectors containing the consequent parameters,  is the offset term, q=
is the offset term, q=
 is the number of antecedent variables,
is the number of antecedent variables,
and Kl is the number of fuzzy rules of the lth output. The model output is computed as the weighted average of the linear consequents in the individual rules
 (4)
(4)
with
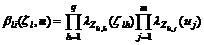
where  denotes the membership degrees of the antecedent variables, and
denotes the membership degrees of the antecedent variables, and  denotes fuzzy operator.
denotes fuzzy operator.
Let
 (5)
(5)
with
 , 0≤ωli(ζl, u)<1 (6)
, 0≤ωli(ζl, u)<1 (6)
Substituting Eq.(5) into Eq.(4), then the lth output of the fuzzy models can be expressed as
 (7)
(7)
3 On-line identification of T-S fuzzy models
There are many uncertainties and immeasurable disturbances in many industrial processes. Generally, model structure of most industrial processes sometimes does not change, therefore, the antecedent parameters of T-S models are kept, the WRLS method is used to on-line update the consequent parameters of T-S models for compensating for the influence of model mismatch on the control performance.
To identify the consequent parameters of T-S models, set

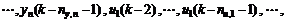
 (8)
(8)
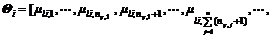
 (9)
(9)
Let
 ,
,
 ,
,
then Eq.(7) can be rewritten as
 (10)
(10)
where  is the regression vector,
is the regression vector,  is the unknown consequent parameter vector. The parameter vector
is the unknown consequent parameter vector. The parameter vector  can be identified by the following WRLS method:
can be identified by the following WRLS method:

 (11a)
(11a)
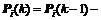
 (11b)
(11b)
where is the output prediction error, matrices
is the output prediction error, matrices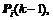
 result from the following partition of the covariance matrix
result from the following partition of the covariance matrix  ,
, is a nonnegative sequence of weighted coefficients.
is a nonnegative sequence of weighted coefficients.
The initial values of the identification algorithm are as follow:
 ,
, 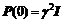
where  is very big positive real number, in general,
is very big positive real number, in general,  may be set to 1×104, I is an identity matrix, and ε is a very small positive real vector.
may be set to 1×104, I is an identity matrix, and ε is a very small positive real vector.
4 Adaptive fuzzy predictive functional control based on T-S models
AFPFC is still a model predictive control strategy with the basic traits including prediction model, receding optimization, and feedback correction.
4.1 Model prediction
To obtain the prediction model of the process, Eq.(7) is re-expressed as
 ,
,  (12)
(12)
with
 (13a)
(13a)
 (13b)
(13b)
 (13c)
(13c)
Define
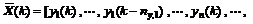

 ,
,
then T-S fuzzy models for MIMO (multiple-input multiple-output) nonlinear systems (7) are transformed into the linear time-varying state space model
 (14a)
(14a)
 (14b)
(14b)
where  , A(k) is the state matrix, B(k) is the control matrix, C(k) is the output matrix, and
, A(k) is the state matrix, B(k) is the control matrix, C(k) is the output matrix, and  is the offset vector. For simplification, here briefly note A, B, C, φ, and with
is the offset vector. For simplification, here briefly note A, B, C, φ, and with



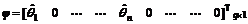
The state space model (14) is used to predict the process output. Let denote the h-step ahead state output at time k. In the whole predictive horizon the single-step linearization strategy is used to obtain the h-step ahead model output at time k according to Eq.(14):
denote the h-step ahead state output at time k. In the whole predictive horizon the single-step linearization strategy is used to obtain the h-step ahead model output at time k according to Eq.(14):
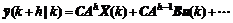
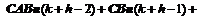
 (15)
(15)
4.2 Receding optimization
MPC is a control strategy based on the explicit use of a dynamic model of the process to predict the future behaviors of the process output over a certain horizon and to evaluate control actions to minimize a certain cost function. In general the predictive control law can be solved by minimizing the following cost function:
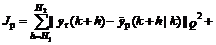
 (16)
(16)
where Q>0, R>0,  is the h-step ahead process output at time k,
is the h-step ahead process output at time k,  is the reference trajectory prediction value, H1 and H2 are the upper and lower limits of the prediction horizon respectively, and Hu is the control horizon.
is the reference trajectory prediction value, H1 and H2 are the upper and lower limits of the prediction horizon respectively, and Hu is the control horizon.
The reference trajectory yr may use the following form:
 (17)
(17)
with
 ,
,  ,
,
 ,
,
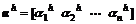
where  ,
,  is the reference trajectory value of the ith output at time k+h; ci(k+h) is the desired process output; yp, i(k) is the ith process measuring output at time k;
is the reference trajectory value of the ith output at time k+h; ci(k+h) is the desired process output; yp, i(k) is the ith process measuring output at time k;  exp(-ts/tr,i), ts is the sampling instant and tr, i is the reference trajectory response time of the ith output.
exp(-ts/tr,i), ts is the sampling instant and tr, i is the reference trajectory response time of the ith output.
4.3 Feedback correction
In practice, there are certain errors between the model output and the process measuring output due to the influence of model mismatch, noise, and unknown disturbance, thus error correction is necessary. Here, the prediction error e(k+h) can be approximately calculated by the following formulation:
 ,
,  (18)
(18)
where yp(k) and  are the process output and the model output at time k, respectively, and H is the prediction horizon. The corrected closed-loop h-step ahead output can be expressed as
are the process output and the model output at time k, respectively, and H is the prediction horizon. The corrected closed-loop h-step ahead output can be expressed as
 (19)
(19)
4.4 Solving predictive control law
According to the principle of PFC, the control signal is linear combination of some basic functions. For simplification, here the order of the basic function is only chosen as one, i.e., step function, and then we can know
 ,
,  (20)
(20)
Substituting Eq.(20) into Eq.(15), the model h-step ahead output is written as
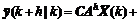
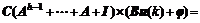
 (21)
(21)
According to the idea of the single-value MPC [12], substituting Eq.(21) into Eq.(16), the cost function (16) is simplified into
 (22)
(22)
Substituting Eqs.(17)-(19) into Eq.(22), the cost function (22) is minimized, and the optimal control law at time k is then obtained
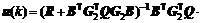
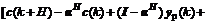
 (23)
(23)
where
 ,
, 
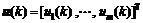
The obtained optimal control law u(k) at time k is applied to the process. At the next sampling instant the optimization problem is solved again with new measuring output from the process.
5 Application to pH process
In this section, a pH neutralization process is used to show the effectiveness of the proposed AFPFC method based on T-S models. The pH process is described by the following three nonlinear ordinary differential equations and one nonlinear equation [15]:
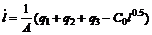
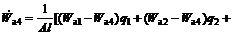
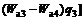
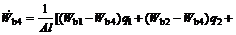
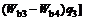
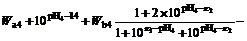
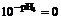
where q1, q2 and q3 are the flow rates of the acid, buffer, base, respectively; Wa1, Wa2, Wa3 and Wa4 are the reaction equilibrium constants of the acid, buffer, base, effluent, respectively; Wb1, Wb2, Wb3 and Wb4 are the material equilibrium constants, respectively; pH4 is the measuring value of the effluent pH; l is the liquid level; and the parameters and
and are the first and second disassociation constants of the acid. The nominal parameters and operating conditions [15] for pH process are listed in Table 1.
are the first and second disassociation constants of the acid. The nominal parameters and operating conditions [15] for pH process are listed in Table 1.
Table 1 Nominal operation parameters for pH process

The open-loop responses of the effluent pH for the acid and base flow rate change are shown in Fig.1. From the figures we can evidently see that pH process takes on strong nonlinearity, especially pH value lies in the operating regions from 3.5 to 5.5 and from 7 to 9.

Fig.1 Open-loop response of effluent pH: (a) Acid flow rate q1 change; (b) Base flow rate q3 change
Assuming that the buffer flow rate q2 and the effluent flow rate are kept constant, the effluent pH value is controlled by regulating the acid flow rate q1 and base flow rate q3. Firstly, a set of the input-output data for identifying T-S models of pH process are produced by exciting pH process using the random signal with different amplitudes and frequencies. G-K fuzzy clustering algorithm [9] and the WRLS method are applied to identifying the model antecedent parameters and consequent parameters respectively. The identified T-S model for pH process is described as follows:
R1: IF q3(k) is Z11, q1(k) is Z12, pH(k) is Z13, THEN
pH(k+1)=0.015q3(k)-0.102q1(k)+1.087pH(k)-0.011
R2: IF q3(k) is Z21, q1(k) is Z22, pH(k) is Z23, THEN
pH(k+1)=-0.05q3(k)+0.044q1(k)+1.064pH(k)+0.01
R3: IF q3(k) is Z31, q1(k) is Z32, pH(k) is Z33, THEN
pH(k+1)=-0.036q3(k)+0.072q1(k)+0.959pH(k)+0.017
R4: IF q3(k) is Z41, q1(k) is Z42, pH(k) is Z43, THEN
pH(k+1)=-0.049q3(k)+0.11q1(k)+0.955pH(k)+0.02
where Zi1, Zi2 and Zi3 (i=1, …, 4) are the membership functions of the base, acid, effluent pH, and shown in Fig.2.
Secondly, in order to show the validity of the identified T-S models for pH process a set of random bounded input verifying data are produced, and the input data are used to excite the identified T-S models and pH process. The comparison results of the process output and the model output are shown in Fig.3. We can see that the identified models are quite accurate; the absolute error between the obtained T-S model output and the process output is smaller than 0.015, which shows that the obtained T-S models can adequately reveal the dynamic characteristics of pH process.
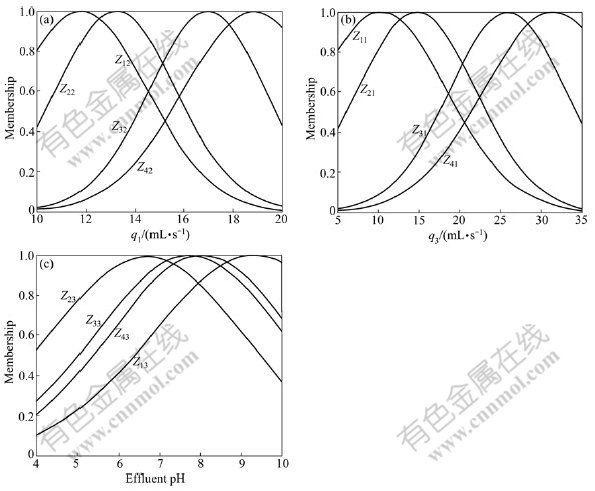
Fig.2 Fuzzy set partitions: (a) Acid flow rate q1; (b) Base flow rate q3; (c) Effluent pH

Fig.3 Validation of T-S fuzzy models: (a) Relationship between q1 and t; (b) Relationship between q3 and t; (c) Comparison of process output and model output; (d) Absolute error between model output and process output
Finally, to further demonstrate the effectiveness of the proposed AFPFC method, the control results of AFPFC are compared with those of NAFPFC for pH process. In simulation, the antecedent parameters of the identified T-S models are kept constant, the prediction model parameters for NAFPFC method are equal to the initial consequent parameters of the identified T-S models, and the prediction model are parameters for AFPFC method are on-line updated by the WRLS method. The prediction horizon H=10, the reference trajectory response time tr=20 s, the sampling instant ts=
1 s, Q=2, R= . Assuming that the disturbance of
. Assuming that the disturbance of
pH process output is the change of the buffer flow rate q2, the comparison results are shown in Figs.4-7. Fig.4 shows the comparison results via the proposed AFPFC method and NAFPFC method for the pH process with no disturbance. We can see that in the low operating region (pH<7) the AFPFC and NAFPFC methods may provide excellent set-value tracking performance, while in the relatively high operating region (pH>8) NAFPFC method provides poor set-value tracking due to the fact that the differences in actual pH process dynamics and the identified T-S models may lead to modeling errors. However, AFPFC method can still provide superior tracking performance. Fig.5 shows the comparison results via AFPFC and NAFPFC for pH process with disturbance q2. Due to the fact that the parameters of the identified T-S models are on-line updated and trained by using the WRLS method, the proposed AFPFC method can effectively overcome the influence of the disturbance. While using NAFPFC method the overshoot of the process effluent pH value is obviously greater than that of AFPFC. For example, when the buffer flow rate q2 step changes from 0.55 to 0.40 mL/s or from 0.40 to 0.30 mL/s the overshoot of the effluent pH value is decreased by 50% via AFPFC as compared with NAFPFC. Fig.6 shows the comparison results via AFPFC and NAFPFC for pH process with the time-varying parameters. When t>200 s, the parameters of pH process begin to vary with time, i.e. 6.35 at t= 200 s is linearly changed to 4.75 at t=400 s for the first disassociation constant of the acid  ; 10.25 at t=200 s is linearly changed to 8.65 at t=400 s for the second disassociation constant of the acid
; 10.25 at t=200 s is linearly changed to 8.65 at t=400 s for the second disassociation constant of the acid  . It can be clearly seen that NAFPFC method begins to become unsteady at t>200 s because of the influence of model mismatch between the obtained T-S models and the actual pH process, while the proposed AFPFC method can still steady the output response to the desired operating point by on-line identifying the consequent parameters of T-S models. The integrated absolute error (IAE) performance index comparison results are showed in Fig.7. It can be seen that the IAE performance index via AFPFC still retains below 200 at t=400 s as compared with that of NAFPFC even if the parameters of pH process vary with time.
. It can be clearly seen that NAFPFC method begins to become unsteady at t>200 s because of the influence of model mismatch between the obtained T-S models and the actual pH process, while the proposed AFPFC method can still steady the output response to the desired operating point by on-line identifying the consequent parameters of T-S models. The integrated absolute error (IAE) performance index comparison results are showed in Fig.7. It can be seen that the IAE performance index via AFPFC still retains below 200 at t=400 s as compared with that of NAFPFC even if the parameters of pH process vary with time.

Fig.4 Results of AFPFC and NAFPFC without disturbance: (a) Output response of pH process; (b) Controller output via NAFPFC; (c) Controller output via AFPFC

Fig.5 Results of AFPFC and NAFPFC with disturbance q2: (a) Output response of pH process; (b) Controller output via NAFPFC; (c) Controller output via AFPFC; (d) Flow rate of disturbance q2

Fig.6 Comparison results of AFPFC and NAFPFC with time-varying parameters: (a) Control result via NAFPFC; (b) Control result via AFPFC
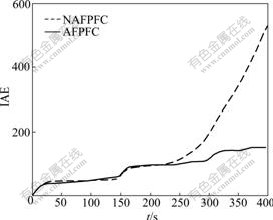
Fig.7 Performance index comparison between AFPFC and NAFPFC (IAE denotes integrated absolute error)
From these results above, we can conclude the proposed AFPFC method is a control scheme involving the excellent tracking and disturbance rejection ability. The superior control performance can be obtained through AFPFC over NFAPFC.
6 Conclusions
(1) Based on T-S fuzzy models multivariable nonlinear systems are described. Application of pH process shows the obtained T-S models have quite high modeling accuracy, and can adequately reveal the dynamic characteristics of complex processes.
(2) By using the WRLS method the consequent parameters of T-S models are on-line identified. AFPFC method can effectively compensate for the process parameters varying with time and disturbance, and make the controlled process possess good tracking performance and strong disturbance rejection.
(3) At each sampling instant, by dynamic linearization strategy the obtained T-S models are transformed into linear state space model with time-varying parameters. Linear predictive control technique is used to solve optimal predictive control law. Consequently, nonlinear optimization is avoided; the computational complexity and burden for AFPFC are decreased.
References
[1] QIN S J, BEDGWELL T A. A survey of industrial model predictive control technology [J]. Control Engineering Practice, 2003, 11(7): 733-764.
[2] YANG Xi-yun, XU Ling-feng, LIU Yi-bing, XU Da-ping. Multivariable predictive functional control for doubly fed induction generator [C]// IEEE International Conference on Control and Automation. New York: IEEE Press, 2007, 1: 80-83.
[3] BOUHENCHIRH, CABASSUDM, LELANNM V. Predictive functional control for the temperature control of a chemical batch reactor [J]. Computers and Chemical Engineering, 2006, 30(6): 1141-1154.
[4] ZHANG Quan-ling, WANG Shu-qing. Nonlinear predictive functional control using Hammerstein models [J]. Journal of Zhejiang University: Engineering Science, 2002, 36(2): 119-122. (in Chinese)
[5] ZHOU Hong-yu, ZHANG Jian, YOU Li-ke, ZHANG Feng. Nonlinear predictive function control based on hybrid neural network [J]. Control Theory and Applications, 2005, 22(1): 94-98. (in Chinese)
[6] ZHAO Hua-qi, CAO Jun, LI Zhi-wei, LIU Ya-qiu.Nonlinear predictive functional control of recursive subspace model using support vector machine [C]// Proceedings of the Chinese Control and Decision Conference. Shenyang: Northeastern University Press, 2008: 4909-4913.
[7] ZHANG Bin, ZHANG Wei-dong. Adaptive predictive functional control of a class of nonlinear systems [J]. ISA Transactions, 2006, 45(2): 175-183.
[8] LU Hong-li, JIA Lei, KONG Shu-lan, ZHANG Zhao-sheng. Predictive functional control based on fuzzy T-S model for HVAC systems temperature control [J]. Control Theory and Applications, 2007, 24(1): 94-98. (in Chinese)
[9] XING Zong-yi, HU Wei-li, JIA Li-min. Fuzzy predictive control based on T-S model [J]. Control and Decision, 2005, 20(5): 495-499. ( in Chinese)
[10] NUNEZ A, SAEZ D, OBLAK S, ?KRJANC I. Fuzzy-model-based hybrid predictive control [J]. ISA Transactions, 2009, 48(1): 24-31.
[11] LEPETIC M, ?KRJANC I, CHIACCIARINI H G, MATKO D. Predictive functional control based on fuzzy model: Magnetic suspension system case study [J]. Engineering Applications of Artificial Intelligence, 2003, 16(5/6): 425-430.
[12] OBLAK S, ?KRJANC L. Multivariable fuzzy predictive control of a MIMO nonlinear system [C]// Proceedings of the IEEE International Symposium on Intelligent Control, Limassol, Cyprus: IEEE Computer Society Press, 2005: 1029-1034.
[13] ?KRJANC I, BLAZIC S. Predictive functional control based on fuzzy model: Design and stability study [J]. Journal of Intelligent and Robotic Systems, 2005, 43(2/4): 283-299.
[14] MOLLOV S, BABU?KA R, ABONYI J, VERBRUGGEN H B. Effective optimization for fuzzy model predictive control [J]. IEEE Transactions on Fuzzy Systems, 2004, 12(5): 662-675.
[15] HALL R C, SEBORG D E. Modelling and self-tuning control of a multivariable pH process, part 1: modelling and multiloop control [C]// Proceedings of the American Control Conference. Pittsburgh, 1989: 1822-1827.
Foundation item: Project(2007AA04Z162) supported by the National High-Tech Research and Development Program of China; Projects(2006T089, 2009T062) supported by the University Innovation Team in the Educational Department of Liaoning Province, China
Received date: 2009-04-26; Accepted date: 2009-08-11
Corresponding author: SU Cheng-li, PhD, Associate professor; Tel: +86-413-6860167; E-mail: sclwind@sina.com
(Edited by LIU Hua-sen)