DOI: 10.11817/j.issn.1672-7207.2017.03.016

螺旋钻采煤机犁煤板的结构及参数分析

付林，杜长龙，李建平，杨道龙

(中国矿业大学 机电工程学院，江苏 徐州，221116)

摘要：为了提高螺旋钻采煤机犁煤板的收煤率，降低其能耗，提出3种结构形式的犁煤板，建立犁煤板物料回收离散元模型，利用该模型分别对不同形式犁煤板的结构参数进行仿真分析。研究结果表明：螺旋形犁煤板的收料比能耗和收煤率均随螺旋导程的增大而减小；圆弧形犁煤板的收煤率大体上随倾斜角的增大而减小，随圆弧半径的增大而增大；其收料比能耗大体上随倾斜角的增大先减小而后增大，随圆弧半径的变化无显著规律性；当倾斜角为40°左右，圆弧半径为300 mm左右时，犁煤板的收料比能耗较小；平面形犁煤板的收煤率大体上随铲角和倾角的增大而减小；收料比能耗大体上随铲角的增大而增大，随倾角的增大而减小；在研究的结构参数范围内，当铲角和倾角同时在30°左右取值时，犁煤板的比能耗较小；在3种结构形式的犁煤板中，倾角和铲角均为0°的平面形犁煤板能获得的收煤率最高。

关键词：螺旋钻采煤机；犁煤板；离散元模型；收煤率；收料比能耗；结构参数

中图分类号：TH122；TD421         文献标志码：A         文章编号：1672-7207(2017)03-0675-09

Structure and parameter analysis of auger miner’s coal plough

FU Lin, DU Changlong, LI Jianping, YANG Daolong

(School of Mechanical and Electrical Engineering, China University of Mining and Technology, Xuzhou 221116, China)

Abstract: In order to improve the coal recovery ratio and reduce energy consumption, three types of coal ploughs were presented and their structure parameters were studied respectively using the discrete element method (DEM). The results show that the recovery specific energy and coal recovery ratio of the spiral coal plough decrease with the increase of screw lead. For the circular coal plough, its coal recovery ratio decreases generally with the increase of tilt angle and the decrease of the arc radius, and its recovery specific energy decreases firstly and then increases with the increase of the tilt angle. The smaller recovery specific energy of the circular coal plough can be achieved when the tilt angle is chosen at around 40° and the arc radius is around 300 mm. For the plane coal plough, its coal recovery ratio decreases generally with the increase of pushing angle and tilt angle, and its recovery specific energy increases generally with the increase of pushing angle and the decrease of tilt angle. Within the scope of the selected parameters, the minimum specific energy of the plane coal plough can be achieved when the pushing angle and tilt angle are chosen at around 30° at the same time. In the three coal ploughs, the plane coal plough with 0° pushing angle and 0° tilt angle has the highest coal recovery ratio.

Key words: auger miner; coal plough; the discrete element method (DEM); coal recovery ratio; recovery specific energy; structure parameters

螺旋钻采煤机是一种适用于薄与极薄煤层开采的钻削式采煤设备，其基本组成及工作原理^[1]如图1所示。主机布置于煤岩巷道中，通过2排螺旋钻杆带动钻具最前端的多个钻头钻削采煤，钻头截割下的煤岩物料则由螺旋钻杆输送至巷道中的刮板输送机上。犁煤板是采煤机钻具上的浮煤清理装置，其基本作用是将堆积于风筒周围而无法被螺旋钻杆输送到的浮煤推移至两侧的钻杆作用区域，以此减少钻采过程中的丢煤率。犁煤板通常成组布置于稳定器处风筒的下方，其布置形式如图2所示。每个稳定器风筒下方均布置2组犁煤板：一组为前向犁煤板，另一组为后向犁煤板。每组前向或后向犁煤板又由2个沿风筒中心面对称布置的犁煤板组成。通常，前向犁煤板主要负责钻具钻进过程中的浮煤清理，而后向犁煤板则主要负责钻具退钻过程中的浮煤清理。一般钻具上每间隔4节钻杆的距离便布置前向和后向2组犁煤板。

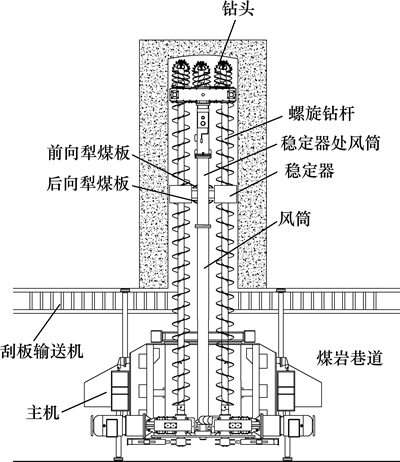
图1  螺旋钻采煤机采煤示意图

Fig. 1  Sketch of auger miner mining

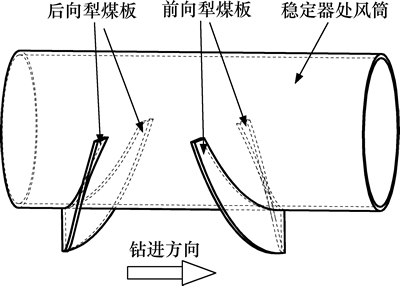
图2  犁煤板在风筒上的布置形式

Fig. 2  Arrangement for coal ploughs on ventilation pipe

作为螺旋钻采煤机上的浮煤清理装置，犁煤板的性能会直接影响犁煤板对浮煤的回收效率，同时也会影响回收过程中的能量消耗，因此，开展犁煤板的相关研究，提高其工作性能具有较好的经济价值。然而，目前对螺旋钻采煤机的研究主要集中于钻头截割及动态特性^[2-6]、钻具输送性能^[7-9]及钻具振动特性^[10-13]等方面，对犁煤板的相关研究很少。由于缺乏理论及实验指导，当前犁煤板主要采用经验法进行设计，其结构形式单一，几何参数的选取也具有一定的主观性。为此，本文作者拟采用离散单元法对犁煤板的物料回收过程进行数值模拟，在此基础上研究不同犁煤板结构形式及各结构形式下几何参数对犁煤板物料回收性能的影响规律，以期为犁煤板的结构设计和性能优化提供参考。

1  犁煤板物料回收离散单元模型

1.1  离散单元法基本理论

离散单元法是一种以牛顿第二定律为基础，通过跟踪每个颗粒的运动、颗粒间的接触及颗粒与外部边界的接触来模拟颗粒流动行为的数值仿真方法^[14-15]。在离散单元法中，颗粒间允许一定程度的相互重叠，颗粒间的重叠量和相对速度共同决定了颗粒间的相互作用力^[16-17]。本文采用线性弹簧-阻尼模型作为颗粒间的接触模型，颗粒间法向接触力F_n可表示为

              (1)

式中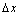：为颗粒间法向重叠量；k_n为颗粒间法向弹簧刚度；C_n为颗粒间法向阻尼器阻尼系数；v_n为颗粒间法向相对速度。

式(1)表明颗粒间的法向力由刚度系数为k_n的法向弹簧和阻尼系数为C_n的阻尼器描述。法向弹簧用于模拟颗粒间的排斥力，阻尼器用于消耗颗粒间动能。法向弹簧刚度系数k_n决定了颗粒间最大重叠量，通常颗粒间重叠量应为0.1%~0.5%，相应弹簧刚度数量级为10⁴~10⁶ N/m^[18]。阻尼系数的选取应取决于颗粒间的恢复系数，其与恢复系数间的关系见文献[19]。

颗粒间的切向作用力可表示为

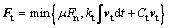        (2)

式中：μ为颗粒间静摩擦因数；k_t为颗粒间切向弹簧刚度；C_t为颗粒间切向阻尼器阻尼系数；v_t为颗粒间切向相对速度。

由式(2)可看出颗粒间切向相对速度积分得到切向作用力，其作用相当于1个渐进式弹簧，该弹簧存储了颗粒切向相对运动产生的能量，描述了颗粒切向的弹性变形。阻尼器用于吸收切向相对运动产生的能量，用于描述切向的塑性变形。总切向力受库仑摩擦力限制，即当切向力达到库仑摩擦力后，颗粒间便会产生相对滑动。

1.2  模型的假设与简化

实际工况下犁煤板的物料回收模型如图3(a)所示。犁煤板沿风筒轴线方向(Z向)推动堆积于风筒周围的浮煤，让其由中间煤孔区域往两侧煤孔区域运动，使其到达钻杆作用范围后被输送至巷道。事实上，犁煤板的物料回收过程十分复杂。物料不仅会在犁煤板作用下由风筒区域向两侧煤孔区域运动，而且会在钻杆作用下由两侧煤孔区域往风筒区域运动，即物料的回收过程是一个双向流动过程(见图3(a))。同时，由于犁煤板与风筒间的刚性连接，钻具的变形和随机振动使得犁煤板的运动规律极为复杂，犁煤板不仅有沿风筒轴线的进给运动，而且有沿其他方向的随机振动。此外，煤孔形态的不规则性及煤岩物料的非线性均使犁煤板的物料回收过程更加复杂。鉴于此，为简化模型，同时结合本文研究需要，对犁煤板的物料回收过程进行如下假设：1) 物料仅在犁煤板作用下由风筒区域向两侧钻杆区域运动，而不会在钻杆作用下作反向运动；2) 犁煤板只会随钻具沿钻进方向作匀速直线运动，不会因钻具变形和振动出现其他形式的运动；3) 各煤孔内表面为理想的圆柱形表面，煤孔表面没有因钻采偏斜、钻具振动、煤岩崩落等原因而引起不规则变形；4) 堆积于风筒附近的浮煤物料均在重力作用下处于平衡状态；5) 犁煤板作用的煤岩物料为理想的非黏性散体干颗粒。

图3  犁煤板物料回收模型

Fig. 3  Models of coal plough recycling material

根据以上假设，可建立犁煤板物料回收简化模型，如图3(b)所示。风筒区域物料在重力作用下主要堆积于中间煤孔底部，故简化模型只建立中间煤孔的下半部分圆柱面。由于不考虑钻杆对浮煤物料的作用及物料的双向流动，简化模型省略钻杆实体。同时，为方便后续离散单元模型建立，用两长方体集料槽代替左右两侧的煤孔，以实现对回收物料的收集。

1.3  离散单元模型的建立

本文以离散元软件PFC3D作为仿真平台对犁煤板的物料回收过程进行数值模拟。根据图3中的简化模型，可建立犁煤板物料回收离散单元模型，如图4所示。该模型由几何实体、物料颗粒和边界条件几部分组成。几何实体是指所有可能与物料颗粒发生相互作用的几何结构，此处包括中间煤孔、犁煤板、风筒和集料槽。几何实体通常用不同形状的墙体模型进行描述。风筒和集料槽形状较简单，此处分别用圆柱形墙体和平面墙体进行构建。由于结构相对复杂，犁煤板和煤孔采用CAD软件进行实体建模，然后采用多个三角形墙体对其离散以近似描述其几何外形，二者的离散化墙体模型如图5所示。浮煤物料用球形颗粒进行描述。物料颗粒的产生方法为：在中间煤孔上方区域生成一定数量的球形颗粒，然后在重力状态下自由沉降以达到平衡状态，去除多余颗粒。本离散单元模型的边界条件主要是指犁煤板和风筒的推进速度，设定为20 mm/s。离散元模型的基本结构参数如下：煤孔总长为3 500 mm，物料堆积长度为2 800 mm，物料堆积高度为200 mm，煤孔半径为225 mm，风筒直径为219 mm。

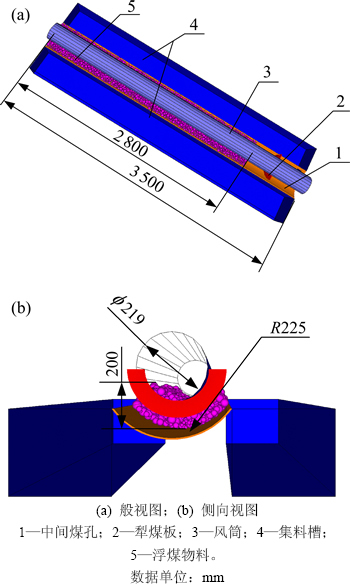
图4  犁煤板物料回收离散单元模型

Fig. 4  Discrete element models of coal plough recycling material

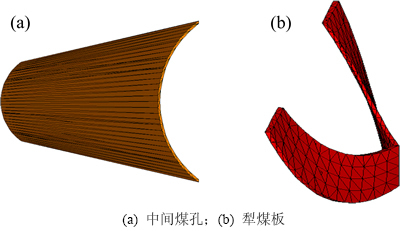
图5  三维实体的离散化墙体模型

Fig. 5  Discrete wall models of three-dimensional entity

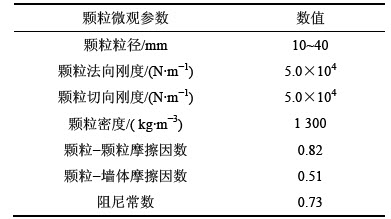
离散单元法通过对颗粒及墙体微观参数的定义以间接描述散体物料的宏观力学行为。浮煤物料颗粒的微观参数见表1。为了避免颗粒对墙体的穿透，墙体刚度通常比颗粒刚度大1~2个数量级，所有墙体法向和切向刚度均为7.0×10⁵ N/m。

利用图4中的离散单元模型，通过改变模型中犁煤板的结构形式或几何参数可实现对不同犁煤板的物料回收性能研究。对于犁煤板，收煤率和收料比能耗是最重要的2种物料回收性能评价指标。收煤率是指犁煤板作用一定长度范围的物料后，其回收到的物料质量占回收前该长度范围内待回收物料总质量的百分比。收料比能耗是指犁煤板回收单位质量的浮煤物料所消耗的能量。

表1  物料颗粒微观参数

Table 1  Micro-parameters of material particles

犁煤板的物料回收过程模拟如图6所示。当犁煤板和风筒以一定速度作用待回收物料后，一部分物料在犁煤板作用下进入两侧的集料槽，成为被回收到的物料，另一部分物料则仍留在中间煤孔中，成为被丢弃的物料。通过对仿真过程犁煤板的功率值进行实时监测，可获取犁煤板任何时间段内的总能耗。同时，通过统计一定时间段内集料槽区域的颗粒质量，可以获取犁煤板的收煤率。

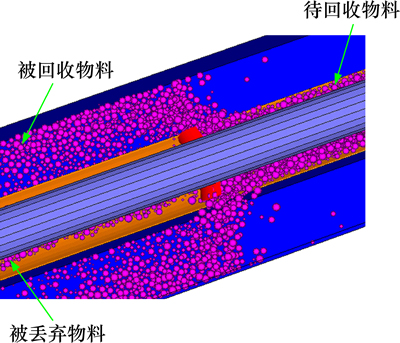
图6  犁煤板的物料回收模拟

Fig. 6  Simulation of coal plough recycling material

2  犁煤板的结构形式和参数

目前，螺旋钻采煤机犁煤板的结构形式较单一，主要为螺旋形犁煤板。为了探求更合理的犁煤板结构，提出圆弧形和平面形两种新的犁煤板结构形式。加上原有的螺旋形犁煤板，3种不同结构形式的犁煤板如图7所示。3种犁煤板间的主要差异是其工作表面形状不同，螺旋形犁煤板的工作表面形状为等导程空间螺旋面，圆弧形犁煤板的工作表面形状为空间圆柱面，而平面形犁煤板的工作表面形状则为空间平面。尽管3种犁煤板的几何形状存在差异，但其在风筒径向平面上的投影形状完全相同，如图8所示。图8中：R_f为犁煤板的内孔直径，即风筒外表面直径；R_s为犁煤板的外缘直径；α为犁煤板的围包角，即对称布置的两犁煤板绕风筒周向的夹角。一般地，犁煤板的外缘直径越大，越利于物料回收，但过大的外缘直径会降低钻具对煤层的适应性，故通常犁煤板外缘与煤孔间应保留50~60 mm间隙。犁煤板焊接在风筒上，故其内孔直径由风筒外表面直径决定。犁煤板的围包角越大，物料越不易越过犁煤板顶部进入其后方。然而，为了给风筒上其他构件预留空间，犁煤板的围包角通常要求不超过180°。在本文的研究中，R_f，R_s和α均保持为常数，分别取219 mm，339 mm和180°。

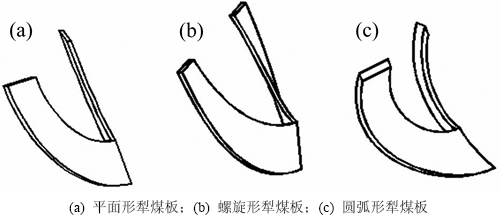
图7  不同结构形式的犁煤板

Fig. 7  Coal ploughs with different structures

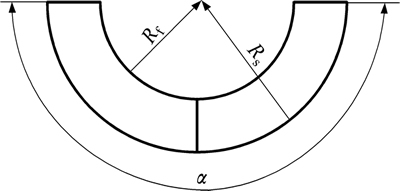
图8  犁煤板在风筒径向面的投影

Fig. 8  Projection of coal plough on radial plane of ventilation pipe

2.1  平面形犁煤板参数分析

对于平面形犁煤板，由于其工作表面为空间平面，因此，在外缘直径、内孔直径及围包角固定的前提下，通过定义工作表面的2个空间方位角度便可唯一确定犁煤板的几何外形。2个空间角度分别为倾角和铲角，其定义见图9。平面B为两犁煤板的对称面，平面A为过风筒轴线且与平面B相垂直的平面。坐标系Oxyz固定在风筒上，x轴平行于风筒轴线，正向与犁煤板推进方向一致，y轴位于平面A内且与x轴垂直，z轴由x和y轴根据右手法则确定。直线Op为犁煤板工作表面的外法线。倾角定义为平面形犁煤板工作表面与风筒径向平面所夹锐角，等同于图中角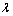。铲角定义为平面形犁煤板工作表面与平面A间所夹的锐角，等同于图9中角。

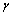为研究2个角度结构参数对平面形犁煤板物料回收性能的影响，将2个角度作为实验因素，每种因素取4个水平进行完全实验。此外，倾角和铲角均分别选取0°，20°，40°和60°，按照完全实验要求，共进行16次数值实验。各数值实验安排及实验统计结果见表2。

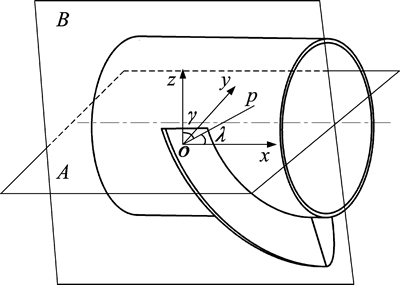
图9  平面形犁煤板的结构参数

Fig. 9  Structure parameters of plane coal plough

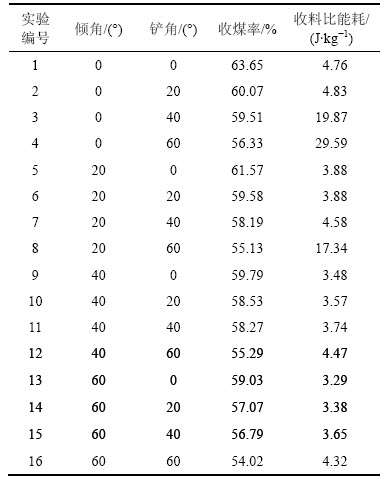
表2  平面形犁煤板的实验安排与结果统计

Table 2  Experimental arrangement and result statistics of plane coal plough

根据表2，采用插值算法，可得平面形犁煤板的2种物料回收性能指标与角度间的关系，见图10。从图10(a)可知：平面形犁煤板的收煤率随铲角和倾角的增大均大体呈逐渐减小的变化趋势；当铲角和倾角同时为0°即犁煤板工作平面与风筒轴线相垂直时，平面形犁煤板的收煤率最大。从图10(b)可知：除个别局部区域外，平面形犁煤板的收料比能耗大体随倾角的增大而逐渐减小，随铲角的增大而逐渐增大；当倾角过小且铲角过大时，平面形犁煤板的收料比能耗会急剧增大；在研究的参数范围内，当倾角和铲角均在30°左右取值时，平面形犁煤板的收料比能耗能达到较优值。对比图10(a)和图10(b)及对2种物料回收性能指标的变化规律可知：无论平面形犁煤板的铲角和倾角如何取值，均无法保证犁煤板在拥有最大收煤率的同时拥有最低的收料比能耗。换言之，对于平面形犁煤板，铲角和倾角是1对矛盾体，无法通过二者的合理匹配让这2种物料回收性能指标同时达到最优化。

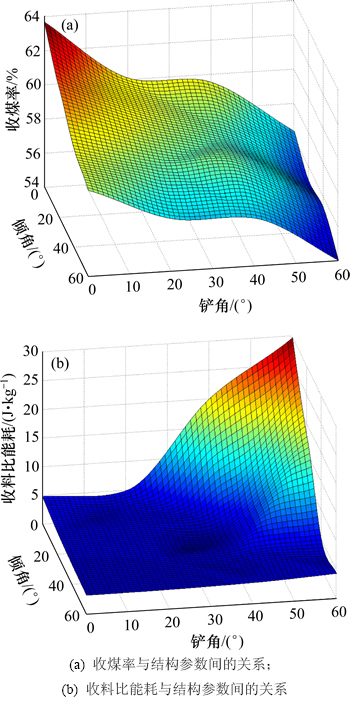
图10  平面形犁煤板回收性能指标与结构参数间的关系

Fig. 10  Relationship between recycling performance indicators of plane coal plough and structure parameters

2.2  螺旋形犁煤板的参数分析

对于螺旋形犁煤板，由于其工作表面为等导程空间螺旋面，因此，在螺旋面的外缘直径、内孔直径及围包角固定的前提下，螺旋导程可作为确定犁煤板几何外形的唯一参数。为了研究螺旋导程对螺旋形犁煤板物料回收性能的影响，此处选取52，202，352和502 mm这4种导程进行数值实验，实验结果见表3。

表3  螺旋形犁煤板的实验安排及结果统计

Table 3  Experimental arrangement and result statistics of spiral coal plough

根据表3可得螺旋形犁煤板两物料回收与螺旋导程间的关系，见图11。从图11(a)可知：螺旋形犁煤板的收煤率随螺旋导程的增大按线性函数统计规律逐渐减小。按该变化规律推测，当螺旋导程取极限值0 mm时，螺旋形犁煤板的收煤率取得最大值。事实上，螺旋导程为0 mm时螺旋形犁煤板的外形与倾角和铲角均为0°的平面形犁煤板相同，由表2可知此时犁煤板的收煤率为63.65%，该值均大于表3中各收煤率统计结果，由此说明推测的正确性。从图11(b)可知：螺旋形犁煤板的收料比能耗随螺旋导程的增大按指数函数统计规律逐渐减小；当螺旋导程取值大于400 mm时，其变化对犁煤板收料率的影响程度变小。据分析可知，随螺旋导程的增大，螺旋形犁煤板的2个回收性能指标变化具有矛盾性，即犁煤板收料比能耗减小的同时，其收煤率也会随之减小，二者无法同时达到最优化。由表3可知：当螺旋导程从52 mm增大至502 mm时，螺旋形犁煤板的收煤率仅减小6.96%，而其收料比能耗降低17.76%，故螺旋导程对犁煤板收料比能耗的影响较大。

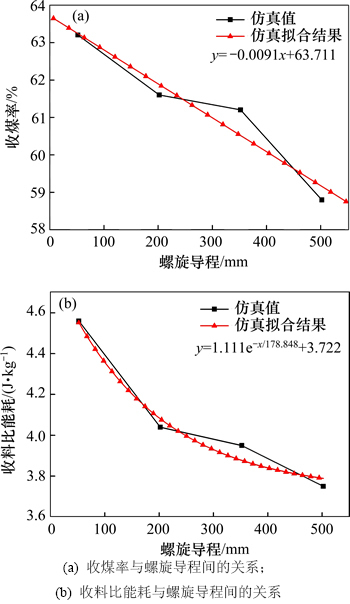
图11  螺旋形犁煤板回收性能指标与螺旋导程间的关系

Fig. 11  Relationship between recycling performance indicators of spiral coal plough and screw lead

2.3  圆弧形犁煤板参数分析

对于圆弧形犁煤板，其在风筒上的布置方式如图12所示。犁煤板的圆弧面中心线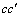始终与2块犁煤板的对称平面B垂直，且位于风筒轴线与犁煤板最下方点P间的中心位置。根据该布置方法，在外缘直径、内孔直径及围包角固定的前提下，圆弧形犁煤板的几何外形可由圆弧直径和倾斜角2个参数唯一确定。2种结构参数的定义如图12所示。其中，为固定在风筒上的空间直角坐标系，坐标轴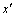与风筒轴线平行，正向为犁煤板推进方向。圆弧直径是指圆弧形犁煤板的圆弧形工作表面，直径为2R。倾斜角定义为圆弧面中心线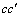与风筒径向平面间所夹的锐角，等同于图12中的角。

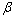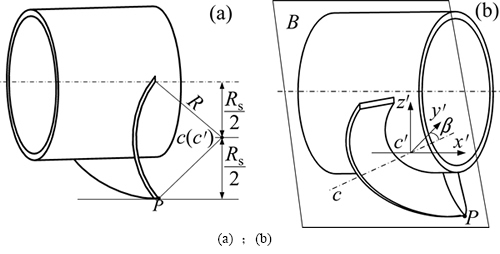
图12  圆弧形犁煤板的布置及结构参数

Fig. 12  Arrangement and structure parameters of circular coal plough

为了研究2种结构参数对犁煤板物料回收性能的影响，将2种参数作为2种实验因素，每种因素取4个水平进行完全实验。此外，圆弧直径取170，270，370和470 mm，倾斜角取0°，20°，40°和60°，按照完全实验要求共进行16次数值实验。各数值实验安排及实验统计结果见表4。

表4  圆弧形犁煤板的实验安排及结果统计

Table 4  Experimental arrangement and result statistics of circular coal plough

圆弧形犁煤板的收煤率与2个结构参数间的关系如图13所示。从图13(a)可知：圆弧形犁煤板的收煤率大体上随倾斜角的增大而逐渐减小，随圆弧半径的增大而逐渐增大。根据该变化规律推测，当圆弧形犁煤板的倾斜角为0°，圆弧半径为无限大时，其收煤率将会最大。事实上，该极限取值条件下的圆弧形犁煤板外形与倾角和铲角均为0°的平面形犁煤板外形完全相同，由表2可知，此时犁煤板的收煤率为63.65%，该值均大于表4中各收煤率统计结果，由此说明推测的正确性。由图(13(b)可知，圆弧形犁煤板的收料比能耗大体上随倾斜角的增大呈先减小后增大的变化趋势，随圆弧直径的变化无显著规律性。然而，由图13(b)可看出：在选取的参数范围内，当倾斜角在40°左右取值，圆弧半径在300 mm左右取值时，圆弧形犁煤板的比能耗将会最小。对比图13(a)和图13(b)可看出：不存在某个取值区域让圆弧形犁煤板的收煤率最大的同时，使其收料比能耗最低，即无法通过倾斜角和圆弧直径的合理匹配使圆弧形犁煤板的2种物料回收性能指标同时达到最优化。

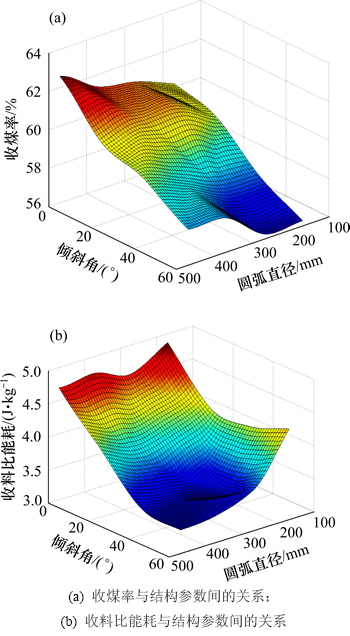
图13  圆弧形犁煤板回收性能指标与结构参数间的关系

Fig. 13  Relationship between recycling performance indicators of circular coal plough and structure parameters

3  犁煤板的结构和参数选取

犁煤板的收煤率越高，意味着钻采过程中丢失的煤岩物料越少，资源的回收率越高；犁煤板的收料比能耗越低，意味着在物料回收过程中消耗的能量越少，回收过程成本越低。然而，无论对于哪种结构形式的犁煤板，均无法通过其自身几何参数间的匹配使收煤率和收料比能耗同时达到最优化。因此，若按照现有的方式在钻具上布置结构形式和几何参数均完全一致的犁煤板，将无法获得较理想的物料回收效果。

犁煤板有前向和后向之分，前向犁煤板负责钻进过程的浮煤物料回收，而后向犁煤板负责退钻过程的浮煤回收。尽管前向与后向犁煤板的物料回收模型及工作原理完全相同，但由于作用过程的差异，使得钻具对2类犁煤板的物料回收性能要求有差异。对于前向犁煤板，只需在物料回收过程中保持较低的收料比能耗，而无需拥有最大的收煤率。因为前向犁煤板未充分回收的浮煤物料，可在退钻过程中由后向犁煤板再次进行回收。相反，对于后向犁煤板，则需拥有尽可能大的收煤率，而无需拥有最低的收料比能耗。因为后向犁煤板负责退钻过程的物料回收，若在该过程中物料未被犁煤板充分回收，则会被永久丢弃而造成严重的资源浪费。因此，进行犁煤板设计时，前向犁煤板应以收料比能耗最低作为设计原则，而后向犁煤板应以收煤率最高作为设计原则。

对于每种结构形式的犁煤板，通过合理的结构参数匹配均能获得较低的收料比能耗，因此，前向犁煤板可选取文中提出的任何一种结构形式。在所有结构形式的犁煤板中，铲角和倾角均为0°的平面形犁煤板拥有最优的收煤率，因此，该犁煤板可作为钻具上的后向犁煤板。

4  结论

1) 对于任何一种结构形式的犁煤板，其收煤率和收料比能耗2种物料回收性能指标均存在一定矛盾，即无法单纯通过犁煤板自身结构参数的匹配以使2个指标同时达到最优化。

2) 平面形犁煤板的收煤率大体上随铲角和倾斜角的增大而减小，收料比能耗大体上随铲角的增大而增大，随倾斜角的增大而减小。螺旋形犁煤板的收煤率和收料比能耗均随螺旋导程的增大而减小。圆弧形犁煤板的收煤率大体随倾斜角的增大而减小，随圆弧半径的增大而增大；比能耗大体随倾斜角的增大先减小后增大，随圆弧半径的变化无显著规律性。

3) 在所有结构形式的犁煤板中，倾角和铲角均为0°的平面形犁煤板收煤率最高。当倾斜角在40°附近取值，圆弧半径在300 mm左右取值时，圆弧形犁煤板的收料比能耗较小；当铲角和倾角均在30°左右取值时，平面形犁煤板的收料比能耗较小。

4) 在进行犁煤板设计时，前向犁煤板应以收料比能耗最低为设计原则，后向犁煤板应以收煤率最高为设计原则。

参考文献：

[1] STONIS M, HUDECEK V. Mining of coal pillars using the drilling method[J]. Acta Montanistica Slovaca, 2009, 14(3): 241-249.

[2] 林其岳. 螺旋钻采煤机钻具的参数研究及优化[D]. 阜新: 辽宁工程技术大学机械工程学院, 2009: 20-35.

LIN Qiyue. Drilling tools parameter research and optimization of coal auger[D]. Fuxin: Liaoning Technical University. School of Mechanical Engineering, 2009: 20-35.

[3] 朴京爱. 螺旋钻采煤机钻头的载荷谱分析[D]. 阜新: 辽宁工程技术大学机械工程学院, 2010: 5-42.

PU Jingai. Analysis of load spectrum on coal auger bits[D]. Fuxin: Liaoning Technical University. School of Mechanical Engineering, 2010: 5-12.

[4] 付林, 杜长龙, 刘送永, 等. 螺旋钻采煤机钻头截齿载荷特性研究[J]. 中国机械工程, 2013, 24(15): 2020-2024.

FU Lin, DU Changlong, LIU Songyong, et al. Research on load characteristics of picks on auger drill miner’s aiguille[J]. China Mechanical Engineering, 2013, 24(15): 2020-2024.

[5] FU Lin, DU Changlong, CUI Xinxia, et al. Simulation study on cutting performance of auger drill miner’s aiguille[J]. International Journal of Earth Sciences and Engineering, 2014, 7(1): 83-89.

[6] 毕耀坤. 螺旋钻采煤机钻头布齿及其截割过程动力学分析[D]. 重庆: 重庆大学机械工程学院, 2013: 37-70.

BI Yaokun. Teeth-arrangement and dynamic analysis of cutting process for coal auger-bit[D]. Chongqing: Chongqing University. College of Mechanical Engineering, 2013: 37-70.

[7] 李晓豁, 林其岳, 何洋. 基于GAAA算法的螺旋钻采煤机输送机构参数的优化[J]. 煤炭学报, 2010, 35(3): 498-502.

LI Xiaohuo, LIN Qiyue, HE Yang. Parameter optimization of spiral conveyor for coal auger based on GAAA algorithm[J]. Journal of China Coal Society, 2010, 35(3): 498-502.

[8] 李晓豁, 郭继文, 邓云, 等. 基于人工鱼群算法的螺旋钻采煤机二次破碎率最低的参数优化设计[J]. 煤炭学报, 2011, 36(2): 346-350.

LI Xiaohuo, GUO Jiwen, DENG Yun, et al. Parameter optimization of lowest secondary crushing rate for coal auger based on artificial fish school algorithm[J]. Journal of China Coal Society, 2011, 36(2): 346-350.

[9] 张强, 聂国强, 李守巨. 螺旋钻采煤机承压输送数学模型及仿真研究[J]. 煤炭学报, 2013, 38(1): 231-235.

ZHANG Qiang, NIE Guoqiang, LI Shouju. Study on mathematical model of confined transportation of coal auger and simulation[J]. Journal of China Coal Society, 2013, 38(1): 231-235.

[10] 李晓豁, 郭继文, 王丽, 等. 螺旋钻采煤机输送机构振动频率的计算与分析[J]. 广西大学学报, 2011, 36(6): 897-902.

LI Xiaohuo, GUO Jiwen, WANG Li, et al. Calculation and analysis of vibration frequency of spiral conveyor for coal auger[J]. Journal of Guangxi University, 2011, 36(6): 897-902.

[11] FU Lin, DU Changlong, GAO Kuidong. Dynamical simulation model of auger miner's working mechanism based on virtual prototyping technology[J]. Advanced Materials Research, 2011, 338: 199-204.

[12] LIU Songyong, CUI Xinxia, LIU Xiaohui. Coupling vibration analysis of auger drilling system[J]. Journal of Vibroengineering, 2013, 15(3): 1442-1453.

[13] CUI Xinxia, JI Huifu, LIN Minxing, et al. Vibration characteristic analysis of the multi drilling mechanism[J]. Journal of Vibroengineering, 2014, 16(6): 2722-2734.

[14] 温彤, 雷杰, 裴春雷. 一种离散单元法的弹性可变形颗粒模型[J]. 重庆大学学报, 2009, 32(7): 743-746.

WEN Tong, LEI Jie, PEI Chunlei. Elastic deformable particle model in discrete element method[J]. Journal of Chongqing University, 2009, 32(7): 743-746.

[15] 刘瑜. 井下冲撞式煤矸分离中颗粒动力学行为研究[D]. 徐州: 中国矿业大学机电工程学院, 2011: 91-92.

LIU Yu. Study on particle dynamics of impact separation for coal and gangue underground[D]. Xuzhou: China University of Mining and Technology. School of Mechanical and Electrical Engineering, 2011: 91-92.

[16] CLEARY P W. DEM simulation of industrial particle flows: case studies of dragline excavators, mixing in tumblers and centrifugal mills[J]. Powder Technology, 2000, 109(3): 83-104.

[17] CLEARY P W, SAWLEY M L. Three-dimensional modelling of industrial granular flows[C]// Second International Conference on CFD in the Minerals and Process Industries. Melbourne, Australia, 1999: 95-100.

[18] MCBRIDE W, CLEARY P W. An investigation and optimization of the ‘OLDS’ elevator using discrete element modeling[J]. Powder Technology, 2009, 193(3): 216-234.

[19] CLEARY P W. Predicting charge motion, power draw, segregation and wear in ball mills using discrete element methods[J]. Minerals Engineering, 1998, 11(11): 1061-1080.

(编辑  陈灿华)

收稿日期：2016-03-10；修回日期：2016-05-22

基金项目(Foundation item)：国家高技术研究发展计划(863计划)项目(2012AA062102)；国家自然科学基金资助项目(51375478) (Project (2012AA062102) supported by the National High Technology Research and Development Program(863 Program) of China;Project (51375478) supported by the National Natural Science Foundation of China)

通信作者：杜长龙，博士，教授，从事矿山机械设计研究；E-mail: cumtdcl@163.com