高速铁路过渡段路基自振频率的模态分析与试验

陈湘亮^{1, 2}，王永和¹，王灿辉²

(1. 中南大学 土木工程学院，湖南 长沙，410075；

2. 湖南城市学院 土木工程学院，湖南 益阳，413000)

摘要：通过建立有限元模型，对武广(武汉—广州)高速铁路过渡段路基进行模态分析，获得路基的竖向自振频率。同时，在路基中埋设传感器，获取环境激励路基振动时程曲线及列车过后的衰减自由振动波形，分别采用傅里叶变换原理及最大熵谱法对其进行自振频率分析。研究结果表明：模态分析与现场实测所获得的路基自振频率基本相近，可以采用模态分析来获得路基的自振频率；采用最大熵谱法对现场实测的路基衰减自由振动波形进行频谱分析更易于分析路基的固有频率，并且可以得到较准确的测试结果。

关键词：过渡段；路基；自振频率；模态；最大熵谱

中图分类号：U213.1         文献标志码：A         文章编号：1672-7207(2012)01-0322-06

Modal analysis and experiment research on natural frequencies of transition section subgrade of high-speed railway

CHEN Xiang-liang^{1, 2}, WANG Yong-he¹, WANG Can-hui²

(1. School of Civil Engineering, Central South University, Changsha 410075, China;

2. College of Civil Engineering, Hunan City University, Yiyang 413000, China)

Abstract: Based on the finite element model, the vertical natural frequency of subgrade was obtained through the modal analysis of the subgrade transition section of Wu-Guang (Wuhan—Guangzhou) High-speed Railway. The time history of vibration and damped free vibration waveform of the subgrade were acquired by ambient excitation and train loads excitation, and the nature frequency was obtained through principle of Fourier transform and maximum entropy spectrum method. The result of modal analysis was chosen in actual measurement. The results show that the model is correct and the natural frequency of the subgrade can be acquired through modal analysis. In the field measurement, the accurate test results are easy to be obtained through frequency spectrum analysis in the maximal entropy spectrum method of the damped free vibration waveform of the subgrade.

Key words: transition section; subgrade; natural frequency; modal; the maximum entropy spectrum

随着我国高速铁路运行速度的提高，列车对线路的激励强度将增大，激励频率也随之提高，路基的振动问题也成为研究的重要课题。当列车以一定速度通过路基时，将对路基产生激励荷载，使路基受迫振动；当激励频率与路基自振频率一致或相近时，将产生共振，使列车与轨道振动加剧导致振动加速度幅值急剧变大，而路基振动加速度是判断振动对轨道破坏作用的主要参数, 进而影响列车的行驶安全和乘客的舒适度^[1-3]。为了防止共振的发生，列车的激励频率应尽量避开路基的固有频率；因此，如何准确地测试路基的自振频率就显得十分重要。路基的振动加速度幅值与路基动力特性和荷载作用频率密切相关^[4-5]，而路基自振频率分析是动态响应分析的基础和出发点。许多震害是由于共振或类共振效应引起的，为了较准确地估计和防止这类灾害的发生，激励频率应尽量避开结构的固有频率。国内外不少学者从理论上研究了地基固有频率的特性及其计算方法。陈龙珠等^[6-7]提出采用机械阻抗法计算成层地基的固有频率，即采用常见的水平成层地基的剪切梁模型，导出地基表面位移阻抗与频率的关系式，其阻抗绝对值的最小值所对应的频率便为成层地基的固有频率。但该方法需采用跨孔法测定土中剪切波速度与深度的变化关系曲线。日本在修建东海道新干线时对路堤现场进行了共振试验，测得路基共振频率为15~20 Hz。杨学林等^[8]利用地脉动来测试并分析地基的自振周期。聂志红等^[4]在秦沈客运专线利用环境激励对路基自振频率进行了分析，但地脉动谱的峰值频率有多个，有的可能是脉动源的优势频率而非地基自振频率，而根据地脉动谱的峰值频率来识别地基自振频率存在一定的主观性^[8]。在此，本文作者对武广(武汉—广州)高速铁路涵-涵过渡段进行模态分析获得路基的自振频率；在试验段埋设测试原件，采用环境激励测试获得分析结果并与之比较，在现场实测时，提出对被激励结构的衰减自由振动波形更易于分析路基的固有频率。

1  工程概况

武广高速铁路全长为995 km，设计时速为350 km/h，线路长，标准高。沿线地形起伏大，加之交通、灌溉、排水等需要，设置于路基地段的涵洞密度较大。全线有520座桥梁、110座隧道、900座涵洞，路堤与路堑联结处达1 600多处。为了减小刚性构筑物与土质路基间的刚度差异以及不同构筑物间过大的差异沉降，需要在不同构筑物联结处设置过渡段，以使其刚度与变形均匀过渡，确保列车高速、安全、平稳和乘客舒适。以上提到的4类过渡段总计4 660处，分布在280 km的路基中，平均每60 m左右设置1处过   渡段。

DK1252+679～DK1252+731段为涵-涵间短路基过渡段试验区段，全长52 m，其纵断面见图1。垄岗低缓，自然坡度约10°，相对高差为10~20 m。地层岩性及地质构造如下：垄岗表层为Q4el+dl粉质黏土，硬塑，厚约0.5 m；下为Q2+3粉质黏土，硬塑，厚3~6 m；下伏J3泥质粉砂岩夹薄层粉砂岩、粉砂质泥岩，褐红色，全-弱风化。水文地质条件如下：垄岗地下水较发育，主要为孔隙潜水及毛细水，水位埋深2.0~5.0 m，接受大气降水补给。

该过渡段填高1.7 m，地基采用CFG桩加固，桩径0.5 m，按正三角形布置，桩顶均铺设0.6 m厚的碎石垫层，内铺一层极限抗拉强度不小于80 kN/m的土工格栅。基床表层0.4 m采用级配碎石(加5%水泥)填筑；路堤基床底层填筑A和B组填料，路基底部设4%的排水坡。

2  过渡段模态分析

2.1  理论分析

过渡段路基系统包括钢轨、扣件、轨下胶垫、轨道板、CA砂浆层、整体混凝土道床、级配碎石层(加5%水泥)、A和B填料层、地基CFG桩加固层及其下卧层等。采用有限元理论建立无砟轨道-路基-地基计算模型。假定过渡段轨下结构各层都由均质、各向同性的弹性材料组成，各结构层之间接触面完全连续。各结构层之间位移通过不同约束方程连为一体。根据圣维南原理，可将线路两端及地基层很深的底部均视为固定约束。对于不同结构层采用不同的单元去离散。其中钢轨采用Timoshenko梁单元，轨道板和CA砂浆层采用板单元，钢轨和轨道板之间的扣件和轨下胶垫结构系统采用弹簧-阻尼单元，地基层采用无限元以消除边界效应的影响，其他结构层采用三维实体单元。不同材料接触面之间相互耦合，无相对位移，其耦合约束方程采用Lagrange乘子法处理^[9-15]。

图1  试验工点纵断面图

Fig.1  Vertical section of test site

2.2  模型参数

在DK1252+679~DK1252+731段涵涵间短路基过渡段，工点为板式无砟轨道结构。轨下胶垫厚38 mm，弹簧系数k=4.38×10⁷ N/m，阻尼系数c=4.5×10⁴ N/(s·m)；轨枕间距l_s=0.6 m，轨距为1.435 m；两轨道中心线相距5.0 m。涵-涵过渡段1个框架涵孔径为1.8 m，净高2.4 m；另一个框架涵孔径4.2 m，净高2.7 m。整个计算长度取为74.4 m。其他计算参数见表1。

表1  涵-涵过渡段模型参数

Table 1  Model parameters of culvert-culvert transition section

该模型共定义4种单元：第1层钢轨为梁单元BEAM188；第2层钢轨是下垫层，无砟轨道的扣件系统都是采用弹性扣件系统，采用弹簧-阻尼单元COMBIN14；第3层轨道板采用塑性小应变壳单元SHELL143；第4层是CA砂浆层，采用壳单元和弹簧阻尼单元共同模拟；其他结构层均采用实体单元SOLID45。所建立的实体有限元模型见图2。

图2  过渡段有限元模型

Fig.2  Finite element model of transition section

2.3  模态分析

模态分析可以用于确定1个结构或者机器部件的固有振动特性(固有频率、振型和阻尼比)，也可以是另一个动力学分析的出发点(如瞬态动力学分析、谐响应分析或者谱分析等)。固有频率和振型是承受动态载荷结构设计中的重要参数，如果要进行模态叠加法谐响应分析或瞬态动力学分析，固有频率和振型也是必要的。

1个具有n个自由度的体系，其振动方程可表示为：

        (1)

式中：[M]为质量矩阵；[C]阻尼矩阵；[K]为刚度矩阵，均为n阶方阵；，和{u}分别为加速度向量、速度向量和位移向量；{F(t)}为动荷载向量，进行模态分析时，{F(t)} =0。

模态分析时提取模态的方法有7种：分块兰索斯法(Block Lanczos)，子空间迭代法(Subspace)，缩减法(Reduced)，PowerDynamics法，非对称法(Unsymmetric)，阻尼法(Damped)和QR阻尼法(QR Damped)。本文采用分块兰索斯法对模态进行扩展，通过模态分析，建立的轨道和轨下结构系统的前2阶竖向固有频率分别为20.4 Hz和28.7 Hz。

3  路基振动测试分析

3.1  环境激励下振动测试

地脉动测试技术最初由日本提出，20世纪50年代引入我国，现在已发展成为一种较成熟的原位测试技术。它是由随机振源激发并经场地不同性质的岩土层界面多次反射和折射后传播到场地地面的振动；同时，地脉动不同的频幅变化和作用历时，会引起岩土体的不同响应。环境激励振动试验具有无须贵重及笨重的激励设备、不中断结构的正常使用、方便、省时等优点。

为准确测试过渡段路基自振频率，在试验段路基多处位置埋设传感器进行振动测试。本文主要以DK1252+703基床表层顶面与底面传感器的动力响应为例进行说明。图3所示为基床表层底面环境激励下路基振动加速度时程曲线。通过对时程曲线进行快速傅里叶变换，并加汉宁窗抑制泄露，所得功率谱曲线如图4所示。从图4可以看出：路基的前2阶自振频率分别为22.6 Hz和29.7 Hz。

图3  加速度时程曲线

Fig.3  Time history of acceleration

图4  自功率谱分析结果

Fig.4  Analysis result of auto-power spectrum

采用频域峰值法识别结构模态参数时，人工选取峰值存在一定的主观性，若对功率谱的峰值选取不当，则会直接影响频率识别结果^[16]。在现场试验时，可同时记录2个测点的地脉动信号，从它们的互功率谱图上可读出某一峰值频率对应的相位差。根据随机振动模态分析理论，若相位差为0°或180°，则可判断该峰值频率为地基的自振频率，否则为脉动源的优势频  率^[6]。图5所示为基床表层底面与顶面测点互相关系数曲线，图6所示为基床表层底面与顶面测点互功率谱曲线。从图5可以看出：2个信号的相关程度很高。从图6可以看出：在22.6 Hz和29.7 Hz处相位差基本为0°，故可以认为判定是正确的。因此，可以用相位差作为依据，辅助选取结构自振频率。

图5  互相关系数分析

Fig.5  Analysis of cross correlation coefficient

图6  互功率谱曲线

Fig.6  Curves of cross-power spectrum

3.2  最大熵谱(MEM)分析

峰值法需要主观判断峰值识别结构的频率。由于自然环境振动条件下路基的振动幅值很小，且快速傅里叶变换(FFT)不可能对无限长的序列进行运算，所以，必须对自相关函数进行截取，也就是所谓的加窗，这造成频谱的能量泄漏。在峰值比较密集或有虚假的峰值时，即使加上互功率谱相位差的辅助判据，也很难将结构系统的固有频率全部准确地识别出来^[10]。

对于传统谱估计，只有观测较长及数据采样点较多时，才能得到较高的谱估计精度。加窗可减少泄露，但也降低了频谱分辨率^[11]。与传统谱比较，最大熵谱(MEM谱)没有传统谱受到数据加窗所带来的一系列缺陷。由于它是连续谱，从理论上讲，谱光滑，谱峰陡峭，频率分辨力很大。最大熵谱表达式为^[17]：

       (3)

式中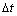：为采样间隔；r_k为预测误差滤波器的系数；P_m为预测误差的方差。

当高速列车通过路基时，引起结构产生强迫振动；当列车驶离后，路基恢复到静力平衡位置时仍在振动，这时的结构作衰减自由振动。由于此时路基的振动幅值比环境激励情况下的振动幅值大，所以，这时测试路基的自振频率效果比较理想。但由于其衰减较快，衰减时间较短，采样长度有限，故适合于采用最大熵谱法对自由衰减振动进行频谱分析，从而得到较准确的测试结果。图7所示为基床表层底面在自由衰减时的最大熵谱分析结果；图8所示为基床表层顶面在作自由衰减振动时的最大熵谱分析结果。

从图7和图8可以看出：基床表层顶面与底面的最大熵谱分析图曲线基本一致，只是幅值有所变化，且频率峰值清晰，可以准确地判断其自振频率；路基的前2阶自振频率分别为22.8和29.8 Hz。这与模态分析、环境激励测试的结果基本一致，故采用最大熵谱法分析路基衰减自由振动可以得到较好的效果。

图7  基床表层底面最大熵谱

Fig.7  Maximal entropy spectrum of bottom surface layer of subgrade

图8  基床表层顶面最大熵谱

Fig.8  Maximal entropy spectrum of top surface layer of subgrade

4  结论

(1) 通过对过渡段有限元模型进行模态分析，所得路基自振频率与现场实测分析结果基本相近。这说明在理论模型准确的前提下，可以采用模态分析方法计算路基自振频率，从而节省较昂贵的现场测试费用。

(2) 采用环境激励方法识别过渡段路基自振频率时，可以采用2个测点互功率谱图上某一峰值频率对应的相位差作为依据，辅助选取结构自振频率，以避免选取脉动源的优势频率作为自振频率。

(3) 当高速列车驶离路基后，路基恢复到静力平衡位置时仍在作衰减自由振动，此时，路基的振动幅值比环境激励情况下的振动幅值大。采用最大熵谱法对衰减自由振动进行频谱分析，可以更易于获得其固有频率，从而得到较准确的测试结果。

参考文献：

[1] Kerr A D. 轨道力学及轨道工程[M]. 上海铁道学院教研室, 译. 北京: 中国铁道出版社, 1988: 199-215.
Kerr A D. Track mechanics and track engineering[M]. Teching Room of College of Shanghai Railway, trans. Beijing: China Railway Publishing House, 1988: 199-215.

[2] Grassie S L. Track deflections and macroscopic movement of railway embankment[J]. Vehicle System Dynamics Supplement, 1995, 24: 154-163.

[3] Ah1beck O R. Effects of track dynamics impedance on vehicle-track interactions[J]. Vehicle System Dynamics Supplement, 1995, 24: 58-71.

[4] 聂志红, 李亮, 刘宝琛, 等. 秦沈客运专线路基振动测试分析[J]. 岩石力学与工程学报, 2005, 24(6): 1067-1071.
NIE Zhi-hong, LI Liang, LIU Bao-chen, et al. Testing and analysis on vibration of subgrade for Qinhuangdao-Shenyang Railway[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(6): 1067-1071.

[5] 卿启湘, 王永和, 赵明华. 秦沈客运专线路桥(涵)过渡段路基的动力特性分析[J]. 岩土力学, 2008, 29(9): 2415-2421.
QIN Qi-xiang, WANG Yong-he, ZHAO Ming-hua. Research on dynamic performance of bridge(culvert)—subgrade transition section on Qin-shen High-speed Railway[J]. Rock and Soil Mechanics, 2008, 29(9): 2415-2421.

[6] 陈龙珠, 吴世明, 魏玉伦. 用机械阻抗法求成层地基的固有频率[J]. 岩土工程学报, 1989, 11(2): 82-87.
CHEN Long-zhu, WU Shi-ming, WEI Yu-lun. Calculate the natural frequency of layered ground based on mechanical impedance method[J]. Chinese Journal of Geotechnical Engineering, 1989, 11(2): 82-87.

[7] 邓亚虹. 层状自由场地固有频率的求解方法、特性及应用研究[D]. 杭州: 浙江大学建筑工程学院, 2007: 20-50.
DENG Ya-hong. Research on solving methods, characteristics and applications of layered soil site's natural frequency[D]. Hangzhou: Zhejiang University. Architecture Engineering College, 2007: 20-50.

[8] 杨学林, 陈云敏, 蔡袁强, 等. 利用地脉动确定地基自振频率[J]. 岩土工程学报, 1995, 17(4): 51-55.
YANG Xue-lin, CHEN Yun-min, CAI Zhi-qiang, et al. Determination of the natural frequencies of soil deposit by ground microtremors[J]. Chinese Journal of Geotechnical Engineering, 1995, 17(4): 51-55.

[9] 卿启湘, 王永和, 赵明华, 等. 高速移动载荷作用下板式轨 道-软岩路基系统的动力特性分析[J]. 岩土力学, 2008, 29(5): 1396-1402.
QING Qi-xiang, WANG Yong-he, ZHAO Ming-hua, et al. Research on dynamic characteristics of slab track-roadbed systems with soft rock as embankment filling under high speed moving load[J]. Rock and Soil Mechanics, 2008, 29(5): 1396-1402.

[10] 胡萍, 王永和, 卿启湘. 改良土过渡段基床底层的动力特性分析[J]. 中南大学学报: 自然科学版, 2009, 40(6): 1705-1711.
HU Ping, WANG Yong-he, QING Qi-xiang. Dynamic performance of bridge approach subgrade with improved soil as base course[J]. Journal of Central South University: Science and Technology, 2009, 40(6): 1705-1711.

[11] 卿启湘. 高速铁路无砟轨道-软岩路基系统动力特性研究[D]. 长沙: 中南大学土木建筑学院, 2005: 10-40.
QING Qi-xiang. Study on dynamical characteristics in soft zone for ballastless tracks on high aped railway[D]. Changsha: Central South University. School of Civil and Architecture Engineering, 2005: 10-40.

[12] 曹新文, 蔡英. 铁路路基动态特性的模型试验研究[J]. 西南交通大学学报, 1996, 31(1): 36-41.
CAO Xin-wen, CAI Ying. A model test study of the dynamic performance of subgrade[J]. Journal of Southeast Jiaotong University, 1996, 31(1): 36-41.

[13] 蔡成标, 翟婉明, 赵铁军, 等. 列车通过路桥过渡段时的动力作用研究[J]. 交通运输工程学报, 2001, 1(1): 17-20.
CAI Cheng-biao, ZHAI Wan-ming, ZHAO Tie-jun. et al. Research on dynamic interaction of train and track on roadben-bridge transition section[J]. Journal of Traffic and Transportation Engineering, 2001, 1(1): 17-20.

[14] 王开云, 蔡成标, 徐志胜. 基于频域方法的轨道随机振动特性及试验验证分析[J]. 机械工程学报, 2005, 41(11): 149-152.
WANG Kai-yun, CAI Cheng-biao, XU Zhi-sheng. Analysis of random vibration characteristics and verification of track sructuue on frequency domain method[J]. Chinese Journal of Mechanical Engineering, 2005, 41(11): 149-152.

[15] 翟婉明. 车辆-轨道耦合动力学[M]. 北京: 中国铁道出版社, 2002: 50-85.
ZHAI Wan-ming. Vehicle-track coupling dynamics[M]. Beijing: China Railway Press, 2002: 50-85.

[16] 禹丹江. 土木工程结构模态参数识别[D]. 福州: 福州大学土木工程学院, 2006: 20-50.
YU Dan-jiang. Modal parameter identification of civil engineering structures[D]. Fuzhou: Fuzhou University. College of Civil Engineering, 2006: 20-50.

[17] 张文泉, 李彦斌. 最大熵谱估计及应用研究[J]. 现代电力, 2001, 18(15): 41-46.
ZHANG Wen-quan, LI Yan-bin. Maximum entropy spectrum estimation and its application[J]. Modern Electric Power, 2001, 18(15): 41-46.

(编辑 陈灿华)

收稿日期：2011-05-20；修回日期：2011-07-25

基金项目：国家自然科学基金资助项目(50678177)；铁道部科技研究开发计划项目(2005K002-B-1)

通信作者：陈湘亮(1974-)，男，湖南新宁人，博士研究生，从事路基动力特性的教学与研究工作；电话：13508473429；E-mail: cxlwch425@163.com