铜板带的连挤连轧成形速度
来源期刊:中国有色金属学报(英文版)2013年第4期
论文作者:运新兵 游伟 赵颖 李冰 樊志新
文章页码:1108 - 1113
关键词:铜板带;连挤连轧;咬入条件;速度协调方程
Key words:copper strip; continuous extrusion and rolling; bite condition; compatibility equation of velocity
摘 要:结合连续挤压和轧制技术,提出一种铜板带生产新技术——连挤连轧成形工艺。在连挤连轧成形过程中,保证轧制速度与连续挤压速度的匹配是实现连挤连轧成形的重要条件。通过塑性力学理论计算,确定连续挤压咬入条件,建立轧辊转速与挤压轮转速、压下量和板带尺寸等参数之间的协调方程。以TLJ400连续挤压机及直径为200 mm的轧辊为模型,建立连挤连轧成形的有限元模型,并利用DEFORM-3D软件对铜板带连挤连轧成形过程进行数值模拟,研究连续挤压与轧制速度的关系,验证连挤连轧速度协调方程的准确性。
Abstract: A new copper strip production technology combined with continuous extrusion and rolling technology was proposed. The roll velocity must first be matched with the continuous extrusion velocity to achieve continuous extrusion and roll forming. The bite condition of continuous extrusion was determined, and the compatibility equation between the roll velocity and parameters such as the extrusion wheel velocity, reduction, and strip size was established through mechanical by plastic theoretical calculations. The finite element model of continuous extrusion and rolling was then established by using the TLJ400 continuous extrusion machine with a roll diameter of 200 mm. The relationship between the continuous extrusion and rolling velocities was determined through numerical simulations by software DEFORM-3D, and the accuracy of compatibility equation of velocity was verified.
Trans. Nonferrous Met. Soc. China 23(2013) 1108-1113
Xin-bing YUN, Wei YOU, Ying ZHAO, Bing LI, Zhi-xin FAN
Engineering Research Center of Continuous Extrusion, Ministry of Education, Dalian Jiaotong University, Dalian 116028, China
Received 28 August 2012; accepted 25 October 2012
Abstract: A new copper strip production technology combined with continuous extrusion and rolling technology was proposed. The roll velocity must first be matched with the continuous extrusion velocity to achieve continuous extrusion and roll forming. The bite condition of continuous extrusion was determined, and the compatibility equation between the roll velocity and parameters such as the extrusion wheel velocity, reduction, and strip size was established through mechanical by plastic theoretical calculations. The finite element model of continuous extrusion and rolling was then established by using the TLJ400 continuous extrusion machine with a roll diameter of 200 mm. The relationship between the continuous extrusion and rolling velocities was determined through numerical simulations by software DEFORM-3D, and the accuracy of compatibility equation of velocity was verified.
Key words: copper strip; continuous extrusion and rolling; bite condition; compatibility equation of velocity
1 Introduction
Over the last ten years, China has been the largest copper plate- or strip-consuming country in the world [1]. However, the production capacity and output of high-precision and specialized copper strip components cannot satisfy the growing needs of the market because of the relatively undeveloped production technology and equipment in China.
At present, the two common methods of manufacturing copper plates or strips are semicontinuous ingot hot-rolled cogging and horizontal continuous casting billet [2]. The subsequent processing steps for the two methods are the same. The process flow is as follows: face milling of the plate (or strip), followed by blooming, annealing, precise rolling, finishing, and finally obtaining the finished product. The deficiencies of these methods are as follows: 1) high energy consumption because of billet preheating as well as the high oxygen content of the product; 2) difficulty in eliminating the cast structural defects of horizontal continuous casting; 3) poor surface quality of traditional copper production because of the method of obtaining the strip billet, in this case, face milling or peeling processes are needed to eliminate surface defects (face milling can remove surface oxidation and surface cracking during the rolling process, whereas the section lines are removed during the continuous casting process); 4) necessity for multiple production procedures, long process flow, high equipment investment, and large space; and (5) difficulty in achieving a flexible production.
To address these issues, in this work, the continuous extrusion and roll forming technology for the production of oxygen-free copper plates or strips was presented. The process is listed below: upward cast rod—continuous extrusion and rolling—finishing—finished product. After friction drive was applied to the rod billet through continuous extrusion using a wheel groove, the upward cold-state, oxygen-free, cast rod was placed in the die cavity as a raw material to induce rapid and intense plastic deformation. Thus, the temperature of the billet increased from 600 to 800 °C to complete the continuous extrusion thermal deformation. Hot rolling was performed at the exit of the die, in which the heat that remained after the continuous extrusion was used as the thermal energy for the hot-roll. The principle of the deformation process is shown in Fig. 1.
Compared with traditional processes, the proposed process method has the following advantages: 1) The heating process is eliminated. Deformation heat and friction heat are used to reach the thermal deformation temperature of the material and complete the extrusion and roll forming process. In this process, the frictional resistance for energy dissipation is transferred into the deformation driving force and maximizes the use of energy. 2) The upward continuous casting process is used to reduce the oxygen content in the casting rod structure to lower than 2×10-5. Therefore, an oxygen-free copper strip with a pure structure is obtained. 3) The continuous extrusion and rolling both completely achieve the thermal deformation of the billet, during which the dynamic recrystallization occurs. Therefore, the grain is significantly refined and the material property is improved; however, the size of the billet is nearly the same as that of the finished product, thus reducing the workforce of the finishing process.
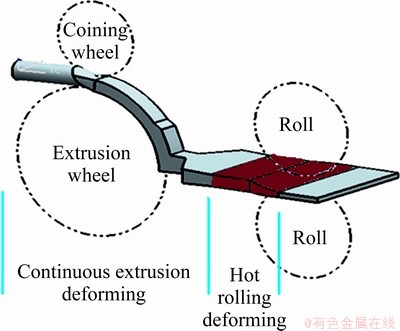
Fig. 1 Principle of continuous extrusion and rolling
FAN et al [3] established a new five-zone description model for the continuous extrusion process based on the state of the metal in the groove and provided its analytical solution through stress calculations for each subzone. YUN et al [4] divided the continuous extrusion extending cavity into the first extending region, second extending region, and deformation region. They established the dynamic models of the extrusion force for each region and derived the correlation between the specific extrusion force at the inlet of the extending cavity and the complicated coefficient for the part and section shape sizes. WU et al [5] investigated the effect of the extrusion wheel angular velocity on the continuous extrusion of copper concave bus bar formation. YUN et al [6] used numerical simulations to determine the metal flow regularity during the continuous extrusion formation. Meanwhile, LUO et al [7] investigated the deformation behaviour of a copper cladding aluminium wire during the flat rolling. The effects of the major process parameters on the deformation were analyzed by a 3D rigid plastic finite element model as well as experiments. XU and ZHU [8] used a thermal mechanical simulator to investigate the differences in titanium ingots as a result of forging and rolling.
Given the relatively recent introduction of continuous extrusion and rolling, no research on the mechanism, technical features, and process requirements of this process has been reported so far. In this work, the compatibility equation for the continuous extrusion and roll forming velocity was established to determine the relationship between the roll velocity and parameters such as extrusion wheel velocity, reduction, and strip size. Numerical simulations were performed using the DEFORM-3D software platform to analyze the relationship between the continuous extrusion and the roll-forming velocity of the copper strip.
2 Establishment of compatibility equation for continuous extrusion and rolling velocity
2.1 Calculation of velocity of billet entry into wheel groove
2.1.1 Determination of biting condition
The biting process of the continuous extrusion can be equated with that of the reduction in the single-roller drive roll [9,10] based on their characteristics. Figure 2 shows that the biting condition of continuous extrusion is
 (1)
(1)
where α1 is the biting angle between the billet and the extrusion wheel; R1 is the radius of the extrusion wheel; R2 is the radius of the coining wheel; β is the friction angle between the extrusion wheel surface and the billet surface; and θ is the friction angle between the coining wheel and the billet.
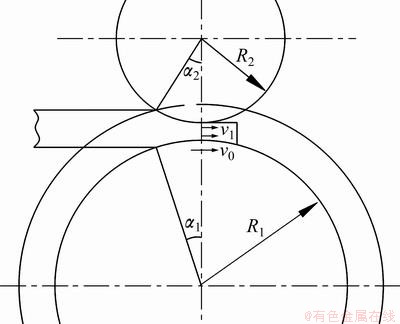
Fig. 2 Biting process of continuous extrusion
2.1.2 Velocity calculation
In the biting process, the velocity v1 of billet entry into the wheel groove is higher than the linear velocity v0 of the extrusion wheel at this position. The ratio of the difference between v1 and v0 to the linear velocity v0 of the extrusion wheel is the forward slip value [11], which is expressed by
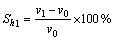 (2)
(2)
The forward slip value is calculated by
 (3)
(3)
Based on the two simultaneous equations, we obtain
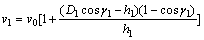 (4)
(4)
where D is the diameter of the extrusion wheel; γ1 is the neutral angle,
 ;
;
μ1 is the friction coefficient between the billet and the extrusion wheel surface; and h1 is the height of the billet after biting.
2.2 Calculation of billet velocity at die exit
The billet enters the cavity for expansion via the wheel groove and is finally extruded from the die exit. This process does not consider the billet overflow. According to the same flow per time and volume [12],
 (5)
(5)
where F1 is the pass cross-sectional area between the extrusion wheel and the coining wheel, and F2 is the cross-sectional area of the die exit.
The billet exit velocity from the die exit can be obtained by
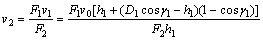 (6)
(6)
2.3 Calculation of roll velocity
The strip is extruded from the die exit at velocity v2. The velocity of the strip entry into the roll gap in the absence of tension is equal to that at the strip die exit (Fig. 3). In the rolling process, the following equation can be obtained using the same flow per time and volume:
 (7)
(7)
where FH is the cross-sectional area of the strip at the roll entrance; Fh is the cross-sectional area of the strip at the roll exit; vH is the entry velocity of the strip into the roll gap; and vh is the exit velocity of the strip from the roll gap.
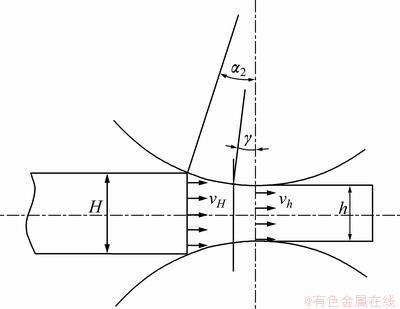
Fig. 3 Schematic diagram of velocity in rolling process
According to the definition of the forward slip value,
 (8)
(8)
where v is the peripheral roll velocity.
From the two simultaneous equations, we obtain
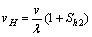 (9)
(9)
where  is the expansion coefficient of the strip.
is the expansion coefficient of the strip.
The forward slip value is calculated using the following equation:
 (10)
(10)
where D2 is the roll diameter; h is the sheet height after rolling; and γ2 is the neutral angle.
Based on the internal force equilibrium of the strip in the roll deformation zone force [13], we obtain
 (11)
(11)
where  is the biting angle in the rolling process; Δh is the roll reduction; and μ2 is the friction coefficient between the strip and the roll surface. By substituting Eq. (10) into Eq. (9), we obtain
is the biting angle in the rolling process; Δh is the roll reduction; and μ2 is the friction coefficient between the strip and the roll surface. By substituting Eq. (10) into Eq. (9), we obtain
 (12)
(12)
2.4 Establishment of compatibility equation for continuous extrusion and rolling velocities
As previously stated, the rolling process is an on-line continuous rolling process combined with a continuous extrusion process. Thus, the roll velocity is affected by factors such as the reduction and the friction coefficient. Based on the equal volume deformation conditions, the compatibility equation between the roll and extrusion wheel velocities, the extrusion strip size, and roll reduction was established. Thus, the continuous extrusion and rolling process of the copper strip can proceed smoothly.
As previously mentioned, the entry velocity of the strip into the roll gap in the absence of tension is equal to the exit velocity of the strip from the die exit, which is expressed as
vH=v2 (13)
By substituting Eq. (6) into Eq. (12), the relation- ship between the roll and the extrusion wheel velocities, the extrusion strip size, and roll reduction is obtained:
 (14)
(14)
3 Numerical simulation and analysis of results
The DEFORM-3D software was used for the numerical simulation of the continuous extrusion and rolling of a copper strip with the continuous extrusion. The following dimensions were set as: A=100 mm; B=10 mm; and R=5 mm (the cross-sectional shape is shown in Fig. 4). The thickness h is 8 mm after rolling.

Fig. 4 Cross-sectional shape of strip
3.1 Establishment of finite element model
The finite element model of the extrusion and roll with a diameter of 200 mm (Fig. 5) was established by a TLJ400 continuous extrusion machine. To save time and reduce the computer storage capacity, 1/2 of the integral model was used for the simulation based on the symmetry [14].
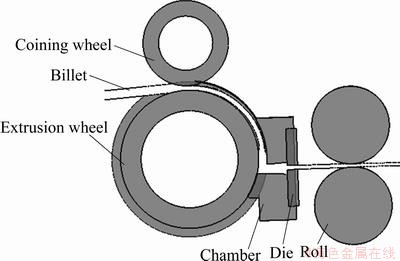
Fig. 5 Finite element geometric model
3.2 Selection of simulation parameters
The deformation material used for the simulation is pure copper. The tool and die materials are all AISI-H13. The rigid viscoplastic finite element method was used. The billet was set as the rigid-plastic body, whereas the die and other parts were set as rigid bodies. The shear friction driving model was used for the friction between the contact surfaces of the billet and the die. In this work, the friction coefficient between the extrusion wheel and the billet was set at 0.95, whereas the friction coefficient between the roller and the billet was set at 0.35. By considering the preheating of the cavity, the initial temperatures of the cavity, abutment, and die were set at 450 °C, whereas the preheating temperature of the roller was set at 60 °C [15-19].
3.3 Simulation results and analysis
In the continuous extrusion and rolling processes, the metal deformation was divided into six parts, namely, pass rolling, filling, upsetting, expansion extrusion, transition, and roll forming zones (Fig. 6).
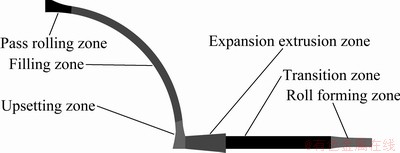
Fig. 6 Division of forming zones
3.3.1 Verification of accuracy of compatibility equation for continuous extrusion and rolling velocities
Equation (14) was used to calculate the roll velocity at extrusion wheel velocities of 4, 6, 8, and 10 r/min which correspond to horizontal linear velocities of 74.5, 111.78, 149.05, and 186.3 mm/s, respectively, for the numerical simulations. The results were then compared with the horizontal linear velocity of the billet at the roller exit after the theoretical calculations.
Figure 7 shows a comparison of simulated and theoretical velocities of the billet at the roller exit. The simulation values are always less than those of the theoretical calculations because the theoretical values are calculated at the constant volume. The volume loss caused by the redivision of the mesh results in the lower simulation values compared with the theoretical ones. However, the errors are within 5%, which confirms the accuracy of the continuous extrusion and rolling velocity compatibility equation.
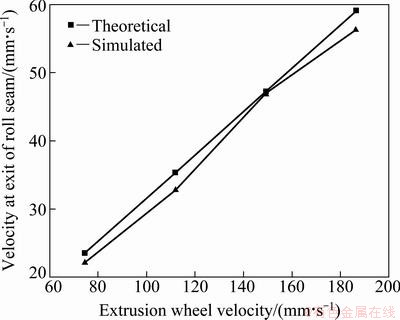
Fig. 7 Comparison between theoretical and simulated velocities
3.3.2 Velocity distribution at each stage of continuous extrusion and rolling process
The velocity distribution at each stage was obtained at the extrusion wheel velocity of 6 r/min (Fig. 8(a)). The velocity distribution in the pass rolling zone is lower because of the large friction between the billet and the extrusion wheel, whereas the metal flow velocity at the bottom of the wheel groove is 5 mm/s higher than that in the filing zone because of the adhesive friction. The billet moves with the rotation of the extrusion wheel, without plastic deformation, and the flow velocity is more uniform (Fig. 8(b)). In the upsetting zone, the metal flow direction changes because of the increase in the front resistance. In addition, the radial direction of the extrusion wheel is gradually filled until the entire wheel groove is full. In this velocity distribution, the velocity is reduced in the vertical direction because of the blocking of the abutment (Fig. 8(c)). Moreover, the billet accumulation occurs at a right-angle bending and the velocity is low. However, when the billet leaves the right-angle bending, a certain increase in the velocity occurs. In the expansion extrusion zone, the metal flow is faster near the die exit, and the velocity of the gradual flow to the calibration bench tends to be smooth. The metal flow rate away from the centre as well as the cavity contact area is low because of the existence of a dead zone (Fig. 8(d)). In the transition zone, the metal is extruded from the die exit; this extrusion can be considered a rigid motion at a velocity of 23.7 mm/s. Figure 8(e) shows the velocity distribution in the roll forming zone. The velocity of the billet exiting from the roll is 8 mm/s higher than that of the billet entering into the roll because of the forward slip phenomenon in the roll zone. In addition, the metal flow in the entire metal zone is more uniform. After the metal flows out of the roll, most of the metal flow velocity is consistent and stable. This velocity can be considered a rigid body movement at a velocity of 33 mm/s.
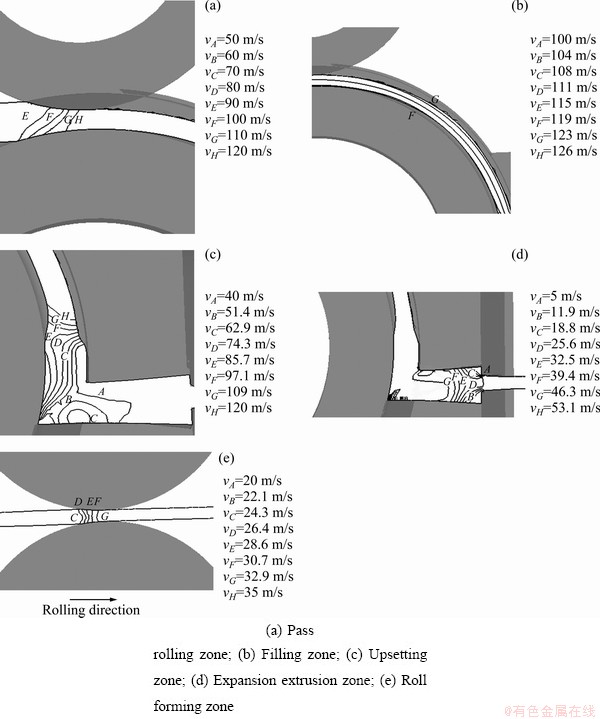
Fig. 8 Distribution of velocity at each stage of continuous extrusion and rolling
4 Conclusions
1) The bite condition of continuous extrusion was determined through theoretical calculations.
2) A compatibility equation for the continuous extrusion and roll forming velocities was established.
3) The relationship between the continuous extrusion and rolling velocities was obtained. The accuracy of the compatibility equation for the continuous extrusion and rolling forming velocities was verified by numerical simulations.
References
[1] WANG Bi-wen. Steady development of China’s copper processing industry in the face of adversity [J]. Chinese Journal of Nonferrous Metals, 2010(6): 1-2. (in Chinese)
[2] WANG Bi-wen. Strip production and the market of copper and copper alloy(continued) [J]. Journal of World Non-ferrous Metals, 2008(1): 34-35. (in Chinese)
[3] FAN Zhi-xin, SONG Bao-yun, LIU Yuan-wen, YUN Xin-bing. Deformation model and stress distribution of continuous extrusion process [J]. The Chinese Journal of Nonferrous Metals, 2007, 17(2): 283-289. (in Chinese)
[4] YUN Xin-bing, WU Yang, YOU Wei, ZHAO Ying, CHEN Li, SONG Bao-yun. Research on mechanical model of continuous extrusion with two-step extending forming for copper strip [J]. Journal of Plasticity Engineering, 2012, 19(3): 13-19. (in Chinese)
[5] WU Peng-yue, XIE Shui-sheng, LI Hua-qing. Effect of extrusion wheel angular velocity on continuous extrusion forming process of copper concave bus bar [J]. Transactions of Nonferrous Metals Society of China, 2007, 17(2): 280-286.
[6] YUN Xin-bing, YAO Ming-liang, WU Yang, SONG Bao-yun. Numerical simulation of continuous extrusion extending forming under the large expansion ratio for copper strip [J]. Applied Mechanics and Materials, 2011, 80-81: 91-95.
[7] LUO Yi-bing, LIU Xin-hua, XIE Jian-xin. Numerical simulation and experimental investigation on rolling behaviors of copper cladding aluminum flat wires [J]. The Chinese Journal of Nonferrous Metals, 2009, 19(7): 1245-1251. (in Chinese)
[8] XU Chun, ZHU Wen-feng. Comparison of microstructures and mechanical properties between forging and rolling processes for commercially pure titanium [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(8): 1939-1946.
[9] CHU Hua-qing. The essence of bite process and the role of post-thrust [J]. Journal of Anshan Technology University, 1980, 2: 64-72. (in Chinese)
[10] ZHENG Wan-cheng. Inquiry about bite condition of dissymmetric heterodiameter rolling mill with single-roll-driving [J]. Hebei Metallurgy, 1995, 3: 27-29, 48. (in Chinese)
[11] ZHANG Xiao-ping. Roll theory [M]. Beijing: Metallurgical Industry Press, 2006: 159-161. (in Chinese)
[12] WANG Ting-pu, QI Ke-min. Metal plastic processing-roll on theory and technology [M]. Beijing: Metallurgical Industry Press, 2001: 38-39. (in Chinese)
[13] YANG Zong-yi. Technical manual of practical roll [M]. Beijing: Metallurgical Industry Press, 1994: 194-195. (in Chinese)
[14] XIE Shui-sheng, LI Lei. FEM of metal plastic forming process [M]. Beijing: Metallurgical Industry Press, 1994: 247-248. (in Chinese)
[15] LIU Ming-yue, SONG Bao-yun, YUN Xin-bing. Numerical simulation of continuous extrusion extending forming process for copper busbar based on FEM [J]. Journal of Thermal Processing, 2008, 9: 72-75. (in Chinese)
[16] CHO J R, JEONG H S. Parametric investigation on the curling phenomenon in conform process by three-dimensional finite element analysis [J]. Mater Process Technol, 2001, 110: 53-60.
[17] YUN Xin-bing, CHEN Xu, ZHAO Ying, FAN Zhi-xin, SONG Bao-yun. Effect of the die and tool structure on continuous extrusion expansion forming of copper [J]. Materials Science Forum, 2012, 704-705: 196-202.
[18] LEE J D, CHEN Y P. Non-steady-state elastic-plastic behavior of metal forming(roll) with a generalized friction law [J]. Theoretical and Applied Fracture Mechanics, 2000, 33: 93-99.
[19] CHEN Li, SONG Bao-yun, YUN Xin-bing. Numerical simulation of the effect of feedstock shape on continuous extrusion process [J]. Advanced Materials Research, 2012, 472-475: 2004-2008.
运新兵,游 伟,赵 颖,李 冰,樊志新
大连交通大学 连续挤压教育部工程研究中心,大连 116028
摘 要:结合连续挤压和轧制技术,提出一种铜板带生产新技术——连挤连轧成形工艺。在连挤连轧成形过程中,保证轧制速度与连续挤压速度的匹配是实现连挤连轧成形的重要条件。通过塑性力学理论计算,确定连续挤压咬入条件,建立轧辊转速与挤压轮转速、压下量和板带尺寸等参数之间的协调方程。以TLJ400连续挤压机及直径为200 mm的轧辊为模型,建立连挤连轧成形的有限元模型,并利用DEFORM-3D软件对铜板带连挤连轧成形过程进行数值模拟,研究连续挤压与轧制速度的关系,验证连挤连轧速度协调方程的准确性。
关键词:铜板带;连挤连轧;咬入条件;速度协调方程
(Edited by Wei-ping CHEN)
Foundation item: Project (51175055) supported by the National Natural Science Foundation of China; Project (201102020) supported by the Natural Science Foundation of Liaoning Province, China; Project (2011BAE23B01) supported by the National Key Technology R&D Program of China
Corresponding author: Xin-bing YUN; Tel: +86-411-84109416; E-mail: yunxb@djtu.edu.cn
DOI: 10.1016/S1003-6326(13)62572-8

