J. Cent. South Univ. (2017) 24: 168-177

DOI: 10.1007/s11771-017-3418-8

Rock strength interval analysis using theory of testing blind data and interval estimation

TIAN Sen(田森)^{1, 2, 3}, CHEN Jian-hong(陈建宏)³, DONG Long-jun(董陇军)³

1. State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University,

Chongqing 400044, China;

2. School of Resources and Environmental Science, Chongqing University, Chongqing 400044, China;

3. School of Resources and Safety Engineering, Central South University, Changsha 410083, China

 Central South University Press and Springer-Verlag Berlin Heidelberg 2017

Abstract: The concepts of rock strength intervals are presented in this work, furthermore, central values of intervals and their corresponding credibility are provided using two-case study based on blind data theory and fuzzy interval estimation. 60 granite specimens are first tested, the compressive strength interval and tensile strength interval are [103.68, 219.61] and [7.53, 11.86] MPa, while the tested mean values of compressive strength and tensile strength are 152.86 and 10.14 MPa, the credibilities are less than 58.4% and around 70.4%, respectively, the credibility of shear strength is between 40% and 60%. Then 70 other rock specimens are designed and tested, the similar conclusions can be reached. The results show that the conventional definite values are the particular values within the intervals, and the credibility of them often fails to reach the high-precision engineering requirement. The results demonstrate the feasibility and application potential of this proposed algorithm for the engineering practice. The references for engineering value selection of rock strength under different credibility or according to frequency distribution of central values are provided to increase the reliability and precision of calculation.

Key words: rock strength interval; uniaxial compressive strength; uniaxial tensile strength; shear strength; blind data; interval theory

1 Introduction

In many engineering research projects, it is necessary to measure rock mechanical parameters of mining district through laboratory experiment or field tests [1–3], especially in mining engineering. Rock strength is important mechanics parameter of rock mass for engineering design and calculation; it mainly consists of compressive strength, tensile strength and shear strength. Current measurements of comprehensive strength, tensile strength and shear strength are determined according to suggested methods for determining rock strength and regulations of physical and mechanical tests [4–12] compiled by International Society for Rock Mechanics (ISRM) and the American Society for Testing Materials (ASTM), and mean value of several groups of rock samples is often adopted, however, it does not consider measurement, calculation errors even distortion in test process [13].

For this purpose, the concepts and computing methods of rock compressive strength interval, tensile strength interval and shear strength interval are put forward in this work. Furthermore, central values of intervals and their corresponding credibility are provided using two-case study to fit features of the tests finiteness, randomness, and reflect the possible values distribution of the rock strength intervals based on blind data theory and fuzzy interval estimation [14–16]. Two cases are chosen and several groups of rock specimens are designed and tested.

2 Theory and method

2.1 Rock strength parameters

This work mainly studies on the interval expressions of the uniaxial compressive strength, the uniaxial tensile strength and the shear strength parameters, the conventional concepts and the calculation formulas of them are given firstly, as shown below.

2.1.1 Uniaxial compressive strength

Under uniaxial compression condition, the maximum compressive stress that rock mass can withstand is referred to as rock uniaxial compressive strength, the calculation formula is given [17]:

If the shape of specimen is in a cylinder shape, then

                                   (1)

If the shape of specimen is in a cube shape, then

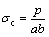                                    (2)

where p is the failure load under uniaxial compression, d is sample diameter of the cross section, a and b refer to sample cross-sectional length and width respectively.

2.1.2 Uniaxial tensile strength

Under uniaxial extension condition, the maximum tensile tress that rock mass can withstand is referred to as rock uniaxial tensile strength, and the calculation formula is given [18, 19]. The tensile strength parameters are usually obtained using Brazilian splitting test [20–22].

If the shape of specimen is in a cylinder shape, then

                                   (3)

If the shape of specimen is in a cube shape, then

                                   (4)

where p is the failure load under uniaxial extension, d is sample diameter of the cross section, t is sample thickness, a and b refer to sample cross-sectional length and width.

2.1.3 Shear strength

Under shear load condition, the maximum shear stress that rock mass can withstand is referred to as rock shear strength, where the calculation formula is presented by Coulomb theory. The estimates of shear strength are obtained from direct shear tests in this work as discussed in details by ALONSO et al [23] and BARLA et al [24], they inherently account for any possible scale effect.

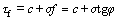                          (5)

where σ is the normal pressure of the shearing surface, c is the cohesion, f is the friction coefficient, φ is the friction angle, and σf is sample anelasticity.

2.2 Rock strength interval

Then the expressions of rock strength intervals along with the computing methods are created in the following section.

2.2.1 Uniaxial compressive strength interval

Uniaxial compressive strength interval is defined as [], Eqs. (1) and (2) can also be expressed as follows:

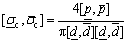                        (6)

                          (7)

where  denotes the failure load interval under uniaxial compression,  is sample diameter of the cross section interval, and refer to the interval of sample cross-sectional length and width. When, the interval becomes a definite value, thus it can be seen that the mean value of compressive strength is just a particular value within the interval.

2.2.2 Uniaxial tensile strength interval

Uniaxial tensile strength interval is defined as [], Eqs. (3) and (4) can also be expressed as follows:

                        (8)

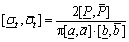                        (9)

wheredenotes the failure load interval under uniaxial extension, is sample diameter interval of the cross section, is sample thickness interval, and refer to the interval of sample cross-sectional length and width. Likewise, it also can be seen that mean value of tensile strength is a particular value within the interval.

2.2.3 Shear strength interval

Shear strength interval is defined as, the expression is given as

     (10)

where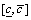denotes the cohesion interval, is the friction coefficient interval, 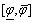is the friction angle interval of specimens. Of course, conventional constant values of shear strength parameters are also the particular values within their intervals.

2.3 Blind date theory

Based on current research on interval analysis, the blind data theory is proposed to overcome this problem. Blind data is used to express and handle a great variety of unascertained information mathematic tools [25, 26], and it can be applied to the calculations of rock strength intervals.

2.3.1 Expressions of blind data

Suppose a_i∈g(I), β_i∈[0, 1], and g(I) is interval grey number group composed of a series of grey number a_i, f(x)are used as grey function defined in g(I).

                (11)

When i≠j, a_i≠a_j, and f(x) is used as blind data, and it can be expressed as {[a₁, a_n], f(x)}, β_i is the credibility of a_i, β is total credibility of f(x), and n is the order of f(x), [a₁, a_n] is interval diameter, then f(x) is the credibility of interval diameter.

2.3.2 Credibility calculation of blind data

Suppose A and B are blind data, the detailed process of four arithmetic operations for blind data is shown by QIU and ZHANG [27] and GRZEGORZEWSKI [28]. And suppose * is any sign of four arithmetic operations, the element on row i and column j in A*B probable value matrix is corresponding with the element on row i and column j in A*B credibility product matrix. Arrange all elements in A*B probable value matrix in a list from small to large order as z₁, z₂, …, z_k, the same elements must be counted once, and list the corresponding elements in A*B credibility product matrix as c₁, c₂, …, c_k, among them:

  (12)

   (13)

where [z₁, z_k], D(z) and β(z) denote possible value interval, credibility density function and credibility of A*B respectively.

3 Calculations and results

3.1 Case 1

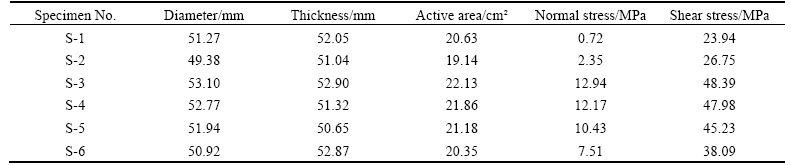
A China’s certain mine in Anhui Province, China is used to verify the applied feasibility of this method. The surface of this iron mine area is mainly covered with granite, the rock mechanics parameters in this mining district are not systematically measured yet. With the help of on-site engineers, the research group took several granite samples in July, September and November of 2013 respectively, and finally got 60 rock specimens through precise cutting, polish processing and design processing. We took 32 to 40 pieces of rock specimens for testing, specimen number of mechanic tests as well as process requirements is conducted according to suggested laboratory methods [29, 30] compiled by ISRM.

The tests results are shown in Tables 1–3.

Table 1 Test parameters of compressive strength

Table 2 Test parameters of tensile strength

Table 3 Test parameters of shear strength

Based on the blind data theory [31–33] mentioned above, rock compressive strength interval can also be expressed as follows:

    (14)

where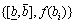and  are the blind data expression of sample length, width and compressive failure load. In this test, =[50.27, 54.66] mm, [50.02, 53.15] mm and = [301.22, 556.70] kN. Among them:

                    (15)

The compressive strength interval of granite is obtained as {[103.68, 219.61], f(σc)} through the blind data calculation of experiment data. The central values and corresponding credibility of compressive strength are shown in Table 4, where the bounds are consistent with the bounds of [103.68, 219.61] MPa, that are calculated by interval analysis theory [34, 35]. The frequency distribution of central values is shown in Fig. 1.

Based on the blind data theory [31-33], rock tensile strength interval can be expressed as follows:

   (16)

where and   are the blind data expression of sample diameter, thickness and tensile failure load. In this test, = [53.94, 54.76] mm, =[51.02, 54.64] mm, = [35.40, 51.46] kN. Among them:

                     (17)

The tensile strength interval of granite is obtained as [7.53, 11.86]. The central values and corresponding credibility of tensile strength are shown in Table 5. The frequency distribution of central values is shown in Fig. 2.

Likewise, Eq. (10) can also be expressed as follows:

   (18)

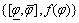where and  are the blind data expression of cohesion, friction coefficient and friction angle.

In this work, direct shear strength test is used to measure the rock shear strength parameters. There are also several methods to process and analyze the experiment data of shear strength parameters, to verify the validity of the proposed method, least square linear fitting of least square method is used to compare the result of the proposed method [36].

According to Mohr-Coulomb theory, to gain the shear strength parameters c, f and φ, several experimental data points (x_i, y_i) should be put into the rectangular coordinate system, where abscissa x-axis represents normal stress σ and ordinate y-axis represents shear stress τ, the slope and the y-intercept of the finally gained straight line is considered as the friction coefficient and cohesion.

In this work, six points are gained from Table 3 in the σ–τ rectangular coordinate system.

Table 4 Representative values and corresponding credibility of compressive strength

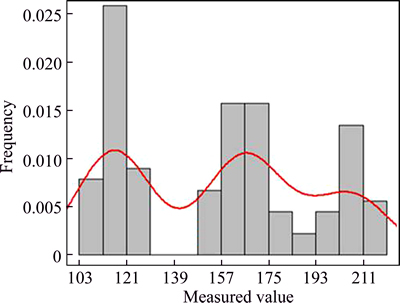
Fig. 1 Frequency distribution analysis

          (19)

Thus fifteen straight lines are obtained finally. Through the blind data calculation of experiment data, the shear strength parameters intervals of granite are obtained as: the cohesion interval =[19.73, 41.50],the friction coefficient interval =[0.53, 2.45], the friction angle interval =[27.92, 67.76]. The central values and corresponding credibility of shear strength parameters are shown in Table 6.

Table 5 Central values and corresponding credibility of tensile strength

Fig. 2 Frequency distribution analysis

3.2 Case 2

Take another gold mine in Shandong Province, China for example, the main rock types of this mining district are granitic cataclasite of sericitic alteration and granitic cataclasite of beresitization. We selected 70 pieces of representative processed rock specimens for testing, specimen numbers 1-6 denote granitic cataclasite of sericitic alteration, and numbers 7-12 denote granitic cataclasite of beresitization. The test results are shown in Tables 7–9.

Table 6 Central values and corresponding credibility of shear strength parameters

4 Analysis and discussion

Experimental mean value is often set as standard value in engineering practice for compressive strength and tensile strength, and shear strength parameters gained from least square regression line are often used as standard values in engineering practice.

In the first example, the compressive strength interval and tensile strength interval of granite are obtained as [103.68, 219.61] and [7.53, 11.86] MPa, relatively. The tested mean value of compressive strength is 152.86, its credibility is less than 58.4% according to Table 4; the mean value of tensile strength is 10.14, its credibility is around 70.4% according to Table 5, they are even inapplicable for the projects if high accuracy is required. The cohesion interval and the friction coefficient interval are 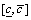=[19.73, 41.50] MPa and 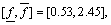the friction angle interval = [27.92, 67.76]. The credibility of least square regression line in Fig. 3 is between 40% and 60% according to Table 6, that is, these conventional constant values are relatively imprecise and unsafe for engineering calculation and design.

In the second example, the same as calculation process of the first case, the compressive strength interval and tensile strength interval of granitic cataclasite of sericitic alteration are obtained as [45.83, 94.79] and [2.81, 5.24] MPa, respectively, however, the mean values of the experimental data are 71.47 and  4.31 MPa, corresponding with the credibility only around 49.96% and 66.64%, respectively. The shear strength parameters intervals of granitic cataclasite of sericitic alteration are the cohesion interval =[9.21, 14.35] MPa, the friction coefficient interval  [0.48, 1.54] and the friction angle interval  [25.64, 57.0], the credibility of least square regression line of experimental data is only between 40% and 53.3%, as shown in Fig. 4.

The compressive strength interval and tensile strength interval of granitic cataclasite of beresitization are [18.68, 149.83] and [4.02, 9.97] MPa respectively, however, the mean values of the experimental data are 59.27 and 7.23 MPa, corresponding with the credibility only around 69.42% and 52.74%, respectively. The shear strength parameters intervals of granitic cataclasite of beresitization are: MPa, =[1.01, 1.68] and =[45.29, 59.24], the credibility of least square regression line of experimental data is between 40% and 46.7%, which is also shown in Fig. 4. These conventional definite values are also imprecise and unsafe for engineering calculation and design, especially in some high-accuracy demanding engineering calculation and design.

Table 7 Test parameters of compressive strength

Table 8 Test parameters of tensile strength

Table 9 Test parameters of shear strength

Fig. 3 Least square regression line of first sample

Fig. 4 Least square regression lines of second sample

In order to reduce the errors and reflect possible values of rock strength as much as possible, the concept of interval strength is put forward. We use rock strength intervals to describe rock sample size error and offset error resulted from experimenters’ reading and limited test condition. Strength interval and central value can fully describe rock strength parameter, decrease errors resulted from randomness and loaded state in tests, and it is more close to actual strength of rock mass than a definite value such as mean value.

5 Conclusions

The concepts of compressive strength interval, tensile strength interval and shear strength interval are presented. Through fuzzy interval estimation and blind data calculations of experimental data, the central values of rock strength intervals and their corresponding credibility are provided using two cases study to fit the features of laboratory tests finiteness, randomness, and reflect central values frequency distribution of rock strength intervals. 60 granite specimens are tested in case 1, the credibility of the conventional value of compressive strength, tensile strength and shear strength is less than 58.4%, around 70.4% and between 40% and 60%, relatively. Then 70 other pieces are tested, similar conclusions can be reached by taking case 2. The results show that the coverage of measured rock strength intervals is 100%. Compared with the results of conventional value selection methods, it is revealed that the credibility of these conventional constant values often fail to reach the high-precision engineering requirements.

A new and more comprehensive approach for value selection of rock strength parameters is established to improve the reliability and precision, which also considers laboratory reality and engineering practice.

Acknowledgments

The authors would like to acknowledge the Chinese Scholarship Council for their full scholarship of the first author’s two years study, as a joint PhD student in the University of Queensland, Australia. The authors would also like to acknowledge the State Key Laboratory of Coal Mine Disaster Dynamics and Control and the Deep Metal Mineral Exploitation and Hazard Control Key Laboratory and Geotechnical Engineering Centre colleagues for their help of on-site rock specimens’ extraction and processing.

References

[1] ZOU D H, CHENG Jiu-liu, YUE Ren-jie, SUN Xiao-yun. Grout quality and its impact on guided ultrasonic waves in grouted rock bolts [J]. Journal of Applied Geophysics, 2010, 72(2): 102–106.

[2] WANG Cheng, HE Wen, NING Jia-guo, ZHANG Chang-suo. Propagation properties of guided wave in the anchorage structure of rock bolts [J]. Journal of Applied Geophysics, 2009, 69(3, 4): 131–139.

[3] KHANDELWAL M, RANJITH P G. Correlating index properties of rocks with P-wave measurements [J]. Journal of Applied Geophysics, 2010, 71(6): 1–5.

[4] ASTM. American Society for testing and materials. Standard test method for unconfined compressive strength of intact rock core specimens [M]// Annual book of ASTM standards, 4.08. Philadelphia, Pennsylvania: ASTM, 1984.

[5] ASTM. Standard test method for splitting tensile strength of cylindrical concrete specimens [C]// Annual Book of ASTM, Standards. Philadelphia: ASTM, 1984, 42: 336.

[6] ASTM. Standard test method for performing laboratory direct shear strength tests of rock specimens under constant normal force [M]. West Conshohocken: ASTM International, 2008: 12.

[7] ISRM. Suggested method for determining point load strength [J]. Int J Rock Mech Min Sci Geomech, 1985, 22(2): 51–60.

[8] ISRM. Suggested methods for determining tensile strength of rock materials [J]. Int J Rock Mech Min Sci Geomech, 1978, 15(6): 99–103.

[9] ISRM. The complete ISRM suggested methods for rock characterization, testing and monitoring [J]. Environmental & Engineering Geoscience,2009,15(1): 47-48.

[10] ISRM. Suggested methods for determining the uniaxial compressive strength and deformability of rock materials [J]. Int J Rock Mech Min Sci, 1979,16(2): 135–140.

[11] SINGH T N, KAINTHOLA A, VENKATESH A. Correlation between point load index and uniaxial compressive strength for different rock types [J]. Rock Mech Rock Eng, 2012, 45(2): 259–264.

[12] MURALHA J, GRASSELLI G, TATONE B, BLUMEL M, CHRYSSANTHAKIS P, JIANG Yu-jing. ISRM suggested method for laboratory determination of the shear strength of rock joints: Revised version [J]. Rock Mech Rock Eng, 2014, 47(1): 291–302.

[13] ZHU Zhe-ming. Evaluation of the range of horizontal stresses in the earth's upper crust by using a collinear crack model [J]. Journal of Applied Geophysics, 2013, 88: 114–121.

[14] Alefeld G, Mayer G. Interval analysis: Theory and applications [J]. Journal of Computational and Applied Mathematics, 2000, 121(1, 2): 421–464.

[15] Bhattacharyya R, Kar S, Majumder D D. Fuzzy mean–variance–skewness portfolio selection models by interval analysis [J]. Computers and Mathematics with Applications, 2011, 61(2): 126–137.

[16] LAGRANGE S, DELANOUEA N D, JAULIN L. Injectivity analysis using interval analysis: Application to structural identifiability [J]. Automatica, 2008, 44(11): 2959–2962.

[17] Feng Xian-da, Jimenez R. Bayesian prediction of elastic modulus of intact rocks using their uniaxial compressive strength [J]. Engineering Geology, 2014, 173: 32–40.

[18] Erarslan N, Liang Zheng-zhao, Williams D J. Experimental and numerical studies on determination of indirect tensile strength of rocks [J]. Rock Mech Rock Eng, 2012, 45(5): 739–751.

[19] Erarslan N, Williams D J. Investigating the effect of cyclic loading on the indirect tensile strength of rocks [J]. Rock Mech Rock Eng, 2012, 45(3): 327–340.

[20] Claessona J, Bohlolib B. Brazilian test: Stress field and tensile strength of anisotropic rocks using an analytical solution [J]. International Journal of Rock Mechanics & Mining Sciences, 2002, 39(8): 991–1004.

[21] Fahimifar A, Malekpour M. Experimental and numerical analysis of indirect and direct tensile strength using fracture mechanics concepts [J]. Bull Eng Geol Environ, 2012, 71(2): 269–283.

[22] Carmona S, Aguado A. New model for the indirect determination of the tensile stress–strain curve of concrete by means of the Brazilian test [J]. Materials and Structures, 2012, 45(10): 1473–1485.

[23] ALONSO E E, PINYOL N M, PINEDA J A. Foundation of a gravity dam on layered soft rock. Shear strength of bedding planes in laboratory and large “in situ” tests [C]// 15th European Conf Soil Mechanics and Geotechnical Engineering. Athens, Greece: IOS Press, 2010: 389-394.

[24] BARLA G, ROBOTTI F, VAI L. Revisiting large size direct shear testing of rock mass foundations [C]// 6th International Conference on Dam Engineering. Lisbon, Portugal: LNEC, 2011: 15-17.

[25] WANG Xiao-jun, WANG Lei, QIU Zhi-ping. A feasible implementation procedure for interval analysis method from measurement data [J]. Applied Mathematical Modelling, 2014, 38(9, 10): 2377–2397.

[26] CHENG Hao-zhong, Zhu Hai-feng, Crow M L, Sheble G B. Flexible method for power network planning using the unascertained number [J]. Electric Power Systems Research, 2004, 68(1): 41–46.

[27] QIU Dong, ZHANG Wei-quan. Symmetric fuzzy numbers and additive equivalence of fuzzy numbers [J]. Soft Computing, 2013, 17(8): 1471–1477.

[28] Grzegorzewski P. Fuzzy number approximation via shadowed sets [J]. Information Sciences, 2013, 225(10): 35–46.

[29] ULUSAY R, HUDSON J A. The complete ISRM suggested methods for rock characterization, testing and monitoring [M]. Ankara, Turkey: ISRM Turkish National Group, 2007: 1974–2006.

[30] HAIMSON B, BOBET A. Introduction to suggested methods for failure criteria [J]. Rock Mech Rock Eng, 2012, 45(6): 973–974.

[31] Akbaria M G, Rezaeib A. Bootstrap testing fuzzy hypotheses and observations on fuzzy statistic [J]. Expert Systems with Applications, 2010, 37(8): 5782–5787.

[32] MA Li-hu, YAN Hui-zhe, ZHANG Yan-ni. Effectiveness evaluation of construction enterprise information systems planning based on unascertained number [J]. Procedia Engineering, 2011, 15: 4745–4750.

[33] ZHOU Tao, WANG Zeng-hui, YANG Rui-chang. Study on model of onset of nucleate boiling in natural circulation with subcooled boiling using unascertained mathematics [J]. Nuclear Engineering and Design, 2005, 235(21): 2275–2280.

[34] Aubrya C, Desmarea R, Jaulin L. Loop detection of mobile robots using interval analysis [J]. Automatica, 2013, 49(2): 463–470.

[35] YANG Yao-wen, CAI Zhen-han, LIU Yu. Interval analysis of dynamic response of structures using Laplace transform [J]. Probabilistic Engineering Mechanics, 2012, 29: 32–39.

[36] Das S K, Basudhar P K. Comparison of intact rock failure criteria using various statistical Methods [J]. Acta Geotechnica, 2009, 4(3): 223–231.

(Edited by FANG Jing-hua)

Cite this article as: TIAN Sen, CHEN Jian-hong, DONG Long-jun. Rock strength interval analysis using the theory of testing blind data and interval estimation [J]. Journal of Central South University, 2017, 24(1): 168-177. DOI: 10.1007/s11771-017-3418-8.

Foundation item: Project(2011DA105287—MS201605) supported by the State Key Laboratory of Coal Mine Disaster Dynamics and Control, China; Project(51374242) supported by the National Natural Science Foundation of China; Project(106112016CDJXY240004) supported by the Fundamental Research Funds for the Central Universities, China

Received date: 2016-01-29; Accepted date: 2016-05-17

Corresponding author: TIAN Sen, PhD, Lecturer; Tel: +86-17783691735; E-mail: sentian@cqu.edu.cn