DOI: 10.11817/j.issn.1672-7207.2016.08.021
基于傅里叶级数的多环反馈开关电流小波滤波器实现
李目1,吴笑锋1,席在芳1,何怡刚2
(1. 湖南科技大学 信息与电气工程学院,湖南 湘潭,411201;
2. 合肥工业大学 电气与自动化工程学院,安徽 合肥,230009)
摘要:提出一种基于傅里叶级数的多环反馈结构开关电流小波滤波器设计新方法。利用傅里叶级数法求取小波函数的时域小波逼近函数,以双输入多输出开关电流双线性积分器和单输入多输出电流镜作为基本单元设计相应的多环反馈结构小波滤波器,并通过调节开关电流滤波器的时钟频率获得不同尺度小波函数。对所设计的电路进行时域、频域和灵敏度分析,并研究元件非理想性对电路的影响。研究结果表明:该方法的小波逼近函数求取容易,滤波器电路具有设计简单、灵敏度低和受非理想性因素影响小的特点。
关键词:小波函数;傅里叶级数;函数逼近;开关电流滤波器;多环反馈结构
中图分类号:TN713 文献标志码:A 文章编号:1672-7207(2016)08-2694-07
Implementation of multiple-loop feedback switched-current wavelet filters based on Fourier series
LI Mu1, WU Xiaofeng1, XI Zaifang1, HE Yigang2
(1. College of Information and Electrical Engineering,
Hunan University of Science and Technology, Xiangtan 411201, China;
2. School of Electrical and Automation Engineering, Hefei University of Technology, Hefei 230009, China)
Abstract: A novel design method of switched-current (SI) wavelet filter with multiple-loop feedback (MLF) structure was presented based on Fourier series. The time domain wavelet function was approximated using Fourier series method. The wavelet filter whose impulse response was the approximated wavelet function was designed using MLF with bi-input-multi-output SI bilinear integrators and single-input-multi-output current mirrors as the basic building blocks. By changing the clock frequency, different scale wavelet functions were obtained. The time and frequency domain responses, sensitivity and influence of component imperfection of the wavelet filter circuit were analyzed. The results indicate that the proposed method has the features of easy wavelet approximation, simple filter circuit design, and low sensitivity and low imperfection influence.
Key words: wavelet function; Fourier series; function approximation; switched-current filter; multiple-loop feedback structure
小波变换作为一种良好的时频分析工具被广泛地应用于工程领域的信号处理,它是分析非平稳随机时变信号最有效的数学工具之一。由于传统的连续小波变换通常采用数字电路结合软件实现,难以满足低压、低功耗、实时和微型化的应用要求,因此,连续小波变换的模拟电路的实现成为国内外模拟信号处理领域研究的热点。目前,采用模拟电路实现连续小波变换方法主要有时域法和频域法。时域法是根据连续小波变换定义设计小波函数发生器、乘法器和积分器实现。由于设计产生不同尺度和位移小波簇的小波函数发生器难度很大,所以,采用时域法实现连续小波变换的研究进展缓慢,频域法成为当前的主要方法。在频域上,连续小波变换可看成是不同尺度且品质因数Q恒定的带通滤波器组对信号进行滤波处理,因此,设计多尺度的小波滤波器成为模拟硬件实现连续小波变换的关键技术。迄今为止,国内外学者提出了多种模拟滤波器实现连续小波变换的方法。其中,滤波器的类型主要包括连续时间滤波器[1-9]和抽样数据滤波器[10-15]。由于抽样数据滤波器的时间常数可通过调节时钟频率或元件参数比来达到精确控制,滤波器的频率特性容易改变,因此,采用抽样数据滤波器电路实现连续小波变换方法得到了研究者们的广泛关注。例如,LIN等[10]提出了基于并联结构开关电容滤波器的连续小波变换实现方法,通过调节滤波器中的时钟频率精确实现不同尺度小波函数,但开关电容电路中需要线性浮置电容,该结构与数字VLSI CMOS工艺不兼容,难于集成化。此外,随着集成工艺的发展,电源电压越来越低,直接减小电路上的最大电压摆幅,致使电压模开关电容电路的动态范围会随之减小,特别是低压高速的运算放大器设计困难。为了解决开关电容电路面临的问题,基于电流模开关电流技术的小波滤波器实现成为当前的重要研究方向。其中,胡沁春等[11]提出了基于Padé频域逼近的串联结构开关电流滤波器实现连续小波变换方法,但Padé逼近法中分子和分母多项式次数难于确定且不能保证获得的系统是稳定的。赵文山等[12]利用最小二乘法逼近时域小波函数,采用并联结构开关电流滤波器设计实现连续小波变换,但最小二乘法属于局部优化算法,使该算法收敛至最优的初始值难以选择;LI等[13-15]采用智能优化算法逼近时域小波函数,但该算法的参数设置复杂,迭代次数多,运行时间长。另外,串、并联结构小波滤波器电路较复杂,且通带灵敏度高。针对上述方法的不足,本文作者提出一种基于傅里叶级数的多环反馈开关电流小波滤波器设计新方法。利用傅里叶级数逼近法求取时域小波逼近函数,并采用开关电流双线性积分器和电流镜电路作为基本单元设计出冲激响应为小波逼近函数的多环反馈小波滤波器,通过调节滤波器的时钟频率获得不同尺度小波函数。通过仿真实验结果验证该方法的有效性。
1 小波函数的傅里叶级数逼近
傅里叶级数逼近属于一种正交函数逼近法。周期函数f(t)的傅氏级数展开式为
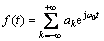 (1)
(1)
其中:ak为f(t)的傅氏级数展开的系数。由式(1)可知:f(t)为周期函数,用它无法直接逼近1个可实现的时限脉冲响应函数h(t)(如小波函数)。为了能够应用傅里叶级数逼近该类型函数,可沿时间轴重复h(t)产生1个周期为T的周期信号hT(t),且将式(1)中无限项截断成只包含2N+1项的傅氏级数展开式及频域表达式:
 (2)
(2)
为了保留hT(t)在0<t<T时的部分,将hT(t)·u(t)经过1个差分系统[16]:
 (3)
(3)
则
 (4)
(4)
式中:“*”表示卷积。由式(4)可知:该函数不是有理函数,不能直接通过电路综合实现。为了利用傅氏级数逼近算法,对被研究函数进行处理。假设h(t)为时限函数,即对于t<0和t>T,构造2个周期函数hm1(t)和hm2(t):
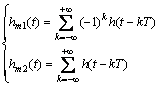 (5)
(5)
且
 (6)
(6)
根据函数hm1(t)和hm2(t)的对称性,在2T周期内将它们展开成傅里叶级数,hm1(t)只包含奇次谐波,hm2(t)只包含偶次谐波。现构造函数 和
和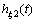 ,分别定义为
,分别定义为
 (7)
(7)
其中,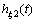 可以由
可以由 延迟T得到,在频域可表示为
延迟T得到,在频域可表示为
 (8)
(8)
将式(7)代入式(8)并整理后得
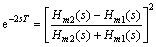 (9)
(9)
将式(7)和式(9)代入式(4)可求得H(s)为
 (10)
(10)
H(s)经拉普拉斯反变换后即可获得h(t)。
现以高斯小波函数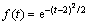 为例,采用傅里叶级数法求取其逼近函数。由于
为例,采用傅里叶级数法求取其逼近函数。由于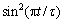 能够较好地逼近高斯函数,根据上述傅里叶级数逼近理论,可得hm1(t)和hm2(t)分别为
能够较好地逼近高斯函数,根据上述傅里叶级数逼近理论,可得hm1(t)和hm2(t)分别为
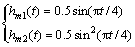 (11)
(11)
f(t),hm1(t)和hm2(t)的波形如图1所示。
将式(11)经拉普拉斯变换后代入式(10)求得尺度为1的高斯小波频域逼近函数H(s)为
 (12)
(12)
其他尺度小波逼近函数可根据拉普拉斯变换的尺度性质求得。图2所示为高斯小波函数与逼近函数的对比结果。从图2可看出:逼近函数与原函数之间的逼近效果比较理想。若需要提高逼近精度,则可增加傅里叶级数的分解次数;但随着系统传递函数中次数的增加,相应硬件电路结构变得复杂,功耗和体积也会增大。在实际应用中,通常根据精度要求选择合适的傅里叶级数分解次数。
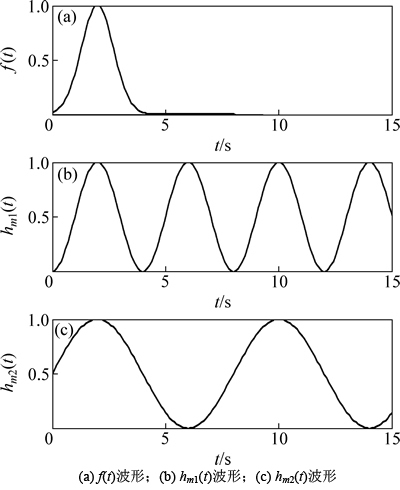
图1 f(t),hm1(t)和hm2(t)波形
Fig. 1 Waveforms of f(t), hm1(t) and hm2(t)
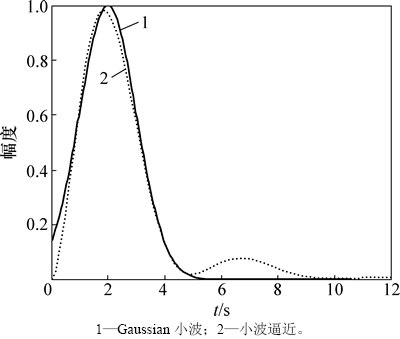
图2 高斯小波函数的傅里叶级数逼近
Fig. 2 Gaussian wavelet approximation with Fourier series
2 开关电流小波滤波器设计
通过傅里叶级数逼近法获得基本小波的逼近函数后,采用开关电流电路设计冲激响应为小波逼近函数的滤波器。常见的开关电流滤波器采用串联和并联结构实现。其中,串联结构开关电流滤波器在低频范围内有较好的频率特性,然而,这种结构存在串扰,各级滤波器的性能将决定整个滤波器的性能;并联结构滤波器在减小串扰和提高处理速度方面都优于串联结构,但该结构滤波器一般需要求和增益放大器,致使滤波器的动态范围受到限制。多环反馈结构是设计连续时间滤波器的常用方法,该方法具有设计过程简单、灵敏度低、动态范围大和通用性好的特点,因此,本文将以双输入多输出开关电流双线性积分器和单输入多输出电流镜为基本结构单元,设计实现多环反馈结构开关电流小波滤波器。
双输入多输出开关电流双线性积分器电路结构和对应的简化符号分别如图3(a)和图3(b)所示。图中 和
和 分别为积分器的同相和反相输入端电流;电流
分别为积分器的同相和反相输入端电流;电流 和
和 分别为积分器的同相和反相输出端电流。双线性开关电流积分器的z域和s域传递函数分别为:
分别为积分器的同相和反相输出端电流。双线性开关电流积分器的z域和s域传递函数分别为:
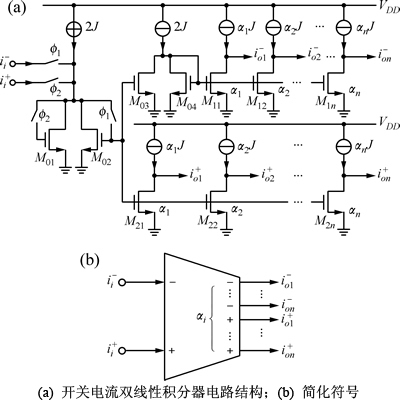
图3 双输入多输出开关电流双线性积分器及符号
Fig. 3 Bi-input-multi-output switched-current bilinear integrator and symbol
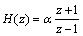 (13)
(13)
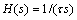 (14)
(14)
利用双线性变换(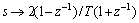 ),对比式(13)和(14)可得
),对比式(13)和(14)可得
 (15)
(15)
其中:T为采样周期;α为晶体管参数;τ为时间常数。单输入多输出电流镜电路结构和对应的简化符号分别如图4(a)和图4(b)所示,其中,k1和k2为输出增益尺度因子,可以通过调整相应NMOS晶体管宽长比获得。
考虑任意阶模拟系统的s域传递函数为
 (16)
(16)
其中: 和
和 均为实系数。分析式(16)可知它可以采用理想积分器为基本单元通过FLF结构滤波器实现。然而,为了实际实现方便,通常采用通用积分器
均为实系数。分析式(16)可知它可以采用理想积分器为基本单元通过FLF结构滤波器实现。然而,为了实际实现方便,通常采用通用积分器 替代理想积分器(1/s),因此,式(16)可以改写为
替代理想积分器(1/s),因此,式(16)可以改写为
 (17)
(17)
对比式(16)和式(17)中的分子与分母,即可求出式(17)中的各系数。将式(12)中传递函数转化式(17)的形式并进行双线性变换,然后,以开关电流双线性积分器和电流镜为基本单元设计FLF滤波器结构图如图5所示。图5中,αi,αfi和 αri(i=1,2,3)分别为开关电流双线性积分器参数、FLF结构滤波器的反馈系数和前馈系数。根据式(16)和式(17)可得出αi,αfi 和 αri的通式为:
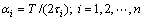 (18)
(18)

 (19)
(19)
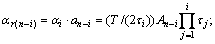
 (20)
(20)
开关电流小波滤波器电路如图6所示。图6中所有偏置电流源已省略,“①”和“②”为网络标号,同一标号表示物理上是相连的。
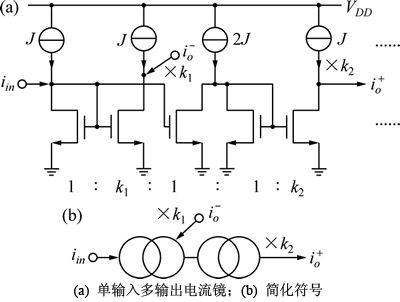
图4 单输入多输出电流镜及符号
Fig. 4 Single-input-multi-output current mirror and symbol

图5 开关电流小波滤波器结构
Fig. 5 Structure of switched-current wavelet filter

图6 开关电流小波滤波器电路
Fig. 6 Switched-current wavelet filter circuits
3 仿真与分析
为了验证文中提出的基于傅里叶级数逼近的多环反馈开关电流小波滤波设计方法的有效性, 对图6中的开关电流高斯小波滤波器电路采用ASIZ软件[17]进行仿真分析。设电路中输入电流源电流为1 A,输出电阻为1 Ω,并利用计算求得α1,α2,α3,αf0,αf1,αf2和αr0分别为0.224 6,0.224 6, 0.112 3,0.027 2,0.138 4,0.176 3和0.069 2,将这些参数设置相应晶体管宽长比,其余所有晶体管的宽长比均为1。选取时钟频率为10 kHz(对应小波滤波器尺度a为1),根据开关电流滤波器电路中膨胀系数可通过调节电路时钟频率获得的特点,调整时钟频率可获得不同尺度小波函数。例如,取时钟频率为5 kHz时滤波器可获得尺度a为2的小波函数,其他可依此类推。尺度a为1和2的高斯小波滤波器仿真结果如图7所示。对比图7与图2中的波形可看出:开关电流小波滤波器的输出结果与原函数在形态上的逼近效果比较理想。图7中波形分别在0.9 ms和1.8 ms处取得峰值0.217 04 A,与原函数归一化后的幅度基本一致。如若调整滤波器脉冲响应的增益,则可在输出端增设1个输出电流镜(如图4所示),通过调节输出电流镜的宽长比即可方便地改变输出波形的幅度,实现任意增益调整。
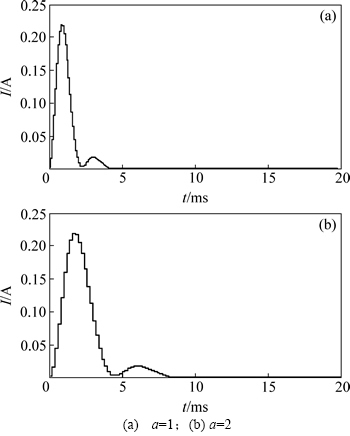
图7 开关电流小波滤波器脉冲响应
Fig. 7 Impulse responses of switched-current wavelet filter
为了检验设计的FLF结构开关电流高斯小波滤波器的低灵敏度特性,对该电路灵敏度进行分析。考虑开关电流小波滤波器电路中所有晶体管跨导存在±5%的随机误差,通过统计计算得到幅频特性误差范围,如图8所示。比较正常幅频特性曲线与误差上下限可知:所设计的滤波器电路在元件存在误差的情况下,幅频特性误差范围很小,最大增益误差为0.521 dB,验证了滤波器电路对元件误差的灵敏度低。图8中内插窗口为系统的零极点分布图,所有极点均采用z1/2的幂形式来表示,因而,对于3阶的高斯小波滤波器,窗口中给出了6个极点。从图8可看出:所有极点均位于z平面单元圆内,表明所设计的系统稳定。
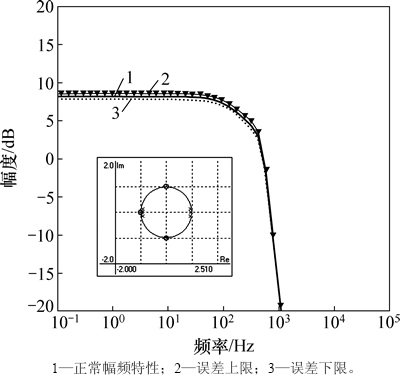
图8 开关电流小波滤波器频率响应误差范围和零极点图(a=1)
Fig. 8 Frequency responses with error margins and pole-zero plot of switched-current wavelet filter (a=1)
MOS晶体管存在非理想特性将影响开关电流电路的性能。为了检验元件非理想性对开关电流小波滤波器的影响程度,选择晶体管的输出-输入电导比误差进行研究。假设晶体管的输入电导与输出电导的比值gm/gds为1 000,电路中其他参数保持不变,小波滤波器脉冲响应的时频分布如图9(b)所示。对比图9(a)中正常情况下滤波器脉冲响应的时频分布结果可知:两者出现峰值的位置完成相同,只是非理想情况下的幅度略微减小,说明电路受该类型误差影响很小。以上仿真分析结果验证了设计出的开关电流小波滤波器具有精度高、灵敏度低、受元件非理性影响小的特点。通过调整滤波器的时钟频率即可获得不同尺度小波函数实现小波变换。

图9 正常和非理想情况下小波滤波器脉冲响应的时频分布(a=1)
Fig. 9 Time-frequency distributions of impulse responses for normal and imperfect wavelet filter (a=1)
4 结论
1) 针对现有抽样数据电路实现小波滤波器方法存在的不足,提出了基于傅里叶级数的多环反馈开关电流小波滤波器实现方法。采用傅里叶级数逼近法求取时域小波逼近函数,该方法简单且快捷,无需复杂参数调整。此外,可根据实际需求,通过增加傅里叶级数分解次数提高小波函数的逼近精度。
2) 采用多环反馈结构设计开关电流小波滤波器比串、并联结构滤波器设计更直接,不需要分解系统传递函数,且通用性强,灵敏度低,电路对晶体管的非理想性影响小。同时,该结构设计方法对其他类型抽样数据滤波器设计具有借鉴作用。
3) 利用多输出开关电流双线性积分器和多输出电流镜实现多环反馈网络中前馈和反馈系数,使电路设计变得简单,而且只需要调节相应晶体管参数即可实现新滤波器设计。
参考文献:
[1] KAREL J M H, HADDAD S A P, HISENI S, et al. Implementing wavelets in continuous-time analog circuits with dynamic range optimization[J]. IEEE Transactions on Circuits and Systems, 2012, 59(1): 2023-2032.
[2] GURROLA-NAVARRO M A, ESPINOSA-FLORES-VERDAD G. Analogue wavelet transform with single biquad stage per scale[J]. Electronics Letters, 2010, 46(9): 616-618.
[3] AGOSTINHO P R, HADDAD S A P, DE LIMA J A, et al. An ultra low power CMOS PA/V transconductor and its application to wavelet filters[J]. Analog Integrated Circuits and Signal Processing, 2008, 57(1/2): 1-14.
[4] HADDAD S A P, BAGGA B, SERDIJN W A. Log-domain wavelet bases[J]. IEEE Transactions on Circuits and Systems, 2005, 52(10): 2023-2032.
[5] CASSON A J, RODRIGUEZ-VILLEGAS E. Nanowatt multi-scale continuous wavelet transform chip[J]. Electronics Letters, 2014, 50(3): 153-154.
[6] CASSON A J, RODRIGUEZ-VILLEGAS E. A 60 pW gmC continuous wavelet transform circuit for portable EEG systems[J]. IEEE J Solid-State Circuits, 2011, 46(6): 1406-1415.
[7] ZHAO Wenshan, SUN Yichuang, HE Yigang. Minimum component high frequency Gm-C wavelet filters based on Maclaurin series and multiple loop feedback[J]. Electronics Letters, 2010, 46(1): 34-36.
[8] GURROLA-NAVARRO M A, ESPINOSA-FLORES-VERDAD G. Analogue wavelet transform with single biquad stage per scale[J]. Electronics Letters, 2010, 46(9): 616-618.
[9] GURROLA-NAVARRO M A, CARRASCO-ALVAREZ R, MEDINA-VAZQUEZ A S, et al. On-chip wavelet denoising system implemented with analogue circuits[J]. Electronics Letters, 2013, 49(9): 592-594.
[10] LIN J, KI W H, EDWARDS T, et al. Analog VLSI implementations of auditory wavelet transforms using switched-capacitor circuits[J]. IEEE Transactions on Circuits and Systems, 1994, 41(9): 572-583.
[11] 胡沁春, 何怡刚, 郭迪新, 等. 基于开关电流技术的小波变换的滤波器电路实现[J]. 物理学报, 2006, 55(2): 641-647.
HU Qinchun, HE Yigang, QIU Dixin, et al. Analog implementation of wavelet transform based on using switched-current filter circuits[J]. Acta Physica Sinica, 2006, 55(2): 641-647.
[12] 赵文山, 何怡刚. 一种改进的开关电流滤波器实现小波变换的方法[J]. 物理学报, 2009, 58(2): 843-851.
ZHAO Wenshan, HE Yigang. An improved method for implementation of wavelet transform utilizing switched-current filters[J]. Acta Physica Sinica, 2009, 58(2): 843-851.
[13] LI M, HE Y G, LONG Y. Analog VLSI implementation of wavelet transform using switched-current circuits[J]. Analog Integrated Circuits and Signal Processing, 2012, 71(2): 283-291.
[14] LI M, HE Y G. Analog complex wavelet transform using ACDE algorithm and SI filters[J]. Sensor Letters, 2011, 10(5/6): 1332-1338.
[15] LI M, HE Y G. Analogue implementation of wavelet transform using discrete time switched-current filters[C]//ZHU Min. Electrical Engineering and Control. Berlin, Germany: Springer, 2011: 677-682.
[16] 刘亚康. 时域逼近[M]. 北京: 高等教育出版社, 1993: 143.
LIU Yakang. Time-domain approximation[M]. Beijing: Higher Education Press, 1993: 143.
[17] DE QUEIROZ A C M, PINHEIRO P R M,  L P. Nodal analysis of switched-current filters[J]. IEEE Transactions on Circuits and Systems, 1993, 40(1): 10-18.
L P. Nodal analysis of switched-current filters[J]. IEEE Transactions on Circuits and Systems, 1993, 40(1): 10-18.
(编辑 陈灿华)
收稿日期:2015-09-10;修回日期:2015-11-10
基金项目(Foundation item):国家自然科学基金资助项目(61404049, 61274026);国家杰出青年科学基金资助项目(50925727);湖南省科技计划项目(2013FJ2011, 2014FJ2017);湖南省教育厅项目(14B060,10C0672) (Projects (61404049, 61274026) supported by the National Natural Science Foundation of China;Project (50925727) supported by the National Natural Science Funds of China for Distinguished Young Scholar;Projects (2013FJ2011,2014FJ2017) supported by the Science and Technology Plan Foundation of Hunan Province; Projects (14B060, 10C0672) supported by the Scientific Research Fund of Education Department of Hunan Province)
通信作者:李目,博士,副教授,从事模拟信号处理、高速低压低耗集成电路与系统、模拟电路测试与诊断和智能信息处理等研究;E-mail:limuucn@163.com