Porosity of crushed rock layer and its impact on thermal regime of Qinghai-Tibet Railway embankment
来源期刊:中南大学学报(英文版)2017年第4期
论文作者:李国玉 刘明浩 牛富俊 林战举 商允虎
文章页码:977 - 987
Key words:Qinghai-Tibet Railway; crushed rock embankment; porosity; wind-blown sand; permafrost degradation
Abstract: It has been proven that crushed rock layers used in roadbed construction in permafrost regions have a cooling effect. The main reason is the existence of large porosity of the rock layers. However, due to the strong winds, cold and high radiation conditions on the Qinghai-Tibet Plateau (QTP), both wind-blown sand and/or weathered rock debris blockage might reduce the porosity of the rock layers, resulting in weakening the cooling effect of the crushed rock layer (CRL) in the crushed rock embankment (CRE) of the Qinghai-Tibet Railway (QTR) in the permafrost regions. Such a process might warm the underlying permafrost, and further lead to potential threat to the QTR’s integrity and stability. The different porosities corresponding to the different equivalent rock diameters were measured in the laboratory using water saturation method, and an empirical exponential equation between porosity and equivalent rock diameter was proposed based on the measured experimental data and an important finding is observed in our and other experiments that the larger size crushed rock tends to lead to the larger porosity when arbitrarily packing. Numerical tests were carried out to study impacts of porosity on permafrost degradation and differential thaw depths between the sunny and shady shoulders. The results show that the decrease in porosity due to wind-blown sand or weathered rock debris clogging can worsen the permafrost degradation and lead to the asymmetric thermal regime. In the traditional embankment (without the CRL within it), the largest differential thaw depth can reach up to 3.1 m. The optimized porosity appears in a range from 34% to 42% corresponding to equivalent rock diameter from 10 to 20.5 cm. The CRE with the optimized porosities can make underlying permafrost stable and 0 °C isotherms symmetric in the coming 50 years, even under the condition that the climate warming can lead to permafrost degradation under the CRE and the traditional embankment. Some practical implications were proposed to benefit the future design, construction and maintenance of CRE in permafrost regions.
Cite this article as: LIU Ming-hao, LI Guo-yu, NIU Fu-jun, LIN Zhan-ju, SHANG Yun-hu. Porosity of crushed rock layer and its impact on thermal regime of Qinghai-Tibet Railway embankment [J]. Journal of Central South University, 2017, 24(4): 977-987. DOI: 10.1007/s11771-017-3500-2.
J. Cent. South Univ. (2017) 24: 977-987
DOI: 10.1007/s11771-017-3500-2
LIU Ming-hao(刘明浩)1, 2, LI Guo-yu(李国玉)1, NIU Fu-jun(牛富俊)1,
LIN Zhan-ju(林战举)1, SHANG Yun-hu(商允虎)1, 2
1. State Key Laboratory of Frozen Soil Engineering, Cold and Arid Regions Environmental and Engineering
Research Institute, Chinese Academy of Sciences, Lanzhou 730000, China;
2. School of Resources and Environment, University of Chinese Academy of Sciences, Beijing 100049, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract: It has been proven that crushed rock layers used in roadbed construction in permafrost regions have a cooling effect. The main reason is the existence of large porosity of the rock layers. However, due to the strong winds, cold and high radiation conditions on the Qinghai-Tibet Plateau (QTP), both wind-blown sand and/or weathered rock debris blockage might reduce the porosity of the rock layers, resulting in weakening the cooling effect of the crushed rock layer (CRL) in the crushed rock embankment (CRE) of the Qinghai-Tibet Railway (QTR) in the permafrost regions. Such a process might warm the underlying permafrost, and further lead to potential threat to the QTR’s integrity and stability. The different porosities corresponding to the different equivalent rock diameters were measured in the laboratory using water saturation method, and an empirical exponential equation between porosity and equivalent rock diameter was proposed based on the measured experimental data and an important finding is observed in our and other experiments that the larger size crushed rock tends to lead to the larger porosity when arbitrarily packing. Numerical tests were carried out to study impacts of porosity on permafrost degradation and differential thaw depths between the sunny and shady shoulders. The results show that the decrease in porosity due to wind-blown sand or weathered rock debris clogging can worsen the permafrost degradation and lead to the asymmetric thermal regime. In the traditional embankment (without the CRL within it), the largest differential thaw depth can reach up to 3.1 m. The optimized porosity appears in a range from 34% to 42% corresponding to equivalent rock diameter from 10 to 20.5 cm. The CRE with the optimized porosities can make underlying permafrost stable and 0 °C isotherms symmetric in the coming 50 years, even under the condition that the climate warming can lead to permafrost degradation under the CRE and the traditional embankment. Some practical implications were proposed to benefit the future design, construction and maintenance of CRE in permafrost regions.
Key words: Qinghai-Tibet Railway; crushed rock embankment; porosity; wind-blown sand; permafrost degradation
1 Introduction
The Chinese Qinghai-Tibet Railway (QTR) is the longest high-altitude railway in the world, which crosses the 550-km-long permafrost area on the Qinghai-Tibet Plateau (QTP) (Fig. 1). Permafrost under the QTR became warm and the thaw depth increases due to construction distribution and climate warming [1-4]. Permafrost degradation and active layer thickening reduce its mechanical strength and load-bearing capacity, and might seriously affect stability of the QTR embankment [5-9]. Some proactive measures for cooling the railway subgrade and protecting the underlying permafrost from thawing have been successively applied in the QTR project, especially in warm and ice-rich permafrost areas [10-13]. The crushed-rock embankment (CRE) is one kind of the efficient structural configurations in protecting the underlying permafrost due to its “thermal semi-conductor” effect or cooling effect [8, 14-17]. The crushed rock layer (CRL) can always be put at the bottom of an embankment or on the side slopes. In winter, natural convection (buoyancy- induced motion) of the pore air in the CRL occurs due to lower ambient air temperature than ground temperature at the bottom of the CRL. It generally has stronger heat exchange than conductive heat transfer. During the summer, the CRL is heated from the upper boundary and no convection occurs since the air density gradient is stable [13].
So far, much research has been carried out to study the cooling mechanisms and cooling effect, design optimization of the CRL in the QTR through field observation, laboratory model tests at different scales and a variety of numerical simulation tests [3, 8, 13, 18-21].

Fig. 1 Qinghai-Tibet Railway route and some sand damage locations
Recently, some researchers reported that the wind- blown, shifting sand buried the railway at some sites along the QTR [22, 23]. The windblown sand particles mostly affect the external portions of the crushed rock layer. As shown in Fig. 2, the CRL in some railway embankments has gradually been filled and clogged by the sands, which could cause reduction in porosity of the CRL and weaken its cooling effect, and also weathering of the crushed rocks might influence the CRL in the same way. So, the long-term adaptability and cooling effect of the CRE has become a concern for the QTR under adverse impacts of wind-blown sand clogging and rock weathering in permafrost areas.
However, though the porosity measurement was studied by HE et al [24], the impact of permeability or porosity changes on air convection of the highly porous CRL and on the cooling effect has been less studied. Porosity and permeability of CRL are two of the primary parameters that control the fluid movement in void space and physical characteristics of porous materials such as the effective thermal conductivity. Porosity is defined as the ratio of volume of the void space to the bulk volume of a porous medium. Permeability or intrinsic permeability expresses the ease with which a fluid is transported through a porous matrix. Therefore, it depends only on properties of the solid matrix and controls fluid convection in pore space. Various formulae are described in the literature relating permeability to the various properties of the solid matrix. Some of these formulae are empirical. For example, FAIR and HATCH [25] developed an empirical formula from dimensional considerations and verified experimentally.

Fig. 2 Wind-blown sand clogging and rock-weathering in QTR embankment:
With the “thermal semi-conductor” effect caused by its high porosity, CRL was the most applied embankment structure in the QTR construction in sensitive permafrost areas. Change in porosity is of significant importance due to its influence on the cooling effect. Therefore, there is an urgent need for further understanding and assessing the variation of cooling effect affected by the sand blocking and rock weathering. The objectives of this work are: 1) to measure the different porosities in the laboratory corresponding to the different rock diameters, 2) to model the cooling effects using the numerical method when porosity of CRL in the embankment varied due to blocking and clogging of wind-blown sand or rock weathering, and 3) to provide possible measures to keep the porosity of the CRL, to guarantee its cooling effect and protect the long-term stability of the QTR roadbed in the permafrost regions.
2 Porosity measurement
Porosity is an important parameter for calculating the permeability of porous media using the semiempirical equation [26]. So far, few studies have focused on measuring the porosity of poorly-graded media with large particle diameters (larger than 10 cm) such as crushed rock. HE et al [24] conducted some laboratory experiments to measure the porosity of poorly-graded crushed rock. In order to accumulate and enrich the experimental data of porosity of CRL and facilitate the following numerical simulations, the porosity of four other crushed rock samples was herein determined by the water saturation method. The average particle diameters of the samples were equal to 20.5, 17.5, 12 and 10 cm, respectively. The measured crushed rocks were collected and hauled to the laboratory from the field along the QTR. The testing procedure was described as follows. Firstly, the equivalent rock diameter was measured. The equivalent rock diameter is really the volume equivalent spherical diameter of an irregularly-shaped rock, which can be obtained by equating the volume of an irregularly-shaped rock with that of the regularly-shaped sphere with a diameter. For the rocks with a certain equivalent diameter, 10 of them were typically selected to be immersed in a fully water-filled container. The volume of the spilled water is the volume of a rock, by which the equivalent rock diameter was determined [27]. Secondly, porosity of crushed rock layer was measured. Considering the practical construction of the CRE in field, the crushed rocks with an equivalent diameter were arbitrarily placed in a large steel box (length'width'.0 m'1.2 m'0.4 m) (Fig. 3(a)). Determine the total volume Vt of porous media through calculating the inner volume of steel box; Secondly, pump water into the steel box and saturate the CRL (Fig. 3(b)). Determine the pumped water volume Vw; Finally, drain the water and remove the crushed rock out of steel box. Porosity n can be obtained as follows:
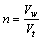 (1)
(1)
Similarly, the other porosities were measured through the same procedure. All measured porosities are listed in Table 1 and analyzed. Meantime, the porosity of 47.5% corresponding to rock diameter of 25 cm is also added in Table 1 [24]. These measured data are plotted in Fig. 4 and denoted as empty circles.
Considering the difficulty of repeated porosity testing, only one test of porosity has been done for a given crushed rock diameter in this experiment.
Note that the porosity of the crushed rock increases with increasing rock diameter in the measured diameter range, which is not like the variation for the uniform spheres [26]. An exponential curve describing the relationship between porosity of crushed rock layer and equivalent diameter can be gained by fitting the measured data, and its empirical equation reads as follows:
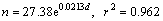 (2)
(2)
where n, d and r2 represent porosity, equivalent rock diameters and coefficient of determination, respectively. This empirical equation can be used to relatively accurately predict the unknown porosity of non-uniform porous media such as crushed rock corresponding to some particle diameters.

Fig. 3 Measuring porosity of crushed rock layer using water saturation method:
Table 1 Types of magmatic sulfide deposits in China
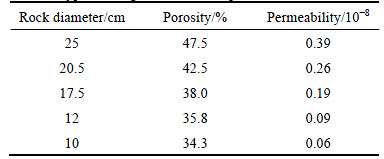
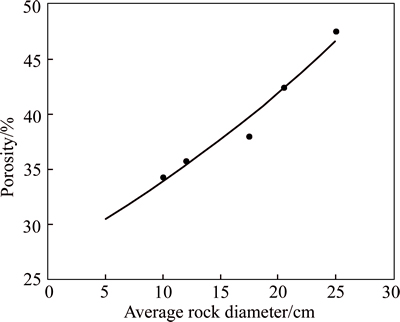
Fig. 4 Correlation between porosity of CRL and equivalent diameter
3 Modeling conditions
The CRL in the embankment is highly porous media. The pore air can flow in a form of natural convection due to density gradient when the upper air temperature is lower than that at the lower portion. This convective heat transfer can be described by the continuity, momentum, energy equations [16, 28, 29]. The numerical computational domain for the CRE model (Fig. 5) was established according to the typical cross section of the QTR [16, 30]. In portions other than the CRL, heat transfer is dominated by conduction. The traditional differential equations of heat conduction can be used to describe this heat transfer process [31]. In the CRL zone, the continuity, momentum, energy and state equations were established [17, 29], and heat radiation within it is not included. Numerical modelling results were verified with the laboratory results, and it was shown that the two results were in good agreement [32]. Similar works by LAI et al [33, 34] also showed that the modelling method can be employed readily here to simulate the influence of porosity of the CRL on its cooling effects.
The CRE has 1: 1.5 side slopes, a width of 7.6 m at the crest of the driving surface and a height of 3.7 m including a 1.2-m-thick crushed rock layer at its bottom. For the traditional embankment model (without the CRL within it), there is no CRL within it. The numerical model has a 30-m-wide horizontal extension from right and left slope toes and this aims to eliminate the boundary effect. In vertical direction, the model also hasa 30-m-deep extension including 0.5-m-thick sandy soil layer with gravels, 1.5-m-thick sandy soil layer, 6-m- thick silty clay layer belonging to the ice-rich permafrost and 22-m-thick strongly-weathered mudstone.
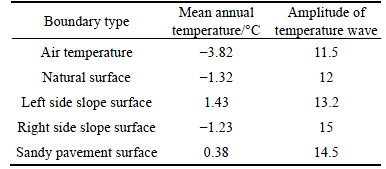
The effect of climate warming on the thermal regime was taken into account in the simulations. The air temperature is assumed to warm by 2.6 °C over the next 50 years on the Qinghai-Tibet Plateau [35]. The boundary conditions are determined according to the theory of adherent layer [36] and related literature [33, 37] as shown in Eq. (3) and Table 2. The various boundary temperatures can be expressed as the following general form:
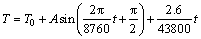 (3)
(3)
where T represents air temperature or various surface temperatures; T0 is the mean annual temperature; A is the amplitude of temperature wave and t is the time.
It is noted that the left side slope is the east-facing slope along the QTR, which gets more solar radiation and has higher surface temperature, also called sunny slope. The right side slope is the west-facing slope, which gets less sunlight and has lower surface temperature relative to the left side slope, also called shady slope.
According to the monitored ground temperatures of deep permafrost underlying the QTR, the geothermal gradient varied from 0.025 to 0.05 °C/m, most of which fluctuated around 0.04 °C/m [38]. Therefore, the geothermal gradient is set as 0.04 °C/m in this work. The heat flux can be obtained through multiplying the geothermal gradient with the thermal conductivity of permafrost layer. On both sides of the model, the adiabatic boundary conditions are set, where the heat flux is zero. The initial air velocity in porous medium is set as 0 m/s. The boundary conditions of porous zone are impermeable.
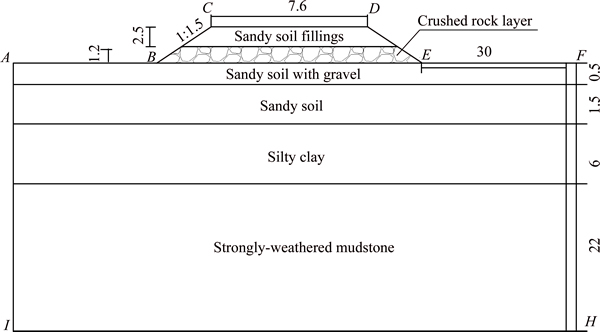
Fig. 5 Numerical computational domain and ground stratigraphy (Unit: m)
Table 2 Parameters of temperature boundary conditions
The thermal parameters are shown in Table 3 [16, 39]. Thermal properties of crushed rock keep constant. However, the overall thermal properties of crushed rock layer change with porosity and rock diameter. The permeability of crushed rock layer with different porosities and diameters can be calculated with the Fair and Hatch formula [26]:
 (4)
(4)
where k and d are the intrinsic permeability and average particle size of crushed rock layer; N is the percentage of crushed rock held between both adjacent size limits of the sieve plate; dm is the geometric mean size between both adjacent size limits of the sieve plate and a is the particle shape parameter in the crushed rock matrix, which here is set as 7.7 for angular particles [26]. The permeabilities were calculated from this formula and are shown in Table 1.
The porosity significantly affects the thermal conductivity and heat capacity of porous medium. Generally, the overall thermal conductivity of a porous medium depends on the geometry of the medium. If the heat conduction in the solid and fluid phases in parallel, the overall thermal conductivity lA is the weighted arithmetic mean of the conductivities, i.e., the thermal conductivity for the solid phase ls and the thermal conductivity for the fluid phase lf. The relationship with porosity is shown in the following equation:
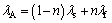 (5)
(5)
If the structure and orientation of the porous medium is such that the heat conduction takes place in series, with all of the heat flux passing through both solid and fluid, then the overall conductivity lH is the weighted harmonic mean of ls and lf:
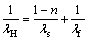 (6)
(6)
For practical purposes, a rough and ready estimate for the actual overall conductivity lm is provided by lG, the weighted geometric mean of ls and lf as
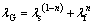 (7)
(7)
The effect of porosity on the heat capacity of the porous medium (effective heat capacity) ce can be described according to the following equation [26]:
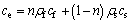 (8)
(8)
The initial temperature underneath the embankment can be gained through a long-term transient solution applying Eq. (3) on the original ground surface without considering effects of climatic warming. Here the thermal regime of the embankment on 15 July 50 years later is chosen to act as the initial one. The original ground temperature of the embankment is set as 10 °C.
4 Numerical results
As numerical simulations modeled, it is assumed that the windblown particles uniformly fill the crushed rock layer for simplifying the following numerical modelling. It is also assumed that the freeze-thaw weathering uniformly leads to decrease in porosity of crushed rock layer. If the actual processes were considered, it is hard to model them.
Four CRE models with four different porosities (Table 1) corresponding to different rock diameters or shifting sand clogging rates or rock weathering rate were used to model their cooling effect on the underlying permafrost. One traditional embankment model was also used to compare their cooling effectiveness. The thermal regimes on the 15th October, on which the thaw front almost reaches its maximum depth, 5 and 50 years after construction are chosen to study variation in thaw depth, as shown in Figs. 6 and 7.
Table 3 Thermal parameters of various materials

Figure 6 shows temperature profiles of different embankment models on the 15th October 5 years after its construction. Figure 6(a) demonstrates thermal regime of traditional embankment. Note that there is an obviously asymmetric distribution of the thermal regimes within it due to the different solar radiations on the right and left slopes. The thaw front under the left shoulder of embankment is 1.27 m deep beneath the original ground surface. However, the thaw depth under the right shoulder is 0.54 m high above the original ground surface. The difference in thaw depth between them reaches up to 1.81 m. Permafrost temperatures at depths of 4 m to 10 m varied from -0.5 °C to -1 °C. In this temperature range, permafrost is more vulnerable to potential climate warming and warming effect of construction disturbance.
Figures 6(b)-(e) demonstrate temperature profiles of CRE models with porosities of 34%, 38%, 42% and 47%, respectively. All of 0 °C isotherms keep symmetric and the -1.5 isotherms are non-symmetric, which is the result of the asymmetric thermal boundary conditions. Thaw depths under the left and right shoulders of four CREs vary from 0.20 m to 0.25 m. There is little difference in thaw depth in these cases. Deep permafrost temperature all remain about -1.5 °C beneath these embankments, at which temperature permafrost is more stable in thermal stability as a structure supporter. Similarly, more attention should be paid to slope stability due to the higher ground temperature (-1 to -0.5°C) of ice-rich permafrost underneath the toes of the embankment.
Figure 7 shows temperature profiles of different embankment models on the 15th October 50 years after their construction. Figure 7(a) shows the thermal regime of traditional embankment. Note that there is still an obviously asymmetric temperature distribution, especially within the embankment and near the permafrost table. Thaw depths under left and right shoulder of embankment are 3.24 cm and 0.14 cm under ground surface, respectively. The difference in thaw depth between them reaches up to 3.10 m, which gets larger with time relative to 1.81 m in the 5th year. Deep permafrost temperatures vary between 0 °C and -0.25 °C, which warm by 0.5 °C and 0.75 °C compared with those in the 5th year. Permafrost at this temperature is most unstable in thermal stability. It needs to be protected by installing some structures to cool it and slow its degradation.
Figures 7(b)-(d) demonstrate temperature profiles of CRE models with porosities of 34%, 38%, and 42%, respectively. Three temperature profiles remain symmetric. All of thaw depths under the left and right shoulders of CREs with these three porosities are basically equal, about 0.28 m. Deep permafrost temperature beneath these three embankments is about -0.5 °C, which is warmer by 1 °C than that in the fifth year. The ground temperatures of the silty clay layer in these figures are between 0 °C and -0.5 °C which are vulnerable to thaw. However, this temperature of underlying permafrost is a little bit cooler than that beneath the traditional embankment in the 50th year. It suggests that the CRL play a cooling role in the underlying permafrost. Permafrost at above -0.5 °C is most vulnerable.
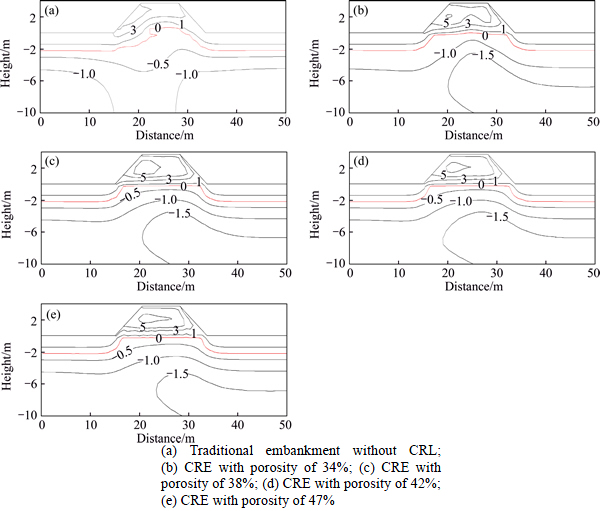
Fig. 6 Thermal regime of CRE with different porosities on 15 October after 5 years (in °C):

Fig. 7 Thermal regime of CRE with different porosities on 15 October after 50 years (in °C):
Figure 7(e) shows the temperature profile of CRE with a porosity of 47%. Note that the thermal regime remains slightly asymmetric. Thaw depths under left and right shoulder of embankment are 0.75 cm and 0.28 cm respectively, which are larger than ones in Figs. 7(b)-(d). Additionally, deep permafrost temperature becomes warmer, and reaches about -0.35 °C compared with the permafrost temperature of -0.5 °C in Figs. 7(b)-(d). This proves that there is an optimized rang of porosity of CRL for its cooling effect.
In order to study the permafrost degradation process and different cooling effects of the CREs and the traditional embankment, ground temperatures at the depth of 8 m under the ground surface beneath the left and right shoulders were monitored with time. Here the period through 30 to 40 years was chosen to investigate the typical warming process of permafrost (Fig. 8). It canbe observed that the 8 m-deep ground temperature under left shoulder is higher than that under the right shoulder due to the differential solar radiation on the left and right slopes. The traditional embankment shows a higher permafrost temperature than other CREs. In addition, the CRE with the porosity of 42% have the best cooling effect as demonstrated in Figs. 6 and 7, in other words, the optimum porosity of CRL for the best cooling effect is as much as 42% under above given conditions.
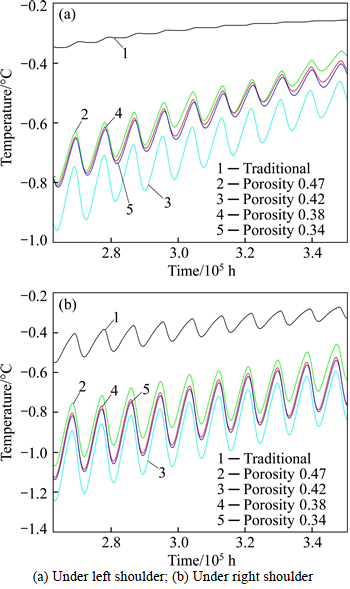
Fig. 8 Variations in 8-m-deep ground temperatures with time through the 30th to 40th year underneath various embankments:
5 Discussions
In this work, authors used the water saturation method to measure porosity of crushed rock (highly porous and permeable media). The measured diameter range of rock varied from 10 cm to 20.5 cm. HE et al [24] measured porosities of crushed rock with three diameters of 10, 15 and 25 cm. Based on these measured porosity data, an empirical equation in exponential form was built which can be used to predict other porosity of highly porous media with a diameter ranging from 10 cm to 25 cm. However, the predicted porosity of crushed rock outside this diameter range needs further calibration experimentally because measuring of porosity was affected by many factors such as the arranging manner of crushed rocks, dimension of testing box, shape and type of crushed rock and testing method. In the cases of spheres of equal size, the porosity is independent of the diameter of the spheres. However, the crushed rock layer, as a porous medium, is not a uniform medium (non- uniform spheres) because of its irregularity. Except for the particle diameter, the factors affecting its porosity of porous medium also include the packing of particles, their shape and size distribution [26]. In the practical experiments testing the porosities of the crushed rock layers with different average particle diameters, it is impossible to keep the same packing and the same shape of crushed rocks every time. So, the actual porosities are variable with average particle diameter. An important finding is observed in our and other experiments including the experimental results from HE et al [24] that larger particle diameter tends to lead to the larger porosity when arbitrarily packing the crushed rocks. The possible reason is that the crushed rocks with larger diameter are easy to create a larger void space when they are placed arbitrarily, which leads to a larger porosity. This means porosity of crushed rock layer has close relationship with diameter, due to the arbitrary placement. The finding is significant for the actual engineering construction such as selecting the larger diameter and well-sorted rocks for larger porosity and better cooling effect in cold engineering.
Numerical results show that the traditional embankment has higher permafrost temperature and asymmetric thermal regime relative to the CREs. Deep permafrost temperature is about -0.37 °C after 50 years. The traditional embankment overlying massive ground ice needs some mitigative measures to protect the underlying permafrost from thawing due to potential climate warming and construction disturbance to the ground surface. The CREs have better cooling effect relative to the traditional embankment and can adjust and improve their asymmetric thermal regimes. Nevertheless, the CRL in CRE has an optimized range of porosity for a better cooling effect, which varies from 34% to 42% from above research results. If porosity of CRL goes outside this range, its cooling effect will be considerably weakened, and the thermal regime of CRE also keeps slightly asymmetric. For instance, the deep permafrost temperatures after 50 years under the CREs with porosity of 47% rise to -0.35 °C, showing that the cooling effect of the highest porosity is less than those of smaller ones. Previous experimental and numerical results have also proved this fact, and their optimized or rational rock diameters are very close to that in this study [40-42]. However, minimal study or explanation on why this happens has been carried out in the literatures so far because of the complication of the process of heat transfer in the CRL. In general, heat is transported in three modes: conduction, convection and radiation. In a porous medium whose void space is filled with a moving fluid, the three basic modes of heat transfer may manifest themselves in the six ways [43]. Not all of these modes or ways of heat transfer have equal significance in an actual case of flow through a porous medium. Energy transport by radiation is always not taken into account. For the crushed rock layers with different rock diameters, the modes or ways of heat transfer may change with the changing rock diameters, which leads to change in contact between particles and specific surface. The cooling effectiveness of the crushed rock layer is dependent on thickness, height, permeability, contact between rocks, specific surface, arranging manner and pore size. XU et al [44] found that specific surface and pore size played an important role in heat exchange between crushed rocks and pore air. Therefore, for the crushed rock with smaller diameter (smaller than 20.5 cm in this study), permeability predominated the heat exchange between crushed rocks and pore air, namely, the larger the permeability, the better the cooling effect. While for the crushed rocks with the larger diameter (larger than 20.5 cm in this study), the remarkably decreased specific surface might replace the permeability and then predominate the heat exchange. So, the cooling effect of crushed rock layer weakens with increasing diameter (greater than 20.5 cm) though its permeability increases because the specific surface of porous materials significantly decreases with increasing diameter. In other words, the heat transfer by conduction between particles in winter can be significantly decreased, due to the decreasing of specific surface of crushed rocks. Thus, the overall cooling effect of a crushed rock layer is weakened. This explains why the biggest diameter of crushed rock layer with higher permeability shows poorer cooling effects than those smaller ones. Even so, the above explanation needs further verification in laboratory and field experiments. The CRE with an optimized porosity for a better cooling effect can ensure the thermal stability of underlying permafrost subject to climate warming in its life time, thus the optimized rock diameter ranging from 10 cm to 20.5 cm corresponding to the optimized porosity range can be gained and recommended for construction of CRE according to the established empirical equation between them.
In Ref. [5], it is shown that asymmetry of thermal regime of CRE is one of the reasons causing the longitudinal cracks on the driving surface in permafrost regions [5]. For the permafrost embankment stability, we should not only keep the underlying permafrost frozen, but also leave the thermal regime symmetric, which can reduce the differential settlement of embankments.
Some practical implications can be obtained from the above research. Firstly, there is an urgent need to prevent the wind-blown, shifting sand from entering and clogging the CRL in the CRE of the QTR at some sites. The measures to mitigate clogging of the shifting sand are suggested such as placing geotextile or shading boards on the top surface of CRL [16], and uncovering the CRL on the slopes and removing the weathered rock debris and replacing the larger ones with the optimized diameter. Secondly, the optimized rock diameter range exists for better cooling effect of the crushed rock layer which imply that the rock diameter should be carefully determined according to this and previous studies when the crushed rock embankment is adopted to cool the underlying permafrost. Thirdly, researchers find that long-term freeze-thaw weathering promotes disintegration of rock and releases rock debris in cold regions [45, 46]. The weathered rock debris might block the void space of the CRL of the CRE in the QTR and reduce its porosity. This implies that the harder rock should be selected as the raw material of crushed rocks rather than the strongly weathered sandstone or conglomerate and shale with lower strength.
Concerning the asymmetric thermal regime of QTR embankment in permafrost regions, some adjusting measures can be recommended such as placing the thicker crushed rock on sunny slope [21], installing shading boards or thermosyphons on sunny slope, and placing longitudinal air-ventilated ducts.
On the basis of above studies, further research is proposed for improvement of engineering design and construction of the CRE as follows. 1) Generally, testing of parameters needs some repeated experiments for accurate testing results and repeatability. Here, we did not do repeated experiments because testing of porosity of CRL is significantly dependent on the arrangement of the crushed rocks. In the future, the related experimental works should be done in the larger testing box for minimizing the boundary effect on porosity; 2) Lots of studies found that there is a optimized rock diameter range for a better cooling effect of CRL. Why and how this happens needs to be further studied and verified theoretically and experimentally. 3) The other measures to mitigate clogging of shifting sand need to be developed and their engineering effect need to be verified in the field and laboratory experiments.
6 Conclusions
1) Porosities of highly porous, poorly graded crushed rock being used in the CRE along the QTR were measured in laboratory using water saturation method. An empirical exponential equation between porosity and equivalent rock diameter was proposed based on the measured experimental data, which can be used to predict the unknown porosity of highly porous media with other diameters.
2) The porosity of the CRL decreases if it is clogged by wind-blown sand or weathered rock debris, which leads to faster permafrost degradation and the larger differential thaw depth between the left and right shoulders. Such problems might seriously affect the integrity and stability of the QTR embankment. In the traditional embankment, the largest differential thaw depth can reach as much as 3.1 m.
3) The CRE has better cooling effect relative to the traditional embankment and can adjust the asymmetric thermal regime. However, the CRL has an optimized porosity range for the better cooling effect, which varies from 34% to 42%. If porosity of CRL is lower than 34% possibly due to wind-blown sand or weathered rock debris clogging, the thaw depth under the CRE will significantly increase. In order to ensure the cooling effect of CRL in the QTR, some mitigative measures should be adopted such as placing geotextile or shading boards on the surface of the crushed rock layer for stopping sand entering the CRL, selecting harder and larger rock as raw materials for reducing weathering.
4) Climate warming on the QTP can significantly lead to permafrost degradation under the traditional embankment along the QTR. However, the CRE with the optimized porosities of the CRL can make the underlying permafrost stable in the coming 50 years, in which the permafrost table goes up and thermal regime is symmetric.
References
[1] CHENG Guo-dong. Influence of local factors on permafrost occurrence and their implications for Qinghai-Xizang Railway design [J]. Science in China: Series D, 2004, 47(8): 704-709.
[2] WU Qing-bai, CHENG Guo-dong, MA Wei. Impact of permafrost change on the Qinghai-Tibet Railroad engineering [J]. Science in China: Series D, 2004, 47(suppl 1): 122-130.
[3] WU Qing-bai, CHENG Hong-bin, JIANG Guan-li, MA Wei, LIU Yong-zhi. Cooling mechanism of embankment with block stone interlayer in Qinghai-Tibet railway [J]. Science in China: Series E, 2007, 50(3): 319-328.
[4] MA Wei, MU Yan-hu, WU Qing-bai, SUN Zhi-zhong, LIU Yong-zhi. Characteristics and mechanisms of embankment deformation along the Qinghai-Tibet Railway in permafrost regions [J]. Cold Regions Science and Technology, 2011, 67(3): 178-186.
[5] LAI Yuan-ming, ZHANG Shu-juan, ZHANG Lu-xin, XIAO Jian-zhang. Adjusting temperature distribution under the south and north slopes of embankment in permafrost regions by the ripped rock revetment [J]. Cold Regions Science and Technology, 2004, 39 (1): 67-79.
[6] JIN Hui-jun, ZHAO Lin, WANG Shao-ling, RUI Jin. Thermal regimes and degradation modes of permafrost along the Qinghai- Tibet Highway [J]. Science in China: Series D, 2006, 49(11): 1170-1183.
[7] LI Guo-yu, LI Ning, QUAN Xiao-juan. The temperature features for different ventilated-duct embankments with adjustable shutters in the Qinghai-Tibet railway [J]. Cold Regions Science and Technology, 2006, 44(2): 99-110.
[8] LI Guo-yu, MU Yan-hu, ZHANG Xia. Thermal characteristics of the embankment with crushed rock side slope to mitigate thaw settlement hazards of the Qinghai-Tibet Railway [J]. Acta Geologica Sinica: English Edition, 2009, 83(5): 1000–1007.
[9] PENG Hui, MA Wei, MU Yan-hu, JIN Long. Impact of permafrost degradation on embankment deformation of Qinghai-Tibet Highway in permafrost regions [J]. Journal of Central South University, 2015, 22(3): 1079-1086.
[10] YU Qi-hao, CHENG Guo-dong, NIU Fu-jun. The application of auto-temperature-controlled ventilation embankment in Qinghai- Tibet railway [J]. Science in China: Series D, 2004, 47(suppl 1): 168–176.
[11] NIU Fu-jun, XU Jia, LIN Zhan-ju, WU Qing-bai, CHENG Guo-dong. Permafrost characteristics of the Qinghai-Tibet Plateau and methods of roadbed construction of railway [J]. Acta Geologica Sinica: English Edition, 2010, 82(5): 949-958.
[12] NIU Fu-jun, CHENG Gguo-dong, YU Qi-hao. Ground-temperature controlling effects of duct-ventilated railway embankment in permafrost regions [J]. Science in China: Series D, 2004, 47(suppl 1): 152-160.
[13] CHENG Guo-dong, LAI Yuan-ming, SUN Zhi-zhong. The ‘Thermal semi-conductor’ effect of crushed rock [J]. Permafrost and Periglacial Processes, 2007, 18(2): 151-160.
[14] LAI Yuan-ming, ZHANG Ming-yi, LIU Zhi-qiang, YU Wen-bing. Numerical analysis for cooling effect of open boundary ripped-rock embankment on Qinghai-Tibetan railway [J]. Science in China: Series D, 2006, 49(7): 764-772.
[15] LAI Yuan-ming, MA Wei, ZHANG Ming-yi, YU Wen-bing, GAO Zhi-hua. Experimental investigation on influence of boundary conditions on cooling effect and mechanism of crushed-rock layers [J]. Cold Regions Science and Technology, 2006, 45(2): 114-121.
[16] LI Guo-yu, LI Ning, MA Wei. Cooling effects and mechanisms of crushed rock protective slopes combined with shading board on embankment in warm permafrost regions [J]. Rock and Soil Mechanics, 2010, 31(1): 165-173. (in Chinese)
[17] LI Guo-yu, LI Ning, KANG Jia-mei, NIU Fu-ju, YU Wen-bing, SHI Lei, BI Gui-quan. Study on design optimization of a crushed stone layer with shading board placed on a railway embankment on warm permafrost [J]. Cold Regions Science and Technology, 2008, 54(1): 36-43.
[18] GOERING D J, KUMAR P. Winter-time convection in open-graded embankments [J]. Cold Regions Science and Technology, 1996, 24: 57-74.
[19] LAI Yuan-ming, ZHANG Lu-xin, ZHANG Shu-juan, MI Long. Cooling effect of ripped-stone embankments on Qing-Tibet railway under climatic warming [J]. Chinese Science Bulletin, 2003, 48(6): 598-604.
[20] ZHANG Ming-yi, LAI Yuan-ming, YU Wen-bing, HUANG Zhi-jun. Experimental study on influence of particle size on cooling effect of crushed-rock layer under closed and open tops [J]. Cold Regions Science and Technology, 2007, 48(3): 232-238.
[21] MA Wei, ZHANG Lu-xin, WU Qing-bai. Control of asymmetrical subgrade temperature with crushed-rock embankments along the permafrost region of the Qinghai-Tibet Railway [C]// Proceedings of the 9th International Conference on Permafrost. Fairbanks: University of Alaska Fairbanks, 2008: 1099-1104.
[22] ZHANG Ke-cun, QU Jian-jun, LIAO Kong-tai, NIU Qing-he, HAN Qing-jie. Damage by wind-blown sand and its control along Qinghai- Tibet Railway in China [J]. Aeolian Research, 2010, 1(3): 143-146.
[23] ZHANG Ke-cun, QU Jian-jun, HAN Qing-jie, AN Zhi-shan. Wind energy environments and aeolian sand characteristics along the Qinghai–Tibet Railway, China [J]. Sedimentary Geology, 2012, 273-274(6): 91-96.
[24] HE Ping, CHENG Guo-dong, MA Wei, WU Qing-bai. Research on ventilation properties of block stones layer [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(6): 789-792. (in Chinese)
[25] FAIR G M, HATCH L P. Fundamental factors governing the streamline flow of water through sand [J]. Journal, 1933, 25(11): 1551-1565.
[26] BEAR J. Dynamics of fluids in porous media [M]. Amsterdam: Elsevier, 1972.
[27] JENNINGS B R, PARSLOW K. Particle size measurement: the equivalent spherical diameter [J]. Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences, 1988, 419(1856): 137-149.
[28] NIELD D A, BEJAN A. Convection in porous media [M]. Berlin: Springer, 1992.
[29] TAO Wen-quan. Numerical heat transfer [M]. 2nd ed. Xi’an: Xi’an Jiaotong University Press, 2011. (in Chinese)
[30] ZHENG Bo. Study on mechanical properties of warm and ice-rich frozen soil and roadbed deformation in permafrost regions [D]. Beijing: Graduate School of the Chinese Academy of Sciences, 2007. (in Chinese)
[31] TAYLOR G S, LUTHIN J N. A model for coupled heat and moisture transfer during soil freezing [J]. Canadian Geotechnical Journal, 1978, 15: 548-555.
[32] LI Guo-yu, LI Ning, MA Wei. Mathematic models and numerical solutions of the heat transfer for the embankment with crushed stone layer in permafrost regions [C]// Proceedings of the 8th International Symposium on Permafrost Engineering. Lanzhou: Lanzhou University Press, 2009: 242-249.
[33] LAI Yuan-ming, ZHANG Lu-xin, ZHANG Shu-juan, MI Long. Cooling effect of ripped-stone embankments on Qing-Tibet railway under climatic warming [J]. Chinese Science Bulletin, 2003, 48(6): 598-604.
[34] LAI Yuan-ming, ZHANG Ming-yi, LIU Zhi-qiang, YU Wen-bing. Numerical analysis for cooling effect of open boundary ripped-rock embankment on Qinghai-Tibetan railway [J]. Science in China Series D: Earth Sciences, 2006, 49(7): 764-772.
[35] QIN Da-he. Assessment on environment in west China [M]. Beijing: Science Press, 2002. (in Chinese)
[36] WU Zi-wang, CHENG Guo-dong, LIU Yong-zhi. Roadbed engineering in permafrost region [M]. Lanzhou: Lanzhou University Press, 1998. (in Chinese)
[37] CHOU Ya-ling. Study on shady-sunny effect and the forming mechanism of the longitudinal embankment crack in permafrost [D]. Beijing: Graduate School of the Chinese Academy of Sciences, 2007. (in Chinese)
[38] ZHOU You-wu, GUO Dong-xin, QIU Guo-qing, CHENG Guo-dong, LI Shu-xun. Geocryology in China [M]. Beijing: Science Press, 2000. (in Chinese)
[39] XU Xue-zu, WANG Jia-deng, ZHANG Li-xin. Frozen soil physics [M]. Beijing: Science Press, 2001. (in Chinese)
[40] LAI Yuan-ming, ZHANG Ming-yi, YU Wen-bing, LI Shuang-yang. Laboratory study of particle size for optimal cooling effect of closed crushed-rock layers [J]. Journal of Glaciology and Geocryology, 2006, 28(5): 755-759. (in Chinese)
[41] ZHANG Ming-yi, LAI Yuan-ming, LI Shuang-yang, ZHANG Shu-juan. Laboratory investigation on cooling effect of sloped crushed-rock revetment in permafrost regions [J]. Cold Regions Science and Technology, 2006, 46(1): 27-35.
[42] BIAN Xiao-lin, HE Ping, WU Qing-bai, SHI Ye-hui. Experimental study on the influence of the particle diameter on the natural convection characteristics of the block stone layer [J]. China Railway Science, 2011, 32(1): 1-6. (in Chinese)
[43] HOLMANJ P. Heat transfer [M]. 6th ed. Singapore: McGraw-Hill Book Company, 1986.
[44] XU Xue-zu, SUN Bin-xian, LIU Qi, WANG Shuang-jie, ZHANG Jin-zhao. Laboratory experiment on the influence of paving location and diameter on the cooling effect of ballast embankment [J]. Chinese Journal of Geotechnical Engineering, 2005, 27(3): 254-257. (in Chinese)
[45] MATSUOKA N, MURTON J. Frost weathering: recent advances and future directions [J]. Permafrost and Periglacial Processes, 2008, 19: 195-210.
[46] NIU Fu-jun, LIU Hua, LIN Zhan-ju, LU Jia-hao. Physical changes of five types of rock in the Qinghai-Tibet Plateau under freeze-thaw cycles [C]// Proceedings of the 9th International Symposium on Permafrost Engineering. Mirnyy: Melnikov Permafrost Institute, Russia Academy of Sciences, 2011: 46-51.
(Edited by YANG Hua)
Cite this article as: LIU Ming-hao, LI Guo-yu, NIU Fu-jun, LIN Zhan-ju, SHANG Yun-hu. Porosity of crushed rock layer and its impact on thermal regime of Qinghai-Tibet Railway embankment [J]. Journal of Central South University, 2017, 24(4): 977-987. DOI: 10.1007/s11771-017-3500-2.
Foundation item: Project(2012CB026101) supported by the National Key Basic Research Program of China (973 Program); Project(41121061) supported by the Program for Innovative Research Group of Natural Science Foundation of China; Project(143GKDA007) supported by the Science and Technology Major Project of the Gansu Province; Project(SKLFSE-ZY-16) supported by the State Key Laboratory of Frozen Soil Engineering, China; Project supported by the West Light Foundation of CAS for G.Y. Li
Received date: 2015-03-25; Accepted date: 2015-11-09
Corresponding author: LI Guo-yu, Professor, PhD; Tel: +86-931-4967290; E-mail: guoyuli@lzb.ac.cn

