J. Cent. South Univ. Technol. (2007)02-0248-03

DOI: 10.1007/s11771-007-0049-5                                                                                             

Fitting methods for relaxation modulus of viscoelastic materials

DUAN Ji-an(段吉安), YANG Cheng-ling(杨成林), SHUAI Ci-jun(帅词俊)

(School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)          

Abstract: Based on viscoelastic theory, two new computational methods of solving linear equations and minimum value of the 1-norm were put forward for transforming Kohlrausch-William-Watts (KWW) function of viscoelastic materials to the generalized Maxwell model. The computational methods for the Maxwell model fitting were achieved in MATLAB software. It is found that fitting precision of the two methods is very high. The method of solving linear equations needs more fitting points and more numbers of Maxwell units. It makes the program of finite element analysis complex. While the method of solving minimum value of 1-norm can obtain very high precision only using less fitting points. These methods can fit not only experimental curve of KWW function, but also the experimental data directly.

Key words: viscoelastic material; relaxation modulus; Maxwell model; fitting                              

1 Introduction

With the application of new material and structure, the viscoelastic property that isn’t taken into account in the classic material mechanics and hydrodynamics has been highly regarded. Especially the high temperature creep has become the key question in the field of spaceflight, shipbuilding and so on. Meanwhile, visco- elastic theory and viscoelastic numerical analysis play a more and more important role in research of material science. Stress relaxation modulus expressed as generalized Maxwell model is required to analyze stress and strain with finite element method. While relaxation modulus data obtained from experiments or experiences are expressed as Kohlrausch-William-Watts (KWW) function, which is in an exponent-spread form. Before the engineering mechanics analysis and numerical calculation, it requires that KWW function fits generalized Maxwell model^[1-3]. The old method to confirm number of Maxwell model accords with the experimental curve. In this paper two methods of solving linear equation and minimum value of the 1-norm was put forward. The computational methods for the Maxwell model fitting were achieved in MATLAB software.

2 Generalized Maxwell model

The relaxation curve of viscoelastic material is an exponential damped function. Maxwell model can express the material relaxation rule. A simple Maxwell unit, which just has a relaxation time, cannot adequately describe relaxation modulus of a variety of material, while generalized Maxwell model can reflect the complex constitutive principle of stress relaxation of viscoelastic material. If applying a constant strain on the generalized Maxwell, its constitutive functions are^[4-5]

_{σ(t)=ε0G1(t)               (1)}

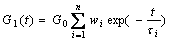         (2)

where  σ(t) is the Cauchy stress varied with time; G₁(t) is the stress relaxation function; G₀ is the initial shear modulus; n is the number of the Maxwell unit; τ_i= η_i/G_1, is the relaxation time of each Maxwell unit; and w_i is the relevant weight coefficient.

Material viscosity is relevant to its relaxation function, and can be described as

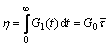          (3)

                   (4)

where  is the mean relaxation time.

It can be obtained from Eqns.(2) and (3) that

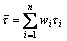                 (5)

Generalized Maxwell model provides the distinct interpretation of physical model. However, the number and parameters of Maxwell units cannot be directly determined by experiment data. Two or three Maxwell units can express explicitly the simple viscoelastic material, while the complex viscoelastic material requires more units. The number and parameters of Maxwell units are different in different materials. The same material also has different generalized Maxwell models because of equivalence principle of different parameters.

3 KWW Function

From the experimental data of different materials, it is found that most of material relaxation modulus could be described as empirical formula of Kohlrausch- William-Watts (KWW) function^[6-8]:

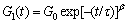              (6)

where  τ is the relaxation time, β(0≤β≤1) is the exponent-spread factor, and G₀ is the initial shear modulus.

KWW function can accurately express relaxation modulus of most materials. GEORGE pointed out that the value of exponent-spread factor β of most materials is between 0.4 and 0.8, β is a constant for a certain kind of material. It could be determined by experiments.

From Eqns.(6) and (3), we can obtain the relation between τ and:

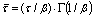            (7)

where  Γ is the gamma function.

KWW function, which is not a physical model of viscoelastic material, should be transformed into generalized Maxwell model in analyzing the rheological characteristics and carrying out numerical calculation.

4 Confirming parameters of Maxwell model

KWW function must fit generalized Maxwell model before numerical analysis. The question is turned into the equality of two matrixes, that is, Eqn.(2) must be turned into Eqn.(8):

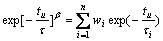     (u =1, 2, 3, … k)  (8)

where  k is the number of discrete time and n is the number of Maxwell unit. When u is from 1 to k, then k groups of equations are got. The matrix form is

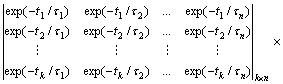
              (9)

noted as           [D][w]=[B]               (10)

The fitting aim is to determine Maxwell units n, relaxation time [τ] and relevant weighting coefficient [w].

To ensure the fitting precision of the two curves, the discrete time should be wide enough to cover the time spectrum. In this computing example, we take k=20. The values of two terminals should be set as follows:     

t₂₀/t₁=(0.2β)^1/β            (12)

The time spectrum t_k should take logarithmic distribution by using trial and error, that is,

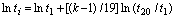       (13)

If t_k=τ_i, matrix D will be transmitted k dimension phalanx, which has one and only one solution ω.

As an example of fibreglass of 1 050 ℃(here β=0.5)^[5], the relaxation time and weight coefficient are solved. There are some small values in the solution of weight coefficient. They would be ignored if their values are less than 10^-4. The solution results are listed in Table 1 after adjusting.

It can be acquired from Eqn.(7) that:

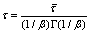              (14)

When the temperature is 1 050 ℃, the viscosity η is 10.25 Pa?s^[9-10], and the shear modulus is 31.4 GPa. Here the average relaxation time of fiberglass is 0.57 s. It can be acquired that τ=0.285 s. Substituting τ=0.285 s in Table 1, we can get the relaxation time τ_i and the relevant weight coefficient w_i of the optical fibreglass at this temperature.

Table 1 Relaxation time τ_i /τ and relevant weight coefficient w_i

Fig.1 shows that the method can get higher fitting precision. But the method of solving linear equations needs more fitting points and more numbers of Maxwell model. It will result in the program of finite element analysis complex, so the method of minimum value of the 1-norm is used to solve Eqn.(8).

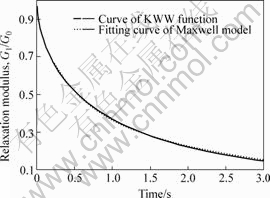
Fig.1 Fitting curve of relaxation time

5 Solving minimum value of 1-norm

If k is equal to n, the matrix D is the full rank matrix and the linear equations have a unique solution vector, thus

[w]=[D]^-1×[B]             (18)

If k＞n, the matrix D isn’t a full rank matrix and the linear equation doesn’t have a single solution vector, but we can solve the 1-norm of the equation group by pseudo inverse matrix:

[w]=Pinv([D])×[B]              (19)

where Pinv[D] is the pseudo inverse of matrix (general inverse matrix function). According to its property, the solution vector causes the error norm of the equation group to minimum. The definition is

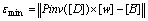             (20)

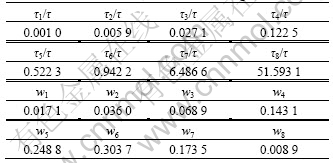
In this study, the simple method is used to optimize the minimum error norm ε_min, which could estimate the value of minimum error norm in different variants. When the root of the function is under the allowable error range, the program will stop searching and return to the result of searching vector and the function value. Fminsearch function in MATLAB software can realize the function to find minimum of 1-norm ε_min. By defining ε_min in Eqn.(20) as the searching function, discrete time vector as the searching vector, the initial time vector as [0.01 0 .05 0.5 1 10 50 200 400] and the function allowable error as 0.005, the relaxation time τ_i/τ and the relevant weight coefficient are solved while the number of Maxwell units is 8, which are listed in Table 2. The number of Maxwell units is less.

Table 2 Relaxation time τ_i/τ and relevant weigh coefficient w_i

6 Conclusions

1) Aimed at the question of KWW function transition to generalized Maxwell model, two new computational methods are brought forward by using MATLAB software. These methods can fit not only experimental curve of KWW function, but also the experimental data directly. This research provides foundation for engineering mechanics analysis and numerical calculation.

2) As an example of optical fiberglass, when the fusion temperature is 1 050℃ and the number of Maxwell unit is 12, the relaxation time is 0.000 4,  0.000 9, 0.002 6, 0.007 4, 0.020 6, 0.057 6, 0.161 0, 1.451 9, 1.265 3, 3.542 7, 9.919 2 and 27. 772 8; and the relevant weight coefficients are 0.006 1, 0.008 9, 0.014 9, 0.024 8, 0.041 5, 0.069 7, 0.113 4, 0.175 6, 0.239 3, 0.225 1, 0.077 2 and 0.001 0, respectively. When the number of Maxwell unit is 8, the relaxation time is  0.001 0, 0.005 9, 0.027 1, 0.122 5, 0.522 3, 0.942 2, 6.486 6 and 51.593 1; and the relevant weight coefficients are 0.017 1, 0.036 0, 0.068 9, 0.143 1,  0.248 8, 0.303 7, 0.173 5 and 0.008 9, respectively.

References

[1] THOMAS F S. Finite-element calculation of stresses in glass parts undergoing viscous relaxation[J]. J Am Ceram Soc, 1987, 70(2): 90-95.

[2] GEORGE W. Viscoelastic-elastic composites Ⅰ: General theory[J]. J Am Ceram Soc, 1982, 65(7): 352-360.

[3] SAKAGUCHI S. Viscosity of silica core optical fiber[J]. J Non-Crys Solids, 1999, 244(2): 232-237.

[4] HSUEH C H. Mathematical model of viscosity measurements for viscoelastic solids[J]. J Am Ceram Soc, 1986, 69(3): 48-49.

[5] ZARZYCKI J. Glasses and Amorphous Materials[M]. Beijing: China Science Press, 2002.(in Chinese)

[6] GEORGE W S. Volume relaxation far from equilibrium[J]. J Am Ceram Soc, 1986, 69(5): 374-381.

[7] HUANG Nan-nong. Creep deflection of viscoelastic laminated cylindrical panels with initial deflection under axial compression[J]. Composites: Part B, 1999, 30(5): 145-156.

[8] DOREMUS R H. Melt viscosities of silicate glasses[J]. J Am Ceram Soc, 2003, 82(3): 105-110.

[9] AGARWAL A, TOMOZAWA M. Surface and bulk structural relaxation kinetics of silica glass[J]. J Non-Cryst Solids, 1997, 209(3): 264-272.

[10] MICHAEL S, SIMON M S. Uniaxial, and biaxial stress relaxation functions[J]. J Am Ceram Soc, 1986, 69(9): 704-708.

Foundation item: Project (50605063) supported by the National Natural Science Foundation of China; Project(NCET-040753) supported by New Century Excellent Talents in University, China; Project (20050533037) supported by the Doctoral Program of Higher Education, China

Received date: 2006-06-14; Accepted date: 2006-07-23

Corresponding author: SHUAI Ci-jun, PhD; Tel: +86-731-8836858; E-mail:shuai@mail.csu.edu.cn

(Edited by YANG Bing)