Molecular dynamics simulation on plasticity deformation mechanism and

failure near void for magnesium alloy

ZENG Xiang-guo(曾祥国), XU Shu-sheng(许书生), CHEN Hua-yan(陈华燕), LI Ji-liang(李济良)

College of Architecture and Environment, Sichuan University, Chengdu 610065, China

Received 23 September 2009; accepted 30 January 2010

Abstract: The plastic deformation processes of magnesium alloys near a void at atomic scale level were examined through molecular dynamics (MD) simulation. The modified embedded atom method (MEAM) potentials were employed to characterize the interaction between atoms of the magnesium alloy specimen with only a void. The void growth and crystal failure processes for hexagonal close-packed (hcp) structure were observed. The calculating results reveal that the deformation mechanism near a void in magnesium alloy is a complex process. The passivation around the void, dislocation emission, and coalescence of the void and micro-cavities lead to rapid void growth.

Key words: magnesium alloy; void; molecular dynamics; plasticity deformation; failure

1 Introduction

Magnesium alloy which has a HCP crystal structure is widely used in aerospace industry, transportation, military industry, 3C fields and so on[1]. More and more experiments show that there are many micro-defects in the manufacturing process of magnesium alloys, including the voids, inclusions and micro-cracks, which will affect the mechanical properties of magnesium alloys significantly. Therefore, the deformation processes and failure mechanism around the micro-defects are the universal attention questions in engineering field and academy. But traditional finite element method (FEM) is not capable of describing this behaviour exactly. Thus, an effective computational method should be developed to characterize these crack propagation mechanisms. Molecular dynamics (MD) method can reproduce the macro-properties of a material, and store a great deal of valuable micro-information. Therefore, it was considered as an important tool to associate with the macro-scale and micro-scale[2]. Recently, as the continuous development of science and computer technology, the molecular dynamics method is widely applied to analyze crack propagation mechanisms. It seems that molecular dynamics can be a powerful tool for investigating atomic scale mechanical behaviours at a micro-defect front. In recent years, there are many publications in this field[3-11], which deal with either body-centred cubic (BCC) or face-centred cubic (FCC) crystal structure materials. KOTRECHKO et al[12] and HUANG et al[13] investigated the fracture process of nano-crystal materials under axial tension and illuminated the tensile mechanical properties of nano-materials, respectively. KITAMURA et al[14] and IKEDA et al[15] investigated the fracture behaviour of different materials and proposed the fracture criterion, which can be used to estimate the critical conditions of crack propagation. They obtained the growth mechanism on the front of a micro-defect and the fracture procedure in both BCC and FCC materials. Yet, relatively less work has been carried out on the hexagonal close-packed (HCP) materials because of the complexity of HCP crystal structure.

In this work, the propagation process near a void on magnesium alloy at an atomic level under external load is examined using a molecular dynamics simulation. The modified embedded atom method (MEAM) potentials are employed in the simulation to characterize the inter-atomic interactions. The whole calculation is performed by large-scale atomic/molecular massively parallel simulator (LAMMPS)[16]. 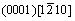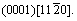Micro-vacancies are observed during the simulation, as well as dislocation emission around the void along the slip systems of HCP crystal structure, andThe calculating results reveal that the passivation around the void, dislocation emission, and coalescence of the voidand micro-cavities will induce the void growth.

2 Modified embedded atom method

It is known that choosing potential functions is essential in a molecular dynamics simulation. Lots of many-body potentials have been developed to approximate the interactions of atoms, such as Tersoff, embedded atom method (EAM), and modified EAM. In this study, the modified embedded atom method (MEAM) potential was used to characterize the interactions of atoms. Conceptually, it is an extension to the original EAM potentials which adds angular forces. Thus, it is suitable for modeling metals and alloys with FCC, BCC and HCP structures, as well as covalently bonded materials like silicon and carbon. The total energy E of a system in the embedding atom method is given by an approximation form[17]:

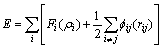                   (1)

where F_i is energy to embed an atom of type i into the background electron density at site i, ρ_i is the electron density, and  is a pair potential interaction between atoms i and j whose separation is given by r_ij.

For a HCP structure with ideal c/a ratio, the equilibrium electron density ρ_e can be expressed as[18]

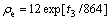                           (2)

where t₃ reflects the deficiency of inversion symmetry in HCP crystal structure, and the embed function F is given by the form:

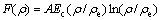                   (3)

where A, E_c are the BCC-HCP energy difference and cohesive energy, respectively, and the electron density ρ is

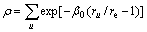                     (4)

where the superscripts u refers to neighboring atoms to the site in question.

The pair potential interaction 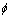 is given:

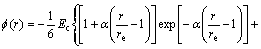
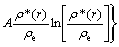                   (5)

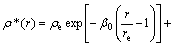
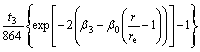       (6)

where α, β are the adjustable potential parameters.

The parameters in the MEAM model are determined by the elastic constant of materials, cohesive energy, and bulk modulus[18]. The input parameters of magnesium are given in Table 1.

Table 1 MEAM input parameters of magnesium alloy

3 Molecular dynamics (MD) simulation

3.1 MD model

The crystal style of magnesium is hexagonal close-packed (HCP), with lattice constant a=b=0.302 94 nm, c=0.521 05 nm, α=β=90?, γ=120?. The three slip systems of magnesium are 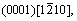 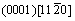and 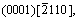 as shown in Fig.1. Experiments show that there are many voids in the manufacturing process of magnesium alloys which affect the mechanical properties of magnesium alloys significantly, as shown in Fig.2. Therefore, this work focus on the plastic deformation and failure mechanism of magnesium specimen with a void in the center under external loading.

The MD model consists of 18 042 atoms with size of 11.55 nm×16.05 nm×1.56 nm. The whole simulation area is divided into three parts, which are the upper and lower boundary region with three atom layers respectively, and the molecular dynamics relaxation region with a void of 1.93 nm in size at the centreline along x axis. In LAMMPS, one can effectively create a void in a simulation by deleting the atoms at specified region using the “delete atom” command. The molecular dynamics model adopted is shown in Fig.3.

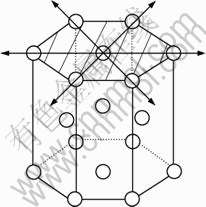
Fig.1 Crystal structure of magnesium and its slip systems

3.2 Solving process

The boundary condition of the model along y and z axis is free-surface, and x orientation is periodic. The

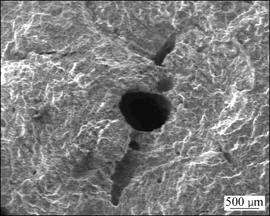
Fig.2 Voids in magnesium alloys

Fig.3 Molecular dynamics (MD) model

initial temperature of the system is 0 K. The loading process is divided into two steps: in the first loading step, the system is relaxed with 2 000 time steps to perform an energy minimization of the system, and in the second loading step, a velocity is imposed along y axis at 0.04 μm/ps, and the total step is 8 000 with a time step at 2.045 fs. Utilize the velocity-verlet algorithm to solve the Newton’s motion equations and keep a record of the atomic configuration every 300 time steps during the simulation.

The velocity-verlet algorithm is given by[20]

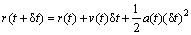               (7)

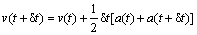              (8)

The solving process of this algorithm accord to the following procedures:

Step 1: Give the initial spatial positions of all the atoms.

Step 2: Give the initial velocity.

Step 3: Give a very small time increment δt, and calculate the atom positions at time t+δt by Eq.(7), as well as the velocity.

Step 4: Return to Step 2 and start to solve the position at the next time.

4 Simulation results

From the simulation procedure, it can be seen that the atoms near the void are disordered after the external loading applied. At the initial time step, the void does not grow because of the relatively low load. With the increase of loading, the disordered area extends to the internal of crystal structure, vacancies and micro-cavities form and the void grows along horizontal orientation. It can be also observed that the dislocation forms and emits around the void along the slip systems of HCP structure 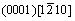and 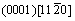. The coalescence of the void and micro-cavities leads to void growth rapidly.

Fig.4 illustrates the geometry of the system at different time steps during the MD simulation. It can be seen that at the initial time step, all the atoms arrange regularly according to the ideal lattice. The atomic arrangement becomes disordered after the external load is applied, and the disordered areas expand constantly with the increase of load. At a low stress level of time step 1 500, the void starts to blunt and the top and bottom void surface bend. Then, the disordered areas continue to expand to the internal of crystal, and the blunting phenomenon is more obvious at the time step 4 500. At time step 5 700, the vacancies form with further increasing of external load. The void becomes unstable and starts to grow, meanwhile dislocation forms and emits along the slip systems. This can be explained from atomic viewpoint. While the local stress exceeds the critical value of unstable propagation, the chemical bonds with weaker cohesive force break, thus, the void grows. At time step 7 200, micro-cavities initiate and grow gradually with further increasing of external load. The coalescence between the micro cavities at the front of void induces the void growth rapidly. The void keeps on propagating with the increasing of load, and at last, the crystal structure failures, as shown in Fig.4(e).

5 Conclusions

1) One can establish an effective micro-model to carry out a molecular dynamics simulation to analyze the fracture behaviour and failure mechanism of magnesium based on the appropriate potentials.

2) The void gets blunt at first, then vacancies form and the void starts to grow with increasing of external load, together with the dislocation emissions along slip systems, at last, coalescence of the void and micro cavities induce the void growth rapidly and failure occurs.

Fig.4 Geometry of system at different load steps: (a) 1 500; (b) 4 500; (c) 5 700; (d) 7 200; (e) 8 000

3) The results and analysis method provide a new approach to explain the material destruction in practical engineering, which can take on an important reference for the researchers in this filed.

References

[1] SHI Chang-xu, LI Heng-de, WANG Dian-zuo, LI Yi-yi, ZUO Tie-yong. A proposal on accelerating development of metallic magnesium industry in China [J]. Materials Review, 2001,15(4): 5-6. (in Chinese)

[2] YU Tao, XIE Hong-xian, DU Jun-ping, CAO Li-xia, WANG Chong-yu. Progress of investigation on crack dynamics [J]. Metallic Functional Materials, 2008, 15(3): 39-42. (in Chinese)

[3] RAFII-TABARA H, SHODJA H M, DARABI M, DAHI A. Molecular dynamics simulation of crack propagation in fcc materials containing clusters of impurities [J]. Mechanics of Materials, 2006, 38: 243-252.

[4] GUO Ya-fang, WANG Yue-sheng, ZHAO Dong-liang. Atomistic simulation of stress-induced phase transformation and recrystallization at the crack tip in bcc iron [J]. Acta Materialia, 2007, 55: 401-407.

[5] LUO Jin, ZHU Wen-jun, LIN Li-bin, HE Hong-liang, JING Fu-qian. Molecular dynamics simulation of void growth in single crystal copper under uniaxial impacting [J]. Acta Physica Sinica, 2005, 54(6): 2791-2798. (in Chinese)

[6] CHEN Jun, XU Yun, CHEN Dong-quan, SUN Jin-shan. Multi-scale simulation of the dynamic behaviors of nano-void in shocked material [J]. Acta Physica Sinica, 2008, 57(10): 6437-6443. (in Chinese)

[7] NISHIMURA K, MIYAZAKI N. Molecular dynamics simulation of crack growth under cyclic loading [J]. Computational Materials Science, 2004, 31: 269-278.

[8] INAMURA T, TAKEZAWA N, SHIBUYA K, YAMADA K. Dynamic phenomena at mode-I crack front in silicon simulated by extended molecular dynamics [J]. Annals of the CIRP, 2007, 56: 561-564.

[9] DECELIS B, ARGON A S, YIP S. Molecular dynamics simulation of crack tip processes in alpha-iron and copper [J]. J Appl Phys, 1983, 54: 4864-4878.

[10] GUO Ya-fang, GAO Suo-wen. Atomistic simulation of crack propagation and its size-dependent behavior [J]. Journal of Beijing Jiaotong University, 2005, 29(4): 5-9. (in Chinese)

[11] SWADENER J G, BASKES M I, NASTASI M. Molecular dynamics simulation of brittle fracture in silicon [J]. Phys Rev Lett, 2002, 89(8): 1-4.

[12] KOTRECHKO S A, FILATOV A V, OVSJANNIKOV A V. Molecular dynamics simulation of deformation and failure of nanocrystals of bcc metals [J]. Theoretical and Applied Fracture Mechanics, 2006, 45: 92-99.

[13] HUANG Dan, TAO Wei-ming, GUO Yi-mu. Molecular dynamics simulation of failure process of nano aluminum wire under axial tension [J]. Ordnance Material Science and Engineering, 2005, 28(3): 1-4. (in Chinese)

[14] KITAMURA T, HIRAKATE H, SATAKE Y. Applicability of fracture mechanics on brittle delamination of nanoscale film edge [J]. JSME International Journal (Series A), 2004, 47(2): 106-112.

[15] IKEDA T, MIYAZAKI N. Mixed mode fracture criterion of interface crack between dissimilar material [J]. Engineering Fracture Mechanics, 1998, 59(6): 725-735.

[16] PLIMPTON S J. Fast parallel algorithms for short-range molecular dynamics [J]. J Comp Phys, 1995, 117: 1-19.

[17] Information on http://lammps.sandia.gov.

[18] BASKES M I. Modified embedded-atom potentials for cubic materials and impurities [J]. Physical Review B, 1992, 46(5): 2727-2742.

[19] BASKES M I, JOHNSON R A. Modified embedded atom potentials for HCP metals [J]. Modeling Simul Mater Sci Eng, 1994, 2: 147-163.

[20] SWOPE W C, ANDERSEN H C, BERENS P H, WILSON K R. A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: Application to small water clusters [J]. J Chem Phys, 1982, 76(1): 637-649.

(Edited by CHEN Ai-hua)

Foundation item: Project(10776023) supported by the National Natural Science Foundation of China

Corresponding author: XU Shu-sheng; Tell: +86-13540837519; E-mail: xuss515361@163.com