J. Cent. South Univ. (2021) 28: 954-967

DOI: https://doi.org/10.1007/s11771-021-4656-3

Non-linear creep damage model of sandstone under freeze-thaw cycle

LI Jie-lin(Àî½ÜÁÖ)^{1, 2, 3}, ZHU Long-yin(ÖìÁúØ·)^{1, 2, 3, 4}, ZHOU Ke-ping(ÖÜ¿Æƽ)^{1, 2},

CHEN Hui(³Â»Ô)^{1, 5}, GAO Le(¸ßÀÖ)^{1, 2}, LIN Yun(ÁÖÔÊ)^{1, 2}, SHEN Yan-jun(ÉêÑÞ¾ü)⁶

1. School of Resource and Safety Engineering, Central South University, Changsha 410083, China;

2. Research Center for Mining Engineering and Technology in Cold Regions,Central South University, China;

3. Key Laboratory of Rock Mechanics and Geohazards of Zhejiang Province, Shaoxing 312000, China;

4. Northern Engineering & Technology Corporation, China Metallurgical Group Corporation,Dalian 116000, China;

5. School of Geology and Mining Engineering, Xinjiang University, Wulumuqi 830046, China;

6. College of Architecture and Civil Engineering, Xi¡¯an University of Science and Technology,Xi¡¯an 710054, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021

Abstract: To study rock damage characteristics under long-term freeze-thaw cycles and loads, rock freeze-thaw and creep damage factors were defined based on nuclear magnetic resonance porosity and volume strain, respectively. The damage factor is introduced into the basic rheological element, and the non-linear creep damage constitutive model and freeze-thaw rock equation are established to describe non-linear creep characteristics under a constant load. Simultaneously, the creep test of freeze-thaw rock under step loading is performed. Based on the test data, the applicability and accuracy of the creep damage freeze-thaw rock model are analyzed and verified. The results show that freeze-thaw cycles result in continuous rock pore structure damage and deterioration, and nuclear magnetic resonance porosity enhancement. The constant load induces increasing rock plastic deformation, volume, and creep aging damage. As the loading stress increases, the instantaneous rock elastic parameters increase, and the rheological elastic and viscosity parameters decrease. Furthermore, the damage degradation of freeze-thaw cycles weakens the rock viscoplasticity, resulting in a rapid decrease in the viscosity parameter with an increase in freeze-thaw cycles. Generally, the continuous damage of the rock is degraded, and the long-term strength decreases continuously.

Key words: aging damage; creep damage model; damage factor; stable creep

Cite this article as: LI Jie-lin, ZHU Long-yin, ZHOU Ke-ping, CHEN Hui, GAO Le, LIN Yun, SHEN Yan-jun. Non-linear creep damage model of sandstone under freeze¨Cthaw cycle [J]. Journal of Central South University, 2021, 28(3): 954-967. DOI: https://doi.org/10.1007/s11771-021-4656-3.

1 Introduction

With the development of the social economy, cold areas will witness a large number of open-pit mines, railways, highways, tunnels, and other geotechnical projects [1]. During the construction of engineering projects in cold regions, the ground will inevitably undergo freezing and thawing disasters, such as frozen soil layer, frozen rock layer, freezing expansion, and thawing settlement caused by heat and cold exchange [2, 3]. Under the action of freeze-thaw cycles, rock mass will undergo damage and deterioration, causing rock mass freeze-thaw denudation, slide, and even slope landslide, seriously affecting stability [4]. Geotechnical engineering in cold regions also subjects the rock mass to the long-term effects of self-weight stress, original rock stress, and external load, causing its deformation characteristics to change slowly over time. The aging characteristics of rock have a great influence on the long-term stability of the project [5, 6]. In the mining process of open-pit mine in cold area, the rock slope is exposed in the external environment for a long time, which is easy to be eroded by freeze-thaw cycle, resulting in rock fall, flying rock and even collapse, which seriously affects the operation safety of the lower part of the stope. In view of the stability of mine slope in cold region, the long-term effect of freeze-thaw cycle and self weight stress should be fully considered. Therefore, the study of rock long-term strength characteristics under freeze-thaw and long-term load helps to reveal the deformation and instability mechanism and reduce the freeze-thaw disaster experienced during mine slope engineering in cold regions.

The rheological properties of rocks refer to the aging deformation characteristics of rock under conditions of force, temperature, and radiation [7]. Presently, researches on rock creep damage characteristics mainly focused on rock creep testing and creep modelling. DAVID [8] first carried out creep testing of limestone, shale, and siltstone. FU [9] theoretically explained the rheological, relaxation, and dilatancy characteristics of rocks. TOSHIHISA et al [10] conducted a saturated water creep test using sedimentary soft rock and proposed a method for predicting the long-term strength of soft rock based on the creep test. ZHAO et al [11] conducted a uniaxial compression and grading loading creep test of red sandstone and summarized the creep deformation characteristics of rock. ZHAO et al [12] conducted a triaxial creep test on the multi-stage loading and unloading cycle of marble, pointing out that closed stress and creep expansion are the two basic factors.

A series of rock creep studies show that the basic creep components can be used to form a corresponding creep model, which can reasonably and effectively describe many rock creep laws [13]. Component combination models can be classified into four types: cohesive, viscoelastic, viscous, and viscoplastic models [14]. The mechanical parameters (such as elastic modulus, viscous coefficient, yield strength, etc.) in these constitutive models, which are linear constitutive models, are generally assumed to be constant [15]. However, due to the heterogeneity of rock materials, the mechanical parameters tend to exhibit non-linear characteristics with time [16]. Therefore, many rock nonlinear rheological models using new non-linear rheological components or introducing internal time theory and damage theory have been established [17, 18], such as the modified Kelvin model based on non-Newtonian fluid [19], classical combined model considering aging damage [20], non-linear rheological model with damage factor introduced [21], and internal rheological equation of soft rock based on internal time theory [22].

Related studies have shown that the freeze-thaw cycle has an important effect on the weakening of the long-term rock strength, which is related to rock properties, pore structure, initial damage, and other factors [23]. Under the action of freezing and thawing, the internal structure of rock undergoes continuous damage and deterioration. When the damage effect accumulates beyond a certain extent, it will affect the macroscopic mechanical properties of the rock and reduce its strength [24]. Therefore, mesoscopic parameters are used as the freeze-thaw damage factor, and the non-linear creep damage model is established in the creep model of freeze-thaw rock, which can describe the non-linear variation of freeze-thaw rock under constant load. They can accurately reflect the macroscopic damage characteristics of rock [25]. When the basic creep model introduces the damage factor to express the non-linear characteristics of the parameters, the constitutive relation of the linear element is simultaneously transformed into non-linear, and the creep equation becomes a non-linear equation [26]. In the direction of the research, XU [27] found the time-dependent relationship between rock creep and elastic model, and proposed the corresponding mathematical relationship. XU et al [28] proposed a rock brittle creep model based on aging damage, and revealed the law of microscopic crack propagation damage by numerical calculation. YANG et al [29] established an elastic and viscous element based on aging damage, and introduced the damage element into the Nishihara model, so the model can accurately describe the damage characteristics of the whole process of rock creep. The main application of these non-linear equations is rock creep under normal conditions. The creep properties of rocks under freeze-thaw cycles still need to be further studied.

Therefore, based on the research of creep damage model, a non-linear creep damage model is established, which can well describe the non-linear variation law of freeze-thaw rock under constant load. Therefore, a creep model based on the meso-damage factor is established. The damage factors of freeze-thaw and creep are defined by the rock meso-damage characteristics, and the non-linear creep constitutive equation of freeze-thaw rocks is derived. Simultaneously, combined with the creep test results of freeze-thaw rock under step loading, the variation characteristics of various parameters of the creep model are analyzed to reveal the damage degradation law of the long-term strength of rock under freeze-thaw conditions and long-term loading.

2 Determination of creep damage variable of freeze-thaw rock

2.1 Damage characteristics of meso-structure under freeze-thaw action

Under the action of freezing and thawing, pore water in rock undergoes the process of freezing expansion and melting shrinkage, which causes damage to the rock¡¯s pore structure, thus affecting the overall strength characteristics [30]. As the number of freeze-thaw cycles increases, the damage to the internal structure of the rock increases, and the long-term strength of the rock decreases. It is assumed that the original pore volume in the sandstone rock sample is V_i⁰; and the pore volume after the n times freeze-thaw cycle is V_iⁿ; the amount of change in the pore volume of the rock sample caused by freeze-thaw action is ¡÷V_i:

                            (1)

It is assumed that the original volume of the sandstone rock sample is V⁰, which is composed of the internal pores of the rock and the rock skeleton. Ignoring the change of the rock skeleton volume caused by the freeze-thaw cycle, the rock volume V ⁿ after the freeze-thaw cycle is:

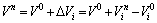                  (2)

According to the definition of porosity, the porosities f₀ and f_n of the rock sample undergoing each undergoing 0 and n times of freezing and thawing cycles is:

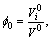
               (3)

It can be known from Eq. (3) that there is a significant correlation between the degree of freeze-thaw damage and porosity of rocks.

According to the classical damage theory of rocks, the freeze-thaw damage variable can be defined as the ratio of the defect area to the total area of the section perpendicular to the direction of force:

                                 (4)

where D is the damage variable; A is the cross- sectional defect area; and A₀ is the cross-sectional area.

Because of the sandstone, as a porous medium material, the pores in certain section can be regarded as defects. Therefore, A/A₀ is the surface porosity of the section, which is the rock freeze-thaw damage variable.

The pore structure of sandstone is very complex, and it is difficult to accurately describe the geometric characteristics of the pore structure inside the rock. Therefore, in order to accurately describe the pore distribution of sandstone, the porosity is defined as a continuous function. Taking a series of volume micro-elements V_c^s (s=1, 2, 3, ¡­) around any point P inside the rock, the volume of these volume micro-element gradually decreases, i.e., V_c¹>V_c²>V_c³>V_c⁴>¡­. The porosity of these volume micro-elements f_i (i=1, 2, 3, ¡­) constitutes the V_c- f_i coordinate system, and the corresponding curves are obtained as shown in Figure 1 [31, 32].

As the volume micro-element increases, the fluctuation of porosity decreases. When the characteristic micro-element reaches V_c, the porosity is a horizontal straight line. At this time, the porosity of the characteristic micro-elements is the rock porosity. The characteristic micro-element V_c needs to meet two conditions, namely much larger than a single pore volume and much smaller than the size of the rock.

Figure 1 Relationship between porosity and characteristic volume micro-element

There is a certain relationship between the surface porosity and the volume porosity. For a volume microelement of a cylinder, the pore area of its cross section is A_n and the phase length of the voxel section method is l:

 (5)

whereis the average value along the axis of the cylinder.

If the characteristic element V_c is not a cylinder, but an arbitrary shape, then Eq. (5) can be transformed into:

      (6)

It shows that the volume porosity of any volume micro-element in the porous medium is equal to the average value of the surface porosity in this direction, and the porosity is a scalar quantity, which can be simplified as:

                                  (7)

Combining Eq. (4) and (7), freeze-thaw damage can be expressed as:

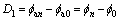                       (8)

where f_a0 is the rock undergoing 0 freeze- thaw cycles; f_an is the rock undergoing n freeze-thaw cycles.

2.2 Evolution equation of creep aging damage of frozen-thawed rock

There are various microscopic defects such as pores, microcracks, and voids inside sandstone. Under the action of the load, these mesoscopic defects undergo an irreversible degradation process, which will cause rock deformation and damage [33]. During the creep loading process, the transverse and longitudinal strains are constantly changing, resulting in a continuous increase in the volumetric strain of the rock. Assuming that the rock skeleton volume does not change with stress, the rock volume change before and after constant loading is:

                              (9)

where V is the rock total volume before constant loading; and V' is the rock volume after constant loading; ¡÷V is the volume change in the rock.

The porosity changes before and after constant loading are:

                     (10)

where V_m is the volume of rock pore before constant loading.

The strain of rock mass under loading is:

                               (11)

where ¦Å_v is the rock strain.

According to recent research results, during the creep loading process, the rock volume change is much smaller than the rock volume. Hence, the total rock volume is unchanged [34].

                 (12)

According to Eqs. (4), (6) and (7), the creep damage variable of rock is:

                          (13)

Figure 2 shows the volume strain curve of sandstone at different loading time. The volume strain of rock varies non-linearly with time in the process of constant load loading.

The exponential function can be used for fitting analysis. Meanwhile, the damage evolution equation is obtained as follows:

                       (14)

Figure 2 Curve of volume strain of sandstone at different loading time

where D₂ is the creep aging damage of rock; and a₀, b, and ¦Á are the coefficients related to the degree of damage. Using the above damage evolution equation, the fitting curve of the experimental values can be obtained, with a fitting correlation coefficient of 0.96, which indicates that the damage evolution equation can well describe the variation law of rock volume strain during creep loading.

Assuming that the material undergoes homosexual damage and the damage law of each parameter is the same, the change in any creep parameter A(t) over time can be expressed as:

          (15)

where A₀ is the initial value of the parameter.

In the basic creep model element, the parameters of the elastic element and viscous element have characteristics that are clearly non-linear. According to Eq. (14), the corresponding non-linear expressions of creep parameters of damaged element can be obtained as follows:

            (16)

            (17)

where E is the modulus of elasticity; and ¦Ç is the viscosity coefficient.

2.3 Creep damage evolution equation of freeze- thaw rock

According to the Lemaitre strain equivalence principle and the concept of effective stress, the constitutive relation of the material in any damage state is the same [35]. The initial damage state of rock is regarded as the benchmark damage state, and the generalized strain equivalence principle is proposed [36]. In this paper, the damage state of rock after freeze-thaw is regarded as the first damage state, and the damage caused by freeze-thaw loading is regarded as the second damage state [37]. Therefore, the constitutive relationship of rock under freeze-thaw conditions and the loading state can be obtained as follows:

                          (18)

                           (19)

By substituting Eqs. (8) and (14) into Eqs. (18) and (19), the stress-strain relationship of frozen- thawed loaded rocks can be obtained as follows [38]:

          (20)

                       (21)

where E₀ and E are the elastic moduli; ¦Ò is the stress component; ¦Å is the strain component; D₀ is the total damage of the rock freeze-thaw load.

3 Constitutive model of rock creep damage considering freeze-thaw cycles

3.1 Common damage model

At present, commonly used damage models include Maxwell model, Kelvin model, Bingham model, village mountain model, nishihara model, etc [39]. These damage models are composed of several elastic elements and viscous elements in series and parallel, so Kelvin model and Maxwell model are selected to analyze.

The classical Kelvin model is composed of elastic elements and viscous elements in parallel, and the damage equations are:

                 (22)

                       (23)

In the rock creep model established by the classical Kelvin model, the elastic parameter is a linear element, and the viscosity parameter is the derivative of time, which cannot well represent the non-linear characteristics of creep, so it is necessary to introduce the damage factor to describe the non-linear characteristics of the model [40]. Combining Eqs. (20) and (23), a non-linear Kelvin model considering the effects of freeze-thaw and aging damage can be obtained. The specific damage equation is as follows:

                 (24)

Figure 3 shows the main features and excellence of the non-linear Kelvin model. In the initial stage of creep, the creep variables of the two models are not much different, but as the creep time increases, the aging damage of the non-linear Kelvin model is intensified, and the damage is constant at infinity, and the asymptote of the damage is a curve. The creep asymptote of the classic Kelvin model is a straight line. In the nonlinear Kelvin model, the rheological parameters E and ¦Ç of elastic and viscous components are all functions including aging damage factors, and the parameters E and ¦Ç in the aging damage function are constant. The nonlinear characteristics of creep parameters can be characterized by aging damage function, which can simplify the relationship between model parameters and obtain a more accurate and real creep model.

Figure 3 Creep curves of different Kelvin models

The Maxwell model is composed of elastic elements and plastic elements in series, and the creep damage equations are:

                              (25)

                            (26)

In the classical Maxwell model, there is an instantaneous elastic strain in the model, and the viscous strain increases uniformly with time. Under the action of constant stress, the stress-strain change of rock is non-linear, and the strain tends to be constant after a certain time. The classical Maxwell model cannot accurately describe the creep strain change of rock. Combining Eqs. (20) and (23), a non-linear Maxwell model considering the effects of freeze-thaw and aging damage can be obtained. The specific damage equation is as follows:

                    (27)

As shown in Figure 4, the creep curves of different Maxwell models are quite different. The classical Maxwell model is a straight line, and the non-linear Maxwell model is a curve with increasing slope. It can be seen that as the creep time increases, the non-linear equation has a faster and larger deformation, which is an accelerated creep curve, which can be used as the constitutive equation to describe the accelerated creep. However, due to the extreme value of rock damage, this model is not very accurate in describing the failure state inthisexperience.

Figure 4 Creep curves of different Maxwell models

3.2 Creep model of freeze-thaw rock based on damage variable

Based on the test data, the sandstone is brittle rock, and its stress-strain curve can be divided into elastic deformation section and elastic-plastic deformation section. So, this paper uses the instantaneous elastic body to represent the elastic deformation, introduces the non-linear Kelvin damage model to describe the elastoplastic deformation, and introduces non-linear rheological elements to describe the rock accelerated creep. A five-element non-linear damage model with variable parameters is established to describe the creep characteristics of freeze-thaw rock. The physical meaning of each component of the model is clear, and can be used to analyze the variation law of rock physical and mechanical parameters during the creep process [41, 42]. The model is shown in Figure 5.

Figure 5 Five-element creep damage model of freeze-thaw rock

According to the constitutive model shown in Figure 5, the corresponding equation of state is:

                    (28)

where ¦Å is the total creep strain; E₁ and E₂ are the elastic parameters; ¦Ç₁ and ¦Ç₂ are the viscous coefficients; and n is the HVPB component parameter.

1) According to the constitutive equation of the creep model of freeze-thaw rock, only the transient elastic element acts in the model during rock loading. Because elastic strain can occur in a short time, and the viscous deformation is related to the loading time, there is no need to consider the rock damage caused by the time effect. Therefore, the corresponding constitutive equation is:

               (29)

2) When the frozen-thawed rock is loaded to a constant load and its strength is less than its long-term strength (¦Ò₀¡Ü¦Ò_s, ¦Ò_s is the long-term strength of the rock), the rock finally resides in a stable creep phase. The first and second parts of the model are used to characterize the rock creep deformation characteristics, wherein the instantaneous elastic element is not affected by the aging damage. At this time, the damage factors of the rock include freeze-thaw damage and aging damage. The damage equation is:

          (30)

3) When the frozen-thawed rock is loaded to a constant load and is greater than its long-term strength (¦Ò₀>¦Ò_s), the rock is in the accelerated creep stage. As time goes on, the macroscopic damage is finally caused. The creep constitutive equation is:

 (31)

The above is the constitutive equation of the nonlinear creep model of the frozen-thawed rock based on the damage variable. This model can describe the deformation characteristics of freeze-thaw rock during creep loading under different stress conditions, and at different time, and has wide applicabilities.

4 Verification and analysis of creep model of freeze-thaw rock

4.1 Uniaxial compression creep test of freeze- thawed rock

To verify the accuracy of the above-mentioned non-linear creep model of freeze-thaw rock, the quartz sandstone from Gansu province, China, was selected for freeze-thaw cycle and creep test. The physical and mechanical parameters of sandstones are shown in Table 1.

Table 1 Basic physical and mechanical parameters of sandstone samples

The specific test processes are:

1) The rock samples were immersed in distilled water, and the freeze-thaw cycle experiment was then completed with a TDS-300 freeze-thaw cycle machine. The annual average daily maximum temperature was 16 ¡ãC and the minimum temperature was -8 ¡ãC in Gannan area, China. So the freezing temperature was -10 ¡ãC, the thawing temperature was 20 ¡ãC, and the freezing and thawing periods were each 4 h; that is, each freeze-thaw cycle was 8 h. A testing cycle included 0, 5, 10 freeze-thaw cycles.

2) After each testing cycle, nuclear magnetic resonance (NMR) testing was conducted to determine the changes in porosity before and after each rock freeze-thaw cycle.

3) The step loading test used a rock shear rheometer (RYL-600). The creep loading method adopted the ¡°Chen¡¯s loading method¡±, and the total load was predicted according to the uniaxial compressive strength of the rock specimens. The results of uniaxial compression test of rock are shown in Table 2.

Table 2 Uniaxial compressive strength of sandstone samples

The uniaxial compressive strength of rock has large dispersion, and the minimum value is 27.58 MPa. So the creep test load was 30%, 40%, 50%, 60%, respectively of the average value of the rock. The grading loading stress is 13.18, 17.57, 21.97 and 26.36 MPa, respectively, and the rock transverse and longitudinal strains are recorded using a strain gauge during the loading process. The loading rate per stage is 100 N/s. Test flow chart is shown in Figure 6. The grading loading creep test curve of freeze-thawed rock is shown in Figure 7. The rock strain change during loading is shown in Figure 8.

According to the NMR test results of freeze-thawed rock, the porosity of the rock subjected to 0 freeze-thaw cycles is 11.0%, the porosity of the rock before and after 5 freeze-thaw cycles is 12.7% and 13.5%, respectively, and the porosity of rocks before and after 10 freeze-thaw cycles is 11.0% and 14.3%, respectively. This shows that as the number of freeze-thaw cycles increases, the pore structure inside the rock is continuously destroyed, and the porosity becomes larger, resulting in an increase in the initial damage D1.

Figure 8 shows that under constant load loading, the transverse strain of the freeze-thaw rock increases continuously, the longitudinal strain continues to decrease, and the volume strain of the rock decreases first and then increases. In the freeze-thaw rock loading section, the rock is compressed to produce elastic deformation, and the volume is reduced. When loaded into the creep section, the rock undergoes plastic deformation and expands, resulting in an increase in volume. In addition, the rock plastic deformation is unrecoverable, which results in the damage to and destruction of the internal structure of rock. Therefore, in the creep section of freeze-thaw rock, the rock volume strain is used as the creep damage variable, which can better describe the creep damage evolution characteristics.

Figure 6 Flow chart of freeze-thaw rock creep test

Figure 7 Rock uniaxial compression grading loading creep curve

Figure 8 Changes of transverse, longitudinal and volumetric strains of rocks during loading

4.2 Determination of damage variables

According to the strain data of the creep loading test of freeze-thawed rock, the fitting analysis was carried out by Eq. (6), and the damage variables under different freezing and thawing cycles, and different loading stresses were obtained, as shown in Table 3.

Table 3 demonstrates that as the number of freeze-thaw cycles increases, the freeze-thaw damage of the rock increases rapidly, with 5 cycles yielding a freeze-thaw damage of 0.8% and 10 cycles giving a freeze-thaw damage of 3.3%.

Table 3 Damage variable parameters of freeze-thaw rock

Simultaneously, during the creep loading process, the aging damage variable a₀ also grows rapidly, with 0 freeze-thaw cycle below 0.1%, 5 freeze-thaw cycles between 0.1% and 0.2%, and 10 freeze-thaw cycles between 0.4% and 0.6%. This shows that under the action of freezing and thawing, rock plasticity is continuously enhanced, resulting in a continuous increase in the rock volume under constant load, continuous damage of the pore structure inside the rock, and an increase in the damage variable.

4.3 Parameter identification and analysis of rock creep model

According to the creep test curve shown in Figure 7, combined with the relationship of the damage variables in Table 3, the fitting validation curves are obtained after processing the experimental data by using Eqs. (25) and (26). The parameters of the creep model of freeze-thaw rock are shown in Figure 9 and Table 4.

The fitting results in Figure 9 show that the creep model determined by the porosity-based freeze-thaw rock damage variable can reflect the non-linear characteristics of creep deformation of freeze-thaw rock during loading. The damage factor is introduced into the non-linear creep model to consider the aging damage degradation effect, and the different factors of creep damage are fully considered. This has the advantages of a simple model and clear physical meaning of parameters.

The variation of different freeze-thaw cycles and loading stress model parameters are shown in Figure 10. The instantaneous elastic parameters of rock are basically unchanged with the increase of freeze-thaw cycles. The instantaneous elastic parameter E₁ increases exponentially with the increase in constant load. Under low stress conditions, the elastic parameters under loading are controlled by the initial modulus of rock. With the increase in the stress level, the elastic parameters tend to tangent modulus gradually, such that no drastic changes occur. With the increase of freeze-thaw cycles, the elastic parameter E₂ of rock decreases continuously. The distribution of viscosity parameter ¦Ç₂ is not regular, but it shows a decreasing trend. It can be explained that when the loading enters the elastic-plastic stage, the instantaneous elastic deformation of the rock will not occur, but the viscoplastic deformation will be caused by the relative movement between the particles in the rock, which is determined by the microscopic characteristics of the rock particles. Under the action of freezing and thawing, the pore water in the rock expands and melts, resulting in the relative movement of rock particles around the pores, which changes the meso distribution characteristics of rock particles and causes the damage and deterioration of the whole rock. Therefore, under the action of constant load, the model parameters E₂ and ¦Ç₂ tend to decrease.

Figure 9 Freeze-thaw rock fitting verification curve:

Table 4 Elastic and viscous parameters of freeze-thaw rocks

Figure 10 Variation of different freeze-thaw cycles and loading stress model parameters

In the creep of freeze-thaw rock, there is a certain relationship between the deformation characteristics and the loading stress. The existing research results show that there are hardening effect and damage effect in the creep process [43]. According to the variation law of rheological elastic parameter E₂ and viscosity parameter ¦Ç₁ in Table 4, E₂ and ¦Ç₁ exhibit different degrees of attenuation as the loading stress increases. The elastic parameter E₂ decreases sharply at low stress levels but tends to be stable at high stress levels, with a very low variation range. The viscosity parameter decreases with an increase in the stress level. Under the same stress, the viscosity parameter decreases with the increase in the number of freeze-thaw cycles. When the rock is loaded to a high stress level, the hardening effect of the stress on the elastic member is significant, the damage effect is weakened, and the overall performance is characterized by the hardening effect, which causes the elastic parameter to vary in a small range. However, the viscous element has been degraded by damage, and the freezing and thawing effect will accelerate the damage; thus, the rock plasticity will increase. In the physical sense, as the loading increases, the pores and micro-cracks inside the rock are continuously compressed and deformed, and the pore structure is destroyed, which makes the rock bearing capacity decrease and the rock damage effect significant. With the increase in the stress level, the stress limits the damage and deformation of rock particles, the compression deformation and damage degree of rock pores and micro-cracks are weakened, and the hardening effect of rock appears. However, due to the increasing damage degree of rock, the effect of the damage is still present. At the same time, the freeze-thaw cycle accelerates the damage of the pore structure inside the rock, making it more prone to large deformation under the same load, resulting in continuous reduction in the rock long-term strength.

5 Conclusions

In summary, a creep constitutive model of freeze-thaw rock based on the damage element was constructed, and a creep test of freeze-thaw rock was carried out. The accuracy and applicability of the model were verified. The following conclusions were obtained:

1) According to the rock damage mechanics, the freeze-thaw damage factor based on NMR porosity is defined, and the creep aging damage factor based on volume strain, the elastic damage element, and the viscous damage element, which characterize the creep damage characteristics, is obtained. Consequently, based on the existing classical creep combination model, the creep model and constitutive equation of freeze-thaw rock, considering the damage effect, are established.

2) The creep test of freeze-thawed rock was conducted, and the parameters of the frozen-thaw rock creep model were identified. With an increase in the number of freeze-thaw cycles, the rock plastic deformation is determined to be enhanced; the volume increased; the freezing and thawing effect on the rock made significant; and the long-term strength reduced.

3) The analysis of the elastic and viscous parameters of the creep model shows that the damage effect of the rock is significant as the loading stress level increases. However, at a high stress level, the elasticity of rock is hardened to varying degrees, which slows down the damage degradation of rock. In general, the elastic and viscous parameters decrease, and the damage effect appears.

4) The analysis results of the test data show that the physical parameters of the frozen-thaw rock creep model with damage factor are clear, which can better explain the rock damage caused by freeze-thaw cycles, and is suitable for long-term strength and stability analysis of rocks in cold regions.

Contributors

ZHU Long-yin provided the concept and edited the first draft of manuscript. LI Jie-lin conducted the literature review. ZHOU Ke-ping edited the draft of manuscript. CHEN Hui developed the overarching research goals. LIN Yun analyzed the measured data. GAO Le calculated the data. SHEN Yan-jun analyzed the calculated results. All authors replied to reviewers¡¯ comments and revised the final version.

Conflict of interest

LI Jie-lin, ZHU Long-yin, ZHOU Ke-ping, CHEN Hui, GAO Le, LIN Yun, SHEN Yan-jun declare that they have no conflict of interest.

References

[1] MU Yan-hu, MA Wei, NIU Fu-jun, LIU Ge, ZHANG Qing-long. Study on geotechnical hazards to roadway engineering in permafrost regions [J]. Journal of Disaster Prevention and Mitigation Engineering, 2014, 34(3): 259-267. DOI: 10.13409/j.cnki.jdpme.2014.03.005. (in Chinese)

[2] LUI Hui, YANG Geng-she, JIA Hai-liang, YE Wan-jun, WEI Yao, XI Jia-mi, SHEN Yan-jun, ZHANG Hui-mei. Experimental study on meso-structure of rock in the process of crack (pore) water freezing [J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(12): 2516-2524. DOI: 10.13722/j.cnki.jrme.2016.0906. (in Chinese)

[3] AL-OMARI A, BECK K, BRUNETAUD X, AKOS T, MUKHTAR A. Critical degree of saturation: A control factor of freeze-thaw damage of porous limestones at Castle of Chambord, France [J]. Engineering Geology, 2015, 185(3): 71-80. DOI: 10.1016/j.enggeo.2014.11.018.

[4] KHANLARI G, SAHAMIEH R Z, ABDILOR Y. The effect of freeze-thaw cycles on physical and mechanical properties of upper red formation sandstones, central part of Iran [J]. Arabian Journal of Geosciences, 2015, 8(8): 5991-6001. DOI: 10.1007/s12517-014-1653-y.

[5] FENG Fan, LI Xi-bing, JAMAL Rostami, PENG Ding-xiao, LI Di-yuan, DU Kun. Numerical investigation of hard rock strength and fracturing under polyaxial compression based on Mogi-Coulomb failure criterion [J]. International Journal of Geomechanics, 2019, 19(4): 04019005. DOI: 10.1061/ (ASCE)GM.1943-5622.0001352.

[6] CHEN Wei-zhong, TAN Xian-jun, YU Hong-dan, YUAN Ke-kuo, LI Shu-cai. Advance and review on thermo-hydro- mechanical characteristics of rock mass under condition of low temperature and freeze-thaw cycles [J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(7): 1318- 1336. (in Chinese)

[7] HUANG Shi-bing, LIU Quan-sheng, CHENG Ai-ping, LIU Yan-zhang. A statistical damage constitutive model under freeze-thaw and loading for rock and its engineering application [J]. Cold Regions Science and Technology, 2018, 145(1): 142-150. DOI: 10.1016/j.coldregions.2017.10.015.

[8] DAVID G. Creep of rocks [J]. The Journal of Geology, 1939, 47(3): 225-251.

[9] FU Bing-jun. Academician Chen Zongji¡¯s life [J]. Progress in Rock Mechanics and Engineering, 2002, 8(3): 1-9.

[10] TOSHIHISA A, AKIO T. Prediction of long term strength of soft sedimentary rock [C]// Proceedings of the International Symposium on Weak Rock, Tokyo, 1981: 99-104.

[11] ZHAO Bao-yun, LIU Dong-yan, ZHENG Ying-ren, LIU Hong. Uniaxial compressive creep test of red sandstone and its constitutive model [J]. Journal of Mining & Safety Engineering, 2013, 30(5): 744-747. (in Chinese)

[12] ZHAO Yan-lin, ZHANG Lian-yang, WANG Wei-jun, WAN Wen, LI Shu-qing, MA Wen-hao, WANG Yi-xian. Creep behavior of intact and cracked limestone under multi-level loading and unloading cycles [J]. Rock Mechanics and Rock Engineering, 2017, 50(6): 1-16. DOI: 10.1007/s00603-017- 1187-1.

[13] LI Bing. Research on creep properties and damage rupture mechanism of concrete under freeze-thaw effect [D]. Xuzhou: China University of Mining and Technology, 2016. (in Chinese)

[14] KARACA Z, DELIORMANLI A H, ELCI H, PAMUKCU C. Effect of freeze-thaw process on the abrasion loss value of stones [J]. International Journal of Rock Mechanics & Mining Sciences, 2010, 47(7): 1207-1211. DOI: 10.1016/ j.ijrmms.2010.07.003.

[15] ZHOU Zhi-wei, MA Wei, ZHANG Shu-juan, MU Yan-hu, LI Guo-yu. Effect of freeze-thaw cycles in mechanical behaviors of frozen loess [J]. Cold Regions Science and Technology, 2018, 146(2): 9-18. DOI: 10.1016/j.coldregions. 2017.11.011.

[16] WEI Li-de, YANG Chun-he, XU Wei-ya. Study on creep damage constitutive model of salt rock based on mesomechanics [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(23): 4253-4258. (in Chinese)

[17] XIA Cai-chu, JIN Lei, GUO Rui. Nonlinear theoretical rheological model for rock: A review and some problems [J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(3): 454-463. (in Chinese)

[18] LU Ya-ni, LI Xin-ping, CHAN A. Damage constitutive model of single flaw sandstone under freeze-thaw and load [J]. Cold Regions Science and Technology, 2019, 159: 20-28. DOI: 10.1016/j.coldregions.2018.11.017.

[19] KANG Yong-gang, ZHANG Xiu-e. An improved constitutive model for rock creep [J]. Rock and Soil Mechanics, 2014, 35(4): 1049-1055. DOI: 10.16285/j.rsm. 2014.04.011. (in Chinese)

[20] PU Cheng-zhi, CAO Ping, ZHANG Chun-yang, ZHANG Qiu-cai. Variable parameters nonlinear creep damage model of rock with consideration of aging, damage and deterioration [J]. Engineering Mechanics, 2017, 34(6): 17-27. (in Chinese)

[21] SHEN Cai-hua, ZHANG Bing, WANG Wen-wu. A new visco-elastoplastic creep constitutive model based on strain energy theory [J]. Rock and Soil Mechanics, 2014, 5(12): 3430-3436. DOI: 10.16285/j.rsm.2014.12.016. (in Chinese)

[22] CHEN Yuan-jiang, PAN Chang-liang, CAO Ping, WANG Wen-xing. Endochronic rheological constitutive model of soft rock [J]. The Chinese Journal of Nonferrous Metals, 2003, 13(3): 735-742. DOI: 10.19476/j.ysxb.1004.0609. 2003.03.041. (in Chinese)

[23] MOMENI A, ABDILOR Y, KHANLARI G R, HEIDARI M, SEPAHI A A. The effect of freeze-thaw cycles on physical and mechanical properties of granitoid hard rocks [J]. Bulletin of Engineering Geology and the Environment, 2016, 75(4): 1649-1656. DOI: 10.1007/s10064-015-0787-9.

[24] LI Jie-lin, ZHOU Ke-ping, ZHANG Ya-min, XU Yu-juan. Experimental study of rock porous structure damage characteristics under condition of freezing-thawing cycles based on nuclear magnetic resonance technique [J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(6): 1208-1214.

[25] HACHIMI D, NAIMA B, ABDELDJALIL Z. Modeling of creep behavior of an argillaceous rock by numerical homogenization method [J]. Periodica Polytechnica Civil Engineering, 2018, 62(2): 462-469. DOI: 10.3311/ PPci.11697.

[26] BIKONG C, HOXHA D, SHAO J F. A micro-macro model for time-dependent behavior of clayey rocks due to anisotropic propagation of microcracks [J]. International Journal of Plasticity, 2015, 69: 73-88. DOI: 10.1016/ j.ijplas.2015.02.001.

[27] XU Hong-fa. Time dependent behaviours of strength and elasticity modulus of weak rock [J]. Chinese Journal of Rock Mechanics and Engineering, 1997, 16(3): 245-251. (in Chinese)

[28] XU Tao, TANG Chun-an, ZHAO Jian, LI Lian-chong, HEAP M J. Modelling the time- dependent rheological behaviour of heterogeneous brittle rocks [J]. Geophysical Journal International, 2012, 189(3): 1781-1796. DOI: 10.1111/ j.1365-246X.2012.05460.x. (in Chinese)

[29] YANG Zhen-wei, JIN Ai-bing, GAO Yong-tao, WANG Kai, SUN Hao. Non-stationary Nishihara model in the particle flow code [J]. Chinese Journal of Engineering, 2015, 37(7): 831-838. DOI: 10.13374/j.issn2095-9389.2015.07.002. (in Chinese)

[30] HUANG Shi-bing, LIU Quan-sheng , CHENG Ai-ping, LIU Yan-zhang, LIU, Guo-feng. A fully coupled thermo- hydro-mechanical model including the determination of coupling parameters for freezing rock [J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 103: 205-214. DOI: 10.1016/j.ijrmms.2018.01.029.

[31] JIA Hai-liang. Theoretical damage models of porous rocks and hard jointed rocks subjected to frost action and further experimental verifications [D]. Wuhan: China University of Geosciences, 2016. (in Chinese)

[32] XU Qiang, LU Zhong-yu, WANG Xue. Damage modelling: The current state and the latest progress on the development of creep damage constitutive equations for high Cr steels [J]. Materials at High Temperatures, 2017, 34(3): 229-237. DOI: 10.1080/09603409.2017.1289613. (in Chinese)

[33] KONG Xiang-yan. Isopercolation mechanics of pupils [M]. Hefei: China University of Science and Technology Press, 1999. (in Chinese)£Š

[34] KE Bo, ZHOU Ke-ping, XU Chao-shui, DENG Hong-wei, LI Jie-lin, Bin Feng. Dynamic mechanical property deterioration model of sandstone caused by Freeze-thaw weathering [J]. Rock Mechanics and Rock Engineering, 2018, 51(9): 2791-2804. DOI: 10.1007/s00603-018-1495-0. (in Chinese)

[35] WEI Li-de, YANG Chun-he, XU Wei-ya. A damage constitutive model for rock with plastic volume strain [J]. Engineering Mechanics, 2006, 23(1): 139-143. (in Chinese)

[36] LU Jian-guo, WANG Zhi-qiao, LIU Hong-yan. Rock fracture and damage [M]. Beijing: Geological Publishing House, 2013. (in Chinese)

[37] YUAN Xiao-qing, LIU Hong-yan, LIU Jing-ping. A damaging model of jointed rock under coupled action of freezing and thawing [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(8): 1602-1611. DOI: 10.13722/j.cnki.jrme.2014.1342. (in Chinese)

[38] ZHANG Hui-mei, YANG Geng-she. Research on damage model of rock under coupling action of freeze-thaw and load [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(3): 471-476. (in Chinese)

[39] BOURAS Y, DUSAN Z, TEODOR M A, ZORA V. A non-linear thermo-viscoelastic rheological model based on fractional derivatives for high temperature creep in concrete [J]. Applied Mathematical Modelling, 2018, 55: 551-568. DOI: 10.1016/j.apm.2017.11.028.

[40] XIA Cai-chu, JIN Lei, GUO Rui. Nonlinear theoretical rheological model for rock: A review and some problems [J] Chinese Journal of Rock Mechanics and Engineering, 2011, 30(3): 454-463. (in Chinese)

[41] SHAO Jian-fu, ZHU Qi-zhi, SU K. Modeling of creep in rock materials in terms of material degradation [J]. Computers and Geotechnics, 2003, 30(7): 549-555. DOI: 10.1016/S0266-352X(03)00063-6.

[42] XU Wei-ya, YANG Sheng-qi, CHU Wei-jiang. Nonlinear viscoelasto-plastic rheological model (hohal model) of rock and its engineering application [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 433-447. (in Chinese)

[43] SONG Yong-jun, LEI Sheng-you, LIU Xiang-ke. Non-linear rock creep model based on hardening and damage effect [J]. Journal of China Coal Society, 2012, 37(S2): 287-292. (in Chinese)

(Edited by ZHENG Yu-tong)

ÖÐÎĵ¼¶Á

¶³ÈÚÑ­»·ÏÂÉ°ÑҵķÇÏßÐÔÈä±äËðÉËÄ£ÐÍ

ÕªÒª£ºÎªÁËÑо¿¶³ÈÚÑ­»·ÓëÔغɵij¤ÆÚ×÷ÓÃÏÂÑÒʯÄÚ²¿µÄËðÉËÌØÐÔ£¬ÒÔÁ÷±äÀíÂÛ¡¢ËðÉËÁ¦Ñ§Îª»ù´¡£¬¶¨ÒåÁË»ùÓں˴Ź²Õñ¿×϶¶ÈµÄÑÒʯ¶³ÈÚËðÉËÒò×ÓÓë»ùÓÚÌåÓ¦±äµÄÈä±äËðÉËÒò×Ó£¬²¢½«ËðÉËÒò×ÓÒýÈë»ù±¾Á÷±äÔª¼þÖУ¬½¨Á¢Á˶³ÈÚÑÒʯµÄ·ÇÏßÐÔÈä±äËðÉ˱¾¹¹Ä£ÐÍÓë·½³Ì£¬ÓÃÒÔÃèÊö¶³ÈÚÑÒʯÔں㶨ÔغÉϵķÇÏßÐÔÈä±äÌØÕ÷¡£Í¬Ê±£¬¿ªÕ¹Á˶³ÈÚÑÒʯµÄ·Ö¼¶¼ÓÔØÈä±äÊÔÑ飬»ñµÃÁ˶³ÈÚÑ­»·Ç°ºóºË´Å¹²Õñ¿×϶¶ÈÓëÑÒʯºáÏòÓ¦±ä¡¢×ÝÏòÓ¦±äµÄ±ä»¯Çé¿ö¡£ÒÔÊÔÑéÊý¾ÝΪ»ù´¡£¬·ÖÎö²¢ÑéÖ¤Á˶³ÈÚÑÒʯÈä±äËðÉËÄ£Ð͵ÄÊÊÓÃÐÔÓë׼ȷÐÔ¡£½á¹û±íÃ÷£¬ÔÚ¶³ÈÚÑ­»·µÄ×÷ÓÃÏ£¬ÑÒʯÄÚ²¿¿×϶½á¹¹²»¶ÏËðÉËÁÓ»¯£¬ºË´Å¹²Õñ¿×϶¶È³ÖÐøÔö¼Ó£»Ôں㶨ÔغɵÄ×÷ÓÃÏ£¬ÑÒʯµÄËÜÐÔ±äÐÎÔö¼Ó£¬Ìå»ýÔö³¤Ã÷ÏÔ£¬Èä±äʱЧËðÉËÔöÇ¿¡£Ëæ׿ÓÔØÓ¦Á¦µÄÔö¼Ó£¬ÑÒʯµÄ˲ʱµ¯ÐÔ²ÎÊýÔö´ó£¬Á÷±äµ¯ÐÔ²ÎÊý¡¢ð¤ÐÔ²ÎÊýÔÚ¿ìËÙ½µµÍ£»ÆäÖиßÓ¦Á¦Ë®Æ½¶ÔÑÒʯ¾ßÓÐÓ²»¯×÷ÓôӶø¼õÈõ²¿·ÖËðÉËЧӦ£¬Ê¹µÃºóÆÚÁ÷±äµ¯ÐÔ²ÎÊýÔÚС·¶Î§²¨¶¯£¬¶ø¶³ÈÚÑ­»·µÄËðÉËÁÓ»¯×÷Óã¬Ê¹µÃÑÒʯµÄð¤ËÜÐÔ¼õÈõ£¬µ¼ÖÂð¤ÐÔϵÊýËæ×Ŷ³ÈÚ´ÎÊýµÄÔö¼Ó¶ø¿ìËÙ½µµÍ£¬µ«×ÜÌåÉÏÑÒʯ²»¶ÏµÄËðÉËÁÓ»¯£¬³¤ÆÚÇ¿¶È³ÖÐø½µµÍ¡£±¾ÎĽ¨Á¢µÄ»ùÓÚËðÉËÒò×ӵĶ³ÈÚÑÒʯÈä±äÄ£ÐÍ£¬Äܹ»×¼È·ÃèÊö¶³ÈÚÑÒʯµÄ·ÇÏßÐÔÌØÕ÷¡£

¹Ø¼ü´Ê£ºÊ±Ð§Ë𻵣»Èä±äËðÉËÄ£ÐÍ£»ËðÉËÒò×Ó£»Îȶ¨Èä±ä

Foundation item: Projects(41502327, 51474252, 51774323) supported by the National Natural Science Foundation of China; Project(2020JJ4712) supported by the Natural Science Foundation of Hunan Province, China; Project(CX20190221) supported by the Hunan Provincial Innovation Foundation for Postgraduate, China; Project(ZJRMG-2018-Z03) supported by the Key Laboratory of Rock Mechanics and Geohazards of Zhejiang Province, China

Received date: 2020-06-19; Accepted date: 2020-12-07

Corresponding author: LI Jie-lin, PhD, Associate Professor; Tel: +86-13873137080; E-mail: lijielin@163.com; ORCID: https://orcid.org/0000-0003-3677-4561; ZHU Long-yin, Master, Associate Engineer; Tel: +86-18890096519; E-mail: zhulongyin@csu.edu.cn; ORCID: https://orcid.org/0000-0002-5478-5198