J. Cent. South Univ. (2017) 24: 1387-1395
DOI: 10.1007/s11771-017-3543-4
Three-dimensional formation keeping of multi-UAV based on consensus
ZHU Xu(朱旭)1, ZHANG Xun-xun(张逊逊)1, YAN Mao-de(闫茂德)1, QU Yao-hong(屈耀红)2
1. School of Electronic and Control Engineering, Chang’an University, Xi’an 710064, China;
2. School of Automation, Northwestern Polytechnical University, Xi’an 710129, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract: Consensus is an emerging technique using neighbor-to-neighbor interaction to generate steering commands for cooperative control of multiple vehicles. A three-dimensional formation keeping strategy for multiple unmanned aerial vehicles (multi-UAV) is proposed based on consensus, aiming at maintaining a specified geometric configuration. A formation control algorithm with guidance and corresponding flight controllers is given, managing position and attitude, respectively. In order to follow a three-dimensional predefined flight path, by introducing the tracking orders as reference states into the consensus, the formation control algorithm is designed, following the predefined flight path and maintaining geometric configuration simultaneously. The flight controllers are constructed by nonlinear dynamic inverse, including attitude design and velocity design. With the whole system composed of a nonlinear six-degree-of-freedom UAV model, the formation control algorithm and the flight controllers, the formation keeping strategy is closed loop and with full states. In simulation, three-dimensional formation flight demonstrates the feasibility and effectiveness of the proposed strategy.
Key words: multiple unmanned aerial vehicles; formation keeping; consensus; reference state; flight control
1 Introduction
Recently, formation control of multiple unmanned aerial vehicles (multi-UAV) has been an active topic since it promises many practical applications, such as reconnaissance, surveillance, atmospheric study, communication relaying, search and rescue [1, 2]. Some of these tasks may be dangerous and will not be recommended for human pilots, thus making them ideal for autonomous unmanned vehicles.
Some research methods were proposed for multi-UAV control, such as leader-follower [3], behavior based approach [4], virtual structure [5], artificial potential function [6]. As pointed out in Ref. [7], different approaches have their specific benefits and drawbacks in different aspects of formation control problems. For example, the leader-follower approach is easy to implement but has no explicit feedback on formation and lack of robustness due to the existence of the leader, behavior approaches can ensure collision avoidance but are difficult to analyze mathematically, and so on. What’s worse, these methods rarely take into account the communication topology between UAVs that they cannot make full use of information flow and sharing. In order to use the information flow for improving synchronization of the entire formation, consensus has attracted more and more interest of researchers [8]. The consensus algorithms require only neighbor-to-neighbor interaction and carry out the decentralized control strategy, which minimizes power consumption, increases stealth, and improves the scalability and robustness of the formation [9].
Consensus can make the formation evolve as a rigid body in a given direction with some given orientation and maintain the geometric relationship. For more specific formation flight problems of aircraft, consensus means that the vehicles should be able to achieve tracking for given velocity, heading and altitude commands [10]. Even if a UAV is destroyed, other UAVs can still use the remaining neighbor-to-neighbor information to achieve consensus and realize formation control [11]. In a word, consensus has more advantages than traditional formation control algorithms in practice.
Some efforts of consensus have been devoted to UAV formation control. A consensus-based feedback linearization method is proposed to maintain a specified time-varying geometric configuration for formation flight [12]. UAVs with different dynamics are synchronized in the presence of topology variation, providing a rigid geometric configuration, where finite-time consensus collision-avoidance algorithm is designed for both leaderless and leader-follower formation [13]. Multi-UAV arrives at target location simultaneously by consensus seeking with switching and imperfect communication among the vehicles [14]. A testbed is even constructed to validate the consensus algorithm, using a global positioning system [15].
However, most of these existing documents about consensus recognize the UAV as a point mass [16]. Some scholars assume that an automatic pilot operates in the inner-loop and its executive capability is infinite [17]. Both above assumptions are too idealistic to be used in practice. Moreover, the relationship between formation control and flight control is seldom studied.
Therefore, it is of great need to solve these critical problems and advance consensus in formation application. In this work, we focus on formation keeping using consensus to utilize communication information efficiently. A formation control algorithm with guidance and corresponding flight controllers is proposed, where the relationship between them is also demonstrated clearly. With the whole system composed of a nonlinear six-degree-of-freedom UAV model, the formation control algorithm and the flight controllers, the formation keeping strategy based on second-order consensus is closed loop and with full states.
2 Multi-UAV model
2.1 Coordination variables
Consider the formation of n identical UAVs, in which each is denoted by Ui for  eij is a directed edge from Uj to Ui, and Ui can get information comprised of position and velocity from Uj. Define nonnegative adjacency weight aij associated with the edge eij. Moreover, assume aii=0. The set of neighbors for Ui is denoted by Ni.
eij is a directed edge from Uj to Ui, and Ui can get information comprised of position and velocity from Uj. Define nonnegative adjacency weight aij associated with the edge eij. Moreover, assume aii=0. The set of neighbors for Ui is denoted by Ni.
After describing the communication topology, choosing coordination variables becomes another major concern of consensus as consistent coordination variables are the final objective of consensus. Position and velocity coordination variables are selected that velocity Vi can be used as velocity coordination variables directly and position coordination variables should be chosen more complicatedly.
To this end, the definition of position coordination variable will be given. It is defined as a reference ρiF, and the position vector from Ui to its reference point is denoted by  Geometric configuration and position coordination variables are demonstrated as Fig. 1 in both unsteady case and steady case.
Geometric configuration and position coordination variables are demonstrated as Fig. 1 in both unsteady case and steady case.
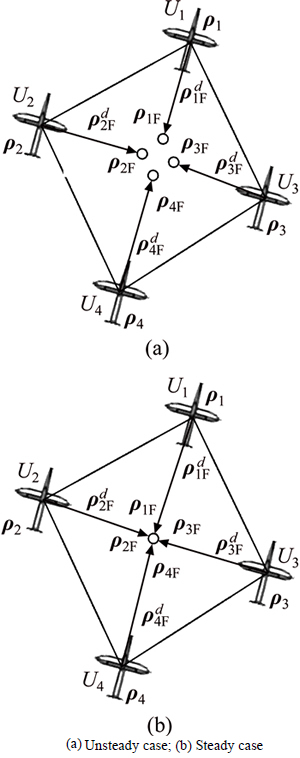
Fig. 1 Position coordination variable of Ui generated by ρiF:
Suppose that the predefined geometric configuration of the formation is known. Position coordination variable is obtained by vector computation:
 (1)
(1)
If  as
as formation keeping is realized.
formation keeping is realized.
2.2 UAV model
Multi-UAV control depends on adjusting position and attitude of each one. Hence, it is necessary to describe the UAV model, which is given by the nonlinear six-degree-of-freedom differential equation:
 (2)
(2)
where is the state of a UAV; Vi is airspeed; αi is attack angle; βi is sideslip angle; pi, qi, ri are roll angular rate, pitch angular rate and yaw angular rate, respectively; fI, θi, ψi are roll angle, pitch angle and yaw angle, respectively; xi, yi, zi are longitudinal, lateral and altitudinal displacement, respectively.
is the state of a UAV; Vi is airspeed; αi is attack angle; βi is sideslip angle; pi, qi, ri are roll angular rate, pitch angular rate and yaw angular rate, respectively; fI, θi, ψi are roll angle, pitch angle and yaw angle, respectively; xi, yi, zi are longitudinal, lateral and altitudinal displacement, respectively.
The actuator represents aileron, rudder, elevator and throttle. The specific form of Eq. (2) is shown as follows [18]:
represents aileron, rudder, elevator and throttle. The specific form of Eq. (2) is shown as follows [18]:
 (3)
(3)
 (4)
(4)
 (5)
(5)
 (6)
(6)
where m is mass of a UAV; g is gravity coefficient;  Mi, Ni are rolling moment, pitching moment and yawing moment, respectively; ui, vi, wi are velocity components along body coordinate axes, and the definition of other parameters can be found in Ref. [18].
Mi, Ni are rolling moment, pitching moment and yawing moment, respectively; ui, vi, wi are velocity components along body coordinate axes, and the definition of other parameters can be found in Ref. [18].
To describe the control accuracy of the formation control, position errors, exi, eyi, ezi are defined by their corresponding coordination variables. For simplicity, x channel is chosen to be as a representative.
 (7)
(7)
The errors for y, z channels are defined in the same way.
The error of the state in Eq. (2) is defined as follows:
 (8)
(8)
where ci is a positive constant less than 1. Equations (7) and (8) incorporate error information from different UAVs in the system, to identify the performance of the formation.
3 Formation control
Multi-UAV formation keeping mainly depends on the formation control system, which can also utilize tracking control orders to follow the predefined flight path. According to the coordination variables of other UAVs and the tracking control orders, the formation control orders are generated to achieve formation keeping and make the formation fly along the predefined flight path. The formation control system transmits the formation control orders to the flight control system, which adjusts attitude to follow these orders. The structure of multi-UAV formation keeping is depicted in Fig. 2.
3.1 Formation keeping based on consensus
A second-order consensus algorithm is adopted to design the formation keeping algorithm. Longitudinal, altitudinal and lateral channels are designed respectively as
 (9)
(9)
where γ is a positive constant greater than 1, and  is the relative speed of Uj to Ui:
is the relative speed of Uj to Ui:
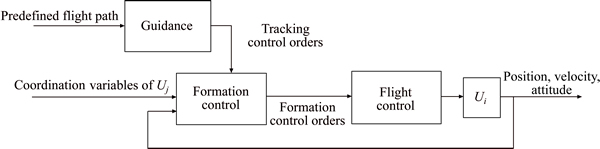
Fig. 2 Structure of multi-UAV formation keeping
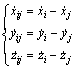
Once the three desired accelerations in Eq. (9) in the ground coordinate system are given, formation keeping can be achieved. Though ρiF is different from each other in the beginning, formation keeping is achieved if  as
as  To further design the formation keeping algorithm based on consensus, the desired accelerations in Eq. (9) are transformed into a set of real orders
To further design the formation keeping algorithm based on consensus, the desired accelerations in Eq. (9) are transformed into a set of real orders  as follows:
as follows:
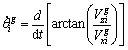
 (10)
(10)
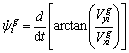
 (11)
(11)
 (12)
(12)
where  are the desired pitch, yaw and velocity. Equations (10)-(12) are the orders for formation keeping based on the second consensus.
are the desired pitch, yaw and velocity. Equations (10)-(12) are the orders for formation keeping based on the second consensus.
3.2 Formation control with guidance
To follow a predefined flight path, the formation control algorithm composed of vertical, flat and velocity guidance laws is proposed to provide formation control orders. More particularly, the tracking control orders are treated as reference states and introduced into consensus to determine the stable states of the formation control algorithm.
3.2.1 Vertical guidance law
The vertical tracking order for pitch is designed as [19]
 (13)
(13)
where  are the proportional, integral and differential coefficients, respectively; Δzi is the vertical track error, which is positive above the predefined altitude and negative below;
are the proportional, integral and differential coefficients, respectively; Δzi is the vertical track error, which is positive above the predefined altitude and negative below;  can be recognized as a reference state. Based on Eqs. (10) and (13), the vertical guidance law in terms of pitch order
can be recognized as a reference state. Based on Eqs. (10) and (13), the vertical guidance law in terms of pitch order  is obtained.
is obtained.
 (14)
(14)
As a reference state,  determines that there exists
determines that there exists  as time going on [20]. Using Eq. (14), the formation can approach the predefined altitude and reach consensus of pitches.
as time going on [20]. Using Eq. (14), the formation can approach the predefined altitude and reach consensus of pitches.
3.2.2 Flat guidance law
There are two kinds of predefined flight paths for flat guidance, which are straight line and circle. For straight line, ψ0 is the course angle between the initial waypoint and the terminal waypoint. The cross track error is defined as Δdi, which is positive on the right side of the predefined flight path and negative on the left. For straight circle,  is the base heading while the formation initially enters the predefined circular flight path, and Ri is the radius.
is the base heading while the formation initially enters the predefined circular flight path, and Ri is the radius.
The flat tracking order for yaw is given by [19]
 (15)
(15)
where  are the proportional, integral and differential coefficients, respectively. If the formation flies along clockwise circle, the plus-minus sign in the second equation takes plus; otherwise, minus.
are the proportional, integral and differential coefficients, respectively. If the formation flies along clockwise circle, the plus-minus sign in the second equation takes plus; otherwise, minus.
 can be recognized as a reference state. Based on Eqs. (11) and (15), the flat guidance law in terms of yaw order
can be recognized as a reference state. Based on Eqs. (11) and (15), the flat guidance law in terms of yaw order  is obtained.
is obtained.
 (16)
(16)
Turn maneuver can be treated as part of a circle with time-variant radius and it will not be demonstrated.
3.2.3 Velocity guidance law
Suppose that the predefined velocity of the formation is  It is introduced into velocity consensus Eq. (12) to obtain the velocity guidance law in terms of velocity order
It is introduced into velocity consensus Eq. (12) to obtain the velocity guidance law in terms of velocity order 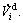
 (17)
(17)
where  is the reference velocity of Ui and it is classified into three types.
is the reference velocity of Ui and it is classified into three types.
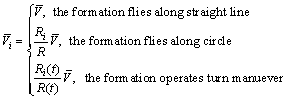
where Ri is the circling radius of Ui and R is the circling radius of the formation. There is no consistent radius for each UAV that UAVs in the outer ring fly with large radius and UAVs in the inner ring fly with small radius.
 is a fixed reference state, which represents the predefined average airspeed of the formation. However, for a single UAV,
is a fixed reference state, which represents the predefined average airspeed of the formation. However, for a single UAV,  is not constant and discussed in three situations. First, when the formation flies along straight line,
is not constant and discussed in three situations. First, when the formation flies along straight line,  is same for each UAV. Second, when the formation flies along circle,
is same for each UAV. Second, when the formation flies along circle,  is large for the UAVs in the outer ring and is small in the inner ring. Third, for turn maneuver,
is large for the UAVs in the outer ring and is small in the inner ring. Third, for turn maneuver,  is similar to circle while it is time variant. Using controller Eq. (17), not only velocity stability is realized, but also
is similar to circle while it is time variant. Using controller Eq. (17), not only velocity stability is realized, but also  as
as  Furthermore, position consensus is also realized by velocity consensus.
Furthermore, position consensus is also realized by velocity consensus.
Overall, Eqs. (14), (16), (17) constitute the formation control algorithm with guidance, which can both achieve formation keeping and make the formation fly along the predefined flight path.
4 Flight control based on nonlinear dynamic inverse
To follow the formation control orders and compensate the nonlinearity of the system, a method for constructing the flight control system is suggested, which is based on nonlinear dynamic inverse. The structure of the flight control algorithm is depicted in Fig. 3.
Nonlinear dynamic inverse design consists of attitude design and velocity design. Attitude design is divided into two loops, where the inner-loop controls angular rates and the outer-loop controls attitude angles.Velocity design is completed by only one loop.
4.1 Designing dynamic inverse controller for attitude in inner-loop
Angular rates of state Eq. (5) can be partly written into affine equation form:
 (18)
(18)
where 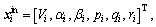
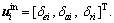
 are deduced as
are deduced as
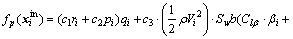
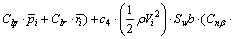
 (19)
(19)
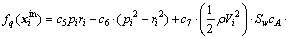
 (20)
(20)
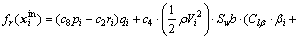
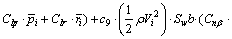
 (21)
(21)
Then,  is computed by
is computed by
 (22)
(22)

Fig. 3 Structure of flight control algorithm
The left side of Eq. (18) is demonstrated as
 (23)
(23)
where are bandwidths of these three channels;
are bandwidths of these three channels; are the desired angular rates generated by the controller in the outer loop.
are the desired angular rates generated by the controller in the outer loop.
Using Eqs. (18)-(23), the dynamic controller for attitude in the inner-loop is obtained.
 (24)
(24)
where  is the Moore-Penrose inverse matrix of
is the Moore-Penrose inverse matrix of 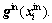
4.2 Designing dynamic controller for attitude in outer-loop
The outer-loop controls attitude angles and its outputs are the inputs of the inner-loop. Attitude angles of state Eq. (4) are partly written into affine equation form:
 (25)
(25)
where 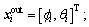
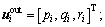
 is computed by
is computed by
 (26)
(26)
Let the left side of Eq. (25) be
 (27)
(27)
Using Eqs. (25)-(27), the dynamic controller for attitude in the outer-loop is obtained.
 (28)
(28)
where  is the Moore-Penrose inverse matrix of
is the Moore-Penrose inverse matrix of  .
.
4.3 Designing dynamic controller for velocity
State Eq. (3) is also partly written into affine equation form:
 (29)
(29)
where  and
and  It is obtained that
It is obtained that
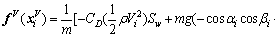
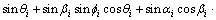
 (30)
(30)
 (31)
(31)
Let  and
and  be defined as Eq. (12). Using Eqs. (29)-(31), the dynamic controller for velocity is obtained.
be defined as Eq. (12). Using Eqs. (29)-(31), the dynamic controller for velocity is obtained.
 (32)
(32)
where  is the Moore-Penrose inverse matrix of
is the Moore-Penrose inverse matrix of 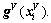
So far, the nonlinear dynamic controllers are designed as Eqs. (24), (28), (32), and they construct the flight control algorithm.
5 Simulation
Simulations are performed for the formation control laws Eqs. (14), (16), (17) and the nonlinear dynamic controllers Eqs. (24), (28), (32). Formation keeping is simulated by using a nonlinear six-degree-of-freedom fixed-wing model of UAVs with a maximum velocity 47 m/s. Three aircrafts are taken for our simulation, where all UAVs are considered similar. Simulation time is 1000 s and operation step is 0.2 s. Figrue 4 shows the communication network, where an edge from Uj to Ui means that Ui can receive information from Uj.
All three UAVs have to maintain an equilateral triangular formation, with side length of 4 m. They do not fly at an identical altitude that U2 and U3 maneuver 4 m lower than U1. However, the team does not start at the desired positions in the beginning that distances among the team are dozens of meters and headings of the UAVs are different from each other. Formation errors are defined as Eqs. (7), (8) and c=0.2.
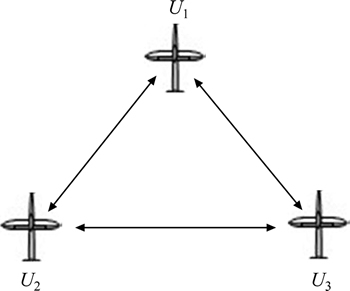
Fig. 4 Communication topology of formation
Define a predefined flight path composed of three waypoints A(0,0,100) m, B(9600,6400,500) m and C(0,6400,400) m. The predefined flight path is arranged as  firstly, and afterwards the formation is required to circle counterclockwise around A with the radius of 1000 m. Straight line, circle and turn are all embodied in the predefined flight path, while planar and vertical position changes are both considered. The reference velocity
firstly, and afterwards the formation is required to circle counterclockwise around A with the radius of 1000 m. Straight line, circle and turn are all embodied in the predefined flight path, while planar and vertical position changes are both considered. The reference velocity  is selected as 39 m/s, and other initial parameters of each UAV are given in Table 1.
is selected as 39 m/s, and other initial parameters of each UAV are given in Table 1.
Table 1 Initial parameters of each UAV

Figure 5 illustrates position and attitude of the team, and Fig. 6 depicts formation errors. From Fig. 5, it can be seen that though position and attitude of the team do not satisfy the desired request in the beginning, under the impact of the formation control laws and the nonlinear dynamic controllers, the team achieves formation keeping in 600 s.
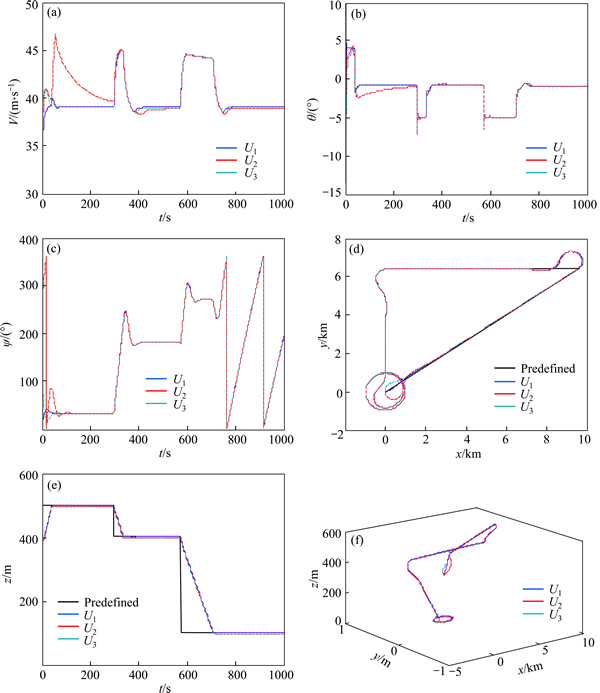
Fig. 5 Position and attitude of formation
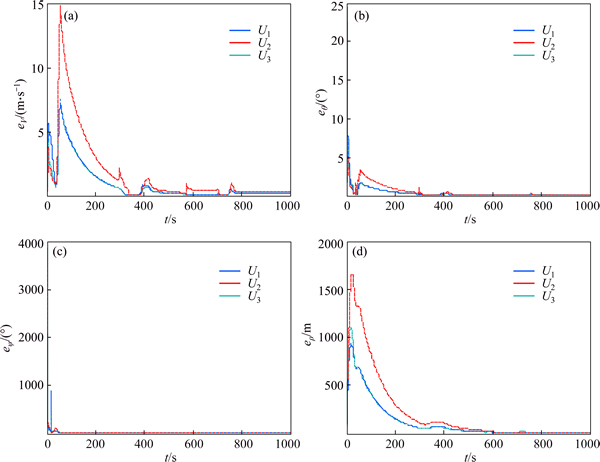
Fig. 6 Position and attitude errors of formation
Figure 5 shows velocity, pitch, heading, planar position, vertical position and three-dimensional position, respectively. In Figs. 5(d) and (e), the dotted line represents the predefined flight path. During the first 300 s, U3 pursues other two UAVs with high speed. At 600 s, the team begins to achieve formation keeping and reach steady state. Afterwards, the formation maintains good geometric configuration whether in turn or in circling. In the second lap of counterclockwise circling, the team tracks the predefined circular path steadily. As can be seen in Fig. 5(f), three-dimensional position composed of Figs. 5(d) and (e) is depicted clearly.
Figure 6 shows errors of velocity, pitch, heading and three-dimensional position, respectively. The errors decrease and approach to 0 within 600 s, which is coincident with position and attitude curves. Control efforts of the formation, such as the maximum value, steady state and stabilization time, are depicted in Table 2.
As a result, simulation result shows that the formation control laws Eqs. (14), (16), (17) and the nonlinear dynamic controllers Eqs. (24), (28), (32) are good at formation keeping and tracking control. Nevertheless, control efforts are not well during turns, including the switch from a straight line to another straight line or a circle, which can be found from every error curve.
Table 2 Control efforts of formation

6 Conclusions
Focusing on multiple unmanned aerial vehicles formation keeping strategy, based on second-order consensus, a formation control algorithm with guidance and corresponding nonlinear dynamic controllers are proposed. By introducing the tracking control orders as reference states into consensus, vertical, flat and velocity formation control laws are given, respectively. To investigate and validate that the proposed strategy is effective and efficient, it is implemented in a nonlinear six-degree-of-freedom fixed-wing model for three UAVs. The simulation results show that the formation can successfully maintain geometric configuration and simultaneously follow the predefined flight path, whether the predefined flight path is straight or circular. Control effort of each UAV has quick response and high control precision.
To further improve the formation keeping strategy and application of consensus, the capability of formation keeping during turn maneuver should be enhanced in the future.
References
[1] KIM S, KIM Y. Trajectory optimization for unmanned aerial vehicle formation reconfiguration [J]. Engineering Optimization, 2014, 46(1): 84-106.
[2] SHI Xiao-hang, LIANG Qing-yang, ZHANG Qin-jie, WANG Jun- sheng, SHEN Xi-qiang. Multi-UAV target tracking using DC-IMM estimate method [J]. Journal of Central South University: Science and Technology, 2013, 44(2): 52-57. (in Chinese)
[3] SASKA M, VONSEK V, KRAJNK T, PEUIL L. Coordination and navigation of heterogeneous MAV-UGV formations localized by a 'hawk-eye'-like approach under a model predictive control scheme [J]. International Journal of Robotics Research, 2014, 33(10): 1393-1412.
[4] DUAN Hai-bin, QIAO Pei-xin. Pigeon-inspired optimization: A new swarm intelligence optimizer for air robot path planning [J]. International Journal of Intelligent Computing and Cybernetics, 2014, 7(1): 24-37.
[5] BAYEZIT I, FIDAN B. Distributed cohesive motion control of flight vehicle formations [J]. IEEE Transactions on Industrial Electronics, 2013, 60(12): 5763-5772.
[6] HOLT J, BIAZ S, YILMAZ L, AJI C A. A symbiotic simulation architecture for evaluating UAVs collision avoidance techniques [J]. Journal of Simulation, 2014, 8(1): 64-75.
[7] SPERANDIO G, PAULO A, HEMERLY E M. Reconfiguration between longitudinal and circular formations for multi-UAV systems by using segments [J]. Journal of Intelligent and Robotic Systems: Theory and Applications, 2015, 78(2): 339-355.
[8] DONG Xi-wang, YU Bo-cheng, SHI Zong-ying, ZHONG Yi-sheng. Time-varying formation control for unmanned aerial vehicles: Theories and applications [J]. IEEE Transactions on Control Systems Technology, 2015, 23(1): 340-348.
[9] YAN Ding, CHEN Wei, BAO Shu-yu. Decentralized formation control for multiple UAVs based on leader-following consensus with time-varying delays [C]// Chinese Automation Congress. Piscataway, United States: IEEE Computer Society, 2013: 426-431.
[10] SUN Tao, XIN Ming. Multiple UAV target tracking using consensus-based distributed high degree cubature information filter [C]// AIAA Guidance, Navigation, and Control Conference. 2015: 1-11.
[11] ZHU Xu, ZHANG Xun-xun, YOU Jin-yu, YAN Mao-de, QU Yao-hong. Swarm control of UAV close formation based on information consensus [J]. Acta Aeronautica et Astronautica Sinica, 2008, 36(12): 3919-3929. (in Chinese)
[12] SEO J, AHN C, KIM Y. Controller design for UAV formation flight using consensus based decentralized approach [C]// AIAA Infotech at Aerospace Conference and Exhibit and AIAA Unmanned Unlimited Conference. Reston: American Institute of Aeronautics and Astronautics Inc, 2009: 1-11.
[13] REIHANE R, FARZANEH A, KARO N. Time-varying formation control of a collaborative heterogeneous multi agent system [J]. Robotics and Autonomous Systems, 2014, 62(12): 1799-1805.
[14] MANATHARA J G, GHOSE D. Rendezvous of multiple UAVs with collision avoidance using consensus [J]. Journal of Aerospace Engineering, 2012, 25(4): 480-489.
[15] JAIMES B, ALDO S, JAMSHIDI M. Consensus-based and network control of UAVs [C]// International Conference on System of Systems Engineering. Piscataway, United States: Institute of Electrical and Electronics Engineers, 2010: 1-6.
[16] WANG Jin-yun, WEI Rui-xuan, DONG Zhi-xing, ZHOU Wei. Research on formation flight control of cooperative UAV [J]. Fire Control Command Control, 2010, 35(3): 34-38. (in Chinese)
[17] BAI Chen, DUAN Hai-bin, LI Chun, ZHANG Yun-peng. Dynamic multi-UAVs formation reconfiguration based on hybrid diversity- PSO and time optimal control [C]// Proceedings of the IEEE Intelligent Vehicles Symposium. Piscataway, United States: Institute of Electrical and Electronics Engineers, 2009: 775-779.
[18] WU Seng-tang, FEI Yu-hua. Flight control system [M]. 2nd ed. Beijing: Beihang University Press, 2006: 9-60.
[19] ZENG Yu. Navigation control system of UAV[D]. Xi’an: School of Automation, Northwestern Polytechnical University, 2009. (in Chinese)
[20] REN Wei, BEARD R W. Distributed consensus in multi–vehicle cooperative control: theory and applications [M]. 1st ed. New York: Springer Publishing Company, 2007: 36-87.
(Edited by YANG Hua)
Cite this article as: ZHU Xu, ZHANG Xun-xun, YAN Mao-de, QU Yao-hong. Three-dimensional formation keeping of multi-UAV based on consensus [J]. Journal of Central South University, 2017, 24(6): 1387-1395. DOI: 10.1007/s11771-017-3543-4.
Foundation item: Project(61473229) supported by the National Natural Science Foundation of China; Projects(310832163403, 310832161012) supported by the Special Fund for Basic Scientific Research of Central Colleges, Chang’an University, China; Project(CXY1512-3) supported by the Xi’an Science and Technology Plan, China
Received date: 2015-11-27; Accepted date: 2016-03-17
Corresponding author: ZHU Xu, Lecturer; Tel: +86-29-82334369; E-mail: zhuxu_1987@sina.com