文章编号:1004-0609(2008)12-2178-07
数值模拟外转角半径及背压对纯钛ECAP变形的影响
李继忠,丁 桦,赵文娟,陈彦博
(东北大学 材料与冶金学院,沈阳 110004)
摘 要:使用DEFORM-3D软件模拟等通道转角挤压过程中外转角半径及背压对纯钛应力和应变分布的影响,探讨不同 R值对材料流动的影响规律。结果显示:当R = 6 mm时,工件上下表面应力状况较为平衡,从而得到均匀的等效应变分布;当R<6 mm时,在外转角形成的死区使材料之间相互搓动,导致工件底部区域出现剧烈畸变,工件不同区域之间的等效应变量差别较大;当R>6 mm时,工件上表面与模具内转角之间的相互作用力增加,使工件顶部变形加剧并导致工件等效应变量不均匀;施加背压(pb)后,能有效提高等效应变量;适当的R值与pb匹配可使工件得到均匀的应变分布。
关键词:等通道转角挤压;外转角半径;数值模拟;背压;纯钛
中图分类号:TG386.1 文献标识码:A
Simulations of influence of outer angular radius and back pressure on ECAP of pure titanium
LI Ji-zhong, DING Hua, ZHAO Wen-juan, CHEN Yan-bo
(School of Materials and Metallurgy, Northeastern University, Shanyang 110004, China)
Abstract: The strain and stress distributions of pure Ti during equal channel angular pressing (ECAP) were simulated by using software of DEFORM-3D with different angular radii and black pressures. The simulated results indicate that the friction forces in the upper and bottom regions can be balanced and the homogeneous equivalent strain distribution can be obtained when R=6 mm. When R<6 mm, the equivalent strain is non-uniform at the bottom of the workpiece, because the death zone makes the materials interact each other, thus induces the bottom of workpiece acutely distorted and makes the value of equivalent strain vary obviously in different regions of workpiece. At R>6 mm, the friction force interacts between the upper face of workpiece and inner corner angular of die, which makes the upper of the workpiece deform remarkably and induces non-uniform equivalent strain distribution. The back pressure can increase the value of equivalent strain. Besides, uniform strain distribution can also be obtained by adopting reasonable back pressure and outer angular radius.
Key words: equal channel angular pressing; outer angular radius; numerical simulation; back pressure; pure titanium
等通道转角挤压(Equal channel angular pressing, ECAP)是SEGAL等[1]是20世纪80年代提出的一种制备超细晶纳米材料的加工方法。因采用该方法可制备出大块体超细晶或纳米晶金属材料,使该加工方法受越来越多科研人员的关注[2?4]。
ECAP挤压过程中,工件变形不均匀一直是影响材料性能的主要原因之一[5?6],许多学者对这方面进行了大量研究。结果表明,这主要是受摩擦力影响,材料在外转角形成死区,导致不同区域材料流动应力相差较大,使工件应变分布不均[7?8]。死区最早是通过模拟发现的[9],后来SHAN等[10]、WU和BAKER[11]通过实验证实了死区的存在。
死区是导致工件变形不均匀的主要因素[12],为消除死区,通常把模具外转角加工成过渡半径,即R值。但是,这样就存在一个问题:过渡半径的存在使工件挤压后形变量降低,削弱了该工艺的意义。为了既能得到均匀的应变分布,又不降低工件形变量,在工件出口端施加背压,可有效提高工件的变形量[13]。但是在实际挤压过程中发现,背压过大使挤压过程困难,对应变分布也没有明显改善。这就需要选择适当的背压,既能得到提高工件的形变量,又能使挤压顺利进行。目前主要通过模拟分析[6?7, 14?15]验证了变形不均匀与模具结构尺寸有密切关系,但都没有给出具体的解决方案。另外,背压在挤压过程中对材料流动的影响比较复杂,有待进一步研究。
本文作者使用大型商业有限元软件DEFORM-3D模拟不同模具外转角半径R值和背压对工件变形行为的影响,分析背压及R值对应力、应变分布的影响规律,探讨R与背压之间的密切关系,选取合适的背压,优化ECAP挤压过程。
1 参数设定及模拟过程条件
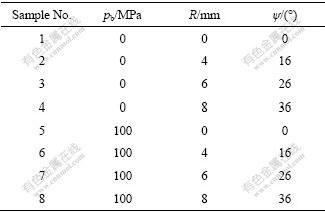
在实际加工过程中,由于模具变形量很小,对材料变过程影响很小,在实际操作过程中,将模具设定为刚性材料,在挤压过程中,同时对模具和工件进行加热和保温,使工件在恒温条件下挤压,因此,假设工件和模具间没有热交换作用。挤压通道截面尺寸为16 mm×16 mm,工件的尺寸为16 mm×16 mm×100 mm。假定工件与模具之间没有热交换作用,工件温度恒定不变。内转角Φ = 90?不变,内转角半径r=0,外转角半径(R)、背压(pb)以及与R值对应的外转角ψ值如表1所列。
表1 模拟的过程设定参数值
Table 1 Parameters in simulations
工件材料选用纯钛,挤压温度为450 ℃,挤压锤头速度v=1.5 mm/s。由于工件形变量较大,为得到精确模拟结果,设定当工件相对变形量大于0.8时,系统自动重新划分网格,以防止网格畸变造成的影响;为便于与其他文献比较,本模拟选取摩擦因数f=0.35,将工件自由离散成40 000个四面体单元,共6 967个节点,工件表面共7 796个多边形。
2 结果与讨论
为便于比较背压及R值对工件等效应变分布的影响,在挤压后的工件中取横截面分析等效应变分布。将该横截面分成Ⅰ、Ⅱ和Ⅲ共3个区域,如图1(a)所示。Ⅰ区距上表面5 mm范围内,Ⅱ区距上表面5~11 mm之间的区域,Ⅲ区距底部5 mm范围内。图1(b)所示为该截面上3条AA′、BB′、CC′线分别表示工件横截面左侧、中间和右侧,其中AA′距左表面2 mm,BB′为工件中线,CC′距右表面2 mm。

图1 工件横截面标定示意图
Fig.1 Schematic diagrams of different regions of workpiece in cross-section: (a) Zone plane; (b) Orientation line
2.1 R值对材料在转角变形区变形行为的影响
在挤压过程中,工件底部与模具之间摩擦力的相互作用较为剧烈,从而在模具外转角处产生死区。在摩擦因数较小的情况下,材料流动受摩擦阻力较小,在模具外转角处有部分未被填充的空隙;当摩擦因数较大时,随着摩擦力增大,使工件底部材料流动阻力增加,外转角处的空隙被材料填充,形成死区。 如图2(a)所示,当R=0时,部分材料受摩擦力作用滞留在外转角处,与流经转角的材料之间发生相互搓动,这部分变形区称为粘滞带。
工件在通过转角时受粘滞带与剪切带的共同作用发生复杂的变形行为,从图2(a)中可以看出在转角处形成的粘滞带与剪切带相互垂直,并且粘滞带材料之间相互搓动而产生的应力与剪切带形成的剪切应力大小相当。两变形带之间的相互作用严重影响工件等效应变量分布的均匀性,使Ⅲ区形变量明显高于其他区域。在图2(b)中,把模具外转角加工成有一定半径的过渡区域,这样能有效防止材料在外转角因滞留而形成的死区。同时,因死区而形成的粘滞带也消失,工件在转角变形区只发生理想的剪切变形。通过把外转角加工成过渡半径,能有效消除因死区而导致的等效应变分布不均匀现象。在实际实验过程中,通常使用MoS2作润滑剂,以降低工件与模具之间的摩擦力。但是摩擦力不可能完全消除,需要通过改变模具形状来削弱摩擦力的不利影响。

图2 等效应力在转角的分布
Fig.2 Distributions of equivalent stress in die corner: (a) R = 0 mm; (b) R = 6 mm
2.2 R值对工件纵截面等效应变分布的影响
从图3(a)所示,pb = 0 MPa时,在工件Ⅰ区的等效应变量只有1.15左右,而Ⅲ区的等效应变量超过2.0。施加背压pb = 100 MPa后,不均匀的现象并未得到明显改善,由于转角死区的影响,在工件纵截面上几乎没有均匀的变形区域。

图3 不同背压和R值下工件纵截面上等效应变分布
Fig.3 Distribution of equivalent strain in longitudinal section with different outer angular radii and backpressures: (a) R = 0; (b) pb = 0 MPa; (c) pb = 100 MPa
由图3(b)可见,随R值增加,工件的等效应变量逐渐减小,底部剧烈变形减弱。R = 4 mm时,Ⅲ区受粘滞区搓动变形的影响明显降低,等效应变量也由R = 0时的2.0以上降低到1.6左右,但是在靠近外转角的Ⅲ区仍有部分较大的不均匀变形区存在,影响工件变形分布的均匀性。从工件纵截面来看,Ⅲ区受摩擦力的影响,均匀的等效应变区域非常有限,除去头尾变形不均匀区,均匀变形区约占工件总体的30%。当R = 6 mm时,工件同一横截面的上下部区域等效应变量基本相同,且工件纵截面上的均匀等效应变区达45%。R值继续增加到 8 mm时,工件Ⅰ区的等效应变量则出现比Ⅲ区大的现象,这主要是由工件上表面与模具内间的相互作用增大而致,纵截面的均匀等效应变区域相应减小到20%左右。
图3(c)所示为施加背压pb = 100 MPa后,不同外转角半径对等效应变量分布图的影响。当R = 4 mm时,工件底部摩擦力影响仍然比较明显,在过渡区附近仍存在变形量较大的区域,此时等效应变区约为30%,与不施加背压时相比没有明显变化。当R = 6 mm时,在外转角处的死区基本消除,剪切带与出口方向呈45?的理想剪切方向,同时均匀变形区占整体工件的55%,比不施加背压时提高10%。继续增加R值,当R = 8 mm时,在工件转角处顶部开始出现不均匀变形区,使工件的不均匀区增加,均匀区域也只有30%左右。
材料在外转角处的受力情况如图4所示。由图4可知,不同R值直接影响工件上下表面与模具壁之间的接触情况。R值较小时,过渡区较小,锤头压力F直接作用于工件下表面,Ⅲ区畸变虽有所减轻,但还是不能完全消除等效应变不均匀的现象,同时存在部分剧烈变形区,如图3(b)中R = 4所示。当R过大时,过渡区增加,锤头压力Fr而产生的反作用力在Y轴方向的分量Fry作用于内转角,使工件上表面与模具壁之间相互作用加剧,因此,工件Ⅰ区的等效应变量大于Ⅲ区的,如图3(b)R = 8 mm所示。适当的R值既能削弱锤头压力对Ⅲ区下表面剧烈变形的影响,又能使过渡区产生的反作用力分量Fry不足以对内转角压力过大,有效平衡上下表面受力状况,得到均匀的等效应变分布,如图3(b)R = 6 mm所示。

图4 材料在外转角受力示意图
Fig.4 Schematic diagram of material stress at corner
施加背压后,反作用力Fr在X轴方向的分量Frx部分被削弱,同时Fry分量增加,即作用在内转角的力增加。在内转角出现较大的变形,Ⅰ区的等效应变量也明显呈增加的趋势,如图3(c)中R = 6所示。此前,本文作者曾模拟不同摩擦系数施加不同背压时工件等效应变的分布状况,在R = 0、f = 0.35条件下,施加的背压pb = 225 MPa也只能得到较小的等效应变分布区,再增大背压对应变分布影响不大,并且使挤压难以进行,这说明背压不是越大越好。施加背压后,外转角的死区也随之改变,通过调整R值的大小来平衡工件上下表明的受力大小,以便得到均匀的变形区域。本实验中当R = 6 mm时,选取施加pb = 100 MPa是合理的,可获得最大的均匀变形区域(约55%的均匀变 形区)。
2.3 R值对工件横截面等效应变分布的影响
如图5(a)、(c)和(e)所示,当R = 0、pb = 0 MPa时,工件上下区域等效应变量差值较大,最大等效应变量出现在工件Ⅲ区,达1.65以上。而Ⅰ区的等效应变量只有1.25左右,同一横截面上的等效应变量值相差约0.4,变形不均匀区主要集中在工件Ⅲ区两侧,中间较均匀,如图5(a)和(e)所示。当R = 4 mm时,工件整体的等效应变量略降低,横截面上等效应变量差减小到0.2左右,但Ⅲ区的等效应变量仍大于Ⅰ区,死区没有完全消除。当R=6 mm时,横截面上的等效应变量相差不超过0.05,等效应变分布较为理想,死区完全消失。当R = 8 mm时,Ⅲ区的等效应变量则比Ⅰ区的低0.1左右,出现Ⅰ区的等效应变量大于Ⅲ区的现象,过渡区的反作用力对内转角作用明显。图5(b)、(d)和(f)所示为背压pb = 100 MPa时,与不施加背压相比,当R=0时,等效应变分布影响无明显变化。当R = 4 mm时,背压削弱摩擦力的不利影响,使工件Ⅲ区等效应变量降低,使差值也降低到0.05左右。当R = 6 mm时,横截面上的等效应变量分布几乎完全一致,均匀性非常好,同时工件整体的等效应变量也增加0.1左右。当R = 8 mm时,工件Ⅰ区等效应变量仍大于底部,与不施加背压时相比均匀性没有明显改善。从图5可以看出,当R = 6 mm,无论是否施加背压,工件同一横截面上均能得到较好的等效应变分布,工件中间和两侧等效应变分布趋于一致。

图5 不同R值及施加背压对上、下部区域等效应变分布的影响
Fig.5 Distributions of equivalent strain of cross-section under different outer angular radii and back pressures: (a), (c), (e) pb =0 MPa, (b), (d), (f) pb = 100 MPa; (a), (b) AA′ line; (c), (d) BB′ line; (e), (f) CC′ line
比较图5所示的pb = 0 MPa与pb = 100 MPa的等效应变可知:施加背压后对应不同R值等效应变量均匀性有不同程度增加,背压与R值匹配可有效改善工件的整体等效应变分布,使工件上下区的形变量更均匀。同时,从图5中还可以看出随着R值的增加,曲线坡度逐渐减小。施加背压后,背压使曲线坡度进一步减小,在提高Ⅰ区等效应变量的同时,降低Ⅲ区等效应变量,工件等效应变量分布的均匀性更好,同时也提高工件整体的等效应变量。与图3比较可知:当R = 6 mm,不施加背压时能很好地平衡等效应变分布,施加背压后,虽然对横截面上的等效应变量影响不明显,但均匀变形区所占比例明显增加,从45%增加到55%。
2.4 R值对工件Ⅲ区应变速率的影响
如图6所示,当未施加背压时(见图6(a)),Ⅲ区的应变速率随外转角半径的增加而降低,从R = 0时的0.2降低到R = 8 mm时的0.075。施加背压后(见图6(b)),应变速率的大小没有明显改变,但看出曲线均略微展宽,说明材料经过剪切带的时间变长,受剪切力作用加剧,能够累积更多的变形增加等效应变量,此外,从图6(a)和(b)也能看出,当R<6 mm时死区没有完全消除,R = 4 mm与R = 0时等效应变速率没有明显变化,死区对工件Ⅲ区的影响仍占主导作用。当R≥6 mm时,等效应变速率明显降低,导致Ⅲ区的变形量相应减小,从而使材料Ⅲ区应变量相应减小,使工件整体变形量均匀。可以推断:当R = 6 mm时外转角死区完全消除,去除了因死区而产生的变形不均匀现象。但是,R值过大会使应变速率进一步降低,使工件Ⅲ区等效变形量继续减小,开始出现Ⅰ区变形大于Ⅲ区的不均匀现象,这也是不希望得到的结果。

图6 不同背压和R值下工件Ⅲ区的应变速率分布
Fig.6 Distributions of equivalent strain rate in region Ⅲ with different back pressures and R values: (a) pb = 0 MPa; (b) pb = 100 MPa
图5(b)所示的R值的增加等效应变分布的趋势与文献[16]的结果一致:即随外角半径增大,材料挤压后的等效应变量随外转角半径增加而减小。WEI等[17]通过实验研究验证了不施加背压条件下,随着外转角半径减小,工件的等效应变分布均匀性变差。当R = 6 mm时,既消除了死区,同时也使等效应变量分布较为理想,这与VALIEV和LANGDON[18]的结果相吻合,说明模拟结果是可信的。在内转角Ф保持不变的情况下,适当的R值能协调工件上下表面的模具壁之间的相互作用力,平衡各部分因变形程度不同而引起的等效应变分布不均匀。同时,适当的R值能消除因死区而产生的粘滞带,当材料流经外转角时,不会产生因粘滞带导致的畸变区。因此,通过模拟分析可知,对于在450 ℃下挤压纯钛,本模拟选取R = 6、pb = 100 MPa是合理的。
3 结论
1) 当R = 0时,在外转角处因摩擦力作用产生的死区被材料填充,使工件Ⅲ区材料通过转角处时,材料之间相互搓动而产生剧烈变形,导致Ⅲ区等效应变激增,工件变形分布不均匀。
2) 当0<R<6 mm时,死区仍然存在,工件下表面与模具壁之间的相互作用力显著,仍有部分不均匀变形区存在;当R>6 mm时,工件上表面与模具壁相互作用力增加,Ⅰ区出现等效应变量大于Ⅲ区的现象,使工件变形不均;当R = 6 mm时,过渡区能有效协调工件表面的受力情况,得到比较均匀的等效应变分布。
3) 施加背压后,当R = 6时,工件的均匀变形区比不施加背压时提高10%左右,并且能使工件整体的等效应变量提高;但是背压并非越大越好,过大的背压导致Ⅰ区变形加剧,适当的配合R值与背压pb能得到均匀的等效应变量分布。对于纯钛,在450 ℃下进行ECAP变形时,选取R = 6 mm、pb = 100 MPa是合理的。
REFERENCES
[1] SEGAL V M, REZNIKOV V I, DROBYSHEVSKIY A E, KOPYLOV V I. Plastic working of metals by simple shear[J]. Russian Metall, 1981, 19(1): 99?105.
[2] VALIEV R Z, KRASILNIKOV N A, TSENEV N K. Plastic deformation of alloys with submicron-grained structure[J]. Mater Sci Eng A, 1991, 137: 35?40.
[3] VALIEV R Z, KORZNIKOV A V, MULYUKOV R R. Structure and properties of ultrafine-grained materials produced by severe plastic deformation[J]. Mater Sci Eng A, 1993, 168: 141?148.
[4] VALIEV R Z, ISAMGALIEV R K, ALEXANDROV I V. Bulk nanostructured materials from severe plastic deformation[J]. Prog Mater Sci, 2000, 45:103?189.
[5] NAGASEKHAR A V, YIP T H. Effect of acute tool-angles on equal channel angular extrusion/pressing [J]. Mater Sci Eng A, 2005, 410/411: 269?272.
[6] LI S, BOURKE M A M, BEYERLEIN I J, ALEXANDER D J, CLAUSEN B. Finite element analysis of the plastic deformation zone and working load in equal channel angular extrusion[J]. Mater Sci Eng A, 2004, 382: 217?236.
[7] OH S J, KANG S B. Analysis of the billet deformation during equal channel angular pressing[J]. Mater Sci Eng A, 2003, 343: 107?115.
[8] PARK J W, SUH J Y. Finite element analysis of material flow in equal channel angular pressing[J]. Scripta Mater, 2001, 44: 677?681.
[9] PRANGNELL P B, HARRIS C, ROBERTS S M. Finite element modelling of equal channel angular extrusion[J]. Scripta Mater, 1997, 37: 983?989.
[10] SHAN A, MOON I G, KO H S, PARK J W. Direct observation of shear deformation during equal channel angular pressing of pure aluminum[J]. Scripta Mater, 1999, 41: 353?357.
[11] WU Y, BAKER I. An experimental study of equal channel angular extrusion[J]. Scripta Mater, 1997, 37: 437?442.
[12] SUH J Y, KIM H S, PARK J W, CHANG J Y. Finite element analysis of material flow in equal channel angular pressing[J]. Scripta Mater, 2001, 44: 677?681.
[13] SON I H, LEE J H, IM Y T. Finite element investigation of equal channel angular extrusion with back pressure[J]. Mater Processing Technology, 2006, 171: 480?487.
[14] ZHERNAKOV V S, BUDILOV I N, RAAB D I, ALEXANDROV I V, VALIEV R Z. A numerical modelling and investigations of flow stress and grain refinement during equal-channel angular pressing[J]. Scripta Mater, 2001, 44: 1765?1769.
[15] CHUNG S W, SOMEKAWA H, KINOSHITA T, KIM W J, HIGASHI K. The non-uniform behavior during ECAE process by 3-D FVM simulation[J]. Scripta Mater, 2004, 50: 1079?1083.
[16] FURUNO K, AKAMATSU H, OH-ISHI K, FURUKAWA M, HORITA Z, LANGDON T G.. Microstructural development in equal-channel angular pressing using a 60° die[J]. Acta Mater, 2004, 52: 2497?2507.
[17] WEI Wei, WEI Kun-xia. Origin of inhomogenous behavior during equal channel angular pressing [J]. Scripta Mater, 2006, 54: 1865?1869
[18] VALIEV R Z, LANGDON T G.. Principles of equal-channel angular pressing as a processing tool for grain refinement[J]. Progress in Materials Science, 2006, 51: 881?891.
基金项目:国家安全重大基础研究资助项目
收稿日期:2008-05-16;修订日期:2008-09-17
通讯作者:丁 桦,教授;电话:024-83687746;E-mail: hding@263.net
(编辑 龙怀中)