Trans. Nonferrous Met. Soc. China 31(2021) 53-73

Microstructural evolution, flow stress and constitutive modeling of Al-1.88Mg-0.18Sc-0.084Er alloy during hot compression

Fu-rong CAO^1,2,3, Bin YIN⁴, Si-yuan LIU¹, Lu SHI¹, Shun-cheng WANG⁵, Jing-lin WEN¹

1. School of Materials Science and Engineering, Northeastern University, Shenyang 110819, China;

2. Key Laboratory of Lightweight Structural Materials of Liaoning Province, Northeastern University, Shenyang 110819, China;

3. State Key Laboratory of Rolling and Automation, Northeastern University, Shenyang 110819, China;

4. Wuhu Cowin Automobile Co., Ltd., Wuhu 241000, China;

5. Institute of Materials Processing and Forming Technology, Guangdong General Research Institute of Industrial Technology, Guangzhou 510650, China

Received 7 April 2020; accepted 7 September 2020

Abstract: To explore the hot compression behavior and microstructural evolution, fine-grained Al-1.88Mg-0.18Sc- 0.084Er (wt.%) aluminum alloy wires were fabricated with Castex (continuous casting-extrusion) and ECAP-Conform, and their hot compression behavior was investigated at temperatures of 673-793 K and strain rates of 0.001-10 s^-1; the microstructures were characterized by optical microscope, X-ray diffractometer, transmission electron microscope, and electron backscattered diffractometer, and the flow stresses were obtained by thermal compression simulator. Microstructural evolution and flow curves reveal that dynamic recovery is the dominant softening mechanism. Continuous dynamic recrystallization followed by dynamic grain growth takes place at a temperature of 773 K and a strain rate of 0.001 s^-1; the yielding drop phenomenon was discovered. Hyperbolic sine constitutive equation incorporating dislocation variables was presented, and a power law constitutive equation was established. The stress exponent is 3.262, and the activation energy for deformation is 154.465 kJ/mol, indicating that dislocation viscous glide is the dominant deformation mechanism.

Key words: Al-Mg alloy; ECAP-Conform; hot compression; microstructure; flow stress; constitutive equation

1 Introduction

Due to significant grain refinement and resulting excellent mechanical properties, severe plastic deformation (SPD) has attracted much attention from the extensive researchers during past decades. Except for the conventional deformation methods such as rolling [1] and extrusion [2],  available SPD approaches include high-pressure torsion (HPT) [3], equal channel angular pressing (ECAP) [4], multi-directional forging (MDF) [5], accumulative roll bonding (ARB) [6], friction stir processing (FSP) [7], cryomilling [8] and so on. ECAP-Conform in which Conform means continuous extrusion forming is one of the SPD methods, which is a further development of ECAP and can achieve continuous ECAP [9-11]. Alloy wire can be extruded out of the die continuously as long as the feedstock is fed into the entrance of the machine wheel. Castex (continuous casting- extrusion) is a further development of Conform, and liquid metal in Castex is used to replace solid feedstock in Conform [12-14]. However, little work is available about the combination of Castex and ECAP-Conform. Therefore, an approach to produce high performance Al-Mg alloy wires is proposed by combining Castex and ECAP- Conform.

Al-Mg alloys are non-heat-treatable strengthening alloys and have been widely used in automobile and aerospace industries because of their moderate strength and excellent resistance to corrosion [15]. Recently, Al-Mg alloys have been moderately investigated. PENG et al [16] investigated the hot compression behavior of rolled and homogenized Al-3.2Mg-0.4Er aluminum alloy using processing map. MALOPHEYEV et al [17] studied the friction stir welding (FSW) of Al-5.4Mg-0.2Sc-0.1Zr alloy processed by ECAP and hot (or cold) rolling. CAO et al [18] investigated the superplasticity in a rolled Al-6.1Mg-0.25Sc-0.3Mn-0.1Zr alloy. WANG et al [19] investigated the dimensionless parameter in the constitutive equation of superplasticity in an Al-5.33Mg-0.23Sc-0.49Mn alloy. KIM et al [20] investigated the dynamic restoration mechanism of Al-5Mg-(0-0.1) Ca alloy during hot compression. DAI et al [21] studied the hot deformation behavior and the constitutive equation of Al5083 (Al-4.8Mg-0.5Mn) alloy. CHEN et al [22] investigated the hot deformation behavior and constitutive equation of Al-9Mg-1.1Li-0.5Mn alloy. According to our literature analysis, these alloys belong to the Al-Mg alloys of Er, Sc, Ca, Mn, and Li addition which rely on Al₃Er, Al₃Sc, Al₄Ca, Al₆Mn, and Al₃Li compounds to strengthen the Al matrix. Also, these research reports are related to the high-temperature deformation behavior of Er, Sc, Ca, Mn, and Li added Al-Mg alloys such as hot compression, hot FSW, and hot tensile deformation. To the best of our knowledge, no work is available studying on the alloying and the high-temperature deformation behavior of an Al-Mg-Sc-Er alloy. Therefore, firstly, we designed a novel Al-2Mg- 0.2Sc-0.2Er (wt.%) alloy. Secondly, to provide basic data for calculation of deformation force, hot compression tests are required to obtain the flow stress curves and to investigate the microstructural evolution. Although most of the reports on hot compression of aluminum alloys were associated with the Al-Zn-Mg, Al-Mg-Si, and Al-Cu alloys [23-28], and only aforementioned limited reports of hot compression behavior were reported in Al-Mg alloys, the hot compression study of Al-Mg-Sc-Er alloy remains unknown. In view of these, it is necessary to investigate the microstructure in an Al-2Mg-0.2Sc-0.2Er alloy wire processed by Castex and ECAP-Conform and to study its hot compression behavior and microstructural evolution. Besides investigation of these aspects, dynamic softening mechanisms and constitutive modeling during hot compression should be considered next.

The dynamic softening mechanisms and constitutive equations during the hot compression are a focused topic. The dynamic softening  mechanisms include the dynamic recovery, discontinuous dynamic recrystallization, continuous dynamic recrystallization, and geometrical dynamic recrystallization [29]. Dynamic recrystallization of aluminum alloys is still controversy. Dynamic softening mechanism in Al-Mg-Sc-Er alloy is unknown. Therefore, it is necessary to investigate the flow stress and microstructural evolution and to elucidate the dynamic softening mechanisms in this alloy. Constitutive equations can be classified into three categories: physical-based models, phenomenological models, and artificial neuron network models [30]. Arrhenius type equation is one of the phenomenological constitutive equations and has attracted extensive attention owing to its high accuracy of prediction of flow stress [31,32]. However, since phenomenological Arrhenius equation is lack of specific physical meaning, it is difficult to explain the physical phenomenon such as microstructural characteristics during hot compression. According to our literature survey, little information is available to link dislocation variables to the Arrhenius equation. The Arrhenius constitutive equation containing dislocation variables can be applied in Castex and ECAP-Conform processes and has both scientific value and practical significance. Thus, it is necessary to establish a constitutive relationship between dislocation variables and flow stress. On the other hand, power law constitutive equations have been often used in tensile superplasticity and creep research and are especially suitable for elucidation of deformation mechanism at elevated temperatures [33]. Little information is available on establishing a power law constitutive equation in this alloy during hot compression. Hence, it is necessary to establish the power law equation in the Al-Mg-Sc-Er alloy during hot compression.

In this work, Al-2Mg-0.2Sc-0.2Er alloy wires with 8 mm in diameter were fabricated by Castex and ECAP-Conform. The microstructural evolution during Castex and ECAP-Conform was investigated. The mechanical properties and microstructures during hot compression were studied. An Arrhenius equation considering dislocation variables and a power law constitutive equation were established. It is expected that the first report on hot compression behavior of Al-Mg-Sc-Er alloy processed by Castex and ECAP-Conform stimulates the interests of researchers in relevant research fields.

2 Experimental

2.1 Material preparation

Commercially pure aluminum, pure magnesium, Al-20wt.%Sc and Al-20wt.%Er master alloys were chosen as the raw materials. Commercially pure aluminum was melted at 1023 K in an intermediate frequency induction furnace. Then, the master alloys and pure magnesium were put into the furnace and melted. The melt was degassed by carbon hexachloride at 1023 K, and stirred to obtain uniform mixing. The slag on the melt surface was removed to avoid the formation of porosity or void during the following Castex. Detailed process of Castex is shown in Fig. 1(a) or was shown elsewhere [34]. The melt was poured at 993 K into the entrance of Castex machine through the tundish, solidified at a solidification rate of 390 K/s, and deformed along the groove of Castex wheel with circulated cooling water in the interior. Then, the solid alloy was forced to turn 90° at the abutment, deformed in the mini-container, and extruded out of the extrusion die to obtain wires with 8 mm in diameter. The analyzed chemical composition of Castex wire was 1.88 wt.% Mg, 0.18 wt.% Sc, 0.084 wt.% Er, and balanced Al. The schematic diagram of ECAP- Conform process is shown in Fig. 1(b). Solid wires made by Castex were fed into the Conform wheel, deformed at 298 K along the groove of Conform wheel at a velocity of 146.5 mm/s, forced to turn 90° at the abutment and deformed, and extruded out of the die. Here, near L-type channel had the function of ECAP. This process was repeated four times. This means that four-pass ECAP-Conform was completed.

2.2 Hot compression tests

Cylindrical samples of d8 mm × 15 mm were prepared from the ECAP-Conform wire. Hot compression tests were made on an MMS300 thermal simulation testing machine. The testing temperatures were 673, 723, 773, and 793 K. The strain rates were 0.001, 0.01, 0.1, 1, and 10 s^-1. The compression strain was 0.6. During hot compression, the samples were firstly heated to the designated temperatures at a heating rate of 278 K/s and held for 3 min. After the tests, the compressed samples were water-quenched to room temperature to reserve the high-temperature microstructures.

2.3 Microstructural examinations

The specimens for optical microscopy (OM) examination were mechanically ground and polished. Then, electrolytic polishing was conducted in a solution of 70 vol.% perchloric acid + 9 vol.% alcohol followed by anode coating in a solution of 38 vol.% concentrated sulfuric acid + 43 vol.% phosphoric acid + 19 vol.% water. The prepared specimens were observed on an Olympus DSX500 optical microscope. Image Pro-Plus (IPP) software was used to measure the grain size.

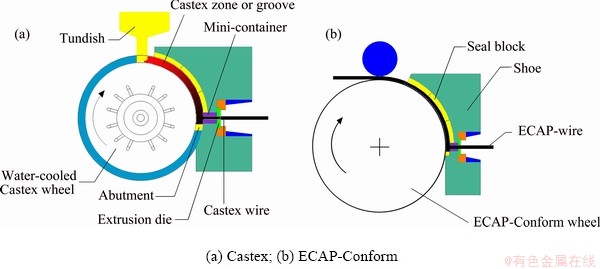
Fig. 1 Schematic diagrams of alloy manufacturing

The specimens for X-ray diffraction (XRD) examination were mechanically ground and polished. The polished specimens were examined on an X'Pert Pro diffractometer. Phase compositions were analyzed by an X’Pert HighScore Plus software.

The specimens for transmission electron microscopy (TEM) examination were thinned down to 50 μm. Then, the specimens were twin-jetted in an electrolyte of 30 vol.% nitric acid + 70 vol.% alcohol. The prepared discs were observed on a Tecnai G20 transmission electron microscope. In the meantime, energy dispersive spectroscopy  (EDS) analyses were performed.

The specimens for electronic backscattered diffraction (EBSD) characterization were prepared as follows: the specimens was ground by abrasive papers, mechanically polished, and further polished by ion beam polishing on a LEICA EM RES101 ion beam polisher. EBSD analysis was carried out on an LEO Super35 field emission SEM furnished with an Oxford EBSD analysis system.

3 Results

3.1 Initial microstructures and phase composition of alloy after Castex and ECAP-Conform

Figure 2 shows the optical microstructures and grain sizes of Al-1.88Mg-0.18Sc-0.084Er alloy processed by Castex and ECAP-Conform. As shown in Figs. 2(a) and (b), grains on the cross- section and longitudinal section of as-Castex state are equiaxed and distributed homogeneously with grain sizes of (53.56±4.30) and (63.40±3.60) μm, respectively. The average grain size of Castex wire is (58.48±3.95) μm. The grains are refined as compared with conventional cast aluminum alloys. As shown by the longitudinal section in Figs. 2(c) and (d), the grain sizes in the core and the edge of the 4th pass of ECAP-Conform are refined to (4.96±1.30) and (4.08±0.90) μm, respectively, and average grain size is (4.52±1.10) μm. The grains are distributed homogeneously, but elongated grains are visible. This result indicates that pronounced refinement occurs during the ECAP-Conform process.

Fig. 2 OM images and average grain sizes at different sampling positions of Al-1.88Mg-0.18Sc-0.084Er alloy processed by Castex and ECAP-Conform

Figure 3 shows the XRD pattern of Al- 1.88Mg-0.18Sc-0.084Er alloy in as-Castex state. Analysis of phase composition reveals that this alloy consists of α(Al) solid solution phase, Mg₂Al₃, Al₁₂Mg₁₇, Al₂Sc, and Al₃Er intermetallic compounds. Particular discovery of Al and Sc compound is the existence of Al₂Sc compound instead of Al₃Sc compound that is a coherent L1 structured compound. The α(Al) solid solution phase achieves the solid solution strengthening while the intermetallic compounds achieve the second phase strengthening.

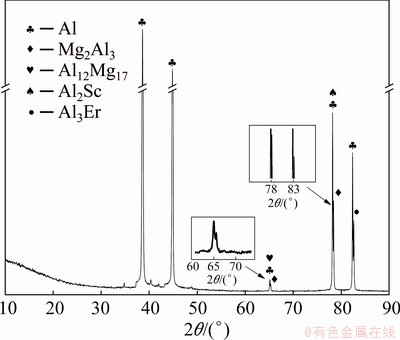
Fig. 3 XRD pattern of Al-1.88Mg-0.18Sc-0.084Er alloy in as-Castex state

3.2 True stress-true strain curves during hot compression

Figure 4 shows the true stress-true strain curves during hot compression at different temperatures with different strain rates. The deformation temperatures and strain rates have a significant influence on the flow stress level. The flow stress level decreases with increasing the temperature and/or decreasing the strain rate. That is because the increase in temperature accelerates atomic diffusion and thermal activation process, lowers the dislocation density, and leads to the hot softening of the alloy; the decrease in the strain rate increases the time of atomic diffusion and thermal activation, lowers the dislocation density, and results in the hot softening of the alloy. As a result, the flow stress decreases.

As shown in the flow curves, the true stress increases with the increase in the strain until the peak stress. In this case, dislocation multiplication is enhanced and work-hardening appears. After the peak stress, the flow stress curves exhibit different characteristics. As shown in Fig. 4(a), at a strain rate of 0.001 s^-1, flow stress increases with the increase in the strain and exhibits obvious work-hardening at various temperatures. This may be related to the dynamic grain growth. As shown in Figs. 4(b)-(d), most of flow curves exhibit horizontal plateau, which indicates the occurrence of the dynamic recovery (DRV). In this case, dislocation rearrangement and annihilation achieve a balance. The DRV behavior in this alloy is quite similar to Al-Zn-Mg-Er-Zr alloys [35,36]. However, exceptional cases occur. At strain rates of 0.1 s^-1 (673 K) and 1 s^-1 (723 K), respectively, the flow stress exhibits work-softening (Fig. 4(c) and (d)), which indicates the occurrence of dynamic recrystallization (DRX). At a strain rate of 1 s^-1 (673 K), the flow stress exhibits work-hardening (Fig. 4(d)). This work-hardening behavior is different from the work-softening behavior at strain rates of 0.01 and 0.1 s^-1 (Figs. 4(b) and (c)). The former work-hardening indicates that high strain rate does not ensure enough time to soften the sample, and hardening exceeds softening. However, the latter work-softening indicates that lower strain rates ensure enough time to soften the samples, and softening exceeds hardening. This phenomenon is a result of competition between hardening and softening. At strain rates of 0.01 and 1 s^-1 and 793 K, the flow curves exhibit work-hardening in later stage (Figs. 4(b) and (d)). As shown in Fig. 4(e), the flow stress exhibits multi-peak oscillations at a strain rate of 10 s^-1, but in terms of the changing trend, DRV instead of DRX dominates. This oscillating phenomenon can be explained by the flow instability such as flow localization of the compressed specimen when the strain rate is too high [37]. Meanwhile, since stress undulation during DRX is usually accompanied by the decrease in flow stress with the increase of strain during deformation [38], the possibility of DRX at a strain rate of 10 s^-1 is ruled out in the present alloy. Except for this strain rate of 10 s^-1, oscillating phenomenon also occurs at other strain rates  shown in Figs. 4(a)-(d) probably because periodic oscillation is caused by the pinning and depinning of solute atmosphere. Long periodic strain hardening occurs at 0.001 s^-1 in Fig. 4(a) due to dynamic grain growth. The oscillation shaped stress-strain curves in Figs. 4(b)-(d) are caused by short strain hardening starting after the end of strain softening. This strain softening is reflected in the lower yield point while the short strain hardening is reflected in the flow stress curve after the lower yield point. This V-shaped softening is different from the strain softening created by DRX or DRV which can be justified by the analysis of flow stress curve and microstructural examination. Usually, DRX or DRV researchers believe that persistence of long horizontal flow stress plateau with increasing strain after yield stress indicates the occurrence of DRV, but DRX occurs after the peak stress followed by the decrease in flow stress with increasing strain.

Fig. 4 True stress-true strain curves of Al-1.88Mg-0.18Sc-0.084Er alloy hot-compressed at different temperatures with different strain rates and strain of 0.6

Yielding drop phenomenon appears in Figs. 4(b)-(e). Dislocations are immobilized to lead to the increase in applied stress (upper yield point) due to pinned Cottrell’s solute atmosphere, and dislocations are mobilized to lead to the decrease in the applied stress (lower yield point) due to depinned Cottrell’s solute atmosphere. That is the cause of yielding drop. It is found that with  the increase in strain rate and/or decrease in temperature, the degree of yielding drop increases. The analysis of this phenomenon can be accurately predicted by the models for Al-(5-13)wt.%Mg alloy in Ref. [39]. However, as shown in Fig. 4(e), at a temperature of 673 K and a strain rate of 10 s^-1, the yielding drop is contrary to former prediction and needs to be studied in future.

During the deformation of the present alloy, there exists deformation heat effect. The instantaneous true temperature (T) is equal to the preset temperature (T_pre) plus the temperature rise (△T) [40]. The temperature rise abides by the following relation [4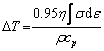1]:

                         (1)

where η is the adiabatic correction factor, σ is the true stress, ε is the true strain, r is the density, c_p is the specific heat capacity, and rc_p is the heat capacity. For our purpose of calculating the deformation force using principal stress method, peak stress is usually chosen and peak stress correction is necessary, but finite element simulation needs corrections at different strains. Moreover, according to our literature survey, the flow stress is seldom corrected in the range of 0.001-1 s^-1, but the flow stress must be corrected at a high strain rate of 10 s^-1. As a result, Fig. 4(e) shows the points of corrected peak stress.

3.3 Microstructural evolution of alloy during hot compression

3.3.1 Effect of deformation temperature on micro- structural evolution

Fig. 5 OM images and grain sizes of Al-1.88Mg-0.18Sc-0.084Er alloy hot-compressed at different temperatures with strain rate of 0.01 s^-1 and strain of 0.6

Figure 5 shows the optical micrographs and grain sizes of the present alloy hot-compressed at different temperatures with a strain rate of 0.01 s^-1 and a strain of 0.6. The grain sizes range from (3.6±0.60) to (7.80±1.20) μm and increase with increasing the deformation temperature. This result indicates that grain growth gradually occurs with the increase in the deformation temperature because high temperature accelerates atomic diffusion, promotes boundary migration, and leads to dynamic grain growth. As shown in Figs. 5(a)-(c), the microstructures are basically equiaxed grains, and the grain sizes are in the range of (3.6±0.60) to (5.20±0.90) μm, corresponding to the grain sizes of (4.96±1.30) and (4.08±0.90) μm in the 4th-pass of ECAP-Conform alloys. The variation in grain size is not large. In consideration of the flow stress curves in Fig. 4(b), microstructural evolution is consistent with the DRV curves. As shown in Fig. 5(d), grain elongation is visible, and grain size reaches (7.80±1.20) μm. This means that grain growth occurs, which is in good agreement with the slight strain-hardening in later stage of the flow stress curve at 793 K and 0.01 s^-1 in Fig. 4(b). Moreover, grain distribution is not homogeneous, and elongated grains coexist with fine grains.

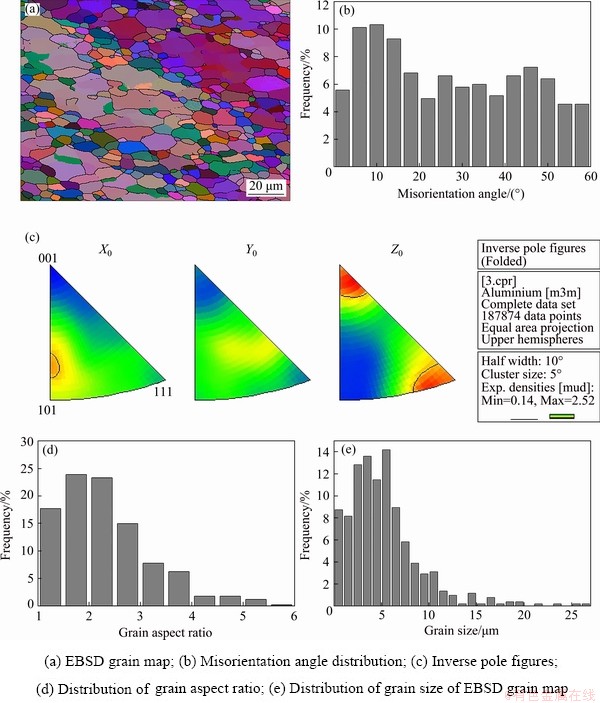
Fig. 6 EBSD analysis results of Al-1.88Mg-0.18Sc-0.084Er alloy hot-compressed at 793 K with strain rate of 0.01 s^-1 and strain of 0.6

Figure 6 shows the EBSD analysis results of the present alloy hot-compressed at a temperature of 793 K with a strain rate of 0.01 s^-1 and a strain of 0.6 after the alloy of Fig. 5(d) is examined by EBSD. As shown in Fig. 6(a), the microstructure consists of large and elongated grains surrounded by small and fine grains. Large and elongated grains are non-DRX grains, whereas small and fine grains are full-DRX grains. This indicates that incomplete DRX occurs under this condition. As shown in Fig. 6(b), low-angle grain boundaries (misorientation angle <15°) and high-angle grain boundaries (misorientation angle ≥15°) coexist, which further confirms the existence of incomplete DRX. As shown in Fig. 6(c), inverse pole figures show that strong <011> and <111> textures exist, which is consistent with the grain morphology in Fig. 6(a). Grain aspect ratio (GAR) is defined as the ratio of longitudinal grain size to transverse grain size. During superplasticity, GAR of equaixed grains is usually in the range of 1-1.2, and occasionally has been reported to be 1.5 recently in shear punch superplasticity. Thus, during this compression process, grains with GARs in the range of 1-1.5 are deemed as equiaxed grains; whereas grains with GARs more than 1.5 are deemed as elongated grains. As shown in Fig. 6(d), GAR ranges from 1.0 to 6.0 and reflects the coexistence of equiaxed grains and elongated grains. As shown in Fig. 6(e), the average grain size determined by EBSD is 5.2 μm and is less than (7.80±1.20) μm determined by the optical microscope. This deviation in grain size is because the optical microscope is difficult to identify rather small grains. Therefore, it seems reasonable to suggest the microstructural evolution under this condition as the incomplete DRX followed by dynamic grain growth. Strain hardening rate or softening rate means the slope of true stress-true strain curve. According to Fig. 4(b), the strain hardening rate slightly exceeds the incomplete DRX softening rate. As a result, strain hardening slightly predominates. The grain growth phenomenon in Fig. 6(e) is consistent with the slight strain hardening at 793 K and 0.01 s^-1 in Fig. 4(b).

3.3.2 Effect of strain rate on microstructural evolution

Figure 7 shows the optical micrographs and grain sizes of present alloy hot-compressed at a temperature of 773 K with different strain rates and a strain of 0.6. The grain size decreases with increasing the strain rate. As shown in Fig. 7(a), at a lower strain rate of 0.001 s^-1, the grain size is (8.70±1.40) μm and indicates the occurrence of dynamic grain growth. Dynamic grain growth leads to higher resistance to deformation at elevated temperatures and results in strain hardening. This microstructure is consistent with the flow stress curve of strain hardening at 773 K in Fig. 4(a). As shown in Figs. 7(b)-(e), grain sizes are in the range from (4.36±0.50) to (5.30±1.20) μm. Compared with the grain sizes of (4.96±1.30) and (4.08±0.90) μm after the 4th-pass of ECAP- Conform, the grain sizes vary little, which indicates that DRV dominates under these conditions. This result is consistent with the flow stress curves of DRV at 773 K in Figs. 4(b)-(e).

Figure 8 shows the EBSD analysis results of the present alloy hot-compressed at a temperature of 773 K with a strain rate of 0.001 s^-1 and a strain of 0.6. Grains take on equiaxed shape (Fig. 8(a)). The fraction of high-angle grain boundaries accounts for more than 90% (Fig. 8(b)). <011> crystal direction reflects the trace of weak elongated grains, and textures are basically randomized (Fig. 8(c)). GARs of most grains are within the range of 1.0-1.8 (Fig. 8(d)). All the evidences confirm the occurrence of full or complete DRX. The average grain size determined by EBSD is 5.6 μm and is less than (8.70±1.40) μm determined by optical microscope. The cause of this deviation in grain size is similar to that in Section 3.3.1. Dynamic grain growth takes place. Therefore, it seems reasonable to suggest the microstructural evolution under this condition as the complete DRX followed by dynamic grain growth. Strain hardening rate or softening rate means the slope of true stress-true strain curve. According to Fig. 4(a), the strain hardening rate surpasses the DRX softening rate. As a result, strain hardening predominates. The dynamic grain growth phenomenon in Fig. 8(e) is consistent with the strain hardening at 773 K and 0.001 s^-1 in Fig. 4(a).

Fig. 7 OM images and grain sizes of Al-1.88Mg-0.18Sc-0.084Er alloy hot-compressed at 773 K with different strain rates and strain of 0.6

Figure 9 shows the TEM images of the present alloy hot compressed at a temperature of 773 K and a strain rate of 0.001 s^-1. Particles or intermetallic compounds are clearly seen. Interaction between dislocations and particles is visible. The particle size is no more than 0.5 μm. The results of EDS analyses are shown in Table 1. In Al-1.88Mg- 0.18Sc-0.084Er alloy, Mg compound cannot be found through EDS, and this indicates that Mg element is mainly solutionized in the aluminum matrix. Compared to the XRD results in Fig. 3, the phase composition of these particles may be AlFe_xEr_y (Points A and B), Al₃Fe₄ (Point C), and AlSc_zEr_y (Points D, E, and F). Although Er content is only 0.008%, its compounds are still discovered under TEM.

If the particle size is less than 1 μm, the particle stimulated nucleation (PSN), a kind of discontinuous dynamic recrystallization (DDRX), is prohibited [42]. Since the particle size in Fig. 9 is less than 1 μm, the possibility of PSN or DDRX is ruled out. In the meantime, since aluminum has high stacking fault energy (SFE), high SFE is favorable for the occurrence of DRV rather than DDRX. The present alloy only contains 1.88 wt.% Mg, and its SFE will be higher. Thus, the possibility of DDRX is ruled out in the present alloy.  According to aforementioned microscopic analyses in Figs. 7 and 8 and corresponding flow stress curve in Fig. 4(a), DRV is ruled out, and continuous DRX (CDRX) followed by dynamic grain growth takes place under this condition. It is generally recognized that high temperature and low strain rate accelerate DRX, and CDRX involves the transformation of low-angle grain boundaries into high-angle grain boundaries [43,44]. Moreover, the existence of dislocations inside a grain demonstrates the occurrence of CDRX [45]. These evidences further support our conclusion that CDRX followed by dynamic grain growth takes place at a high temperature of 773 K and a lower strain rate of 0.001 s^-1.

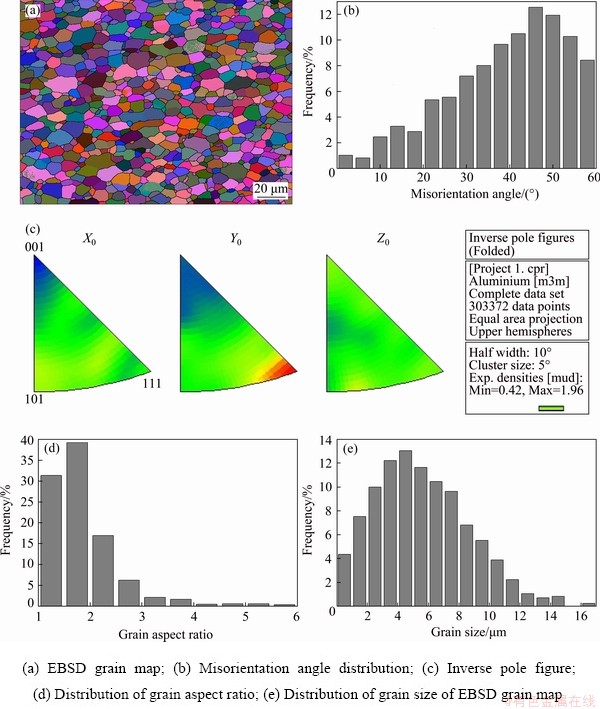
Fig. 8 EBSD analysis results of Al-1.88Mg-0.18Sc-0.084Er alloy hot-compressed at 773 K with strain rate of 0.001 s^-1 and strain of 0.6

3.4 Establishment of constitutive equations during hot compression

3.4.1 Hyperbolic sine constitutive equation incorporating dislocation variables

Arrhenius constitutive equations that reflect the dependence of flow stress on temperature and strain rate at a certain strain are given by [46-48]

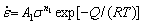 (ασ<0.8)           (2)

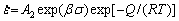 (ασ<1.2)       (3)

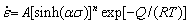 (for all σ)     (4)

where is the strain rate, A₁, A₂ and A are material constants, α is the material constant, σ is the flow stress, here, peak stress is chosen in Fig. 4, n is the stress exponent, n₁ and β are material constants, Q is the activation energy for deformation, R is the mole gas constant (8.314 J/(mol·K)), and T is the absolute deformation temperature. Equation (4) is a hyperbolic sine equation.

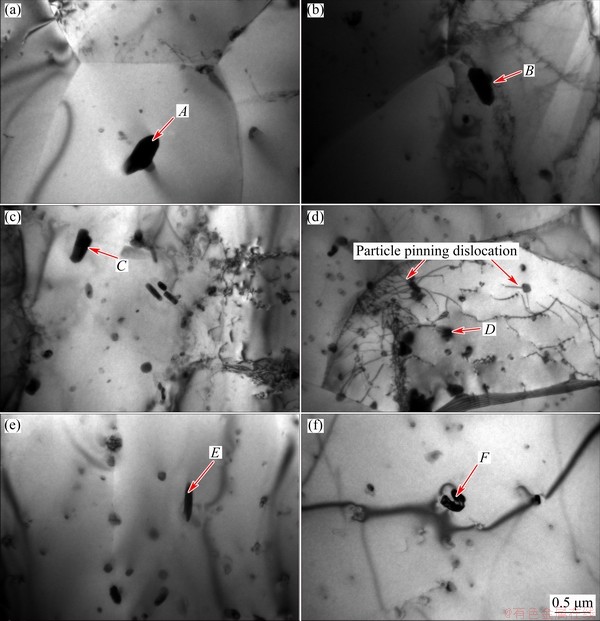
Fig. 9 TEM images of Al-1.88Mg-0.18Sc-0.084Er alloy hot-compressed at 773 K and strain rate of 0.001 s^-1 (Points A, B, C, D, E, and F indicate second phase particles)

Table 1 EDS analysis results of Al-1.88Mg-0.18Sc-0.084Er alloy

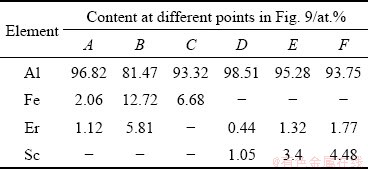
Figure 10 shows the evaluation curves to obtain the material constants. According to the mean slopes of the curves in Figs. 10(a) and (b), n₁=4.629 and β=0.130 MPa^-1, respectively. Hence, α=β/n₁=0.0281 MPa^-1. According to the mean  slope of the curve in Fig. 10(c), n=3.262. Based on Fig. 10(d), the average activation energy for deformation, Q, was calculated to be 154.465 kJ/mol, which is higher than the theoretical activation energy for lattice diffusion of aluminum, 143.4 kJ/mol [49]. This is because the second phase particles in this alloy obstruct the movement of dislocations, raise the resistance to deformation, and increase the activation energy. The stress exponent is 3.262, and the activation energy for deformation is 154.465 kJ/mol, indicating that dislocation viscous glide is the dominant deformation mechanism.

Equation (4) is rewritten by introduction of Z (Zener-Hollomon) parameter as follows [50]:

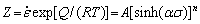        (5)

The following logarithmic relation can be obtained by Eq. (5):

ln Z=ln A+nln[sinh(ασ)]                   (6)

The relation curve of ln Z-ln[sinh(ασ)] was plotted to obtain A value, as shown in Fig. 11(a). n=3.24 as per the slope of this curve, and ln A=21.55 as per the intercept of this curve. Thus, the hyperbolic sine constitutive equation is obtained according to Eq. (4):

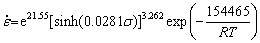   (7)

The correlation coefficient, 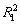, is 0.9552.

Fig. 10 Evaluation curves of ln-lns (a), ln-s (b), ln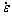-ln[sinh(ασ)] (c) and ln[sinh(αs)]-1/T (d)

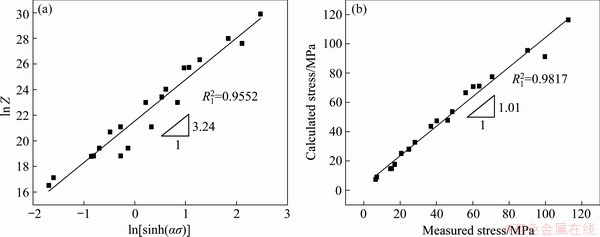
Fig. 11 Relation curves of ln Z-ln[sinh(αs)] (a) and comparison of calculated stress with experimental one (b)

Flow stress can be expressed by the Z parameter by mathematical treatment:

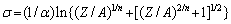
Thus, the following constitutive equation can be obtained:

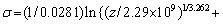
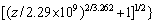=F(Z)        (8)

Figure 11(b) shows the results comparison between the calculated stress and the measured stress. Good agreement is achieved with a correlation coefficient of 0.9817 and an average absolute relative error of only 1%.

In our previous work, we established the constitutive relationship of dislocation density and number of dislocations with Z parameter during hot tensile deformation [51]. However, calculation is not made there. Here, we extended this relationship during hot tensile deformation to the hot compression process. Thus, the parameter Z-related constitutive equations containing the dislocation density and number of dislocations during hot compression can be given by

ρ=C(Gb)^-2[F(Z)]²                         (9)

N=1.81(1-v)[d/(Gb)]F(Z)                 (10)

where ρ is the dislocation density, C is a dimensionless constant, G is the shear modulus, and b is the magnitude of Burgers vector, F(Z) (Eq. (8)), N is the mean number of dislocations inside the grain, v is Poisson ratio, and d is the average linear intercept grain size.

Equations (9) and (10) reflect the constitutive relationship between the dislocation density and parameter Z, and the constitutive relationship between the mean number of dislocations inside the grain and parameter Z, respectively, during hot compression.

Now, calculation was made for a hot compression condition: T=773 K, =0.001 s^-1, F(Z)=9.086 MPa (Eq. (8)), d=8.70 μm (Fig. 7 (a)), C=10 [52], v=0.34 [53], and b=0.286 nm [53].

G is given by [54]

G=E/[2(1+v)]                          (11)

where E is the elastic modulus.

E of aluminum is given by [55]

E=77630-12.98T-0.03084T²                    (12)

Substituting of T=773 K and v=0.34 into Eqs. (11) and (12), we obtained G=18350.98 MPa. Substituting aforementioned data into Eqs. (9) and (10), we obtained ρ=2.99×10¹³ m^-2 and N=18 during hot compression at 773 K and 0.001 s^-1. On one hand, the experimental dislocation density can be obtained by XRD line broadening approach. Integral breadth analysis was used to calculate coherent diffraction domain size (d') and lattice strain (2>^1/2) by the following equation [56]:

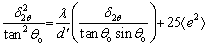          (13)

where △_2θ is the measured integral breadth and equals 0.9 times the full-width at half maximum (FWHM) height of the diffraction peaks [57], θ_o is the peak maximum position, λ is the wavelength of Cu K_α radiation (λ=0.15405 nm) [58], and e is the lattice strain.

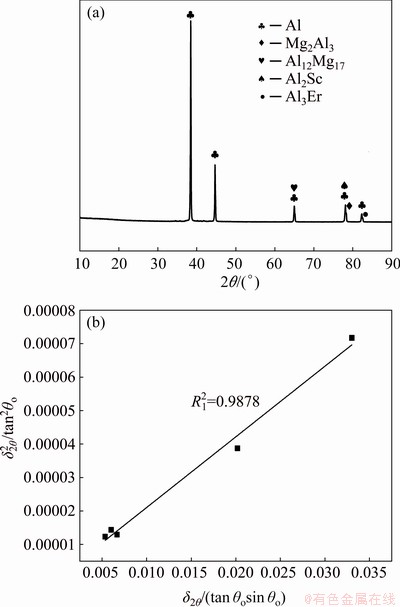
Fig. 12 XRD pattern for the 4th-pass ECAP-Conform specimen (a) and integral breadth analysis to calculate coherent scattering domain size and lattice strain from XRD data (b)

Figure 12(a) shows the XRD pattern of the specimen. Figure 12(b) presents the least square fit of 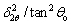 against △_2θ/(tan θ_osin θ_o) for all measured peaks. The correlation coefficient is 0.9878. According to Eq. (13), we obtained d′=73 nm and 2>=4.88×10^-9.

Dislocation density, ρ, is given by [59]

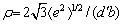                     (14)

Substituting aforementioned d′ and 2> data into Eq. (14), we obtained ρ=1.16×10¹³ m^-2. The experimental dislocation density, 1.16×10¹³ m^-2, is close to the estimated dislocation density, 2.99×10¹³ m^-2. Moreover, it was reported that the dislocation density of AA1050 aluminum alloy annealed at 643 K is 7.0×10¹² m^-2 [60], and the dislocation density of cold rolled Al-Mg-Cu-Mn alloy is 2.2×10¹⁴ m^-2 [61]. The dislocation density of the present alloy hot-compressed at 773 K and 0.001 s^-1 lies between both data. These evidences indirectly demonstrate the rationality of our data. On the other hand, the experimental number of dislocations, 21, in Fig. 9(d) is approximately consistent with the estimated number of dislocations, 18. We used random sample to make random TEM experiment and count the number of dislocations, and used the newly established constitutive model to calculate the number of dislocations. They are all randomized. Thus, this consistency is convincing.

3.4.2 Power law type constitutive equation

The power law constitutive equation for high temperature deformation is generally expressed as follows [62]:

     (15)

where  is the steady-state deformation rate, A′ is a dimensionless constant, p is the grain size exponent, σ is the applied stress, σ₀ is the threshold stress, n is the stress exponent, D₀ is the frequency factor for diffusion, Q is the activation energy for deformation, and k is the Boltzmann constant.

Determination of the threshold stress σ₀ and true stress exponent n: Here, true stress was chosen at a true strain of 0.2 in Fig. 4. Figure 13 shows the relation curves of σ-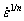 (n=2, 3, 4, and 5) that were plotted to obtain the best linear fitting. The intercept of the fitted line on the stress axle at zero strain rate is the threshold stress. The correlation coefficients for σ- 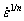(n=2, 3, 4, and 5) were 0.8899, 0.9407, 0.9638, and 0.9750, respectively. However, since negative threshold stress for n=5 appears, n=5 is unreasonable. Thus, the best fitting true stress exponent n=4 with a correlation coefficient of 0.9638.

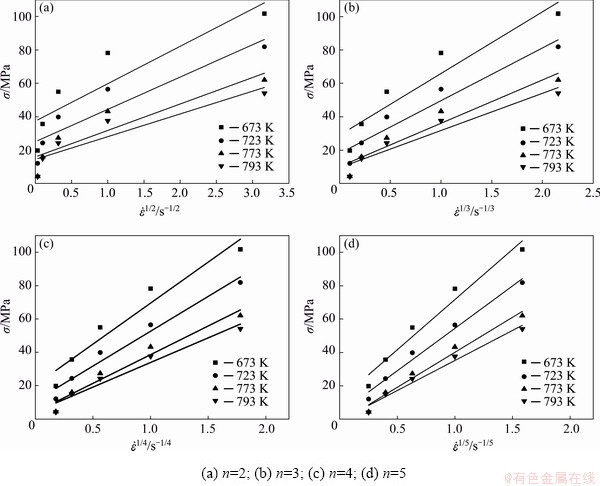
Fig. 13 Curves of true stress σ against 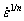 for alloy

Determination of activation energy for deformation: True activation energy for the deformation can be obtained as per Eq. (15).

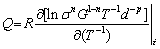                (16)

The estimated true stress exponent (n value) indicates a dislocation creep mechanism, p=0 [63]. Figure 14(a) shows the curves of experimental activation energy. The values of experimental activation energy are in the range of 72.5-172.3 kJ/mol. The theoretical activation energy for grain boundary diffusion is 84 kJ/mol while the theoretical activation energy for lattice diffusion is 143.4 kJ/mol [49]. The experimental activation energy of 72.5-172.3 kJ/mol indicates that atomic diffusion mechanism experiences a transition from grain boundary diffusion at higher strain rate to lattice diffusion at lower strain rate. Abnormal high activation energy of 172.3 kJ/mol at a strain rate of 0.001 s^-1 may be attributed to dynamic grain growth and increase in the resistance to deformation due to the existence of intermetallic compounds.

Fig. 14 Relationships between ln(σⁿG^1-nT ^-1) and T  ^-1 (a), and between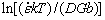and ln[(σ-σ₀)/G] (b)

Equation (15) is simplified as follows at p=0 and D₀=10^-4 m²/s[64]:

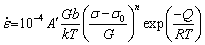          (17)

Figure 14(b) presents the normalized curve of 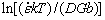 against ln[(σ-σ₀)/G] in order to get n value and A′ value in Eq. (17). The slope of normal regression curve is 3.36. Thus, n=3.36. Its correlation coefficient, 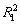, is 0.9384. According to the intercept of fitting curve, A′=2.62×10⁶. Hence, the power law constitutive equation for normal regression curve is obtained:

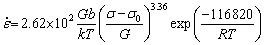  (18)

4 Discussion

4.1 Relationship between flow stress curves  and microstructural evolution during hot compression

As shown in Fig. 4, the flow stress curves exhibit different characteristics. It is our discovery that DRV dominates the process, and a certain work-hardening and a small amount of DRX softening exist during the thermal compression process. In other words, the flow curves exhibit horizontal DRV plateau, upward strain hardening, and downward DRX softening within the deformation temperatures and strain rates investigated. The horizontal DRV plateau results from the balance between the rearrangement and annihilation of dislocation. The upward strain hardening is related to the dynamic grain growth.  The downward DRX softening is related to the grain refinement at elevated temperatures. In addition, the yielding drop phenomenon was discovered, and the degree of yielding drop increases with the increase in strain rate and/or decrease in temperature. This result is closely related to the intense interaction between solute atmosphere and dislocations. Furthermore, the reason why the upward strain hardening is related to the dynamic grain growth is explained as follows. For fine-grained alloy, the grain interior is weaker than the grain boundary at room temperature, but the grain boundary is weaker than the grain interior at high temperature. Generally, at room temperature, coarsened grain leads to a decrease in grain boundary area, reduces the obstruction for dislocation movement, and results in a decrease in stress. However, the situation at high temperature is contrary to that at room temperature. Due to dynamic grain growth at high temperature, the number of dislocations inside a grain increases with increasing the grain size based on Eq. (10), the dislocation movement is obstructed, dislocation density increases, and hence the stress increases based on Eq. (9). That is the cause of strain hardening resulting from dynamic grain growth. Recently, the phenomenon that dynamic grain growth leads to strain-hardening was reported in superplastic commercial ZK30 magnesium  alloy [33] and superplastic CoCrFeNiMn high- entropy alloy [65]. Nevertheless, it is the first time that this phenomenon is discovered in this aluminum alloy.

As shown in Figs. 5-8, the abovementioned flow stress characteristics are confirmed by the microstructures. Little variation in grain size is consistent with the horizontal DRV curves. Dynamic grain growth is consistent with the upward strain-hardening curves. The strain- hardening curve at a strain rate of 1 s^-1 and 673 K  is an exception. Grain refinement in the microstructures is consistent with the downward DRX curves. In particular, it is suggested that continuous dynamic recrystallization followed by dynamic grain growth takes place at a temperature of 773 K and a strain rate of 0.001 s^-1.

4.2 Analysis of constitutive modeling

As shown in Section 3.4.1, Eqs. (9) and (10) are the hyperbolic sine constitutive equations containing dislocation variables. The scientific meaning of this modeling is that the dislocation density and number of dislocations can be obtained at different deformation temperatures and strain rates using both constitutive relationships. The newly established Arrhenius constitutive modeling or equations incorporating dislocation variables can be embedded in the control system of Castex and ECAP-Conform machine to display relevant information about temperature, velocity, forming force, grain size, number of dislocations, and dislocation density on the console. In this way the deformation process can be monitored and controlled. Furthermore, if this idea is extended to rolling, extrusion, forging, and other SPD processes, our constitutive modeling will bring about revolutionary changes in the control processes of corresponding machines. That is the scientific value and practical significance of this constitutive modeling.

As shown in Section 3.4.2, Eq. (18) is the normal power law constitutive equation with n=3.36. As shown in Fig. 14(b), the abnormal slope of n=8.20 resulting from power law breakdown at higher normalized strain rate and fixed normalized flow stress due to n≥7 is recognized as the occurrence of power law breakdown. This abnormality indicates that the flow stress saturates at higher strain rates, and the functional relation cannot be described as a single linear fit. Thus, due to the influence of the power law breakdown, the hyperbolic sine constitutive equation possesses higher predictability than the power law constitutive equation according to the comparison of the correlation coefficient of hyperbolic sine equation with that of the power law constitutive equation.

Finally, the stress exponent of 3.262 in the hyperbolic-sine equation is close to the stress exponent of 3.36 in the power law equation, indicative of the occurrence of dislocation viscous glide. It is a complicated problem that the dislocation viscous glide instead of grain boundary sliding occurs in this fine-grained alloy. Probable cause is that dynamic grain growth results in strain hardening, raises the stress exponent, and leads to the occurrence of dislocation viscous glide.

5 Conclusions

(1) Al-1.88Mg-0.18Sc-0.084Er alloy wires with a diameter of 8 mm were fabricated by Castex and ECAP-Conform. The grain size was refined from (58.48±3.95) μm in as-Castex state to (4.52±1.10) μm after the 4th-pass ECAP-Conform. The alloy wires were subjected to hot compression at temperatures of 673-793 K and strain rates of 0.001-10 s^-1.

(2) Flow stress curves exhibit horizontal dynamic recovery plateau, upward strain hardening, and downward dynamic recrystallization softening within the deformation temperatures and strain rates investigated; the yielding drop phenomenon was discovered, and the degree of yielding drop increased with the increase in strain rate and/or decrease in temperature.

(3) OM and EBSD results reveal that dynamic recovery is the dominant softening mechanism. Continuous dynamic recrystallization followed by dynamic grain growth takes place at a temperature of 773 K and a strain rate of 0.001 s^-1. XRD analysis reveals that this alloy consists of α(Al) solid solution phase, Mg₂Al₃, Al₁₂Mg₁₇, Al₂Sc, and Al₃Er intermetallic compounds.

(4) Hyperbolic sine constitutive equation incorporating number of dislocations inside a grain and dislocation density was presented for hot compression process. The estimated dislocation density is close to the experimental dislocation density determined by XRD line broadening approach while the estimated number of dislocations is approximately consistent with the TEM result at a temperature of 773 K and a strain rate of 0.001 s^-1. The stress exponent is 3.262, and the activation energy for deformation is 154.465 kJ/mol, indicating that dislocation viscous glide is the dominant deformation mechanism.

(5) A power law constitutive equation was established for hot compression process. The hyperbolic sine constitutive equation possesses higher predictability than the power law constitutive equation. This study can provide theoretical guidance for the understanding of the hot deformation process and for the design of Castex and ECAP-Conform machine.

Acknowledgments

The authors are grateful for the financial support from the Key Project of the National Natural Science Foundation of China (51334006).

References

[1] CAO Fu-rong, ZHOU Bi-jin, DING Xin, ZHANG Jian, XU Guang-ming. Mechanical properties and microstructural evolution in a superlight Mg-7.28Li-2.19Al-0.091Y alloy fabricated by rolling [J]. Journal of Alloys and Compounds, 2018, 745: 436-445.

[2] YANG Yan, PENG Xiao-dong, WEN Hai-ming, ZHENG Bao-long, ZHOU Yi-zhang, XIE Wei-dong, LAVERNIA E J. Influence of extrusion on the microstructure and mechanical behavior of Mg-9Li-3Al-xSr alloys [J]. Metallurgical and Materials Transactions A, 2013, 44(2): 1101-1113.

[3] SUN Y, AINDOW M, HEBERT R J, LANGDON T G, LAVERNIA E J. High-pressure torsion-induced phase transformations and grain refinement in Al/Ti composites [J]. Journal of Materials Science, 2017, 52(20): 12170-12184.

[4] SEMENOVA I P, POLYAKOV A V, POLYYAKOVA V V, GRISHINA Y F, HUANG Y, VALIEV R Z, LANGDON T G. Mechanical behavior and impact toughness of the ultrafine-grained Grade 5 Ti alloy processed by ECAP [J]. Materials Science and Engineering A, 2017, 696: 166-173.

[5] WATANABE C, MONZEN R, UEJI R, MIURA H. Strain-rate and temperature dependences of deformation behavior of AZ61Mg alloy processed by multi-directional forging under decreasing temperature conditions [J]. Metallurgical and Materials Transactions A, 2017, 48(11): 5368-5375.

[6] WU Hua-jie, WANG Tian-zi, WU Rui-zhi, HOU Le-gan, ZHANG Jing-huai, LI Xin-lin, ZHANG Mi-lin. Effects of annealing process on the interface of alternate α/β Mg-Li composite sheets prepared by accumulative roll bonding [J]. Journal of Materials Processing Technology, 2018, 254: 265-276.

[7] MA Z Y, MISHRA R S, MAHONEY M W, GRIMES R. Effect of friction stir processing on the kinetics of superplastic deformation in an Al-Mg-Zr alloy [J]. Metallurgical and Materials Transactions A, 2005, 36(6): 1447-1458.

[8] KOCH C C, LANGDON T G, LAVERNIA E J. Bulk nanostructured materials [J]. Metallurgical and Materials Transactions A, 2017, 48(11): 5181-5199.

[9] RAAB G J, VALIEV R Z, LOWE T C, ZHU Y T. Continuous processing of ultrafine grained Al by ECAP-Conform [J]. Materials Science and Engineering A, 2004, 382(1-2): 30-34.

[10] MURASHKIN M Y, MEDVEDEV A E, KAZYKHANOV V U, RAAB G I, OVID’KO I A, VALIEV R Z. Microstructure, strength, electrical conductivity and heat resistance of an Al-Mg-Zr alloy after ECAP-Conform and cold drawing [J]. Review of Advanced Materials Science, 2016, 47(1-2): 16-25.

[11] XU C, SCHROEDER S, BERBON P B, LANGDON T G. Principles of ECAP-Conform as a continuous process for achieving grain refinement: Application to an aluminum alloy [J]. Acta Materialia, 2010, 58(4): 1379-1386.

[12] CAO Fu-rong, WEN Jing-lin, DING Hua, WANG Zhao-dong, YU Chuan-ping, XIA Fei. Extrusion force analysis of aluminum pipe fabricated by CASTEX using expansion combination die [J]. Transactions of Nonferrous Metals Society of China, 2014, 24(11): 3621-3631.

[13] CAO Fu-rong, WEN Jing-lin, DING Hua, WANG Zhao-dong, LI Ying-long, GUAN Ren-guo, HOU Hui. Force analysis and experimental study of aluminum and Al-5%Ti-1%B alloy continuous extrusion forming process [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(1): 201-207.

[14] GUAN Ren-guo, JIN Hong-mei, JIANG Wen-sen, WANG Xiang, WANG Yu-xiang, LI Zheng, ZHANG Jian, LIU Hui-nan. Quantitative contributions of solution atoms, precipitates and deformation to microstructures and properties of Al-Sc-Zr alloys [J]. Transactions of Nonferrous Metals Society of China, 2019, 29(5): 907-918.

[15] TANG Lei, PENG Xiao-yan, HUANG Ji-wu, MA Ai-bin, DENG Ying, XU Guo-fu. Microstructure and mechanical properties of severely deformed Al-Mg-Sc-Zr alloy and their evolution during annealing [J]. Materials Science and Engineering A, 2019, 754: 295-308.

[16] PENG Jian, WANG Yong-jian, ZHONG Li-ping, PENG Long-fei, PAN Fu-sheng. Hot deformation behavior of homogenized Al-3.2Mg-0.4Er aluminum alloy [J]. Transactions of Nonferrous Metals Society of China, 2016, 26(4): 945-955.

[17] MALOPHEYEV S, MIRONOV S, KULITSKIY V, KAIBYSHEV R. Friction-stir welding of ultra-fine grained sheets of Al-Mg-Sc-Zr alloy [J]. Materials Science and Engineering A, 2015, 624: 132-139.

[18] CAO Xiao-wu, XU Guo-fu, DUAN Yu-lu, YIN Zhi-min, LU Li-ying, WANG Ying-jun. Achieving high superplasticity of a new Al-Mg-Sc-Zr alloy sheet prepared by a simple thermal–mechanical process [J]. Materials Science and Engineering A, 2015, 647: 333-343.

[19] WANG K, LIU F C, XUE P, WANG D, XIAO B L, MA Z Y. Superplastic constitutive equation including percentage of high-angle grain boundaries as a microstructural parameter [J]. Metallurgical and Materials Transactions A, 2016, 47(1): 546-559.

[20] KIM B H, SEYED SALEHI M, NOURI A, MOHEBI M S, HA S H, YOON Y O, LIM H K, KIM S K, EISAABADI B G. Role of Ca in hot compression behavior and microstructural stability of AlMg5 alloy during homogenization [J]. Transactions of Nonferrous Metals Society of China, 2020, 30(3): 571-581.

[21] DAI Qing-song, DENG Yun-lai, TANG Jian-guo, WANG Yu. Deformation characteristics and strain-compensated constitutive equation for AA5083 aluminum alloy under hot compression [J]. Transactions of Nonferrous Metals Society of China, 2019, 29(11): 2252-2261.

[22] CHEN Xi-hong, FAN Cai-he, HU Ze-yi, YANG Jian-jun, GAO Wen-li. Flow stress and dynamic recrystallization behavior of Al-9Mg-1.1Li-0.5Mn alloy during hot compression process [J]. Transactions of Nonferrous Metals Society of China, 2018, 28(12): 2401-2409.

[23] SUN Yuan-wei, PAN Qing-lin, WANG Wei-yi, LI An-de, SONG Wen-bo. Microstructural evolution and constitutive analysis combined with weight optimization method of Al-7.82Zn-1.96Mg-2.35Cu-0.11Zr alloy during hot deformation [J]. Journal of Alloys and Compounds, 2018, 732: 902-914.

[24] ZHAO Jiu-hui, DENG Yun-lai, TAN Jia, ZHANG Jin. Effect of strain rate on the recrystallization mechanism during isothermal compression in 7050 aluminum alloy [J]. Materials Science and Engineering A, 2018, 734: 120-128.

[25] WANG Xiang-dong, PAN Qing-lin, XIONG Shang-wu, LIU Li-li, SUN Yuan-wei, WANG Wei-yi. Prediction on hot deformation behavior of spray-formed 7055 aluminum alloy via phenomenological models [J]. Transactions of Nonferrous Metals Society of China, 2018, 28(8): 1484-1494.

[26] ZHANG Cun-sheng, WANG Cui-xue, GUO Ran, ZHAO Guo-qun, CHEN Liang, SUN Wen-chao, WANG Xie-bin. Investigation of dynamic recrystallization and modeling of microstructure evolution of an Al-Mg-Si aluminum alloy during high temperature deformation [J]. Journal of Alloys and Compounds, 2019, 773: 59-70.

[27] QUAN Guo-zheng, SHI Rui-ju, ZHAO Jiang, LIU Qiao, XIONG Wei, QIU Hui-min. Modeling of dynamic recrystallization volume fraction evolution for AlCu4SiMg alloy and its application in FEM [J]. Transactions of Nonferrous Metals Society of China, 2019, 29(6): 1138-1151.

[28] LIU Lei, WU Yun-xin, GONG Hai, WANG Kai. Modification of constitutive model and evolution of activation energy on 2219 aluminum alloy during warm deformation process [J]. Transactions of Nonferrous Metals Society of China, 2019, 29(3): 448-459.

[29] SAKAI T, BELYAKOV A, KAIBYSHEV R, MIURA H, JONAS J J. Dynamic and post dynamic recrystallization under hot, cold and severe plastic deformation conditions [J]. Progress in Materials Science, 2014, 60: 130-207.

[30] LIN Y C, CHEN X M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working [J]. Materials and Design, 2011, 32(4): 1733-1759.

[31] ZHONG Li-wei, GAO Wen-li, FENG Zhao-hui, LU Zheng, MAO Guo-ling. Microstructure characteristics and constitutive modeling for elevated temperature flow behavior of Al-Cu-Li X2A66 alloy [J]. Journal of Materials Research, 2018, 33(8): 912-922.

[32] MIRZADEH H. A simplified approach for developing constitutive equations for modeling and prediction of hot deformation flow stress [J]. Metallurgical and Materials Transactions A, 2015, 46(9): 4027-4037.

[33] ALVAREZ-LEAL M, OROZCO-CABALLERO A, CARRENO F, RUANO O A. Superplasticity in a commercially extruded ZK30 magnesium alloy [J]. Materials Science and Engineering A, 2018, 710: 240-244.

[34] CAO Fu-rong, ZHU Xiao-tong, WANG Shun-cheng, SHI Lu, XU Guang-ming, WEN Jing-lin. Quasi-superplasticity of a banded-grained Al-Mg-Y alloy processed by continuous casting-extrusion [J]. Materials Science and Engineering A, 2017, 690: 433-445.

[35] WU H, WEN S P, HUANG H, GAO K Y, WANG W, NIE Z R. Hot deformation behavior and processing map of a new type Al-Zn-Mg-Er-Zr alloy [J]. Journal of Alloys and Compounds, 2016, 685: 869-880.

[36] WU H, WEN S P, HUANG H, WU X L, GAO K Y, WANG W, NIE Z R. Hot deformation behavior and constitutive equation of a new type Al-Zn-Mg-Er-Zr alloy during isothermal compression [J]. Materials Science and Engineering A, 2016, 651: 415-424.

[37] YAN J, PAN Q L, LI B, HUANG Z Q, LIU Z M, YIN Z M. Research on the hot deformation behavior of Al-6.2Zn- 0.70Mg-0.3Mn-0.17Zr alloy using processing map [J]. Journal of Alloys and Compounds, 2015, 632: 549-557.

[38] CHAMANFA A, ALAMOUDI M T, NANNINGA N E, MISIOLEK W Z. Analysis of flow stress and microstructure during hot compression of 6099 aluminum alloy (AA6099) [J]. Materials Science and Engineering A, 2019, 743: 684-696.

[39] KIM W J, JEONG H T. Pronounced yield drop phenomenon at high temperatures in Al-Mg alloys with high contents of Mg (5-13 wt%) [J]. Materials Science and Engineering A, 2019, 743: 590-596.

[40] ZHOU L, CUI C, WANG Q Z, LI C, XIAO B L, MA Z Y. Constitutive equation and model validation for a 31 vol.% B₄C_p/6061Al composite during hot compression [J]. Journal of Materials Science and Technology, 2018, 34(10): 1730-1738.

[41] GOETZ R L, SEMIATIN S L. The adiabatic correction factor for deformation heating during the uniaxial compression test [J]. Journal of Materials Engineering and Performance, 2001, 10(6): 710-717.

[42] DING S, KHAN S A, YANAGIMOTO J. Constitutive descriptions and microstructure evolution of extruded A5083 aluminum alloy during hot compression [J]. Materials Science and Engineering A, 2018, 728: 133-143.

[43] CHEN Gao-jin, CHEN Liang, ZHAO Guo-qun, ZHANG Cun-sheng, CUI Wei-chao. Microstructure analysis of an Al-Zn-Mg alloy during porthole die extrusion based on modeling of constitutive equation and dynamic recrystallization [J]. Journal of Alloys and Compounds, 2017, 710: 80-91.

[44] LIU Shu-hui, PAN Qing-lin, LI Hang, HUANG Zhi-qi, LI Kuo, HE Xin, LI Xin-yu. Characterization of hot deformation behavior and constitutive modeling of Al-Mg- Si-Mn-Cr alloy [J]. Journal of Materials Science, 2019, 54(5): 4366-4383.

[45] MOHRI T, MABUCHI M, NAKAMURA M, ASAHINA T, IWASAKI H, AIZAWA T, HIGASHI K. Microstructural evolution and superplasticity of rolled Mg-9Al-1Zn [J]. Materials Science and Engineering A, 2000, 290(1-2): 139-144.

[46] SELLARS C M, MCTEGART W J. On the mechanism of hot deformation [J]. Acta Metallurgica, 1966, 14: 1136-1138.

[47] SUN Y, YE W H, HU L X. Constitutive modeling of high-temperature flow behavior of Al-0.62Mg-0.73Si aluminum alloy [J]. Journal of Materials Engineering and Performance, 2016, 25(4): 1621-1630.

[48] LIU Yang, GENG Cong, ZHU Yun-ke, PENG Jin-feng, XU Jun-rui. Hot deformation behavior and intrinsic workability of carbon nanotube-aluminum reinforced ZA27 composites [J]. Journal of Materials Engineering and Performance, 2017, 26(4): 1967-1977.

[49] LEE S W, YEH J W. Superplasticity of 5083 alloys with Zr and Mn additions produced by reciprocating extrusion [J]. Materials Science and Engineering A, 2007, 460-461: 409-419.

[50] ZENER C, HOLLOMON J H. Effect of strain rate upon plastic flow of steel [J]. Journal of Applied Physics, 1944, 15(1): 22-32.

[51] CAO Fu-rong, XIA Fei, XUE Guo-qiang. Hot tensile deformation behavior and microstructural evolution of a Mg-9.3Li-1.79Al-1.61Zn alloy [J]. Materials and Design, 2016, 92: 44-57.

[52] LANGDON T G, MOHAMED F A. A new type of deformation mechanism map for high-temperature creep [J]. Materials Science and Engineering A, 1978, 32(2): 103-112.

[53] FROST H J, ASHBY M F. Deformation mechanism maps [M]. Oxford: Pergamon Press, 1982.

[54] PHANI K K, SANYAL D. The relations between the shear modulus, the bulk modulus and Young’s modulus for porous isotropic ceramic materials [J]. Materials Science and Engineering A, 2008, 490(1-2): 305-312.

[55] TALEFF E M, HECTOR L G, BRADLEY J R, VERMA R, KRAJEWSKI P E. The effect of stress state on high- temperature deformation of fine-grained aluminum– magnesium alloy AA5083 sheet [J]. Acta Materialia, 2009, 57(9): 2812-2822.

[56] XU Xiao-jing, SHAO Hong-hong, GAO Jian-chang, CHEN Kang-min, CHENG Xiao-nong. Effect of SiC film on tensile properties of nanostructured Ti produced by compressive deformation at liquid-nitrogen temperature [J]. Materials Science and Engineering A, 2008, 493(1-2): 195-201.

[57] XU Xiao-jing, CAO Jin-qi, CHENG Xiao-nong, MO Ji-ping. Tensile properties of 2024 Al alloy processed by enhanced solid-solution and equal-channel angular pressing [J]. Transactions of Nonferrous Metals Society of China, 2006, 16(S): s1541-s1544.

[58] YOUSSEF K M, SCATTERGOOD R O, MURTY K L, KOCH C C. Nanocrystalline Al-Mg alloy with ultrahigh strength and good ductility [J]. Scripta Materialia, 2006, 54(2): 251-256.

[59] ZHAO Y H, LIAO X Z, JIN Z, VALIEV R Z, ZHU Y T. Microstructures and mechanical properties of ultrafine grained 7075 Al alloy processed by ECAP and their evolutions during annealing [J]. Acta Materialia, 2004, 52(15): 4589-4599.

[60] GASHTI S O, FATTAH-ALHOSSEINI A, MAZAHERI Y, KESHAVARZ M K. Effects of grain size and dislocation density on strain hardening behavior of ultrafine grained AA1050 processed by accumulative roll bonding [J]. Journal of Alloys and Compounds, 2016, 658: 854-861.

[61] WANG S C, ZHU Z, STARINK M J. Estimation of dislocation densities in cold rolled Al-Mg-Cu-Mn alloys by combination of yield strength data, EBSD and strength models [J]. Journal of Microscopy, 2005, 217: 174-178.

[62] LANGDON T G. A unified approach to grain boundary sliding in creep and superplasticity [J]. Acta Metallurgica et Materialia, 1994, 42(7): 2437-2443.

[63] KASSNER M E, PEREZ-PRADO M T. Five-power-law creep in single phase metals and alloys [J]. Progress in Materials Science, 2000, 45(1): 1-102.

[64] TALEFF E M, RUANO O A , WOLFENSTINE J, SHERBY O D. Superplastic behavior of a fine-grained Mg-9Li materials at low homologous temperature [J]. Journal of Materials Research, 1992, 7(8): 2131-2135.

[65] SHAHMIR H, HE Jun-yang, LU Zhao-ping, KAWASAKI M, LANGDON T G. Evidence for superplasticity in a CoCrFeNiMn high-entropy alloy processed by high-pressure torsion [J]. Materials Science and Engineering A, 2017, 685: 342-348.

Al-1.88Mg-0.18Sc-0.084Er合金的热压缩组织演变、流动应力与本构建模

曹富荣^1,2,3，尹 斌⁴，刘斯元¹，石 路¹，王顺成⁵，温景林¹

1. 东北大学 材料科学与工程学院，沈阳 110819；

2. 东北大学 轻质结构材料辽宁省重点实验室，沈阳 110819；

3. 东北大学 轧制与连轧自动化国家重点实验室，沈阳 110819；

4. 芜湖凯翼汽车有限公司，芜湖 241000；

5. 广东工业技术研究院 材料加工与成形研究所，广州 510650

摘  要：为了研究合金热压缩行为与显微组织演变，采用连续铸挤与等通道转角挤压-连续挤压方法制备细晶Al-1.88Mg-0.18Sc-0.084Er(质量分数，%)铝合金线材并在温度为673~793 K与应变速率为0.001~10 s^-1条件下研究其热压缩行为。采用光学显微镜、X射线衍射仪、透射电镜和电子背散射衍射仪对合金的显微组织进行表征；采用热压缩模拟试验机获得其流动应力。显微组织演变与流动应力曲线表明，动态回复为合金主要的软化机理；在773 K 和0.001 s^-1条件下发生连续动态再结晶随后动态晶粒长大；发现屈服点下降现象。提出含位错变量的双曲正弦本构方程并建立幂律本构方程。应力指数为3.262，变形激活能为154.465 kJ/mol，表明位错黏性滑移为合金主要的变形机理。

关键词：Al-Mg合金；等通道转角挤压-连续挤压；热压缩；显微组织；流动应力；本构方程

 (Edited by Wei-ping CHEN)

Corresponding author: Fu-rong CAO; Tel: +86-15998161852; E-mail: cfr-lff@163.com, caofr@smm.neu.edu.cn

DOI: 10.1016/S1003-6326(20)65478-4

1003-6326/ 2021 The Nonferrous Metals Society of China. Published by Elsevier B.V. & Science Press