DOI: 10.11817/j.issn.1672-7207.2015.07.035
三轴试样高径比对试验影响的颗粒流数值模拟
陈镠芬1, 2,朱俊高1, 2,殷建华3
(1. 河海大学 岩土力学与堤坝工程教育部重点实验室,江苏 南京,210098;
2. 河海大学 岩土工程科学研究所,江苏 南京,210098;
3. 香港理工大学 土木工程系,中国 香港)
摘要:基于离散元软件PFC3D,通过编制可破碎的颗粒簇单元,模拟三轴试验中不同高径比试样应力应变特性的差异,通过比较强度和变形参数差异探讨适合粗粒土的高径比。研究结果表明:高径比越小,试验得到的内摩擦角越大,围压越大,由于颗粒破碎导致的内摩擦角越小;满足莫尔-库仑准则破坏面的最小高径比随着围压的增加而减小,但都大于现在室内试验常用的高径比;峰值强度随着高径比的增加而减小,随着围压的增大,不同高径比之间峰值强度相对误差减小;割线模量与高径比呈折线形关系;不同高径比之间割线模量的差异随高径比范围的不同而不同,且最小高径比的割线模量与现在室内试验常用高径比的割线模量在低围压下差异较大。依据模拟结果,认为粗粒土的三轴试样高径比应大于2.5。
关键词:粗粒土;高径比;PFC3D软件;峰值强度;割线模量
中图分类号:TU411 文献标志码:A 文章编号:1672-7207(2015)07-2643-07
Numerical simulations of mechanical characteristics of coarse grained soil with different aspect ratios of tri-axial test
CHEN Liufen1, 2, ZHU Jungao1, 2, YIN Jianhua3
(1. Key Laboratory of Geomechanics and Embankment Engineering, Ministry of Education,
Hohai University, Nanjing 210098, China;
2. Geotechnical Research Institute, Hohai University, Nanjing 210098, China;
3. Department of Civil and Structure Engineering, The HongKong Polytechnic University, Hong Kong, China)
Abstract: The influences of mechanical characteristics and particle breakage with different aspect ratios were analysed based on DEM software PFC3D, and cluster element considering of particle breakage was developed. Meanwhile, the aspect ratio suitables to coarse grained soil was discussed by means of strength and deformation parameter. The results show that the smaller the aspect ratio, the bigger the friction angle, and that the bigger the pressure, the smaller the friction angle as a result of particle breakage. The minimum aspect ratio that satisfies Mohr-Coulomb criterion decreases with the increase of pressure, but each of them is larger than existing laboratory test aspect ratio. The peak strength decreases with the increase of aspect ratio, and so does relative error of the peak strength. The relationship between secant modulus and aspect ratio shows that the differences of secant modulus vary from aspect ratio to aspect ratio, and that there exists significant difference between the minimum aspect ratio and existing one. So, for the coarse grained soil, the aspect ratio should be larger than 2.5.
Key words: coarse grained soil; aspect ratio; PFC3D software; peak strength; secant modulus
三轴试验因其明确的应力条件和可控的排水条件等优点是目前土工室内试验中最主要的试验,应用十分广泛。在实际工程中,三轴试验常用来测定土体的强度和变形参数,精确性对土工结构变形及稳定性分析结果有直接影响。然而,除了试验材料自身离散性等影响因素外,试验条件也是影响试验结果的一个重要因素,比如,尺寸效应就是一个需要考虑的问题。尺寸效应研究较多在缩尺效应或是颗粒粒径与试样直径的对应关系[1-4],而对于试样高径比的研究相对较少。目前,国内外土工试验规范一般规定试样高度是试样直径的2.0~2.5倍,而事实上,很多三轴仪取用的试样高径比为2.0。按照莫尔-库仑破坏准则,黏性土试样高径比可以为2.0。但是,对砂土或堆石料等粗粒土,其摩擦角较大,甚至超过40°,按照莫尔-库仑准则,其破坏面与大主应力面夹角为45°+φ/2,则破坏面就切割到试样帽或试样底座,反之,这时的破坏面不符合莫尔-库仑准则,或者说这不是真正最危险滑动面。若试样高径比大,则会形成与大主应力面夹角为45°+φ/2的破坏面,试验测定的性质是否随高径比增大而变化?另外,目前对于尺寸效应研究通常是通过试验总结分析[5-9]。然而,由于土料和制样的随机性,即使过程再统一,室内三轴试验数据仍然具有很大离散性,规律性较差。相反,数值试验可以根据试验目的灵活地选择试验条件及控制因素,能保证统一的颗粒组合,使试验和数据处理更为灵活,能较充分的体现规律性,突破了常规试验仪器设备能力、试验条件上的局限性,是科学研究中重要的辅助手段。颗粒破碎是粗粒土试验中的一个重要现象,颗粒破碎导致内摩擦角随围压的增大而减小,呈明显的非线性现象。近年来,众多学者采用试验和数值模拟对颗粒破碎进行了深入研究,在数值模拟研究中PFC程序被广泛用来模拟土的力学特性和颗粒破碎现象[10-14]。但针对颗粒破碎多是采用二维的圆盘,对三维的情况研究较少。一方面,三维模型引起较多的颗粒数量,使计算机无法计算;另一方面,颗粒破碎会引起孔隙率的变化,如何定量这部分孔隙还有待进一步考虑,虽然人们对此进行了探讨,但都局限于二维情况[10]。显然,用二维模拟与实际的三维试验有着本质的区别,用二维模拟进行三维的定量研究不具有参考价值。鉴于此,本文作者以双江口堆石坝的坝壳堆石料的试验数据为依据,采用离散元软件PFC3D中的颗粒簇单元(Cluster),用fish语言开发一种形成颗粒簇的新方法,建立可破碎的颗粒簇,研究不同围压下、不同高径比对应力应变强度特性的影响,并探讨适合粗粒土的高径比。
1 三轴数值试样制备及细观参数设置
本文采用6组试样,其高度×直径分别为10 cm× 10 cm,15 cm×10 cm,20 cm×10 cm,25 cm×10 cm,30 cm×10 cm和35 cm×10 cm,相应高径比分别为1.0,1.5,2.0,2.5,3.0和3.5,分别用方案1~6表示。试验围压分别为200,500,800和1 200 kPa。为了节约篇幅,这里只给出试样高度×直径为20 cm×10 cm的建模过程。
1.1 数值试样参数及本构模型的选取
系统的力学特征和力学响应主要通过颗粒间简单的接触本构关系来模拟。每一接触位置包括接触刚度模型、滑动模型和黏结模型[15]3部分。
对于任意2个有接触关系的球使用不同接触刚度模型是不允许的, 在PFC程序中Hertz模型不能定义拉张应力,与任何类型的黏结不兼容,因此本文采用线性接触刚度模型,通过2个接触实体(球-球或球-墙)的法向和切向接触刚度kn和ks定义。
堆石料是颗粒间不存在黏结力的散粒体材料,一般采用滑动模型模拟颗粒之间的滑动,是通过两接触体间最小摩擦因数fc定义的。
本文选取接触黏结模型模拟颗粒破碎,主要由法向黏结强度Fcn和切向黏结强度Fcs决定。
1.2 颗粒簇单元的建立
圆形颗粒是组成试样最基本的单元。在PFC3D中单个颗粒是不能破碎的,且圆形颗粒不能体现实际颗粒的形状特性。因此,本文运用PFC3D里面的颗粒簇(Cluster)功能编写程序,形成一个能反映形状和实现颗粒破碎的聚粒。生成颗粒簇的方法是通过确定一系列母颗粒,然后将相邻的颗粒加入到簇之中,直到所有相邻的颗粒都加进去或颗粒数达到最大值,同时判断各粒组的含量是否满足级配曲线的要求,本文采用的级配曲线如图1所示。这种方法一方面保证了颗粒簇的最大粒径满足三轴试验要求,另一方面使生成颗粒在可控范围之内,大大提高了计算机的效率。
1.3 数值试样制备
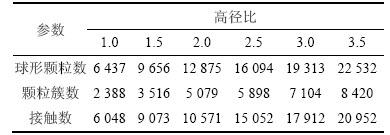
三轴试验数值模拟是通过对2个加载压盘施加速度从而达到给颗粒集合体施加竖向压力的目的,然后通过数值伺服系统控制墙体的移动速度使墙体的应力达到规定的应力,并保持围压的稳定。具体建模过程分为以下4个步骤:1) 建立圆柱形墙体和上下加载压盘来分别模拟室内试验的橡皮膜和试样帽或试样底座,并设定摩擦因数模拟加载压盘与试样的接触状态;2) 在墙体内根据粒径范围和孔隙率按均匀分布随机生成颗粒,颗粒粒径范围为1.0~3.5 mm,颗粒密度为2 000 kg/m3,初始孔隙率为0.3;3) 编制fish程序,按照级配曲线生成颗粒簇,如图2和图3所示,生成的圆形颗粒数量、颗粒簇数量及颗粒间接触数量见表1;4) 由伺服控制系统对试样施加围压并保持恒定,施加围压后加载剪切速度,开始试验,直至轴向应变达到15%后停止试验。
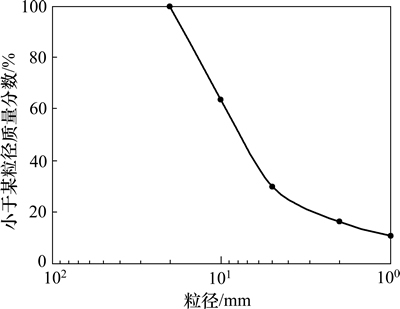
图1 粗粒料级配曲线
Fig.1 Gradation curve of rock fill

图2 考虑颗粒破碎的数值试样
Fig. 2 Numerical sample considering particle breakage
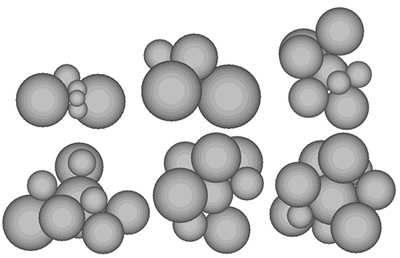
图3 不同颗粒簇组合
Fig. 3 Groups of cluster element
表1 不同高径比试样的颗粒数及接触数
Table 1 Number of particles and contact of different aspect ratios 个
1.4 细观参数标定
为使1.1节确定的细观参数能够反映实际土体的真实行为,需要通过宏观力学参数的反分析得到细观参数。本文选用双江口试验的应力-应变曲线作为标定曲线,经过大量的试算,最终确定的一组颗粒细观力学参数见表2。室内试验和数值模拟试验的应力-应变曲线对比见图4,宏观参数对比见表3,表3中E50为割线弹性模量,是试样强度为峰值强度一半时的应力与应变的比值,通常称为变形模量,用以表示土的变形特性。
表2 颗粒细观力学参数
Table 2 Micro parameters of particle
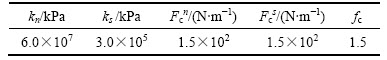
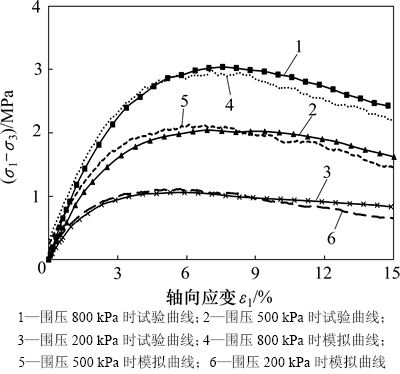
图4 三轴试验与数值模拟试验应力-应变曲线对比图
Fig. 4 Stress and strain curves of triaxial compression tests and numerical simulations
表3 室内试验与PFC3D模拟试验的宏观参数对比
Table 3 Macro parameters of triaxial compression tests and numerical simulations
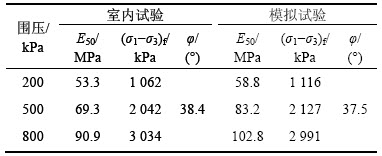
鉴于球颗粒与实际材料的形状、大小、性质相差较大,颗粒之间的咬合作用大大减弱, 因此,数值模拟结果很难与室内试验结果达到完全一致。由图4和表3可以看出:该数值模型与室内试验的应力-应变曲线有一定程度的偏差,但变化趋势基本一致,两者的峰值强度和内摩擦角也较接近,相对误差均小于5%,由此可以判断该组模型参数能够反映双江口堆石料的宏观应力-应变特性,能代表室内试验进行进一步研究。
2 数值试验结果分析
根据莫尔-库仑准则,破坏面与大主应力面夹角为45°+φ/2,若高径比太小,在试样内部就不能形成对应的破坏面,因此存在1个最小高径比正好满足莫尔-库仑准则,如图5所示。

图5 最小高径比示意图
Fig. 5 Sketch map of the minimum aspect ratio
基于第1节建立的试样,进行了不同围压下三轴试验的模拟。受颗粒破碎的影响,围压不同将导致粗粒土内摩擦角不同,从而,试样最小高径比也不同。所以,本文通过整理不同围压下内摩擦角与高径比的关系,确定不同围压下的最小高径比,并分析高径比对粗粒土强度和变形的影响。表4所示为不同方案三轴试验得到的内摩擦角,表5所示为根据内摩擦角计算的满足莫尔-库仑准则破坏面的最小高径比。
表4 不同方案试样的内摩擦角
Table 4 Friction angles of different schemes (°)
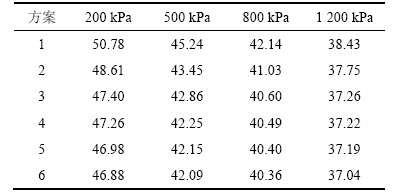
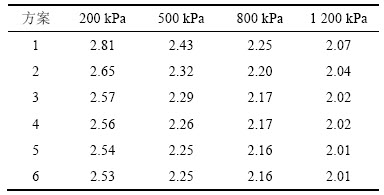
表5 不同围压下满足莫尔-库仑准则破坏面的高径比
Table 5 Aspect ratios suit for Mohr-Coulomb criterion of different confining pressures
由表4可以看出:不同方案之间的内摩擦角有差异,差异程度随围压的不同而不同。高径比越小,内摩擦角越大,尤其是高径比为1.0和1.5的情况,内摩擦角与其他高径比的内摩擦角差距较大。本文作者认为其原因是:一是因为高径比较小时,破坏面会切割到加载压盘,加载压盘影响了破坏面形成,从而导致内摩擦角增大;二是加载压盘与颗粒间有摩擦力,影响了试样的内应力,从而进一步增加了内摩擦角。随着高径比增加,破坏面逐渐不受加载压盘的影响,内摩擦角减小,且不同高径比之间内摩擦角差异较小,如方案4~6所示。本文作者认为产生这种微小的差异是较大的高径比引起的,高径比大会导致试样的不稳定性,使内摩擦角减小;随着围压的增加,试样内部颗粒破碎越来越显著,导致同一高径比试样的内摩擦角逐渐减小,减小幅度较大。
内摩擦角随围压的变化引起了最小高径比在不同围压下的差异,围压越大,最小高径比越小。同时,在高围压下,不同方案之间高径比的差异越小,如表5所示。从表5可以看出:通过内摩擦角计算的高径比与原有的高径比是矛盾的,因此,选择1个合理的高径比对试验的准确性至关重要。
针对本文研究的4种围压,室内试样的最小高径比分别要达到2.6,2.3,2.2和2.1才能满足莫尔-库仑准则。基于此,本文围绕各围压的最小高径比,研究了不同高径比对粗粒土强度、变形的影响。为便于表述,将最小高径比的情况定为方案7。
2.1 高径比对应力-应变强度的影响
图6所示为不同围压下方案1~6的应力-应变曲线,表6所示为对应的峰值强度,表6中相对误差e指不同方案峰值强度差的相对百分数,即
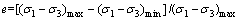
由图6可以看出:各个围压下,不同方案的应 力-应变曲线趋势相同,且随着高径比的减小曲线逐步上扬。特别是高径比为1.0和1.5的情况,在轴向应变达到4%后,其应力-应变曲线明显上升,而其余4种方案的应力-应变曲线虽然在低围压下比较分散,但随着围压的增加,曲线越来越集中。尤其是当高径比大于等于2.5,围压到达800 kPa时,3种方案的应力应变曲线趋于一致。同时,从图6还可以看出:高径比越小,应力-应变曲线达到峰值强度时的应变越大。另外,受颗粒破碎程度的影响,达到峰值强度前各方案的应力-应变曲线比较光滑,峰值强度后曲线的波动性增强,围压越大,波动幅度越大。
表6 各围压下不同方案试样的峰值强度
Table 6 Peak strength of different schemes kPa
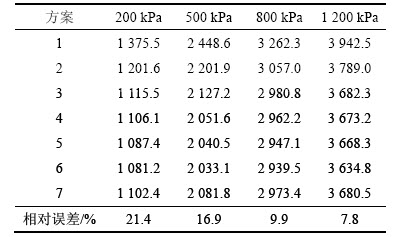
从表6可以看出:高径比对试样峰值强度影响显著,峰值强度随着高径比的增加而减小,这是由于高径比较小时,试样在剪切过程中受端部加载压盘的影响较大,这是一种虚假的高。在低围压如200 kPa下,不同高径比的峰值强度差最大,占最大峰值强度的21.4%。随着围压的增大,加载压盘的影响逐渐减小,不同高径比之间的峰值强度差逐渐减小,当围压为1 200 kPa时,峰值强度相对误差减小到7.8%。
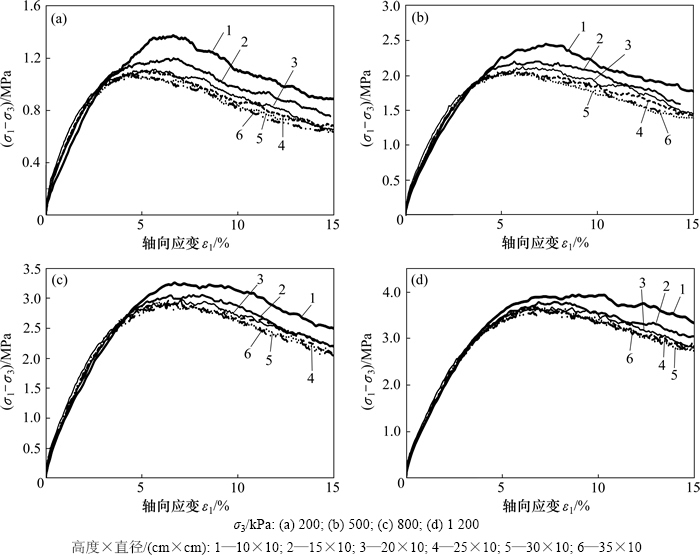
图6 各围压下不同方案的应力-应变曲线
Fig. 6 Stress and strain curves of different schemes
本文根据莫尔-库仑准则计算出了各围压下的最小高径比,并通过与其相邻方案的峰值强度插值得到方案7的峰值强度,如表6所示。方案7与其他方案峰值强度的相对误差如表7所示。
表7 方案7与其他方案峰值强度的相对误差
Table 7 Relative error of peak strength among scheme 7 and other schemes %
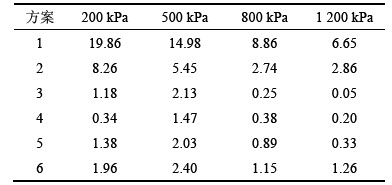
由表7可以看出:高径比越小,与方案7峰值强度的相对误差就越大;围压越小,相对误差也越大。如当围压为200 kPa时,方案7的峰值强度与方案1的峰值强度相对误差达到19.86%。随着高径比的增大,加载压盘对形成破坏面的影响减小,相对误差明显减小,与方案4的相对误差仅为0.34%。随着高径比的进一步增大,相对误差又有所增大,当高径比为3.5时,相对误差达到2.40%。产生这种原因是高径比不同导致内部颗粒数及排列不同,因此,当高径比大于最小高径比时,虽然加载压盘对形成破坏面已没有影响,但在峰值强度上会有些差异。在其他围压下,最小高径比与各高径比的相对误差的变化规律一致,结果如表7所示。
由表7还可见:对于高径比小于2.5的试样受两端加载压盘的影响明显,易造成强度增加过多,影响了试验的准确性。而对于高径比大于等于3的试样,虽然峰值强度相差较小,但试样高了稳定性变差,且制样困难,仪器高度增加,增加了试验的难度。因此,当摩擦角较大时,高径比最好大于2.5,一方面,满足了莫尔-库仑准则,提高了试验精度;另一方面,对制样的影响小,试样稳定性高,具有可操作性。
2.2 高径比对变形的影响
由图6可以看出:低围压下,高径比越小,初始切线模量越小,这种差异随着围压的增加而减小。
对于像金属等具有大范围线弹性行为的材料来说,用初始切线模量表示其变形特性是符合实际的,但是粗粒土是非线性材料,可采用割线模量表示其变形与加载之间的关系。本文采用割线弹性模量E50来分析不同高径比试样的变形特性差异。
图7所示为各高径比与E50的对应关系;表8所示为各围压下的最小高径比与相邻高径比割线模量的相对误差。
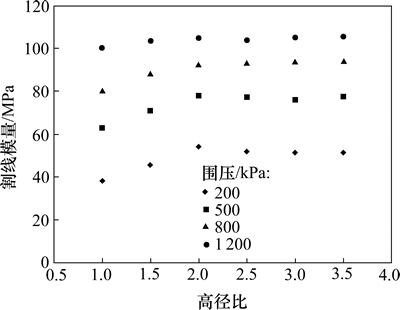
图7 不同围压试样的割线模量与高径比的关系
Fig. 7 Relationships between secant modulus and aspect ratio
由图7可以看出:随围压的不同,割线模量与高径比呈不同的线形关系。当围压小于1 200 kPa时,高径比为1.0~2.0的割线模量随着高径比的增大等斜率增加,围压越小,斜率越大;当高径比为2.0时,割线模量达到最大值,之后割线模量随着高径比的增大略有变化,变化较平缓;当围压大于1 200 kPa时,高径比对割线模量的影响很小,几乎呈一条平缓的直线。
由图6可以看出:在应力-应变曲线达到峰值强度前,且高径比小于等于2.0时,应力-应变曲线各点的切线斜率随着高径比的增大而增大,各高径比的峰值强度变化幅度小于应变的变化幅度,因此,割线模量随着高径比的增大而增大;当高径比大于2.0时,各方案峰值强度前的应力-应变曲线几乎接近,且峰值强度也相差较小,所以,相应的割线模量相差较小。
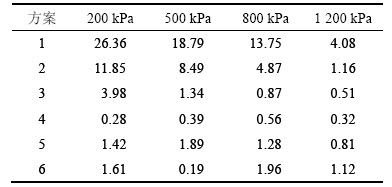
针对各围压下的最小高径比,整理了方案7与其他方案割线模量在各围压下的相对误差,如表8所示。
由表8可以看出:方案7的割线模量与方案1和2的割线模量相对误差较大,低围压下最大达到26.36%,高围压下达到4.08%;随着高径比的增加,方案7与其他方案的割线模量相对误差逐渐减小;对于方案3,在低围压下与方案7的相对误差较大。从本文研究的4个围压考虑,方案4(即高径比为2.5)与方案7的割线模量较接近。
表8 方案7与其他方案割线模量的相对误差
Table 8 Relative error of secant modulus among scheme 7 and other schemes %
针对粗粒土,现在室内试验中主要采用的高径比仍是2.0,因此,从变形参数的角度考虑这是不合适的,应采用大于2.5的高径比。
3 结论
1) 内摩擦角随高径比的增大而减小,减小幅度亦随着高径比的增大而减小。根据莫尔-库仑准则破坏面计算的最小高径比随着围压的不同而不同。
2) 峰值强度随着高径比的增加而减小,随着围压的增大,不同高径比之间峰值强度相对误差减小。高径比越小,最小高径比与其峰值强度的相对误差越大。
3) 割线模量与高径比呈折线形关系,不同高径比之间割线模量变化幅度随高径比的不同而不同。各围压下最小高径比的割线模量与高径比为2.5的割线模量较接近。
4) 根据本文的研究成果,对于摩擦角较大的粗粒土,在进行三轴试验时,现行采用的2.0~2.5的高径比不能真正反映粗粒土应力应变特性,建议采用大于2.5的高径比。
参考文献:
[1] Marachi N D, Chan C K, Seed H B. Evaluation of properties of rockfill material[J]. Journal of Soil Mechanics and Foundation Division, 1972, 98(1): 95-114.
[2] 花俊杰, 周伟, 常晓林, 等. 堆石体应力变形的尺寸效应研究[J]. 岩石力学与工程学报, 2009, 29(2): 328-335.
HUA Junjie, ZHOU Wei, CHANG Xiaolin, et al. Study of scale effect on stress and deformation of rockfill[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 29(2): 328-335.
[3] 翁厚洋, 朱俊高, 余挺, 等. 粗粒料缩尺效应研究现状与趋势[J]. 河海大学学报, 2009, 37(4): 426-429.
WENG Houyang, ZHU Jungao, YU Ting, et al. Status quo and tendency of studies on scale effects of coarse-grained materials[J]. Journal of Hohai University, 2009, 37(4): 426-429.
[4] 朱俊高, 刘忠, 翁厚洋, 等. 试样尺寸对粗粒土强度及变形试验影响研究[J]. 四川大学学报(工程科学版), 2012, 44(6): 92-96.
ZHU Jungao, LIU Zhong, WENG Houyang, et al. Study on effect of specimen size upon strength and deformation behaviour of coarse-grained soil in triaxial test[J]. Journal of Sichuan University (Engineering Science Edition), 2012, 44(6): 92-96.
[5] 王继庄. 粗粒料的变形特性和缩尺效应[J]. 岩土工程学报, 1994, 16(4): 89-95.
WANG Jizhuang. Studies on deformation properties and scale effects of coarse-grained materials[J].Chinese Journal of Geotechnical Engineering, 1994, 16(4): 89-95.
[6] 阳云华, 赵旻, 关沛强, 等. 膨胀土抗剪强度的尺寸效应研究[J]. 人民长江, 2007, 38(9): 18-22.
YANG Yunhua, ZHAO Min, GUAN Peiqiang, et al. Investigation on size effect of shear strength of expansive soil[J]. Yangtze River, 2007, 38(9): 18-22.
[7] 李翀, 何昌荣, 王琛, 等. 粗粒料大型三轴试验的尺寸效应研究[J]. 岩土力学, 2008, 29(增): 563-566.
LI Chong, HE Changrong, WANG Chen, et al. Study of effect of large-scale triaxial test of oarse-grained materials[J]. Rock and Soil Mechanics, 2008, 29(Supp): 563-566.
[8] 凌华, 殷宗泽, 朱俊高, 等. 堆石料强度的缩尺效应试验研究[J]. 河海大学学报, 2011, 39(5): 540-543.
LING Hua, YIN Zongze, ZHU Jungao, et al. Experimental study of scale effects on strength of rockfill materials[J]. Journal of Hohai University, 2011, 39(5): 540-543.
[9] 朱晟, 王永明, 翁厚洋. 粗粒筑坝材料密实度的缩尺效应研究[J]. 岩石力学与工程学报, 2011, 30(2): 348-357.
ZHU Sheng, WANG Yongming, WENG Houyang. Study of scale effect of density of coarse-grained dam materials[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(2): 348-357.
[10] 史旦达, 周健, 贾敏才, 等. 考虑颗粒破碎的砂土高应力一维压缩特性颗粒流模拟[J]. 岩土工程学报, 2007, 29(5): 736-742.
SHI Danda, ZHOU Jian, JIA Mincai, et al. Numerical simulations of particle breakage property of sand under high pressure 1D compression condition by use of particle flow code[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(5): 736-742.
[11] Potyondya D O, Cundallb P A. Abonded-particle model for rock[J]. International Journal of Rock Mechanics & Mining Sciences, 2004, 41: 1329-1364.
[12] Jiang M J, Yan H B, Zhu H H, et al. Modelling shear behavior and strain localization in cemented sands by two-dimensional distinct element method analyses[J]. Computers and Geotechnics, 2011, 38(1): 14-29.
[13] 李永松, 周国庆, 陈国舟, 等. 颗粒破碎对砂土剪切性质影响的离散单元研究[J]. 土工基础, 2011, 25(6): 53-56.
LI Yongsong, ZHOU Guoqing, CHEN Guozhou, et al. DEM investigations of the influence of particle crushing on the shear properties of sands[J]. Soil Engineering and Foundation, 2011, 25(6): 53-56.
[14] 尹小涛, 郑亚娜, 马双科. 基于颗粒流数值试验的岩土材料内尺度比研究[J]. 岩土力学, 2011, 32(4): 1211-1215.
YIN Xiaotao, ZHENG Yana, MA Shuangke. Study of inner scale ratio of rock and soil material based on numerical tests of particle flow code[J]. Rock and Soil Mechanics, 2011, 32(4): 1211-1215.
[15] Itasca Consulting Group, Inc. PFC (Particle Flow Code), Version 3.1[M]. Minneapolis: ICG, 2005: 2-45.
(编辑 杨幼平)
收稿日期:2014-07-04;修回日期:2014-10-12
基金项目(Foundation item):国家重点基础研究发展规划(973计划)项目(2013CB036404);高等学校博士学科点专项科研基金资助项目(20110094110002);高等学校学科创新引智计划项目(B13024) (Project(2013CB036404) supported by the National Basic Research Development Program of China (973 Program); Project(20110094110002) supported the Specialized Research Fund for the Doctoral Program of High Education; Project(B13024) supported by the Program of Introducing Talents of Discipline for Universities)
通信作者:朱俊高,教授,博士生导师,从事土体本构关系方面的研究;E-mail: zhujungao@163.com