J. Cent. South Univ. (2018) 25: 1154-1164

DOI: https://doi.org/10.1007/s11771-018-3814-8

N-PD cross-coupling synchronization control based on adjacent coupling error analysis

LIU Yan-jie(刘延杰)^{1, 2}, LIANG Le(梁乐)¹, CHU Ting-ting(储婷婷)¹, WU Ming-yue(吴明月)²

1. State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150080, China;

2. HIT-Boshi Research Institute, Harbin Boshi Automation Co., Ltd., Harbin 150078, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: In order to improve the trajectory tracking precision and reduce the synchronization error of a 6-DOF lightweight robot, nonlinear proportion-deviation (N-PD) cross-coupling synchronization control strategy based on adjacent coupling error analysis is presented. The mathematical models of the robot, including kinematic model, dynamic model and spline trajectory planing, are established and verified. Since it is difficult to describe the real-time contour error of the robot for complex trajectory, the adjacent coupling error is analyzed to solve the problem. Combined with nonlinear control and coupling performance of the robot, N-PD cross-coupling synchronization controller is designed and validated by simulation analysis. A servo control experimental system which mainly consists of laser tracking system, the robot mechanical system and EtherCAT based servo control system is constructed. The synchronization error is significantly decreased and the maximum trajectory error is reduced from 0.33 mm to 0.1 mm. The effectiveness of the control algorithm is validated by the experimental results, thus the control strategy can improve the robot’s trajectory tracking precision significantly.

Key words: mathematical model of robot; adjacent coupling error; nonlinear PD control; synchronization control; trajectory tracking accuracy

Cite this article as: LIU Yan-jie, LIANG Le, CHU Ting-ting, WU Ming-yue. N-PD cross-coupling synchronization control based on adjacent coupling error analysis [J]. Journal of Central South University, 2018, 25(5): 1154–1164. DOI: https://doi.org/10.1007/s11771-018-3814-8.

1 Introduction

Compared with traditional industrial robots, the lightweight robot system is a type of robot which offers several advantages such as faster system response, lower energy consumption, better maneuverability and transportability, higher load-to-weight ratio and safer operation owing to reduced inertia. The six-DOF lightweight robots mentioned in this paper, with the total weight just 25 kg and the maximum load 4 kg, are widely used in industrial areas, such as arc welding, assembly and cutting fields with high contour tracking accuracy and high repeatability demands. Since these kinds of lightweight robots are multi-input multi-output and strong nonlinear coupling system, and applied in the complex trajectory conditions which need high real-time capability, it is important to improve the control strategy for the purpose of enhancing the robotic trajectory tracking precision rather than just repeating positioning accuracy.

Amongst most of the conventional controllers, the control loop of each actuator does not receive information from the others. A disturbance in one loop causes an error that is corrected by this loop only, while the others do not respond. However, the structure of the robots brings the difficulties of control as an input to one of the joints will also disturb other joints due to the coupling of the system. The lack of synchronization amongst control loops degrades the motion performance because the trajectory of the end-effector relates to all actuators’ motions.

The cross-coupling synchronization control strategy provides an opportunity to solve the multi- axis control problem with efficient implementation. Coupling rule is difficult to determine when the number of synchronous motors is greater than 2 in the cross-coupling control method, and the control algorithm becomes complex [1]. In recent years, synchronization control technology is widely applied to the multi-axis control system. The cross- coupling control was firstly introduced by KOREN [2] for conventional serial manipulator. FANG [3] presented a cross-coupling controller for tracking contours to effectively reduce the contouring error of a direct-drive robot. PEREZ-PINAL et al [4] proposed the deviation coupling control strategy for synchronous motor with motor number N>2. SUN et al [5] applied the cross-coupling concept in multi-robot coordinated motion control. ALONGE et al [6] applied the synchronization control method to a globally convergent adaptive and robust control of robotic manipulators for trajectory tracking in the presence of friction modelled as static nonlinearities. YANG et al [7] developed a new system to synchronously control the simulated robot and humanoid robot based on the skeletal tracking technology. GAMS et al [8] introduced the synchronization control method to accelerate trajectory adaptation of a dual-arm robot based on learning of coupling terms in the framework of dynamic movement primitives. The cross-coupling synchronization approach has been also found in mobile robots. LIU et al [9] proposed a new synchronous control method via combing high-order sliding mode control techniques with cross-coupling techniques for the attitude control of a novel stair-climbing wheelchair with inertial uncertainties and external disturbance torques.

However, the most of above methods require accurate space contour model to build the mathematical model of synchronization error of the robot, which can make the control algorithm tremendously complex. And the traditional cross-coupling PD control is based on the synchronous control of the motor model, which does not take the inertia coupling effects of robot ontology into the control system. These issues will be overcome in this work. Since the coupling compensation law needs large amount of online calculation while the system contains excessive number of motors, hard-real-time and high- performance communication bus are in greater demand. Real-time EtherCAT can achieve high performance of anti-interface and robustness in process, especially for high-speed, high-reliability, high-real-time data transfer applications [10]. GUO et al [11] introduced the EtherCAT fieldbus for the control system of quadruped robot. CHOI et al [12] used EtherCAT in multi-robot system.

In this work, a synchronized control strategy based on adjacent coupling error analysis is proposed, by incorporating cross-coupling technology into a nonlinear PD control architecture. To improve the comprehensive performance of the multi-axis robot system, the proposed control method is used to not only improve the single-axis control, but also coordinate the motion control of each axis, so that the robot can achieve satisfactory motion precision as well as good synchronization performance. Compared to many existing synchronization approaches, the proposed method is easy to implement with simple calculation. Experiments conducted on a 6-DOF lightweight serial robot system under the EtherCAT protocol demonstrate that the proposed approach can improve the trajectory tracking precision effectively. Besides, the algorithm can be also applied to other multi-joint serial robots which have requirements of trajectory tracking accuracy.

2 Mathematical model of 6-DOF lightweight robot

2.1 Kinematic model

The mechanical body of IRB120 robot and a reconstructive control system are used as experimental platform for verification of the control algorithm. The robot which has six rotational degrees of freedom is composed of the base, waist, upper arm, forearm and wrist as show in Figure 1.

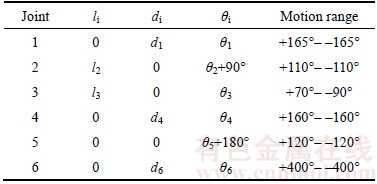
Figure 2 shows the D-H coordinate system of the robot mechanism and Table 1 presents the main structural parameters of the robot. Kinematic calibration method was used to identify the real values of the kinematic parameters and correct the robot kinematic model to improve the robot accuracy [13].

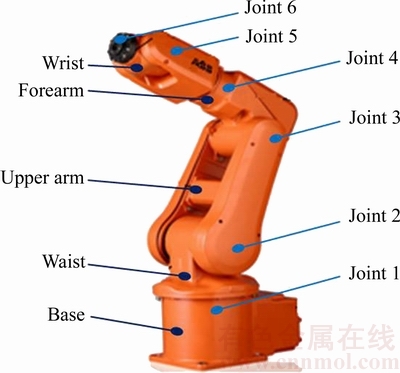
Figure 1 Mechanical body of IRB120 robot

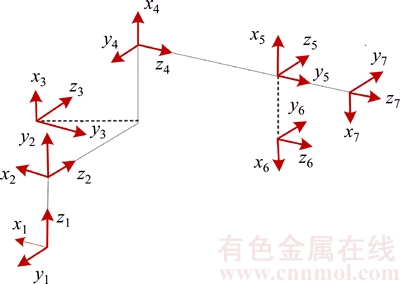
Figure 2 D-H coordinate system of robot mechanism

Table 1 Main structural parameters of robot

According to the geometrical characteristics of the robot, the forward kinematics model can be got using D-H method:

(1)

where p_x, p_y, p_z denote the position coordinates of the end-effector; l_i is the length of robot link; d_i is the offset distance; θ_i is the joint angle; cθ_i is short for cosθ_i; sθ_i is short for sinθ_i; θ_ij is short for θ_i+θ_j.

The counter transformation method is used to solve the inverse kinematics model of the robot.

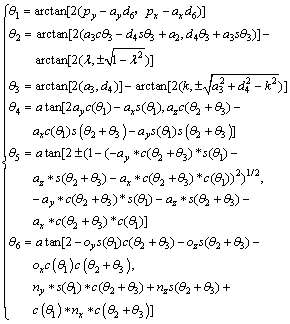(2)

Since there are eight inverse kinematic solutions, the weight optimization function is used to select the optimal solution.

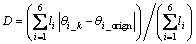            (3)

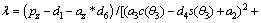
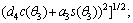
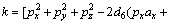
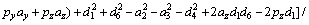
where θ_{i_k} is the ith joint calculated value of the kth group solutions; θ_{i_orign} is the ith joint calculated value before the current moment.

In order to verify the correctness of the kinematic model, the comparison between forward and inverse kinematic solutions is shown in Figure 3.

The blue circles are coordinate values of the robot end-effector along different routes, which is calculated by the forward kinematic model. Using these values, joint space coordinates can be got by the inverse kinematic model. Then recalculated by the forward kinematic model, the position of the end-effector can be got again, which is marked by the red circles. The comparison results show that the position error is less than 10×10^–14 which can verify the accuracy of the kinematic model.

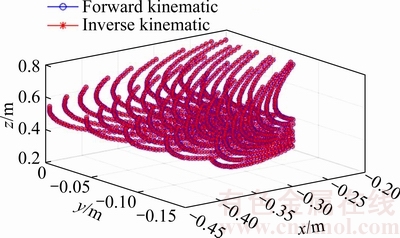
Figure 3 Comparison between forward and inverse kinematic solutions

2.2 Dynamic model

The kinetic energy of all components can be calculated and the dynamics equation can be obtained using the second type Lagrange equation [1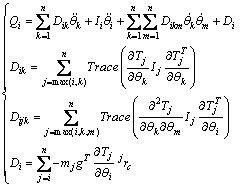4]:

      (4)

where I_i is the rotational inertia of the ith transmission mechanism; T_j is the transformation matrix.

The dynamic model of the robot can be edited as follows:

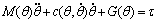                  (5)

where M(θ) is the inertia matrix; 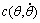is coriolis force item and centrifugal force item; G(θ) is gravity item.

The virtual prototype model can be obtained using Adams and Simulink. The output-torque error between dynamic model and simulation model is shown in Figure 4. It can be observed that the error of joint 1 to joint 3 is less than 0.1 N·m, and the error of joint 4 to joint 6 is less than 0.004 N·m, which can verify the correctness of the dynamic model.

2.3 Spline trajectory planning

For any spline curves, high-order polynomial interpolation can be used to obtain accurate interpolation trajectory. The quintic polynomial interpolation form which can make position curves, velocity curves and acceleration curves smooth is shown as follows:

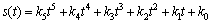          (6)

where k_i (i=0, …, 5) are interpolation coefficients.

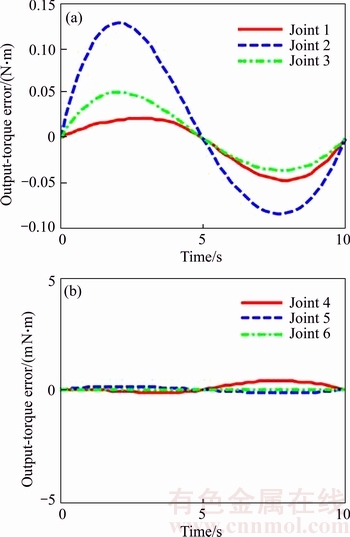
Figure 4 Output-torque error between dynamic model and simulation model

The initial states of the robot are set as: starting position s₀, starting velocity v₀, starting acceleration a₀, ending position s_f, ending velocity v_f, ending acceleration a_f and running time t_f. Based on the above initial values, Eq. (6) can be calculated as follows:

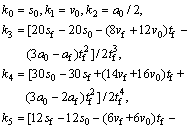
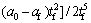                       (7)

Figure 5 shows the trajectory planning results using quantic spline curves, when the robot walk from A (–0.230, 0, 603) to B (0, 0.304, 0.556).

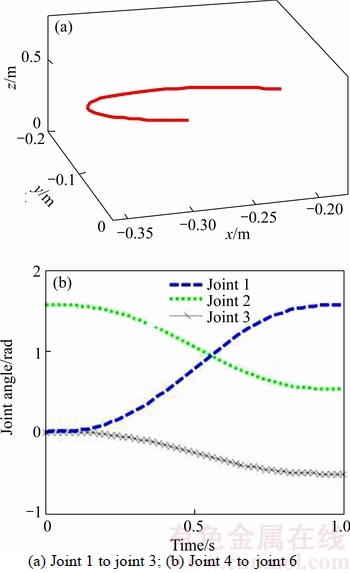
Figure 5 Spline trajectory planning results

3 Design of synchronization controller

3.1 Adjacent coupling error analysis

For a multi-axis motion control system, the contouring errors intensely affect the quality of the machined workpieces [15], and the robot task trajectory is usually complex such as arc welding process. So, it is difficult to establish proper coupling rules and there will be huge amount of calculation on-line using the existing algorithms. Aiming at these problems, a synchronized control idea in 6-DOF robot systems with the minimum number of correlative axe was produced [16].

The objectives for synchronous control system of the 6-DOF robot [17, 18] are:

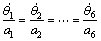                         (8)

where a_i is the synchronization proportional coefficient.

The tracking speed error is the difference between desired velocity of the ith joint 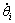and real velocity which is as follows:

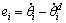                              (9)

In order to obtain the proper synchronization motion, e_i→0 is required along with:

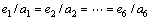                 (10)

ζ_i is the synchronous speed error of joint i which can be calculated as follows:

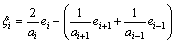              (11)

The goal of synchronous control is to make ζ_i=0.

Substituting ζ_i into Eq. (12) obtains the adjacent coupling error E_i, which not only considers the tracking speed error about the ith joint but also its adjacent joints.

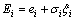                            (12)

where σ_i is a positive coupled error coefficient. And the larger the σ_i is, the bigger the weight of the synchronous speed error will be [19].

3.2 N-PD cross-coupling synchronization controller

In order to improve the trajectory tracking precision of the 6-DOF robot, a method of nonlinear proportion-deviation (N-PD) cross- coupling synchronization control strategy based on adjacent coupling error is proposed in this work.

The hyperbolic cosine function is introduced as the nonlinear gain of the controller:

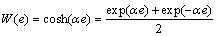         (13)

where α is the error scaling factor; e is control system error. W(e) tends to 1 when e tends to 0, and as e increases, W(e) also increases.

The separate function is designed to prevent W(e) from increasing infinitely:

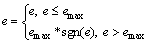                  (14)

The simulation results of step response are shown in Figure 5, where α, e_max, K_p, K_d are set to 0.105, 6, 5 and 0.415 respectively. It is observed that the transition time of nonlinear PD control system (0.55 s) is much shorter than linear PD system (0.95 s), which can confirm nonlinear PD control algorithm can significantly improve the response speed of the robot.

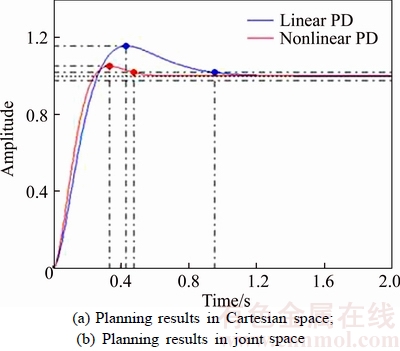
Figure 6 Step response comparison between linear PD and nonlinear PD control system

The N-PD cross-coupling synchronization control strategy which possesses speed and acceleration feedforward items simultaneously is shown as follows:

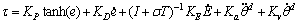(15)

where K_P, K_D, K_E, K_a and K_v are diagonal positive definite gain matrixes; 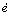and 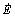are tracking speed error rate and adjacent coupling error rate respectively.

Combining with Eq. (5), the control system can be obtained as follows:

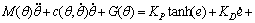
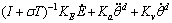           (16)

The control block diagram of the first three- joint servo systems is shown in Figure 7.

In order to prove the stability of the control method, Lyapunov function was designed as follows:

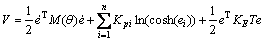  (17)

where K_pi is the ith diagonal element of K_p, and K_E is diagonal positive definite gain matrix which meets the requirement of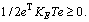

Since the bounded inertia matrix M(θ) is symmetric positive definite 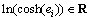and and 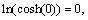V is a positive definite function. The derivative of function V is as follows:

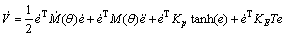(18)

Combining Eq. (16) and antisymmetric matrix 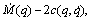it can obtain:

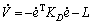                          (19)

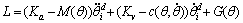
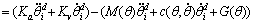  (20)

It can be seen that through adjusting the diagonal positive definite gain matrixes K_a and K_v to make L≥0, the control system can be globally asymptotically stable, which is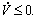

4 Simulation analysis

To verify the effectiveness of the algorithm, the robot will be run along the planned spline trajectory. The comparison between the actual trajectory and desired trajectory of the robot under different control methods is shown in Figure 8, which is compared with the trajectory deviation of the end-effector along different directions respectively. And the trajectory deviation ranges in the x, y, z directions are shown in Table 2.

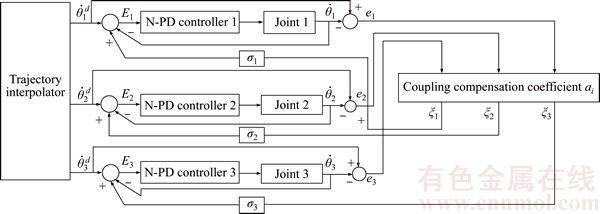
Figure 7 Control block diagram of first three joint servo systems

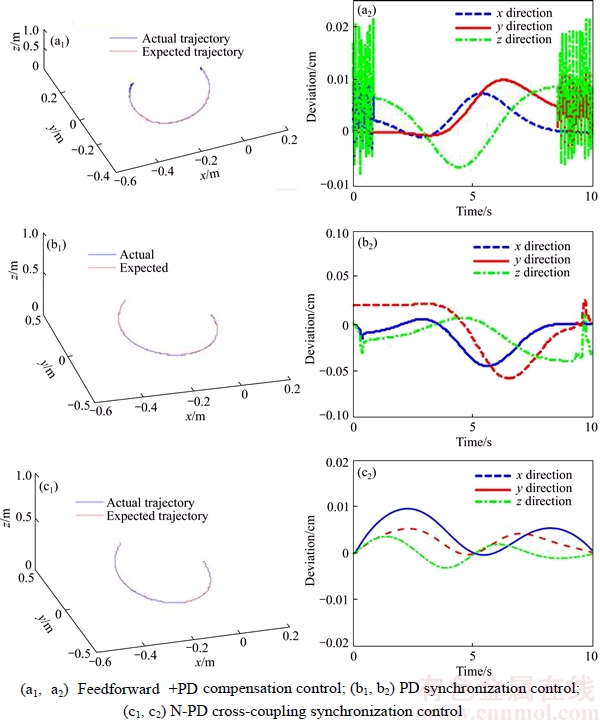
Figure 8 Trajectory tracking ability of robot under three different control methods

Table 2 Trajectory deviation range of robot

It can be observed from Figure 8 and Table 2, using N-PD cross-coupling synchronization control method, the trajectory deviation of the robot is less than 0.1mm in three directions, which can realize complex curve precision tracking compared with others.

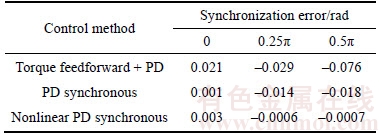
Taking joint 1 as an example, Figure 9 shows the displacement and the synchronization error of joint 1 using the three methods. Table 3 shows the values of synchronization error in different locations.

According to the simulation results in Figure 9 and Table 3, the synchronization error of joint 1 is gradually decreasing in accordance with the order of torque feedforward + PD, PD synchronous and N-PD cross-coupling synchronization control methods. Accompanied the introduction of saturated nonlinear function tanh(·), the synchronization performance is greatly enhanced and the maximum synchronization error is less than 0.001rad.

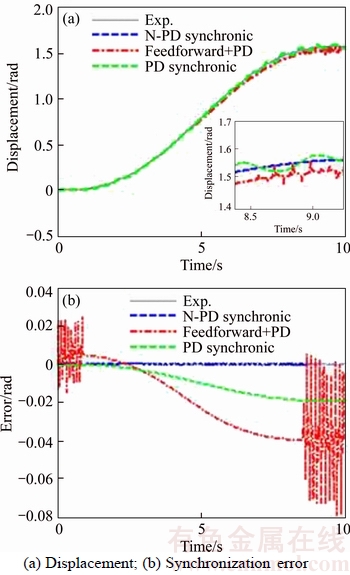
Figure 9 Tracking performance of joint 1 under three different methods

Table 3 Synchronization error of joint 1

5 Experimental verification

5.1 Experimental system

A servo control system based on EtherCAT bus and 6-DOF lightweight robot body experimental platform was built in this work. Figure 10 shows the entire experimental system which mainly consists of three components: laser tracking system, servo control system and the robot mechanical system.

Beckhoff IPC was used as industrial computer which included TwinCAT3 programming software. The ADSA servo drives were applied in this work which supported EtherCAT bus communications. So real-time communication and motor control could be realized via high-speed EtherCAT bus.

5.2 Experimental verification

In order to improve the trajectory accuracy of the robot, the N-PD cross-coupling synchronization control strategy based on speed dual-loop control system was designed [20].

The moving trajectory of the robot was configured along the spline curve as previously mentioned, and the running time was set to 5000ms. The velocity of each joint was calculated by Jacobi matrix, and the adjacent coupling error model was compensated into the torque loop by PD controller. The comparisons of synchronization error and trajectory error between traditional PD synchronization control and N-PD cross-coupling synchronization control are shown in Figures 11 and 12, respectively.

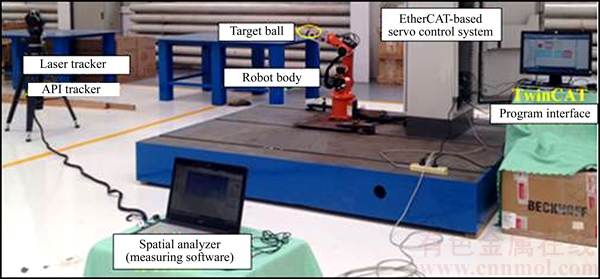
Figure 10 Experimental system

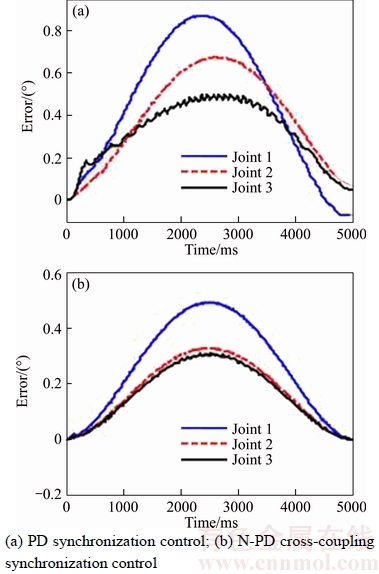
Figure 11 Synchronization errors of first three joints

It can be seen in Figure 11, the synchronization error ranges of joint 1, joint 2 and joint 3 under the traditional PD synchronization control method are (–0.08°–0.883°), (0.03°–0.651°) and (0°–0.443°) respectively. And the error ranges under the N-PD cross-coupling synchronization control method adding the nonlinear saturation function tanh(·) are (0°–0.456°), (0°–0.327°) and (0°–0.311°) respectively. The synchronization errors of joint 1 and joint 2 are significantly reduced, and the error curve of joint 3 becomes smoother obviously.

According to Figure 12, the trajectory error curve of the robot becomes smoother and the maximum error is reduced from 0.33mm to 0.1mm, when using N-PD cross-coupling synchronization control algorithm instead of traditional PD synchronization control algorithm. The effectiveness of the control algorithm is validated by the experimental results, thus the control strategy can improve the robot’s trajectory tracking precision significantly.

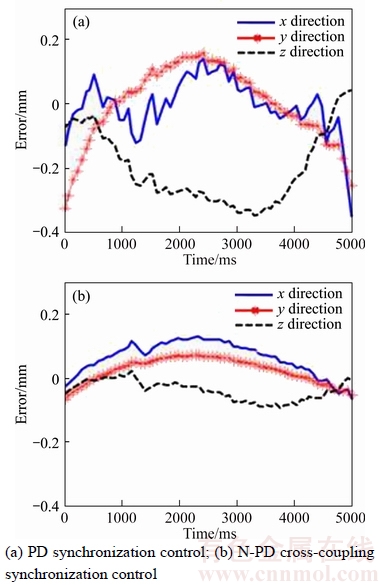
Figure 12 Trajectory error of robot

6 Conclusions

1) The mathematical model of the 6-DOF lightweight robot is deduced and verified by virtual prototype model and mathematical tools, which can be used for robot controller design and trajectory planning.

2) A control strategy based on adjacent coupling error analysis is proposed, which has considered nonlinear control and coupling performance of the robot. And the stability of the control method is validated by Lyapunov function.

3) The trajectory tracking ability of the robot under three different control methods is compared through simulation. The simulation results show that the control strategy can realize complex curve precision tracking.

4) The experimental system is set up, which consists of laser tracking system, the robot mechanical system and servo control system. The synchronization error is significantly decreased and the maximum trajectory error is reduced from 0.33mm to 0.1mm.

5) The future work is about the establishment of an improved closed loop control system of the robot, which increases sensors and considers the influence of the load and external disturbance.

References

[1] CHENG H M, MITRA A, CHEN Cheng-yi. Synchronization controller synthesis of multi-axis motion system [C]// International Conference on Innovative Computing. 2009: 918–921.

[2] KOREN Y. Cross-coupled biaxial computer controls for manufacturing systems [J]. Journal of Dynamic Systems Measurement & Control, 1980, 102(4): 265–272.

[3] FANG Ren-wu, CHEN Jian-shiang. Cross-coupling control for a direct-drive robot [J]. JSME International Journal, 2002, 45(3): 749–757.

[4] PEREZ-PINAL F J, NUNEZ C, ALVAREZ R. Comparison of multi-motor synchronization techniques [C]// Industrial Electronics Society, Conference of IEEE. 2004(2): 1670–1675.

[5] SUN D, MILLS J K. Adaptive synchronized control for coordination of multirobot assembly tasks [J]. IEEE Transactions on Robotics & Automation, 2002, 18(4): 498–510.

[6] ALONGE F, D'IPPOLITO F, RAIMONDI F M. Globally convergent adaptive and robust control of robotic manipulators for trajectory tracking [J]. Control Engineering Practice, 2004, 12(9): 1091–1100.

[7] YANG Ning-jia, DUAN Feng, WEI Yu-di, LIU Chuang, TAN T C, XU Bin-bin, ZHANG Jin. A study of the human-robot synchronous control system based on skeletal tracking technology [C]// IEEE International Conference on Robotics and Biomimetics. 2013: 2191–2196.

[8] GAMS A, UDE A, MORIMOTO J. Accelerating synchronization of movement primitives: Dual-arm discrete- periodic motion of a humanoid robot [C]// IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2015.

[9] LIU Juan-xiu, WU Yi-fei, GUO Jian, CHEN Qing-wei. High-order sliding mode-based synchronous control of a novel stair-climbing wheelchair robot [J]. Journal of Control Science & Engineering, 2015, 2015(46): 1–16.

[10] GU Kai, CAO Qi-xin. Control system design of 6-DOFs serial manipulator based on real-time Ethernet [C]// IEEE International Conference on Information and Automation. 2014: 118–120.

[11] GUO Kun, LI Shao-yuan, HUANG D. Real-time quadruped robot control system based on Xenomai [C]// Chinese Automation Congress. IEEE, 2015: 342–347.

[12] CHOI T, DO H, PARK D, PARK C, KYUNG J. Real-time synchronisation method in multi-robot system [J]. Electronics Letters, 2014, 50(24): 1824–1826.

[13] LI Tian, SUN Kui, XIE Zong-wu, LIU Hong. Optimal measurement configurations for kinematic calibration of six-DOF serial robot [J]. Journal of Central South University of Technology, 2011, 18(3): 618–626.

[14] YOU Wei, KONG Min-xiu, SUN Li-ning, DU Zhi-jiang. Optimal design of dynamic and control performance for planar manipulator [J]. Journal of Central South University, 2012, 19(1): 108–116.

[15] ZHANG Dai-lin, ZHANG Xu, XIE Jing-ming, YUAN Chu-ming, CHEN You-ping, TANG Yang-ping. Contouring error modeling and simulation of a four-axis motion control system [J]. Journal of Central South University, 2015, 22(1): 141–149.

[16] SUN D, TONG M C. A synchronization approach for the minimization of contouring errors of CNC machine tools [J]. IEEE Transactions on Automation Science & Engineering, 2009, 6(4): 720–729.

[17] LIU H H T, SUN D. Uniform synchronization in multi-axis motion control [C]// American Control Conference, 2005, Proceedings of the 2005. IEEE, 2005: 4537–4542.

[18] SUN D, SHAO Xiao-shao, FENG Geng. A model-free cross-coupled control for position synchronization of multi-axis motions: Theory and experiments [J]. IEEE Transactions on Control Systems Technology, 2005, 38(1): 1–6.

[19] CROSS M C, ROGERS J L, LIFSHITZ R, ZUMDIECK A. Synchronization by reactive coupling and nonlinear frequency pulling [J]. Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2006, 73(2): 80–98.

[20] DENG W, LOW K S. Cross-coupled contouring control of a rotary based biaxial motion system [C]// International Conference on Control, Automation, Robotics and Vision. IEEE, 2006: 1–6.

(Edited by YANG Hua)

中文导读

一种基于相邻耦合误差分析的非线性PD偏差耦合同步控制方法

摘要：为了提高六自由度轻量型机器人的轨迹跟踪精度同时减小其同步误差，提出一种基于相邻耦合误差分析的非线性PD偏差耦合同步控制方法。建立并验证了该机器人的数学模型，包括运动学模型、动力学模型以及样条轨迹规划。因为难以描述复杂轨迹下的机器人实时轮廓误差，因此本文引入相邻耦合误差来解决这一问题。结合机器人非线性控制以及耦合特性，设计了非线性PD偏差耦合同步控制器，并通过仿真分析进行验证。伺服控制试验系统由激光跟踪系统、机器人机械系统以及基于EtherCAT通讯的伺服控制系统构成，实验数据表明，该控制方法可使机器人同步误差大幅度减小，并且最大跟踪误差由0.33 mm缩减到0.1 mm。实验结果验证了控制算法的有效性，从而证明了该控制策略能够有效改善机器人的轨迹跟踪精度。

关键词：机器人数学模型；相邻耦合误差；非线性PD控制；同步控制；轨迹跟踪精度

Foundation item: Project(2015AA043003) supported by National High-technology Research and Development Program of China; Project(GY2016ZB0068) supported by Application Technology Research and Development Program of Heilongjiang Province, China; Project(SKLR201301A03) supported by Self-planned Task of State Key Laboratory of Robotics and System (Harbin Institute of Technology), China

Received date: 2016-09-22; Accepted date: 2016-12-08

Corresponding author: LIU Yan-jie, PhD, Professor; Tel: +86-451-86403709; E-mail: yjliu@hit.edu.cn; ORCID: 0000-0002-7274-4979