J. Cent. South Univ. (2017) 24: 1155-1163

DOI: 10.1007/s11771-017-3518-5

Assessment of bearing performance degradation via extension and EEMD combined approach

LIU Yu-mei(刘玉梅)¹, ZHAO Cong-cong(赵聪聪)², XIONG Ming-ye(熊明烨)³, ZHAO Ying-hui(赵颖慧)⁴,

QIAO Ning-guo(乔宁国)¹, TIAN Guang-dong(田广东)¹

1. Transportation College, Jilin University, Changchun 130022, China;

2. College of Engineering and Technology, Jilin Agricultural University, Changchun 130118, China;

3. University of Illinois at Urbana-Champaign, Illinois, Champaign-Urbana 61801, USA;

4. Engineering Department, Changchun Visteon Faway Automotive Electronics Co., Ltd., Changchun 130011, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2017

Abstract: As a key component in rotating machinery, the operating reliability of bearing influences the performance and service life of the equipment directly. In order to describe bearing performance degradation (BPD) process effectively, an assessment approach combining extension and ensemble empirical mode decomposition (EEMD) was proposed. First, the extension was utilized to construct the matter-element of bearing operating state, and the energy moment of intrinsic mode functions (IMFs) was used as characteristic parameter of the matter-element. Then, to determine classical domains of characteristic parameters, the mathematical statistics method was adopted. Finally, the BPD was analyzed qualitatively and quantitatively according to the comprehensive correlation degree of bearing current operating state related to its healthy state. The analytic results of bearing test-rig show that the proposed method indicates the incipient fault approximately occurring in the 81st hour, and the method also quantitatively presents the degree of BPD. By contrast, the BPD assessment based on time-domain features extraction method could not achieve the above two results effectively.

Key words: bearing; performance degradation assessment; extension; ensemble empirical mode decomposition; mathematical statistics

1 Introduction

Due to the important role of bearing in rotating machinery, it results in dramatically deterioration of machine operating condition and causes catastrophic accident once a bearing goes terribly wrong [1, 2]. In addition, fault prognostic of bearing is of great significance to identify future conditions for maintenance plans, which also benefits to reduce production downtime and maintenance cost [3]. However, effective bearing performance degradation (BPD) assessment is still a challenge in academia and industries. The main problems are feature extraction and pattern identification. On one hand, extracting feature vector of bearing vibration signal (BVS) effectively is the precondition for bearing fault diagnosis. On the other hand, fast-accurate state identification method is an important way to realize bearing fault diagnosis.

Because of the complexity of bearing working condition, its vibration signal is easily affected by non-stationary factors [4], which will cause non-linear and non-stationary features of BVS. As a new time-frequency analysis method, empirical mode decomposition (EMD) could process non-linear and non-stationary signal, but one of its major drawbacks is mode mixing [5]. WU et al [6] and ZHANG et al [7] presented an improved version of EMD, called ensemble EMD (EEMD), which overcomes the mode mixing problem caused by EMD effectively. Many researchers have used EEMD as a signal processing tool and also extracted fault features based on intrinsic mode functions (IMFs) decomposed by EEMD. LEI et al [8] proposed an EEMD-based method for fault diagnosis of rotating machinery and obtained a more precise diagnosis result for the fault location. OZGONENEL et al [9] studied EEMD performance and compared it with classical EMD in feature vector extraction.

Over the past years, BPD analysis has attracted much research attention and many intelligent diagnostic technologies, e.g., support vector machine [10], artificial neural network (ANN) [11], Gaussian mixture model (GMM) [12], and hidden markov model [13, 14], which have been adopted to bearing operating state monitoring and fault diagnosis. For example, YU et al [12] utilized GMM to diagnose bearing fault and estimate the severity of fault. HUANG et al [15] proposed a self-organize-map and ANN-based method for bearing performance degradation assessment.

Unfortunately, current BPD assessment methods mainly focus on fault feature extraction and fault identification, the study about detecting incipient fault is relatively few. Instead, extension, established and developed by CAI et al [16, 17] in 1983, provides a qualitative and quantitative method for incompatibilities and conflicts. With the deep study of extension, it has been successfully applied to engineering [18, 19], environment [20] and economy [21] fields, etc. The outstanding advantage of extension is that it quantifies the qualitative indices, which makes the evaluation results more precise and profound. Therefore, it is essential to utilize extension in BPD assessment to detect incipient fault as well as assess BPD quantitatively.

In this work, an assessment method of BPD combined extension and EEMD was proposed and demonstrated.

2 Matter-element model for bearing operating state

In fact, bearing goes through a series of degrading states before failure eventually occurs. To describe bearing operating state, the matter-element is constructed firstly. Then the statistical method is adopted to determine the two most important sets in extension.

2.1 Basic concepts in extension

2.1.1 Matter-element

Matter-element is the logic cell of extension [16, 17]. Object O has a characteristic c and its value is v, then matter-element could be expressed as R=(O, C, v). If object O has n characteristics, then it will be described by a n-dimensional matter-element.

2.1.2 Correlation function

Let X₀=1, x₂>, X=3, x₄>, X₀∈X, X₀ and X have no public endpoints, the correlation function is expressed as follows [18-21]:

            (1)

   (2)

   (3)

where X₀ and X are classical and segment domains, respectively. K(x) is the correlation degree of x related to X₀. The sign and value of K(x) present the degree that x belongs to X₀ or not.

2.2 Matter-element model for bearing operating state

An n-dimensional matter-element R which presents bearing operating state could be expressed as below via selecting suitable characteristics:

                   (4)

where O represents the bearing operating state to be assessed. C=[c₁, c₂, …, c_n] is the eigenvector, and V=[v₁, v₂, …, v_n] is the value of C. As bearing operating state is described by different parameters, thus the first column of n-dimensional matter-element only use O to present bearing operating state. The n-dimensional matter- element presenting bearing operating state below could be explained by the same way.

Classical matter-element of bearing operating state could be presented as follows:

                   (5)

where O_c represents bearing healthy operating state. V_ci = ci, b_ci> is the classical domain of the i-th characteristic parameter. a_ci and b_ci are the lower and upper limit of V_ci , respectively.

Segment matter-element of bearing operating state is presented as follows:

                  (6)

where O_p represents all bearing operating states, including the states from health to failure. V_pi =pi, b_pi> is the segment domain of the i-th characteristic parameter. a_pi and b_pi are the lower and upper limit of V_pi, respectively.

According to Eqs. (1)-(6), CCD which represents bearing current operating state related to its healthy state, could be defined as

                           (7)

where ω_i is the weight coefficient of the i-th characteristic parameter. K(v_i) is the correlation degree of the i-th characteristic parameter value v_i related to its classical domain V_ci.

The degree of BPD could be expressed qualitatively and quantitatively according to the sign and value of K(O). If K(O)>0, bearing is in its healthy operating state; if K(O)=0, bearing’s healthy state will change into failure state; if K(O)<0, the fault occurs and bearing would be in its failure state. In addition, the value of K(O) indicates the degree of health or failure.

2.3 Determination of classical and segment domains

Classical and segment domains are typical extension sets. Accurately defining the two sets is the precondition for fault diagnosis and state monitoring. Let the mean and variance of random variable Z be EZ and σ², respectively, then Chebyshev inequality is expressed as below:

                       (8)

Let confidence level be 95%, then we will get ε= 4.47σ. That is to say P(EZ-4.47σi-4.47σ_i, EZ_i+4.47σ_i] could be regarded as the classical domain of the i-th characteristic parameter in matter-element, where EZ_i and σ_i are the mean and variance of the i-th characteristic parameter, respectively.

Segment domain is a set of all classical domains. It could be determined according to the properties or classical domains of characteristic parameters.

3 Feature extraction based on EEMD

As stated in the previous section, a suitable vibration signal processing method is needed to obtain feature vector which describes bearing operating state accurately. In this section, a feature extraction method based on EEMD is illustrated in detail.

3.1 EEMD

Though EMD is applicable to non-linear and non-stationary signals, it has a problem of mode mixing. While EEMD method, presented by WU et al [6] on the basis of researching the EMD results of white noise, could overcome this mode mixing problem. EEMD is a noise-assisted data analysis method. The process of EEMD could be summarized as follows [5].

Step 1: Initialize the number of ensemble H, the amplitude of the added white noise q, and h=1.

Step 2: Add a white noise series s_i(t) with finite amplitude to the original signal y(t):

                            (9)

where y_i(t) represents a noise-added signal of the i-th trial.

Step 3: Decompose each noise-added signal y_i(t) with EMD into IMFs l_ij(t) and the residue r_i(t):

                         (10)

where l_ij(t) is the j-th IMF of the i-th trial, j=1, 2, …, J. J is the number of IMFs, r_i(t) is the residue of the i-th trial.

Step 4: If h

Step 5: Calculate the ensemble means l_j(t) of H trials for each IMF of the decomposition as the final result:

              (11)

where l_j(t) (j=1, …, J) is the j-th IMF components with EEMD method and r(t) is the residue of H trials with EEMD.

Under ideal condition, each IMF is a simple stationary signal and presents one feature components of the original signal. However, false components inevitably exist in EEMD decomposition results. Thus, the IMFs which could better reflect the properties of the original signal are chosen according to the correlation coefficients (CCs) of IMFs related to the original signal. CC is expressed as below:

   (12)

where l_j(t) (j=1, …, J) is the j-th IMF components, X is the original signal, and N is the number of data points.

3.2 Feature extraction

Feature extraction is the foundation for constructing the matter-element of bearing operating state. Since the energy contained in IMFs is different from each other, and the energy moment is related to the signal amplitude as well as to the changing trend of energy over time [22], thus the energy moments of IMFs are used as characteristic parameters to construct the matter-element of bearing operating state.

The extraction process of energy moment of IMF is presented as below:

1) Decompose signal y(t) into m-IMF(l_i(t)) with EEMD.

2) Calculate the energy moment of the i-th IMF:

                            (13)

The discrete data’s energy moment is:

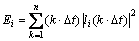                     (14)

where Δt is sampling period, n is the total sample point and k is sample point.

3) Normalize the eigenvector of energy moment.

The total energy is

                                 (15)

Then the normalized eigenvector is

                     (16)

E is the eigenvector in the matter-element of bearing operating state.

4 Process of proposed method in BPD assessment

This work proposes a BPD assessment method integrating extension and EEMD. The detailed steps are presented as follows and its flowchart is shown in Fig. 1.

1) Decompose BVS into m IMFs with EEMD;

2) Calculate CC of each IMF related to the original signal and select IMFs which could better reflect the properties of the original signal;

3) Calculate the normalized eigenvector of IMFs’ energy moments according to Eqs. (13)-(16);

4) Establish the matter-element presenting bearing current operating state;

5) Determine the classical and segment domains of characteristic parameters;

6) Calculate CCD according to Eq. (7), then assess BPD quantitatively and qualitatively based on the sign and value of CCD.

5 Experimental analysis

In order to verify the effectiveness and feasibility of the proposed method for BPD assessment, a bearing run-to-failure test is taken to describe this assessment process in detail. The experimental data used in this work is from Ref. [23] and the test rig is shown in Fig. 2. Four bearings are installed on one shaft which is driven by an AC motor and coupled by rub belts. The angular velocity is kept at 2000 r/min constantly. A 22672 N radial load is applied onto the shaft and bearings by a spring mechanism. Two accelerometers (vertical-Y direction and horizontal-X direction) are installed on each bearing. Sampling rate is fixed at 20 kHz. This run-to-failure test lasts about 164 h, and the vibration signal is collected every 10 min. After the experiment, bearing 1 has an outer-race fault.

This work takes bearing 1 as the researching object and analyzes its vertical vibration acceleration signal. To get the IMFs which could better reflect the properties of the original signal, ten groups of data are taken from the initial stage of the run-to-failure trial, the data length of each group is 2048 points.

Figure 3 shows a group of the original vibration signal. The ordinate presents the ratio of bearing vibration acceleration tested to the acceleration of gravity(g). Performing EEMD and EMD on the signal, the decomposition results are shown in Fig. 4. The parameters used to run EEMD algorithm are 100 trial number and 0.2 time of the standard deviation of the contaminated signal, respectively. From Fig. 4, it could be seen that the signal is decomposed into 10 IMFs and one residual signal. By comparison, mode mixing occurs from IMF2 to IMF6 with EMD method. Instead, EEMD overcomes this problem.

According to Eq. (12), calculating CCs of IMFs and residual signal related to theirs’ original signals, the result is shown in Figs. 5 and 6. The average of CCs is presented in Table 1. The mean values of the first eight

CCs are greater than 0.1 and those of the rest are less than 0.1. It could be regarded that the first eight IMFs better reflect the properties of the original signal. Thus, the energy moments of the first eight IMFs are extracted as the eigenvector to construct the matter-element of bearing operating state.

Fig. 1 Flowchart of evaluation process for BP

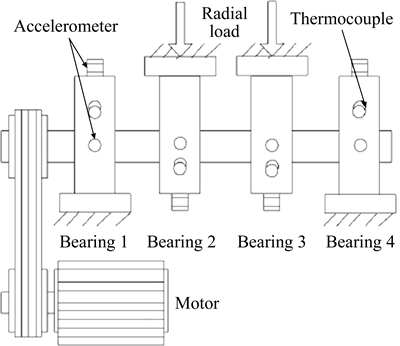
Fig. 2 Bearing test rig

Fig. 3 Original vibration signal

Since the bearing run-to-failure test lasts 164 h, it could be considered that bearing is in its healthy state at the beginning of the test. To determine classical domains, the energy moments of IMFs of the first 25 h data files are calculated. The specific processes of determination of classical domains are listed as follows:

1) Collect vibration signals every 30 min and get 50 groups of data in total. The data length of each group is 2048 points;

2) Perform EEMD on the data groups and calculate the normalized energy moment eigenvector according to Eqs. (13)-(16).

3) Calculate the average value and standard deviation of the normalized energy moment, then determine the classical domains according to Eq. (8).

The results of classical domains are shown in Table 2.

The classical matter-element could be constructed as

               (17)

Due to the normalization feature of the energy moment eigenvector, the interval of each energy moment of IMF is [0,1], which means the segment of each index is [0,1]. Thus, the segment matter-element of bearing operating state could be constructed as below:

                     (18)

In Eqs. (17) and (18), c_i (i =1, 2, …, 8) is the energy moment of the i-th IMF.

To indicate the assessment process of BPD, the matter-element of bearing operating state should be established first. The vibration signal is collected every hour, and then the matter-element is constructed according to the feature extraction method mentioned above. Let the weight coefficient of each characteristic parameter be equal, that is the weight coefficient of the i-th index is 0.125. Then according to Eq. (7), we could get the curve of CCD over time, as shown in Fig. 7.

According to Fig. 7, the BPD process could be divided into four states:

State 1 is from the beginning of the test to 81 h. During this state, the sign of CCD is positive and the variation of CCD amplitude is not significant, which presents that bearing is in its perfect state without degradation occurring.

State 2 is from 81 to 102 h. During this state, the sign of CCD is still positive yet its value declines apparently, which presents that bearing is gradually deviating from its perfect state, early fatigue wear begins to appear but bearing is still functional.

State 3 is from 102 to 160 h. During this state, the sign of CCD is negative and its value decreases continuously which presents that the performance of bearing is continuously deteriorating.

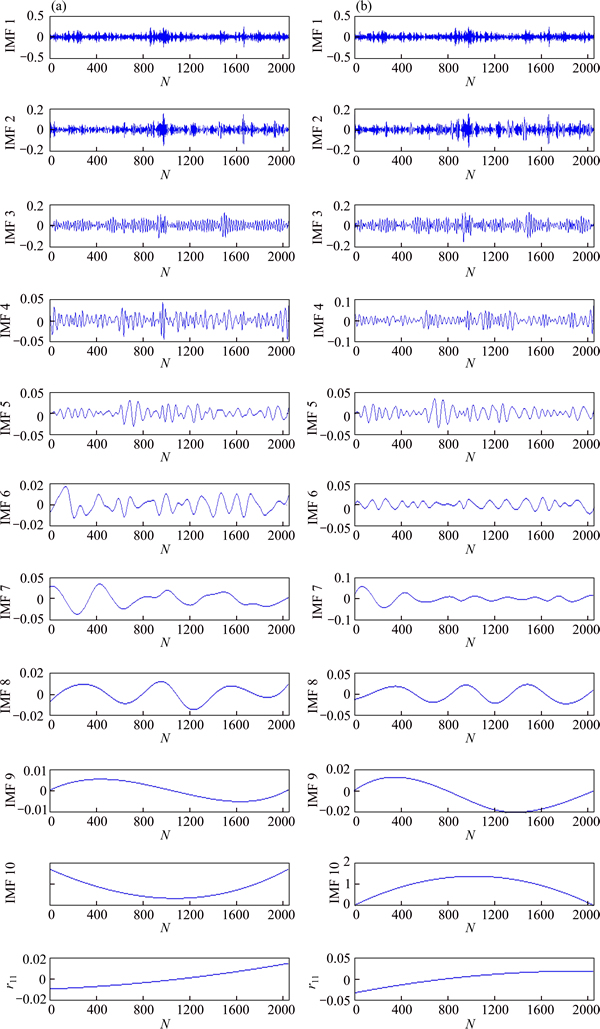
Fig. 4 Decomposition result with EEMD (a) and EMD (b)

Fig. 5 CC of IMF related to original signal

Fig. 6 Average value of CC

Table 1 Average value of CC

Table 2 Classical domains of characteristic parameters

State 4 is from 161 h to the end of the test. During this state, the value of CCD declines dramatically which means that bearing falls in its severe fault stage.

To verify the effectiveness of the proposed method in assessment of BPD and detection of incipient fault, the time-domain feature extraction-based method is adopted as a comparison analysis in this work. The expressions of the time-domain indices are listed in Table 3 and the curves of these indices over time are shown in Fig. 8.

Fig. 7 Curve of CCD over time

Table 3 Expression of time-domain indices

As shown in Fig. 8, the process of BPD could be divided into two or three states. If the crest factor is adopted as the index, the process is divided into two states. Otherwise, the process is divided into three states and described as follows:

State 1 is from the beginning of the test to 102.3 h. During this state, the variation in amplitude is not obvious and bearing works normally. This state is corresponding to state 1 and state 2 in Fig. 7.

State 2 is from 102.3 to 160 h. During this state, the amplitudes of all indices change obviously, which means the degree of BPD is aggravating. This state is corresponding to state 3 in Fig. 7.

State 3 is from 160 h to the end of the test. During this state, the amplitudes of all indices increase or decrease dramatically, which means the severe bearing fault occurs. This state is corresponding to state 4 in

Fig. 7.

Fig. 8 Curve of time-domain indices over time

By comparing Fig. 7 with Fig. 8, it can be seen that time-domain indices are not sensitive to bearing incipient fault. Besides, bearing early performance degradation state cannot be separated from its normal operating state when time-domain index is adopted. Instead, bearing perfect state with no degradation and bearing early performance degradation state could be clearly distinguished when CCD is utilized. In essential, time-domain feature extraction-based analysis method uses the amplitude of index to assess the degree of BPD, while the proposed method uses CCD which has more practical significance to bearing condition monitoring. In a word, the comparison results denote that the proposed method is feasible and effective to recognize bearing incipient fault and assess the BPD process.

6 Conclusions

Reasonable and effective assessment of BPD plays an important role in predicting bearing incipient fault and reducing loss caused by bearing failure. This work proposes an assessment approach for BPD integrating extension and EEMD for the first time. This method makes full use of qualitative and quantitative evaluation features of extension, and also takes advantage of EEMD in processing non-linear and non-stationary signal. According to the analysis result of the bearing run-to-failure test, two conclusions are got as follows.

1) CCD of bearing current operating state related to its healthy operating state is adopted as the index to assess the process of BPD, which makes the evaluation result more practically significant.

2) By comparing with the results of time-domain feature extraction-based analysis method, the effectiveness of the proposed method in predicting bearing incipient fault is demonstrated. According to the proposed method, bearing incipient fault occurs in the 81st h. The results can be used to guide decision makers in making better decisions when replacing bearing, which also provides a basis for condition-based maintenance.

References

[1] ZHANG Chao, CHEN Jian-jun, XU Ya-lan. A bearing fault diagnosis method based on EMD and difference spectrum theory of singular value [J]. Journal of Vibration Engineering, 2011, 24(5): 539-545. (in Chinese)

[2] PENG Tao, YANG Hui-bin, LI Jian-bao, JIANG Hai-yan, WEI Wei. Mixed-domain feature extraction approach to rolling bearings faults based on kernek principle component analysis [J]. Journal of Central South University (Science and Technology), 2011, 42(11): 3384- 3391. (in Chinese)

[3] HU Chao, YOUN B D, WANG Ping-feng, TAEK Y Y. Ensemble of data-driven prongostic algorithms for robust prediction of remaining useful life [J]. Reliability Engineering and System Safety, 2012, 103: 120-135.

[4] TABRIZI A,GARIBALDI L, FASANA A, MARCHESIELLO S. Early damage detection of roller bearings using wavelet packet decomposition, ensemble empirical mode decomposition and support vector machine [J]. Meccanica, 2015; 50(3): 865-874.

[5] WANG Xia, LIU Cheng-wen, BI Feng-rong, BI Xiao-yang, SHAO Kang. Fault diagnosis of diesel engine based on adaptive wavelet packets and EEMD-fractal dimension [J]. Mechanical Systems and Signal Processing, 2013, 41: 581-597.

[6] WU Zhao-hua, HUANG NORDEN E. Ensemble empirical mode decomposition: A noise-assisted data analysis method [J]. Advances in Adaptive Data Analysis, 2009, 1: 1-41.

[7] ZHANG Chao, CHEN Jian-jun, GUO Xun. Gear fault diagnosis method based on ensemble empirical mode decomposition energy entropy and support vector machine [J]. Journal of Central South University (Science and Technology), 2012, 43(3): 932-939. (in Chinese)

[8] LEI Ya-guo, HE Zheng-jia, ZI Yan-yang. EEMD method and WNN for fault diagnosis of locomotive roller bearings [J]. Expert Systems with Applications, 2011, 38: 7334-7341.

[9] OZGONENEL O, YALCIN T, GUNEY I, KURT U. A new classification for power quality events in distribution systems [J]. Electric Power Systems Research, 2013, 95: 192-199.

[10] SAIDI L, BEN A J, FRIAIECH F. Application of higher order spectral features and support vector machines for bearing faults classificati- on [J]. ISA Transactions, 2015, 54: 193-206.

[11] ZAREI J, MOHAMMAD T A, HAMID K R. Vibration analysis for bearing fault detection and classification using an intelligent filter [J]. Mechatronics, 2014, 24(2): 151-157.

[12] YU Gang, LI Chang-ning, SUN Jun. Machine fault diagnosis based on Gaussian mixture model and its application [J]. International Journal of Advanced Manufacturing Technology, 2010, 48(1-4): 205-212.

[13] HE Shu-ping, XU Hui-ling. Non-fragile finite-time filter design for time-delayed Markovian jumping systems via T-S fuzzy model approach [J]. Nonlinear Dynamics, 2015, 80(3): 1159-1171.

[14] HE Shu-ping. Non-fragile passive controller design for nonlinear Markovian jumping systems via observer-based controls [J]. Neurocomputing, 2015, 147: 350-357.

[15] HUANG Run-qing, XI Li-feng, LI Xing-lin, LIU R C, QIU Hai, LEE J. Residual life predictions for ball bearings based on self-organizing map and back propagation neural network methods [J]. Mechanical Systems and Signal Processing, 2007, 21: 193-207.

[16] CAI Wen, YANG Chun-yan. Basic theory and methodology on extenics [J]. Science China, 2013, 58(13): 1190-1199. (in Chinese)

[17] CAI Wen, YANG Chun-yan, HE Bin. New development of the basic theory of extenics [J]. Engineering Science, 2003, 5(2): 80-87. (in Chinese)

[18] LIU Yu-mei, ZHAO Cong-cong, XIONG Ming-ye, XU Wen-bin, ZHANG Zhi-yuan. Application of extension theory to monitoring the running state of the high-speed railway’s gearbox [J].Transactions of Beijing Institute of Technology, 2015, 35(11): 1135-1139. (in Chinese)

[19] LIU Yu-mei, ZHAO Cong-cong, XIONG Ming-ye, ZHANG Zhi-yuan, QIAO Ning-guo. Optimization of classical domains for high-speed train transmission system [J]. Journal of Southwest Jiaotong University, 2016, 51(1): 85-90, 120. (in Chinese)

[20] HE Yong-xiu, DAI Ai-ying, ZHU Jiang, HE Hai-ying, LI Fu-rong. Risk assessment of urban network planning in china based on the matter-element model and extension analysis [J]. International Journal of Electrical Power and Energy Systems, 2011, 33(3): 775-782.

[21] HUANG Po-hsian. The extenics theory for a matching evaluation system [J]. Computers and Mathematics with Applications, 2006, 52(6, 7): 997-1010.

[22] WANG Chuan-fei, AN Gang, YANG Fan-jie. Research on fault diagnosis of certain armoured vehicle’ Gear-Box with IMF’s energy moment [J]. Advanced Materials Research, 2011, 383-390: 248-253.

[23] QIU Hai, LEE Jay, LIN Jing, YU Gang. Wavelet filter-based weak signature detection method and its application on roller bearing prognostics [J]. Journal of Sound and Vibration, 2006, 289(4, 5): 1066-1090.

(Edited by FANG Jing-hua)

Cite this article as: LIU Yu-mei, ZHAO Cong-cong, XIONG Ming-ye, ZHAO Ying-hui, QIAO Ning-guo, TIAN Guang-dong. Assessment of bearing performance degradation via extension and EEMD combined approach [J]. Journal of Central South University, 2017, 24(5): 1155-1163. DOI: 10.1007/s11771-017-3518-5.

Foundation item: Project(51575232) supported by the National Natural Science Foundation of China; Project(201215020) supported by the Natural Science Foundation of Jilin Province, China

Received date: 2015-10-10; Accepted date: 2016-04-05

Corresponding author: LIU Yu-mei, Professor, PhD; Tel: +86-431-85095506; E-mail: lymlls@163.com